
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ШКОЛА – ГИМНАЗИЯ
№10 ИМ. Э. К. ПОКРОВСКОГО» МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГОРОДСКОЙ ОКРУГ
СОГЛАСОВАНО УТВЕРЖДЕНО
Зам. директора по УВР Директор МБОУ
________________Талалаева Т.П. ________________Трещёва Н. В.
Приказ №____ от___ _____2015 г.
РАБОЧАЯ ПРОГРАММА
Кулькова Людмила Михайловна учитель математики высшей квалификационной категории алгебра базовый уровень
10 класс
РАССМОТРЕНО
на заседании ШМО
председатель
____________Кулькова Л.М.
Протокол №_______________
От «___» ____________ 2015 г.
Симферополь 2015-2016
Рабочая программа по математике для 10 класса разработана и составлена в соответствии с федеральным компонентом государственного стандарта начального общего, основного общего и среднего (полного) общего образования. (Приказ МО РФ от 05.03.2004 №1089).
Рабочая программа разработана на основе:
Ø примерной программы общеобразовательных учреждений. Алгебра и начала математического анализа 10-11 кл./ Составитель: Т. А. Бурмистрова - М.: Просвещение, 2009;
Ø примерной программы общеобразовательных учреждений. Геометрия 10-11 классы. Составитель Т. А. Бурмистрова - М.: Просвещение, 2010;
Ø федерального базисного плана для образовательных учреждений РФ, реализующих программы общего
образования. (Приказ МО РФ от 09. 03. 2004г №1312) (с изменениями в редакции приказа от 20.08. 2008 № 241);
Для реализации программного содержания используется следующие учебники:
1. Алимов Ш А, Колягин Ю М и др. Алгебра и начала анализа : Учебник для 10-11 кл. общеобразовательных
учреждений/ М.: Просвещение, 2010.
Общая характеристика учебного предмета
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия (стереометрия)», «Элементы комбинаторики, теории вероятностей, статистики и логики», вводится линия «Начала математического анализа». В рамках указанных содержательных линий решаются следующие задачи:
систематизация сведений о числах; изучение новых видов числовых выражений и формул; совершенствование практических навыков и вычислительной культуры, расширение и совершенствование алгебраического аппарата, сформированного в основной школе, и его применение к решению математических и нематематических задач; расширение и систематизация общих сведений о функциях, пополнение класса изучаемых функций, иллюстрация
широты применения функций для описания и изучения реальных зависимостей; развитие представлений о вероятностно-статистических закономерностях в окружающем мире, совершенствование
интеллектуальных и речевых умений путем обогащения математического языка, развития логического мышления; знакомство с основными идеями и методами математического анализа.
Цели
Изучение математики в старшей школе на базовом уровне направлено на достижение следующих целей:
• формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;
• развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для обучения в высшей школе по соответствующей специальности, в будущей профессиональной деятельности;
• овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;
• воспитание средствами математики культуры личности: отношения к математике как части общечеловеческой культуры: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Общеучебные умения, навыки и способы деятельности
В ходе освоения содержания математического образования учащиеся овладевают разнообразными способами деятельности, приобретают и совершенствуют опыт:
• построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин;
• выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; выполнения расчетов практического характера; использования математических формул и самостоятельного составления формул на основе обобщения частных случаев и эксперимента;
• самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
• проведения доказательных рассуждений, логического обоснования выводов, различения доказанных и недоказанных утверждений, аргументированных и эмоционально убедительных суждений;
• самостоятельной и коллективной деятельности, включения своих результатов в результаты работы группы, соотнесение своего мнения с мнением других участников учебного коллектива и мнением авторитетных источников.
Тематическое планирование
|
№ |
Содержание учебного материала |
Кол-во часов |
|
|
1. |
Действительные числа (6 часов)
|
6+3 |
9 |
|
2. |
Степенная функция (7 часов)
|
7+3 |
10 |
|
3 П |
Показательная функция (9 часа)
|
9+4 |
13 |
|
4. |
. Логарифмическая функция (14часов)
|
14+5 |
19 |
|
5 |
Тригонометрические формулы (15час) |
15+3 |
18 |
|
6 V |
. Тригонометрические уравнения (10 часов)
|
10+5 |
15 |
|
7 |
Повторение и решение задач (7 часов)
|
7+3 |
10 |
|
8 |
Резерв |
8 |
8 |
|
9 |
Всего |
102 |
102 |
ОСНОВНОЕ СОДЕРЖАНИЕ
АЛГЕБРА
Глава I. Действительные числа (9 часа)
Целые и рациональные числа. Действительные числа. Бесконечно убывающая геометрическая прогрессия.
Арифметический корень натуральной степени. Степень с рациональным и действительным показателями. Контрольная работа № 1 по теме: «Действительные числа».
Входная контрольная работа.
Знать:
Ÿ понятие натурального числа;
Ÿ понятие целого числа;
Ÿ понятие действительного числа;
Ÿ понятие модуля числа;
Ÿ понятие арифметического корня n –й степени и его свойства; Ÿ свойства степени с действительным показателем.
Уметь:
Ÿ уметь находить сумму бесконечно убывающей геометрической прогрессии;
Ÿ обращать бесконечно периодическую дробь в обыкновенную;
Ÿ уметь выполнять преобразования выражений, содержащих арифметические корни.
Глава II. Степенная функция (10 часов)
Степенная функция, еѐ свойства и график. Взаимно обратные функции. Равносильные уравнения и неравенства. Иррациональные уравнения. Иррациональные неравенства. Контрольная работа № 2 по теме: «Степенная функция» Знать:
Ÿ свойства степенной функции во всех еѐ разновидностях;
Ÿ определение и свойства взаимно обратных функций;
Ÿ определения равносильных уравнений и уравнения-следствия;
Ÿ понимать причину появления посторонних корней и потери корней;
Ÿ что при возведении в натуральную степень обеих частей уравнения получается уравнение – следствие; Ÿ при решении неравенства можно выполнять только равносильные преобразования;
Ÿ что следует избегать деления обеих частей уравнения(неравенства) на выражение с неизвестным. Уметь:
∙ схематически строить график степенной функции в зависимости от принадлежности показателя степени;
Ÿ перечислять свойства;
Ÿ выполнять преобразования уравнений, приводящие к уравнениям-следствиям; Ÿ решать иррациональные уравнения и неравенства. Глава III. Показательная функция (13часа)
Показательная функция, еѐ свойства и график. Показательные уравнения. Показательные неравенства. Системы показательных уравнений и неравенств.
Контрольная работа № 3 по теме: «Показательная функция».
Знать:
Ÿ определение и свойства показательной функции;
Ÿ способы решения показательных уравнений.
Уметь:
Ÿ уметь строить график показательной функции в зависимости от значения основания а; Ÿ описывать по графику свойства;
Ÿ применять знания о свойствах показательной функции к решению прикладных задач;
Ÿ решать уравнения, используя тождественные преобразования на основе свойств степени, с помощью разложения на множители выражений, содержащих степени, применяя способ замены неизвестной степени новым неизвестным;
Ÿ решать показательные неравенства на основе свойств монотонности показательной функции; Ÿ решать системы показательных уравнений и неравенств.
Глава IV. Логарифмическая функция (19часов)
Логарифмы. Свойства логарифмов. Десятичные и натуральные логарифмы. Логарифмическая функция, еѐ свойства и график. Логарифмические уравнения. Логарифмические неравенства.
Контрольная работа за 1 полугодие.
Контрольная работа №4 по теме: «Логарифмическая функция»
Знать:
Ÿ понятие логарифма числа и основное логарифмическое тождество;
Ÿ основные свойства логарифмов;
Ÿ понятие десятичного и натурального логарифмов;
Ÿ определение логарифмической функции;
Ÿ свойства логарифмической функции и еѐ график.
Уметь:
Ÿ применять свойства логарифмов для преобразований логарифмических выражений;
Ÿ применять формулу перехода от логарифма по одному основанию к логарифму по другому основанию; Ÿ применять свойства логарифмической функции при сравнении значений выражений и решении простейших логарифмических уравнений и неравенств;
Ÿ решать различные логарифмические уравнения и их системы с использованием свойств логарифмов и общих методов решения уравнений;
Ÿ решать логарифмические неравенства на основании свойств логарифмической функции. Глава V. Тригонометрические формулы (18часов)
Радианная мера угла. Поворот точки вокруг начала координат. Определение синуса, косинуса и тангенса угла. Знаки синуса, косинуса и тангенса. Зависимость между синусом, косинусом и тангенсом одного и того же угла. Тригонометрические тождества. Синус, косинус и тангенс углов α и - α. Формулы сложения. Синус, косинус и тангенс двойного угла. Синус, косинус и тангенс половинного угла. Формулы приведения. Сумма и разность синусов. Сумма и разность косинусов
Контрольная работа № 5 по теме: «Тригонометрические формулы».
Знать:
Ÿ определения синуса, косинуса и тангенса;
Ÿ основные формулы, выражающие зависимость между синусом, косинусом и тангенсом Ÿ определение радиана;
Ÿ понятие тождества как равенства; Уметь:
Ÿ переводить радианную меру угла в градусы и обратно;
Ÿ поворачивать начальную точку единичной окружности вокруг начала координат на угол α и находить положение точки окружности, соответствующей данному действительному числу;
Ÿ находить синус, косинус тангенс для чисел вида Π/2k, k €; Z
Ÿ применять формулы для вычисления значений синуса, косинуса и тангенса числа по заданному значению одного из них;
Ÿ доказывать тождества с использованием изученных формул;
Ÿ выполнять преобразование тригонометрических выражений
Глава VI . Тригонометрические уравнения (15 часов)
Уравнение cosx=a. Уравнение sinx =a. Уравнение tgx =a. Решение тригонометрических уравнений .Примеры решения простейших тригонометрических неравенств.
Контрольная работа № 6 по теме: «Тригонометрические уравнения».
Знать:
Ÿ понятия арккосинуса, арксинуса и арктангенса;
Ÿ формулы корней простейших тригонометрических уравнений;
Ÿ приѐмы решений различных типов уравнений;
Ÿ приемы решения простейших тригонометрических неравенств.
Уметь:
Ÿ решать простейшие тригонометрические уравнения;
Ÿ применять различные приѐмы при решении тригонометрических уравнений; Ÿ решать простейшие тригонометрические неравенства.
Повторение и решение задач (10 часов)
Резерв 8 часов
Итоговая контрольная работа.
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ
В результате изучения математики на базовом уровне ученик должен
знать/понимать
• значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
• значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
• универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
• вероятностный характер различных процессов окружающего мира;
АЛГЕБРА уметь
• выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
• проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
• вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
• практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики уметь
• определять значение функции по значению аргумента при различных способах задания функции; строить графики изученных функций;
• описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
• решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
• использовать приобретенные знания и умения в практической деятельности и повседневной жизни для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
Начала математического анализа уметь
• вычислять производные и первообразные элементарных функций, используя справочные материалы;
• исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
• вычислять в простейших случаях площади с использованием первообразной;
• использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;
Уравнения и неравенства уметь
• решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
• составлять уравнения и неравенства по условию задачи;
• использовать для приближенного решения уравнений и неравенств графический метод;
• изображать на координатной плоскости множества решений простейших уравнений и их систем; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для построения и исследования простейших математических моделей;
Элементы комбинаторики, статистики и теории вероятностей уметь
• решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
• вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: анализа реальных числовых данных, представленных в виде диаграмм, графиков; анализа информации статистического характера.
• КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
|
№ п/п |
Номер в теме |
Наименование раздела и тем |
Кол. час. |
Дата проведения |
Примечания |
|
|
По плану |
фактически |
|
||||
|
|
|
|
Гл. I Действительные числа (9 ч.) |
|||
|
1. |
1 |
Целые и рациональные числа.
|
1 |
1.09-4.09 |
|
|
|
2. |
2 |
Прогрессия |
1 |
1.09-4.09 |
|
|
|
3. |
3 |
Прогрессия |
1 |
1.09-4.09 |
|
|
|
4. |
4 |
Степень с рациональным и действительным показателем |
1 |
7.09-11.09 |
|
|
|
5. |
5 |
Степень с рациональным и действительным показателем |
1 |
7.09-11.09 |
|
|
|
6. |
6 |
Степень с рациональным и действительным показателем |
1 |
7.09-11.09 |
|
|
|
7. |
7 |
Степень с рациональным и действительным показателем |
1 |
14.09-18.09 |
|
|
|
8. |
8 |
Степень с рациональным и действительным показателем |
1 |
14.09-18.09 |
|
|
|||
|
9. |
9 |
Контрольная работа №1.1 |
1 |
14.09-18.09 |
|
|
|||
|
|
|
Гл. II Степенная функция (10ч.) |
|||||||
|
10. |
|
1 |
. Степенная функция, ее свойства и график |
1 |
21.09-25.09 |
|
|
||
|
11. |
|
2 |
. Степенная функция, ее свойства и график |
1 |
14.09-18.09 |
|
|
||
|
12. |
|
3 |
. Степенная функция, ее свойства и график |
1 |
21.09-25.09 |
|
|
||
|
13. |
|
4 |
. Равносильные уравнения и неравенства |
1 |
28.09-2.10 |
|
|
||
|
14. |
|
5 |
. Равносильные уравнения и неравенства |
1 |
28.09-2.10 |
|
|
||
|
15. |
|
6 |
. Равносильные уравнения и неравенства |
1 |
28.09-2.10 |
|
|
||
|
16. |
|
7 |
. Иррациональные уравнения |
1 |
5.10-9.10 |
|
|
||
|
17. |
|
8 |
. Иррациональные уравнения |
1 |
5.10-9.10 |
|
|
||
|
18. |
|
9 |
. Иррациональные уравнения |
1 |
5.10-9.10 |
|
|
||
|
19. |
10 |
|
Контрольная работа №.2 |
1 |
12.10-16.10 |
|
|
||
|
|
Гл.III Показательная функция(13 ч.) |
||||||||
|
20. |
1 |
|
Показательная функция, ее свойства и график |
1 |
12.10-16.10 |
|
|
||
|
21. |
|
2 |
Показательная функция, ее свойства и график |
|
1 |
12.10-16.10 |
|
|
|
22. |
|
3 |
Показательные уравнения |
|
1 |
19.10-23.10 |
|
|
|
23. |
|
4 |
Показательные уравнения |
|
1 |
19.10-23.10 |
|
|
|
24. |
|
5 |
Показательные уравнения |
|
1 |
19.10-23.10 |
|
|
|
25. |
|
6 |
Показательные уравнения |
|
1 |
28.10-30.10 |
|
|
|
26. |
|
7 |
Показательные неравенства |
|
1 |
28.10-30.10 |
|
|
|
27. |
|
8 |
Показательные неравенства |
|
1 |
28.10-30.10 |
|
|
|
28. |
|
9 |
Показательные неравенства |
|
1 |
9.11-13.11 |
|
|
|
29. |
|
10 |
Показательные неравенства |
|
1 |
9.11-13.11 |
|
|
|
30. |
|
11 |
Системы показательных уравнений и неравенств |
|
1 |
9.11-13.11 |
|
|
|
31. |
|
12 |
Системы показательных уравнений и неравенств |
|
1 |
16.11-20.11 |
|
|
|
32. |
|
13 |
Контрольная работа №.3 |
|
1 |
16.11-20.11 |
|
|
|
|
|
Гл. IV Логарифмическая функция (19 ч.) |
||||||
|
33. |
1. |
Логарифмы |
|
1 |
16.11-20.11 |
|
|
|
|
34. |
2. |
Логарифмы |
|
1 |
23.11-27.11 |
|
|
|
|
35. |
3. |
Свойства логарифмов |
|
1 |
23.11-27.11 |
|
|
|
|
36. |
4. |
Свойства логарифмов |
1 |
23.11-27.11 |
|
|
|
37. |
5. |
Свойства логарифмов |
1 |
30.11-4.12 |
|
|
|
38. |
6. |
Десятичные и натуральные логарифмы |
1 |
30.11-4.12 |
|
|
|
39. |
7. |
Десятичные и натуральные логарифмы |
1 |
30.11-4.12 |
|
|
|
40. |
8. |
Десятичные и натуральные логарифмы |
1 |
7.12-11.12 |
|
|
|
41. |
9. |
Логарифмическая функция, ее свойства и график |
1 |
7.12-11.12 |
|
|
|
42. |
10. |
Логарифмическая функция, ее свойства и график |
1 |
7.12-11.12 |
|
|
|
43. |
11. |
Логарифмические уравнения |
1 |
14.12-18.12 |
|
|
|
44. |
12. |
Логарифмические уравнения |
1 |
14.12-18.12 |
|
|
|
45. |
13. |
Логарифмические уравнения |
1 |
14.12-18.12 |
|
|
|
46. |
14. |
Логарифмические уравнения |
1 |
14.12-18.12 |
|
|
|
47. |
15. |
Логарифмические неравенства |
1 |
21.12-25.12 |
|
|
|
48. |
16. |
Логарифмические неравенства |
1 |
28.12-30.12 |
|
|
|
49. |
17. |
Логарифмические неравенства |
1 |
28.12-30.12 |
|
|
|
50. |
18. |
Урок обобщения и систематизации знаний |
1 |
28.12-30.12 |
|
|
|
51. |
19. |
Контрольная работа №.4 |
1 |
11.01-16.01 |
|
|
|
||
|
|
V. Тригонометрические формулы (18часов) |
||||||||
|
52. |
1. |
1Радианная мера угла |
1 |
11.01-16.01 |
|
|
|||
|
53. |
2. |
2Поворот точки вокруг начала координат |
1 |
28.12-30.12 |
|
|
|||
|
54. |
3. |
3Определение синуса, косинуса и тангенса угла |
1 |
18.01-23.01 |
18.01-23.01 |
|
|||
|
55. |
4. |
4Знаки синуса, косинуса и тангенса |
1 |
18.01-23.01 |
18.01-23.01 |
|
|||
|
56. |
5. |
5Зависимость между синусом, косинусом и тангенсом одного и того же угла. |
1 |
18.01-23.01 |
18.01-23.01 |
|
|||
|
57. |
6. |
6Тригонометрические тождества |
1 |
25.01-30.01 |
25.01-30.01 |
|
|||
|
58. |
7. |
Тригонометрические тождества |
1 |
25.01-30.01 |
|
|
|||
|
59. |
8. |
7Тригонометрические тождества |
1 |
25.01-30.01 |
|
|
|||
|
60. |
9. |
8Синус, косинус и тангенс углов и - |
1 |
1.02-6.02 |
|
|
|||
|
61. |
10. |
9Формулы сложения |
1 |
1.02-6.02 |
|
|
|||
|
62. |
11. |
Формулы сложения |
1 |
1.02-6.02 |
|
|
|||
|
63. |
12. |
1Формулы сложения 0 |
1 |
8.02-13.02 |
|
|
|||
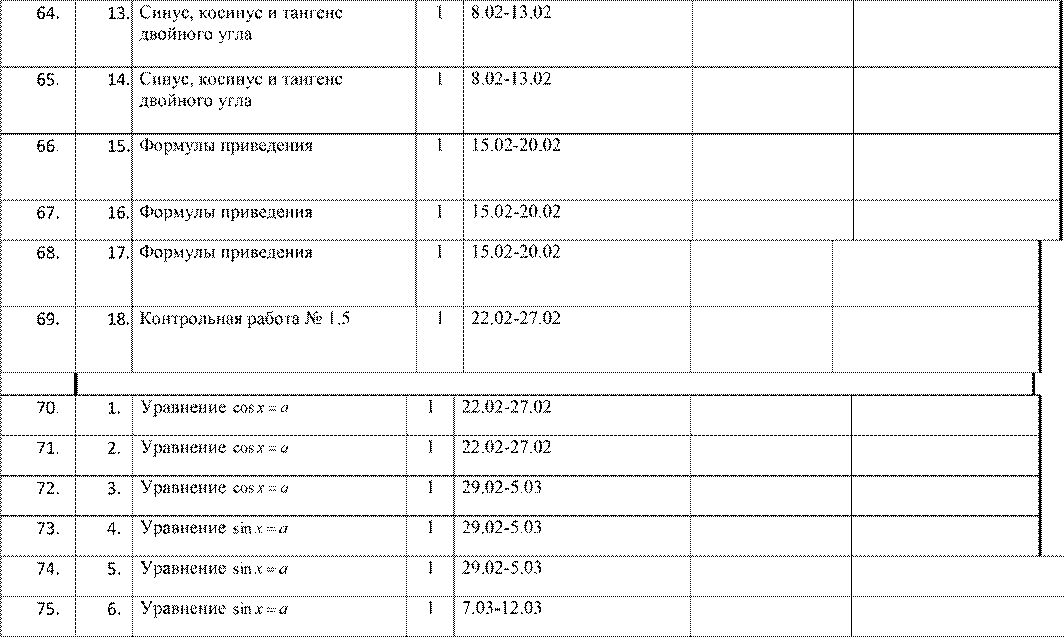 |
|
76. |
7. |
Уравнение tgxa |
1 |
7.03-12.03 |
|
|
|
|
77. |
8. |
Уравнение tgxa |
1 |
7.03-12.03 |
|
|
|
|
78. |
9. |
Решение тригонометрических уравнений |
1 |
14.03-17.03 |
|
|
|
|
79. |
10. |
Решение тригонометрических уравнений |
1 |
14.03-17.03 |
|
|
|
|
80. |
11. |
Решение тригонометрических уравнений |
1 |
14.03-17.03 |
|
|
|
|
81. |
12. |
Решение тригонометрических уравнений |
1 |
28.03-2.04 |
|
|
|
|
82. |
13. |
Решение тригонометрических уравнений |
1 |
28.03-2.04 |
|
|
|
|
83. |
14. |
Решение тригонометрических уравнений |
1 |
28.03-2.04 |
|
|
|
|
84. |
15. |
Контрольная работа № 1.6 |
1 |
4.04-9.04 |
|
|
|
|
|
|
|
|||||
|
85. |
1. |
Повторение. Иррациональные уравнения |
1 |
4.04-9.04 |
|
|
|
|
86. |
2. |
Повторение. Показательные уравнения. |
1 |
11.04-16.04 |
|
|
|
|
87. |
3. |
Повторение. Показательные уравнения. |
1 |
11.04-16.04 |
|
|
|
|
88. |
4. |
Повторение. Показательные уравнения. |
1 |
11.04-16.04 |
|
|
|
|
89. |
5. |
Повторение. Показательные уравнения. |
1 |
28.03-2.04 |
|
|
|
|
90. |
6. |
Повторение. Логарифмические уравнения |
1 |
18.04-23.04 |
|
|
|
91. |
7. |
Повторение. Тригонометрические преобразования. |
1 |
18.04-23.04 |
|
|
|
92. |
8. |
Повторение. Тригонометрические преобразования. |
1 |
18.04-23.04 |
|
|
|
93. |
9. |
Повторение. Показательные уравнения. |
1 |
25.04-30.04 |
|
|
|
94. |
10. |
Повторение. Показательные уравнения. |
1 |
2.05-7.05 |
|
|
|
95. |
2Итого: контрольных работ 6 |
|
|
|||
|
96. |
Резерв 6 часов |
|
|
|||
|
97. |
Всего 102 часа |
|
|
|||
1. Программы общеобразовательных учреждений. Алгебра и начала математического анализа. 10-11 классы. /Сост. Т.А.Бурмистрова – М.: «Просвещение», 2014 г.
2. Программы общеобразовательных учреждений. Математика. /Т.А.Бурмистрова - М.: «Просвещение», 1996г.
3. Алгебра и начала анализа: учеб. для 10 – 11 кл. /Ш.А.Алимов, Ю.М.Колягин, и др.; - 12-еизд.. – М.: «Просвещение», 2014.
4. Контрольные и проверочные работы по алгебре 10 – 11 кл.: метод. пособие / Л.И.Звавич, Л.Я.Шляпочник. – М.: «Дрофа», 2014.
5. Дидактические материалы по алгебре и началам анализа для 10 класса общеобразовательных учреждений/ М.И. Шабунин, М.В.Ткачѐва, Н.Е. Фѐдорова, Р.Г.Газарян. – 2-е изд. – М.: «Просвещение», 20014.
6. Сборник тренировочных тестовых заданий по математике для подготовки к итоговой аттестации, в том числе и по материалам ЕГЭ, для учащихся 11-х классов: методическое пособие / авт.-сост. Л.С.Яковлева. – Самара: ООО «Офорт», 2014.
7. Ш.А.Алимов, Ю.М.Колягин, Ю.В.Сидоров, Н.Е.Фѐдоров, М,И.Шабунин.Алгебра и начала математического анализа. Москва. Просвещение, 2014.
8. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия, 10–11: Учебник для общеобразовательных учреждений/ – М.: Просвещение, 2014.
9. Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 10 кл. – М.: Просвещение, 2014.
10. Научно-теоретический и методический журнал «Математика в школе»
11. Еженедельное учебно-методическое приложение к газете «Первое сентября» Математика
12. Ковалева Г.И, Мазурова Н.И. геометрия. 10-11 классы: тесты для текущего и обобщающего контроля. – Волгоград: Учитель, 2014.
13. Единый государственный экзамен 2014-2015. математика. Учебно-тренировочные материалы для подготовки учащихся / ФИПИ-М.: Интеллект-Центр, 2005-2011.
14. http://school-collection.edu.ru/ – единая коллекция цифровых образовательных ресурсов.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.