

Составитель Швырева Н.А.
Рабочая тетрадь по геометрии для студентов 1 курса на базе основного общего образования. БОУ ОО СПО «Омавиат», 2013 г.
Рабочая тетрадь предназначена для организации обучения и контроля по разделу «Многогранники» как на уровне стандарта математического образования, так и на более высоком уровне. Содержит задания для закрепления, повторения, обобщения изученного материала. Решения выполняются непосредственно в рабочей тетради, что, кроме всего прочего, экономит время студента, избавляя его от выполнения механической работы по перечерчиванию условий задач.
Предлагаемая система заданий позволяет быстро и оперативно получать информацию об усвоении учебного материала студентами.
Данное пособие по геометрии направлено на формирование у студентов основных математических умений, пространственного мышления и развитие самостоятельного познания. Предлагаемые задания соответствуют стандарту математического образования и дают возможность преподавателю организовывать работу учащихся на уроках и дома.
Пособие включает обучающие и проверочные задания по учебной дисциплине естественно - научного цикла: «Математика» по теме «Многогранники», с использованием методов таксономии Б.Блума. Задания расположены по степени усложнения характера познавательной деятельности: знание, понимание, применение, анализ, синтез, оценка.
Предложенные задания в учебном пособии различные по форме и содержанию. Первая группа заданий, проверяющих знание формулировок, конкретных фактов, основных понятий. Эти задания предлагают вставить пропущенные слова в утверждения, чтобы оно было верным, закончить формулировку определения или ответить на вопросы. Вторая группа заданий проверяет понимание смысла определений, теорем, свойств, признаков. В заданиях такого рода необходимо объяснить факты, правила, принципы, ответить на вопросы, уточняющие некоторые детали, тонкости в содержании геометрического факта. Также преобразовать словесный материал в графическую форму. Третья группа направлена на практическое применение теории в конкретных ситуациях, а также формирует у учащихся умение подвести условие задания под некоторое геометрическое понятие или факт, использовать свойства и признаки в новых ситуациях. Многие из этих заданий способствуют дальнейшему развитию пространственного мышления учащихся.
В четвертой группе заданий предусмотрен анализ решения выборочных задач, заполнение пропусков в частично решенных задачах. Данные задания обучают учащихся вычленять части целого, выявлять взаимосвязь между ними, видеть ошибки и упущения в логике рассуждений, проводить различие между фактами и следствиями.
Пятая группа заданий обозначает умение комбинировать элементы, чтобы получить целое, обладающее новизной. В заданиях такого рода необходимо составить условие задач, предварительно составить план решения или графическое изображение фигур.
Последняя группа заданий обозначает умение оценивать значение того или иного материала. Это задания с выбором ответа и с данным ответом, что позволяет осуществить учащимися самоконтроль за качеством своего обучения.
Предложенные задания могут быть использованы преподавателями на занятиях в ходе закрепления, повторения, обобщения изученного материала по теме, а также учащимися в самостоятельной работе, для самопроверки и самоконтроля.
§1. Понятие многогранника. Призма
1.1.Теоретические сведения……………………………………………………………………6
1.2.Упражнения…………………………………………………………………………………9
1.3.Практические решения задач……………………………………………………………...14
1.4.Задачи для самостоятельного решения…………………………………………………..19
§2. Пирамида. Усеченная пирамида
1.1.Теоретические сведения……………………………………………………………………19
1.2.Упражнения…………………………………………………………………………………21
1.3.Практические решения задач……………………………………………………...............27
1.4.Задачи для самостоятельного решения…………………………………………………...31
§3. Правильные многогранники
3.1.Теоретические сведения……………………………………………………………………31
3.2.Упражнения………………………………………………………………………………....37
Список литературы……………………………………………………………………………..39
§1. Понятие многогранника. Призма
Замкнутая поверхность, составленная из многоугольников, и ограниченное ею некоторое геометрическое тело, называется многогранником. Многогранниками являются тетраэдр, параллелепипед.
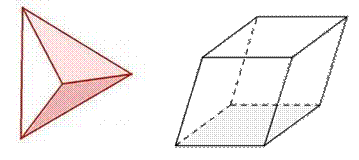
Тетраэдр Параллелепипед
Многоугольники, из которых составлена поверхность многогранника, называются его гранями.
Стороны граней называются ребрами, а концы ребер – вершинами многогранника.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.
Многогранник обычно обозначается перечислением его вершин.
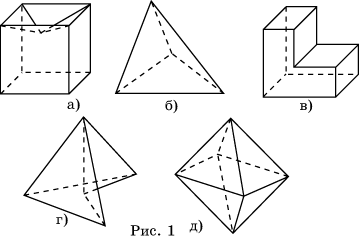
Многогранники бывают выпуклые и невыпуклые. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
На рисунке 1, б и в изображены выпуклые многогранники, а, г и д – невыпуклые многогранники.
Свойства выпуклых многогранников
Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.
Свойство 2. В выпуклом многограннике сумма всех плоских углов при каждой его вершине меньше 3600.
Свойство 3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.
Теорема Эйлера. Для любого выпуклого многогранника имеет место равенство
В - Р + Г = 2,
где В - число вершин, Р - число ребер и Г - число граней данного многогранника.
Свойство 4. В любом выпуклом многограннике найдется грань с числом ребер меньшим или равным пяти.
Обозначения:
V — объем;
Sполн — площадь полной поверхности;
Sбок — площадь боковой поверхности;
Sо — площадь основания;
Pо — периметр основания;
Pо — периметр перпендикулярного сечения; l — длина ребра; h — высота.
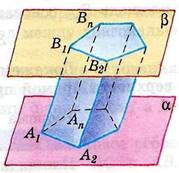
Многогранник, составленный из двух равных многоугольников А1 А2…Аn и В1 В2…Вn (рис. 2), расположенных в параллельных плоскостях и n параллелограммов, называется призмой.
Элементы призмы:
1.
 Параллелограммы A1B1B2A2,
A2B2B3A3, и т. д. называются боковыми
гранями призмы.
Параллелограммы A1B1B2A2,
A2B2B3A3, и т. д. называются боковыми
гранями призмы.
2. Многоугольники A1A2A3…An, В1В2В3…Вn, называются основаниями.
3. Отрезки A1B1, …АnBn называются боковыми ребрами
призмы.
4. Перпендикуляр, проведенный из какой-нибудь точки одного
основания к плоскости другого основания, называется его высотой. Рис. 2
5. Отрезок, соединяющий две вершины не принадлежащие одной грани называется диагональю.
Свойства призмы:
1. Основания призмы являются равными многоугольниками.
2. Боковые грани призмы являются параллелограммами.
3. Боковые ребра призмы равны.
4. Противоположные ребра параллельны и равны.
5. Все боковые ребра равны и параллельны.
6. Противоположные боковые грани равны и параллельны.
7. Высота перпендикулярна каждому основанию.
8. Диагонали пересекаются в одной точке и делятся в ней пополам.
9. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
S = P · h бок осн
P - периметр h – высота призмы
10. Площадь полной поверхности призмы называется сумма площадей всех ее граней.
S S + 2S .
пол = бок осн
11.Объем призмы равен произведению площади основания на высоту.
|
а) По виду оснований. |
Виды призмы |


|
треугольная
|
четырехугольная |
шестиугольная |
б) По расположению боковых ребер к основанию.
|
Прямая призма Прямой называют такую призму, боковые ребра которой перпендикулярны к основаниям.
|
Наклонная призма Наклонной называют такую призму, боковые ребра которой не будут перпендикулярны к основаниям. |


|
Свойства 1. Боковые грани-прямоугольники. 2.Высота равна с боковому ребру. 3. Sбок = Росн∙ Н, Росн- периметр основания призмы, Н- боковое ребро. 4. Sпол= Sбок+2Sосн 5. V= Sосн∙Н |
Свойства 1. Боковые грани-параллелограммы. 2.Высоты не совпадают с боковыми ребрами. 3. Sбок = Рперпенд. сеч∙ L, Рперпенд. сеч - периметр перпендикулярного сечения призмы, L- боковое ребро. 4. Sпол= Sбок+2Sосн |
5. V= Sосн∙Н
в) Правильные призмы это прямые призмы в основании которых лежит правильный многоугольник.
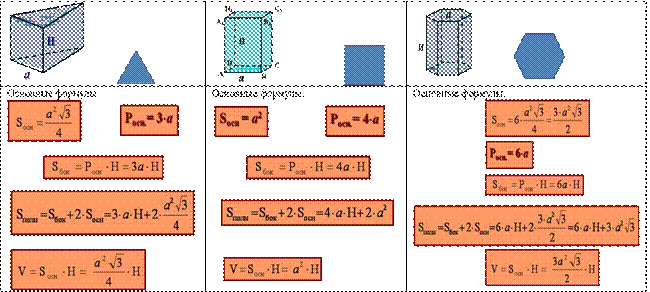
г) Параллелепипеды. Параллелепипед это призма, в основании которой лежит параллелограмм.
Наклонный параллелепипед. Прямой параллелепипед.
1. Среди изображенных тел выберите номера тех, которые являются многогранниками и закончите предложение.
|
|
|
|
|
1 |
2 |
3 |
Многогранник - это геометрическое тело, поверхность которого состоит _________
__________________________________________________________________________
__________________________________________________________________________ 2. Заполните таблицу
1 2

|
Элементы многогранника |
|
Колич |
ество |
|
1 |
|
2 |
|
|
Вершины |
|
|
|
|
Грани |
|
|
|
|
Ребра |
|
|
|
3. Выполните чертеж выпуклого многогранника и закончите предложение.
 Многогранник называется выпуклым,
Многогранник называется выпуклым,
если он расположен__________________
___________________________________
___________________________________
4. Выполните чертеж наклонной четырехугольной призмы, обозначьте ее и запишите:
Призма _____________________
Вершины _____________________
Основания _____________________
Боковые ребра ____________________
 Боковые грани ____________________ _________________________________
Противоположные грани __________
Боковые грани ____________________ _________________________________
Противоположные грани __________
_________________________________
_
5. Закончите предложения.
1. Призмой называется многогранник, составленный_____________________________
__________________________________________________________________________
__________________________________________________________________________
2. Высотой призмы называется _______________________________________________ __________________________________________________________________________
3. Диагональю призмы называется ____________________________________________ __________________________________________________________________________
4. Призма называется наклонной, если _________________________________________
__________________________________________________________________________
5. Призма называется прямой, если ____________________________________________ __________________________________________________________________________
6. Призма называется правильной, если ________________________________________
__________________________________________________________________________
7. Боковой поверхностью призмы называется ___________________________________ __________________________________________________________________________
8. Параллелепипедом называется _____________________________________________
__________________________________________________________________________
__________________________________________________________________________
9. Прямоугольным параллелепипедом называется _______________________________ __________________________________________________________________________
10. Кубом называется _______________________________________________________
__________________________________________________________________________
__________________________________________________________________________ 11. Примеры моделей призмы и параллелепипеда из вашей профессии ______________
__________________________________________________________________________ __________________________________________________________________________
6. Выполните задания.
1. Среди изображенных тел выберите номера тех, которые являются призмами.

1 2 3 4 5 6 7 8
Ответ: ____________________________________________________________________
2. Среди изображенных тел выберите номера тех, которые являются параллелепипедами.
1 2 3 4 5 6 7 8
Ответ: ____________________________________________________________________
3. Начертите прямую четырехугольную призму. Обозначьте:

4. В прямоугольном параллелепипеде ABCDA1B1C1D1постройте сечение, проходящее через вершины А; В1; С.
____________________________

 ____________________________11
____________________________11
____________________________
____________________________
____________________________
5.Проведите сечение треугольной наклонной призмы, проходящее через середины боковых ребер. Как расположено это сечение по отношению к плоскости основания? Какая фигура получиться в сечении?
 Поясните свои
рассуждения
Поясните свои
рассуждения
____________________________
____________________________
____________________________
 ____________________________
____________________________ ____________________________
____________________________
____________________________ ____________________________
7. Ответьте на вопросы.
1. Какие многоугольники лежат в основаниях призмы? ___________________________ __________________________________________________________________________ 2. Какими отрезками являются боковые ребра призмы? ___________________________
__________________________________________________________________________ 3. Какими фигурами являются боковые грани призмы? __________________________ __________________________________________________________________________
4. Что представляет собой диагональное сечение призмы? ________________________ __________________________________________________________________________
5. Какими фигурами являются все грани параллелепипеда? _______________________ __________________________________________________________________________
6. Какими фигурами являются все грани прямоугольного параллелепипеда? _________ __________________________________________________________________________
7. Сколько измерений у прямоугольного параллелепипеда? _______________________ __________________________________________________________________________
8. Что является высотой прямой призмы? ______________________________________ __________________________________________________________________________ 9. Какие многоугольники являются основанием и боковой гранью пятиугольной призмы? __________________________________________________________________ __________________________________________________________________________
10. Призма имеет 30 граней. Какой многоугольник лежит в ее основании? ___________ __________________________________________________________________________ 11. Будет ли сечение, перпендикулярное боковому ребру призмы, перпендикулярно к ее боковой грани? Ответ обоснуйте __________________________________________ __________________________________________________________________________
__________________________________________________________________________
12. В какой призме боковые ребра параллельны ее высоте? _______________________ __________________________________________________________________________ 13. Если все ребра призмы равны, то будет ли она правильной? Ответ обоснуйте____
__________________________________________________________________________
__________________________________________________________________________
14. Существует ли призма, у которой только одна баковая грань перпендикулярна основанию? Ответ обоснуйте _______________________________________________ __________________________________________________________________________
__________________________________________________________________________
8. Выполните задания.
1. Начертите прямую призму, в основании которой лежит прямоугольник
2. Напишите название грани, которая является нижним основанием призмы
3. Напишите одну пару параллельных ребер
4. Сколько в данной призме пар взаимно перпендикулярных ребер?
5. Выделите на чертеже штриховкой одну пару параллельных граней
6. Запишите отрезок, который является высотой призмы
7. Запишите одну пару равных граней призмы
8. Начертите диагональ призмы
9. Вычислите площадь полной поверхности призмы, если стороны основания призмы равны 5 и 7 см., а боковое ребро – 9 см.
10. Вычислите объем призмы
|
|
Решение:
 2.
_______________________________ 3. _______________________________ 4.
_______________________________
2.
_______________________________ 3. _______________________________ 4.
_______________________________
6. _______________________________ 7. _______________________________
9. _______________________________
________________________________
________________________________
10. ________________________________ ______________________________
9. Докажите.
Докажите, что площадь боковой поверхности призмы вычисляется по формуле S = P*h ,где Р – периметр основания, h–высота призмы
 Доказательство:
_________________
Доказательство:
_________________
____________________________
____________________________
____________________________
____________________________
____________________________
____________________________
 ____________________________
____________________________
10. Заполните пропуски, чтобы утверждение было верным. 1. В выпуклом многограннике сумма всех плоских углов при каждой его вершине ________________3600.
2. У параллепипеда противоположные грани __________________ и ______________
3. Диагонали параллелепипеда пересекаются ___________________________________
__________ и ____________________________________________________________
4. В прямоугольном параллелепипеде квадрат любой диагонали равен _____________ __________________________________________________________________________
5. Площадью полной поверхности призмы называется сумма _____________________
__________________________________________________________________________
__________________________________________________________________________
6. Площадью боковой поверхности призмы называется ___________________________ __________________________________________________________________________
7. Площадь боковой поверхности прямой призмы равна произведению _____________
__________________________________________________________________________
__________________________________________________________________________
8. Все двугранные углы при боковых гранях прямой призмы ______________________ __________________________________________________________________________ 9. Правильная четырехугольная призма, высота которой равна стороне основания называется ________________________________________________________________ __________________________________________________________________________
11. Выберите верный ответ из числа предложенных. 1. Чему равна площадь боковой поверхности куба с ребром 10 см?
а) 40см2; б) 400см2; в) 100см2; г) 400см.
2. Чему равна площадь полной поверхности куба с ребром 6 см?
а) 36см2; б) 144см2; в) 216см2; г) 144см.
3. Чему равна площадь боковой поверхности правильной четырехугольной призмы, если ее высота h, сторона основания a?
а) ha; б) 4ah; в) 42h; г) 4(a+h).
4. Чему равна площадь полной поверхности куба, если его диагональ равна d?
а) 2d2; б) 6d2; в) 3d2; г) 4d.
5. Прямоугольный параллелепипед имеет три измерения, равные a=5см; b=8см; h=10см. Какова площадь его полной поверхности?
а) 400см2; б) 160см2; в) 280см2; г) 340см2.
6. Сколько всего диагоналей можно провести в четырехугольной призме?
а) 2; б) 4; в) 6; г) 8.
1.3. Практическое решение задач.
1. Ознакомьтесь с условием задачи и разберите ее решение.
В основании прямой призмы лежит равнобедренный треугольник с основанием, равным 6см., и углом при вершине 1200. Диагональ боковой грани, содержащей основание равнобедренного треугольника, равна 10см. Найдите площадь боковой поверхности призмы.
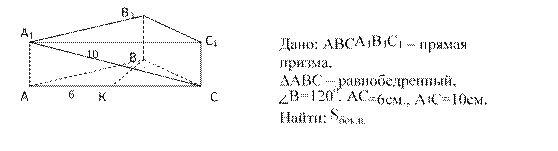
Решение.
1. В
плоскости![]() рассмотрим ΔАВС. Проведем ВК⟘АС.
рассмотрим ΔАВС. Проведем ВК⟘АС.
2. АК=КС, ∠1=∠2 (свойство высоты равнобедренного треугольника)
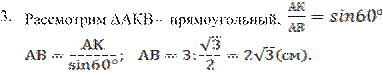
4. Рассмотрим ΔАА1С – прямоугольный.
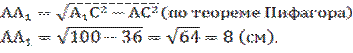
5. Sбок.п. = РΔАВС·АА1=(2АВ+АС)·АА1;
Sбок.п =
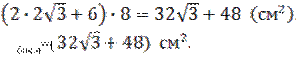 Ответ: S
Ответ: S
2. Проанализируйте решение задачи и допишите в приведенном решении нужные обоснования.
Каждое ребро правильной шестиугольной призмы равно 4 см (достройте рисунок). Найдите площадь ее боковой и полной поверхностей.
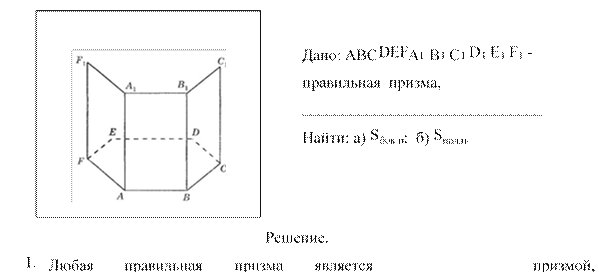
следовательно, площадь ее боковой поверхности равна_________________________________периметра ______________на ____________________призмы, т. е. Sбок = Р * ______, где Р = _______* 6 = ______ (см), h = ______ см.
Таким образом, S бок = _________*________ = _______(см2).
2. Площадь полной поверхности _____________________________ любой призмы равна ___________________ площадей________________ее граней. т.е.
Sпол = ______ + 2 ________. Основание данной призмы -
___________________ шестиугольник со
стороной а = 4 см, следовательно, Sосн ![]() _______= _________* 42
= _______(см2).
_______= _________* 42
= _______(см2).
Итак, Sпол = (_______ + __________) см2.
Ответ: S бок =___________, Sпол = ____________.
3. Ознакомьтесь с условием задачи и запишите ее решение по указанному плану.
Дано: АВСА1В1С1 – прямая
 треугольная призма, АС =
ВС, угол АВС = 90˚, ВN = NA, угол CNC1 = 45˚,CC1 = 6
треугольная призма, АС =
ВС, угол АВС = 90˚, ВN = NA, угол CNC1 = 45˚,CC1 = 6
Решение:
План: 1. ___________________________
1. Определите углы и вид ______________________________ треугольника СС1N, найдите СN 2. ___________________________
2. 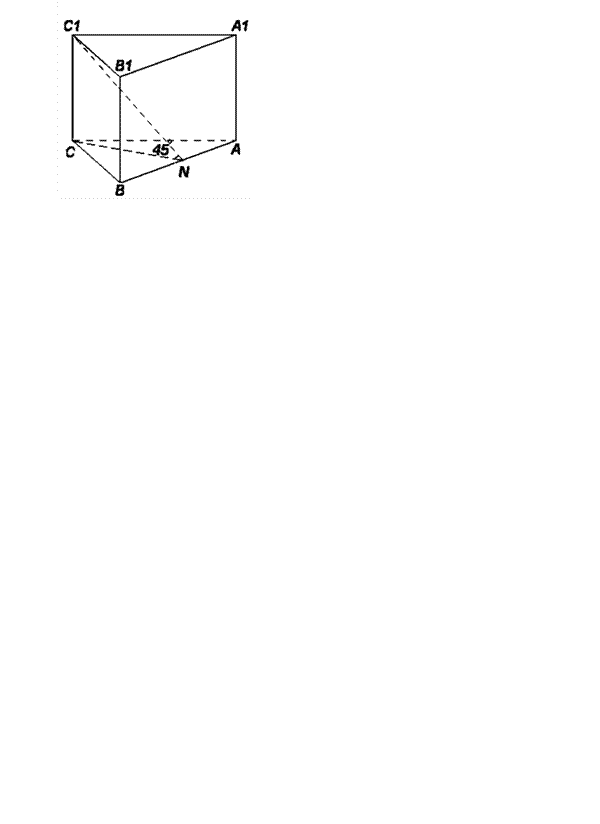 Определите углы и
вид треугольника
СВN, найдите ВN ______________________________ 3. Вычислите площадь треугольника 3.
___________________________ АВС,
определив чем является в ______________________________ этом треугольнике СN 4.
___________________________
Определите углы и
вид треугольника
СВN, найдите ВN ______________________________ 3. Вычислите площадь треугольника 3.
___________________________ АВС,
определив чем является в ______________________________ этом треугольнике СN 4.
___________________________
4. Вычислите объем
______________________________
4. Решите задачи. Ответ:
1. В прямоугольном параллелепипеде стороны основания равны 25 и 3. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.
Дано: __________________________
_______________________________ _______________________________
Найти: _____________________
|
Решение |
______________________________________________________________
______________________________________________________________________ ______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________ 16 ______________________________________________________________________
Ответ: _______________________________________________________
2. В правильной n-угольной призме сторона основания равна а и высота равна h. Вычислите площади боковой и поной поверхности призмы, если: n = 4, а = 12 дм, h = 8 дм
|
|
Дано: __________________________
_______________________________
_______________________________
 Найти: ______________________
Найти: ______________________
Решение _______________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________ ______________________________________________________________________
 ______________________________________________________________________
Ответ:
_______________________________________________________
______________________________________________________________________
Ответ:
_______________________________________________________
3. Сторона основания правильной треугольной призмы равна 6см., а диагональ боковой грани равна 10см. Найти площадь боковой и полной поверхности призмы.
Дано: __________________________
_______________________________

 _______________________________
Найти:
_________________________
_______________________________
Найти:
_________________________
Решение ______________________________________________________________
______________________________________________________________________ ______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
5 ________________________________. Выполните задания. ______________________________________
______________________________________________________________________
1Ответ:. Составьте зад ________________________________ачу на нахождение площади полной поверхности_______________________ прямоугольного параллелепипеда. Решите еѐ.
Задача: ___________________________________________________________________ __________________________________________________________________________ __________________________________________________________________________
__________________________________________________________________________


Решение ______________________________________________________________
______________________________________________________________________
 ______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
Ответ:________________________________________________________
2. Составьте задачу на нахождение объема прямой призмы. Решите еѐ.
Задача: ___________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________ __________________________________________________________________________
Дано: __________________________

 _______________________________
_______________________________
Найти:
_________________________
_______________________________
_______________________________
Найти:
_________________________
Решение _______________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
Ответ: _______________________________________________________
1. Дана прямая четырехугольная призма со сторонами основания 4 и 6 см. Боковое ребро призмы равно 12 см. Вычислите Sполн. и V призмы
2. Дана прямая четырехугольная призма со сторонами основания 5 и 7 см. Боковое ребро призмы равно 8 см. Вычислите диагональ призмы.
3. Дан прямоугольный параллелепипед с измерениями 5, 7, и 10 см. Найдите диагональ параллелепипеда.
4. Диагональ
куба равна ![]() . Найдите его объем.
. Найдите его объем.
5. Дана прямая четырехугольная призма со сторонами основания 6 и 5 см. Боковое ребро призмы равно 12 см. Вычислите диагональ призмы и ее объем
Рассмотрим плоскость ![]() , многоугольник
, многоугольник
![]() ,
лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами
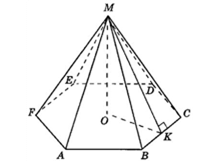
многоугольника. Полученный при этом многогранник называется пирамидой.
,
лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами
многоугольника. Полученный при этом многогранник называется пирамидой.
 Рис. 3
Рис. 3
называются боковыми ребрами. Многоугольник A A …A
называется основанием, а треугольники с общей вершиной – боковые грани. Точка S — вершиной пирамиды
Высота пирамиды – перпендикуляр SP, проведенный из вершины пирамиды к плоскости основания.
В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), пятиугольной (n=5) (рис. 4) и так далее. Альтернативное название треугольной пирамиды – тетраэдр.
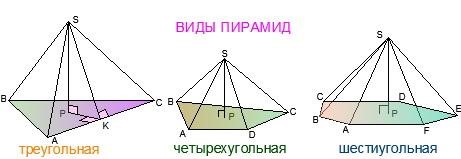
Рис. 4
Площадь полной поверхности пирамиды равна сумме площадей всех ее граней:
Sполн. = Sосн .+ Sбок.,
где Sосн – площадь основания, Sбок – площадь боковой поверхности пирамиды. Площадью боковой поверхности пирамиды называется сумма площадей ее боковой грани

 Пирамида
называется правильной, если еѐ основание – правильный
многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания,
является еѐ высотой.
Пирамида
называется правильной, если еѐ основание – правильный
многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания,
является еѐ высотой.
Все боковые грани правильной пирамиды - равные
равнобедренные треугольники.
Площадь боковой поверхности правильной пирамиды вычисляется по формуле:
Sбок. = ½ ∙ Pосн ∙ d,
где Р – периметр основания пирамиды, d – апофема (высота боковой грани, проведенная из вершины).
Объем пирамиды вычисляется по формуле:
V
![]() ,
,
где Sосн – площадь основания пирамиды, h – высота пирамиды.

Перпендикуляр, проведенный из какой – либо точки одного основания к плоскости другого основания, называется высотой усеченной пирамиды. На рисунке СН – высота усеченной пирамиды.
Боковые грани усеченной пирамиды представляют собой трапеции.
Усечѐнная пирамида, полученная из правильной пирамиды, сечением, параллельным еѐ основанию, называется правильной усечѐнной пирамидой.
Основания правильной усеченной пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называется апофемами.
Площадь боковой поверхности усеченной пирамиды равна сумме площадей ее боковых граней.
Площадь боковой поверхности правильной усечѐнной пирамиды равна произведению полусуммы периметров оснований на апофему.
Sбок ![]() ,
,
где Р, р – периметры оснований пирамиды, h – апофема.
Площадь полной поверхности усеченной пирамиды равна сумме площадей оснований и площади боковой поверхности пирамиды. Объем усеченной пирамиды вычисляется по формуле:
![]() V
V ![]() h(SS1 S*S1) ,
h(SS1 S*S1) ,
где h – высота усеченной пирамиды, S и S1 - площади оснований усеченной пирамиды.
1. Выполните чертеж четырехугольной пирамиды, обозначьте ее и запишите:

 вершины _____________________
боковые
ребра ____________________ боковые
грани ____________________ _________________________________
основание________________________
вершины _____________________
боковые
ребра ____________________ боковые
грани ____________________ _________________________________
основание________________________
_________________________________
2. Закончите предложения.
1. Высотой пирамиды называется _____________________________________________ __________________________________________________________________________
2. Пирамида называется правильной, если ______________________________________
__________________________________________________________________________ 3. Апофемой правильной пирамиды называется _________________________________ __________________________________________________________________________
4. Площадью полной поверхности пирамиды называется _________________________ __________________________________________________________________________
5. Площадью боковой поверхности пирамиды называется ________________________ __________________________________________________________________________ 6. Усеченная пирамида – нижний многогранник, отсекаемый от пирамиды плоскостью, параллельной __________________________________________________ __________________________________________________________________________ 7. Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью ___________________________________________
__________________________________________________________________________
8. Выпуклый многогранник называется правильным, если ________________________ __________________________________________________________________________
9. Примеры моделей пирамиды и правильных многогранников из вашей профессии: _
__________________________________________________________________________
3. Ответьте на вопросы:
1. Сколько сторон основания, боковых ребер, вершин имеет семиугольная пирамида? __________________________________________________________________________ 2. Сколько оснований у усеченной пирамиды? __________________________________
__________________________________________________________________________ 3. Какие многоугольники лежат в основаниях правильной усеченной шестиугольной пирамиды? ________________________________________________________________ __________________________________________________________________________
4. Сколько боковых граней у шестиугольной пирамиды? ________________________
__________________________________________________________________________
5. Как называется точка пресечения всех боковых ребер пирамиды? _______________
__________________________________________________________________________ 6. В каком взаимном расположении находятся ребро основания и апофема пирамиды? _____________________________________________________________
__________________________________________________________________________
7. Какая фигура может лежать в основании прямой четырехугольной пирамиды? ___
__________________________________________________________________________
8. Из каких фигур состоит пирамида?_________________________________________
__________________________________________________________________________ 9. Сколько боковых ребер и сторон основания у десятиугольной пирамиды? _______ __________________________________________________________________________ 10. Сколько боковых ребер и сторон основания у семиугольной усеченной пирамиды? __________________________________________________________________________
11. Сколько (и какие) виды правильных выпуклых многогранников Вы знаете? _____ __________________________________________________________________________ 12. Какое наименьшее число ребер, граней, вершин имеет правильный многогранник? Как он называется? _________________________________________________________ 13. Всякий ли параллелограмм может быть основанием правильной пирамиды?
Ответ поясните ________________________________________________________
__________________________________________________________________________
__________________________________________________________________________ 14. Может ли правильный многоугольник быть основанием неправильной пирамиды?
Ответ поясните ________________________________________________________
__________________________________________________________________________
__________________________________________________________________________ 15. Основанием треугольной пирамиды является равносторонний треугольник. Одна из боковых граней ее перпендикулярна к плоскости основания. Является ли данная пирамида правильной?
 Ответ поясните
рисунком и соответствующими записями. _____ ________________________________
________________________________ ________________________________
Ответ поясните
рисунком и соответствующими записями. _____ ________________________________
________________________________ ________________________________
____________________________22
____________________________
____________________________ ____________________________
4. Выполните задания.
1. Среди изображенных тел выберите номера тех, которые являются пирамидами.
![]()
![]()
1 2 3 4 5 6 7
Ответ: ____________________________________________________________________
2. SABCD – правильная четырехугольная пирамида. Проведите высоту SO. Как определить угол между боковым ребром пирамиды и плоскостью основания? Чему равен этот угол, если предположить, что высота SO вдвое меньше бокового ребра?
Ответ поясните _________________
________________________________
 ________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
3.Сделайте рисунок пятиугольной усеченной пирамиды, обозначьте ее и запишите:
 а) боковые ребра
_________________ ________________________________
б) основания
_____________________
а) боковые ребра
_________________ ________________________________
б) основания
_____________________
________________________________
|
пирамиде. |
4. Проведите диагональное сечение в правильной четырехугольной усеченной
Поясните рассуждения. ___________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
 ________________________________
________________________________
6. Поясните, что является осью симметрии:
а) квадрата ________________________________________________________________
б) окружности _____________________________________________________________
в) правильного треугольника _________________________________________________ г) параллелограмма
д) ромба
5. Заполните пропуски, чтобы утверждение было верным.
1. Каждая точка высоты правильной пирамиды равноудалена от всех ___________________________________________ основания.
2. Боковыми гранями правильной пирамиды являются ___________________________ __________________________________________________________________________ 3. Площадь боковой поверхности правильной пирамиды равна произведению полупериметра основания на _________________________________________________ __________________________________________________________________________ 4. Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на _____________________________ __________________________________________________________________________
5. Боковыми гранями правильной усеченной пирамиды являются _________________
__________________________________________________________________________
6. Каждая точка высоты правильной пирамиды равноудалена от всех _________________________________________________ граней.
7.У правильной пирамиды:
а) боковые грани ___________________________________________________________
б) боковые ребра ___________________________________________________________
в) двугранные углы при основании ____________________________________________
г) двугранные углы при боковых ребрах _______________________________________
д) апофемы ________________________________________________________________ 8. Диагональное сечение усеченной пирамиды – сечение ее плоскостью, проходящей через два _________________________________________________________________ боковых ребра пирамиды.
6. Выберите верный ответ из числа предложенных.
1. Чему равна высота правильной треугольной пирамиды со стороной основания a и боковым ребром b?
а) ![]() ; б)
; б) 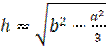 ;
в)
;
в) ![]() .
.
2. Чему равна сторона основания правильной шестиугольной пирамиды, если ее высота hи боковой ребро b?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
3. Сколько плоскостей симметрии имеет правильная четырехугольная пирамида?
а) 1; б) 3; в) 4.
4. Выберите правильную формулу для нахождения площади полной поверхности правильной пирамиды
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
где h – высота,l– апофема, P– периметр основания
5. Чему равна апофема правильной шестиугольной пирамиды со стороной основания a и высотой h?
а) 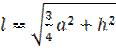 ; б)
; б) ![]() ;
в)
;
в) ![]() .
.
6. Чему равна апофема правильной треугольной пирамиды со стороной основания aи боковым ребром b?
а) ![]() ; б)
; б) 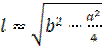 ; в)
; в) ![]() .
.
7. Чему равна апофема правильной четырехугольной пирамиды со стороной основания a и высотой h?
а) ![]() ; б)
; б) ![]() ; в)
; в)
![]() .
.
8. Чему равна высота правильной шестиугольной пирамиды со стороной основания a и боковым ребром b?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
9. Имеет ли правильная пятиугольная пирамида ось симметрии?
а) да; б) нет.
7. Выполните задание.
1. Постройте правильную пирамиду и выделите угол между одним из ее боковых ребер и плоскостью основания.

2. Постройте произвольную пирамиду, в основании которой лежит квадрат. Можно ли еще построить пирамиды с этим же основанием? Если да, то сколько? Ответ аргументируйте чертежом.
|
|
|
3. Постройте правильную треугольную пирамиду. Выпишите все ребра, которые пересекаются с основанием пирамиды.

4. Постройте четырехугольную пирамиду. Постройте отрезки, соединяющие середины боковых ребер пирамиды. Выпишите все пары параллельных отрезков.
|
|
 ____________________________
____________________________
____________________________
____________________________
____________________________
____________________________
5.
 |
|
6 плоскости основания. |
|
|
|
|
|
|
____________________________
 ____________________________
____________________________ ____________________________
____________________________
____________________________ ____________________________
____________________________
. Постройте четырехугольную пирамиду, одно ребро которой перпендикулярно
7. Постройте треугольную пирамиду, одна грань которой перпендикулярна плоскости основания.
8. Докажите.
Докажите, что площадь боковой поверхности правильной пирамиды равна половине произведения периметра на основание.
Дано:_______________________________________
 ____________________________________________
____________________________________________
Доказательство: _____________________________
 ____________________________________________
____________________________________________
____________________________________________
____________________________________________
____________________________________________
____________________________________________
____________________________________________
2.3. Практическое решение задач. ________________________________ ____________
1. Ознакомьтесь с условием задачи и разберите ее решение.
В правильной четырехугольной пирамиде высота равна 4 см., а боковое ребро – 5 см. Найдите угол, образованный боковым ребром с плоскостью основания.

Решение:
1. SD- - наклонная к α, SO⟘α, значит ОD – проекция SD на плоскость α (ОD= прαSD).
2. ∠(SD,α)=∠SDО (по определению).
3. SO⟘α, ОD![]() α,
следовательно, SO⟘ОD
(по определению прямой, перпендикулярной плоскости).
α,
следовательно, SO⟘ОD
(по определению прямой, перпендикулярной плоскости).
4. ΔSOD – прямоугольный (по п.3).4
![]()
Ответ: ![]()
3. Проанализируйте решение задачи и допишите в приведенном решении нужные обоснования.
Боковое ребро правильной шестиугольной пирамиды равно 5 см, а сторона основания
– 6 см. найдите площадь ее боковой и полной поверхности
Решение:
 Площадь боковой поверхности
правильной
пирамиды равна
произведению___________ основания
на _________________________,
Площадь боковой поверхности
правильной
пирамиды равна
произведению___________ основания
на _________________________,
т. е. Sбок = _____ * d, где d = MK ![]() ,
CK
,
CK ![]() ___ =____(см).
___ =____(см).
Итак, d ![]() , Р
= 6 * ___ =
, Р
= 6 * ___ =
= _______(см), Sбок = _____ * _____ = _____(см2).
2)
Sпол = _________ + Sосн, где Sосн ![]() =
______
=
______![]() (см2).
(см2).
Следовательно, Sпол = _______+____________(см2).
Ответ: Sбок =____________, Sпол =_______+____________(см2).
4. Ознакомьтесь с условием задачи и запишите ее решение по указанному плану.
5.
В правильной четырехугольной пирамиде боковое ребро, равное 10 дм., образует с плоскостью основания угол равный 600. Найдите высоту пирамиды.


4. Решите задачи.
1. Апофема пирамиды равна 5см., а высота 4см. Найдите площадь полной поверхности пирамиды
Дано: __________________________
 _______________________________
_______________________________
_______________________________28
Найти: _________________________
Решение _______________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________ Ответ: _________________________________________________________________
 2.Основанием пирамиды DABC
является правильный треугольник ABC, сторона которого равна a.
Ребро DA перпендикулярно к плоскости ABC, а плоскость DBC
составляет с плоскостью ABC угол 30°. Найдите площадь боковой
поверхности пирамиды.
2.Основанием пирамиды DABC
является правильный треугольник ABC, сторона которого равна a.
Ребро DA перпендикулярно к плоскости ABC, а плоскость DBC
составляет с плоскостью ABC угол 30°. Найдите площадь боковой
поверхности пирамиды.
Дано: __________________________
_______________________________

 _______________________________
Найти:
_________________________
_______________________________
Найти:
_________________________
Решение ______________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
3.Ответ: Найдите объѐм правильной пирамиды, если боковое ребро равно 3см, а сторона _______________________________________________________ основания – 4см.
Дано: __________________________
_______________________________
_______________________________
Найти: _________________________
Решение ______________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________ _____________________________________________________________________
29
Ответ: _______________________________________________________
5. Выполните задания.
1. Составьте задачу на нахождение объема прямой пирамиды. Решите еѐ.
Задача: ___________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
__________________________________________________________________________
Дано: __________________________
_______________________________

 _______________________________
Найти:
_________________________
_______________________________
Найти:
_________________________
Решение _______________________________________________________________
______________________________________________________________________
______________________________________________________________________ ______________________________________________________________________
____________________________________________________________
Ответ: _________________________________________________________________
2. Составьте задачу на нахождение объема правильной пирамиды. Решите еѐ.
Задача: ___________________________________________________________________
__________________________________________________________________________ __________________________________________________________________________

Решение _______________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
 Ответ:
_______________________________________________________
Ответ:
_______________________________________________________
1. Дана правильная четырехугольная пирамида со стороной основания 4см. высота пирамиды равна 5 см. Найдите боковое ребро пирамиды и ее объем.
2. В основании пирамиды лежит прямоугольник со сторонами 3см. и 4см. Высота пирамиды равна 8 см. Найдите площадь полной поверхности пирамиды.
3. Основанием пирамиды служит равнобедренный треугольник, у которого основание равно 12см., а боковая сторона - 10см. Боковые грани образуют с основанием равные двугранные углы, содержащие по 45°. Найдите высоту пирамиды.
4. Высота и апофема правильной четырехугольной пирамиды соответственно равны 4 и 17 см. Вычислите объем пирамиды.
5. Основание пирамиды – квадрат. Сторона основания равна 20 дм, а еѐ высота равна 21 дм. Найдите объѐм пирамиды.
Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.
Все ребра правильного многогранника — равные отрезки, все плоские углы правильного многогранника также равны.
Существует пять различных правильных многогранников (выпуклых): куб, правильный тетраэдр, правильный восьмигранник (правильный октаэдр), правильный двенадцатигранник (додекаэдр), правильный двадцатигранник (икосаэдр).
В приведенных ниже формулах использованы следующие обозначения: V — объем многогранника, S — площадь поверхности, R — радиус описанной сферы, r — радиус вписанной сферы, Н — высота многогранника, а — каждое из равных ребер многогранника. а) Куб
Все шесть граней куба — равные квадраты (рис. 5).
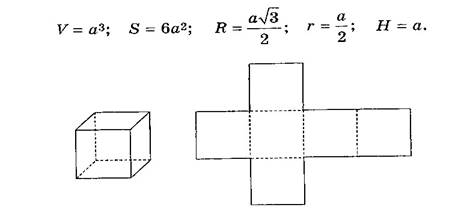
Рис. 5
б) Правильный тетраэдр
Все четыре грани — равные правильные треугольники (рис. 6).
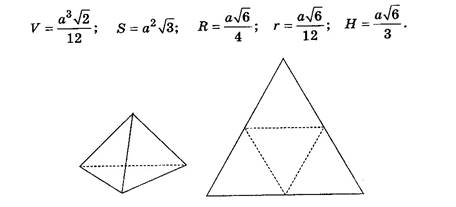
Рис. 6
в) Правильный октаэдр Все восемь граней — равные правильные треугольники (рис. 7).
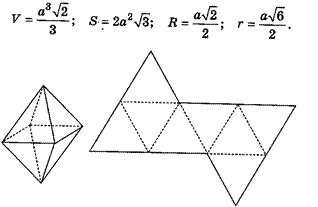
Рис.7
г) Правильный додекаэдр
Все двенадцать граней — равные правильные пятиугольники (рис.8). Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Сумма плоских углов при каждой вершине додекаэдра равна 324°.
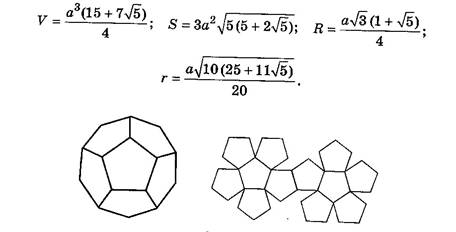
Рис. 8
д) Правильный икосаэдр
Все двадцать граней — равные правильные треугольники (рис. 9). Каждая вершина икосаэдра является вершиной пяти треугольников. Сумма плоских углов при каждой вершине икосаэдра равна 300°.
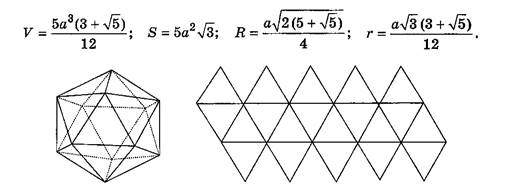
Рис. 9
1. Заполните пропуски
1.Выпуклый___________________________________называется правильным, если________его грани - ________________________________многоугольники, и в __________________его_________________________________сходится одно и то же число.
2.Существует_________________правильных многогранников.
3. Тетраэдром называется_______________________________________________________
_____________________________________________________________________________.
4.Кубом называется____________________________________________________________ _____________________________________________________________________________.
5.Октаэдром называется________________________________________________________ _____________________________________________________________________________.
Икосаэдром называется_________________________________________________________ _____________________________________________________________________________.
6. Додекаэдром называется_____________________________________________________ __________________________________________________________________________.
2.Докажите, что куб является правильным многогранником.
Доказательство:
Проверим, обладает ли куб всеми признаками правильного _________________________, указанными в определении.
1) Куб______________________ выпуклым многогранником.
2) Каждая грань куба - ______________________, т. е. ___________________________ многоугольник, и все грани_______________________ между собой
3)
![]() В_______________________ вершине куба сходится
___________________ число ребер, а именно _____ребра.
В_______________________ вершине куба сходится
___________________ число ребер, а именно _____ребра.
![]() Итак, у
куба____________________ все признаки, указанные в
определении________________________ многогранника. Следовательно,
куб_______________
Итак, у
куба____________________ все признаки, указанные в
определении________________________ многогранника. Следовательно,
куб_______________
правильным_____________________, что и требовалось доказать.
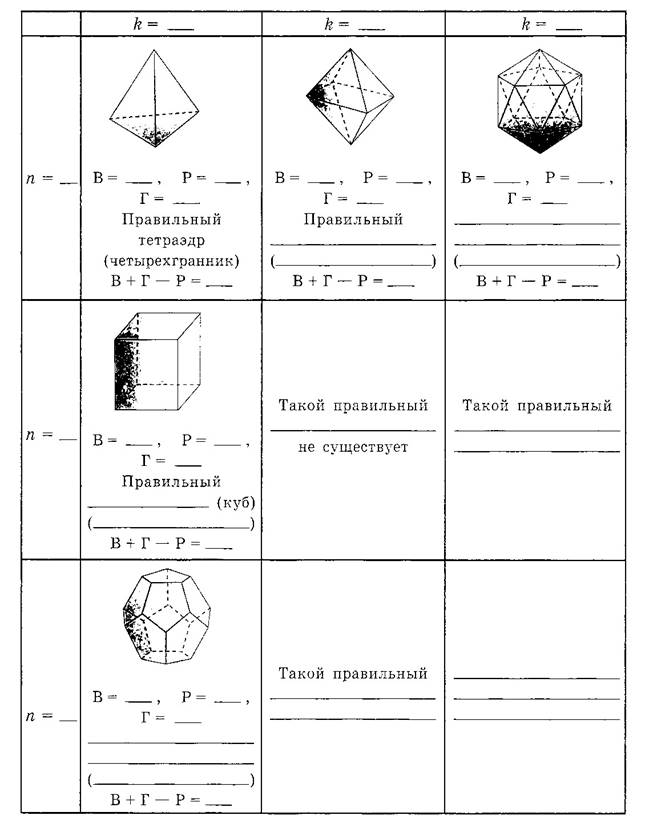
2.Запишите в таблицу значения параметров: n — число сторон грани правильного многогранника; k — число ребер, сходящихся в одной вершине; В — число вершин многогранника; Р — число ребер; Г — число граней. Напишите названия многогранников.
Вычислите для каждого из них величину В + Г – Р.
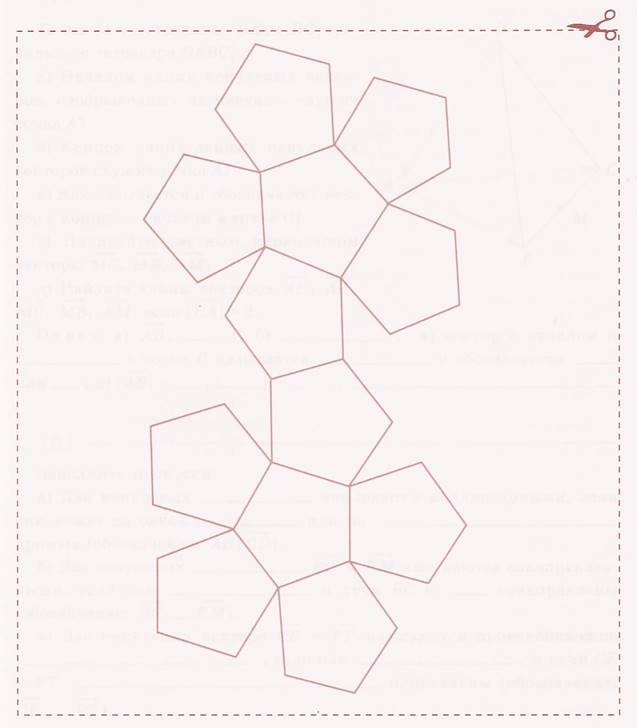
3. а) Дорисуйте на развертке правильного додекаэдра клапаны для склеивания, добавляя их через одно ребро. Вырежите развертку и склейте модель многогранника.
б) Измерьте длину ребра и вычислите площадь поверхности правильного додекаэдра.
Ответ. б) см2.
4.а) Дорисуйте на развертке правильного икосаэдра клапаны для склеивания, добавляя их через одно ребро. Вырежите развертку и склейте модель многогранника.
б) Измерьте длину ребра и вычислите площадь поверхности правильного икосаэдра.
Ответ. б) см2.
-
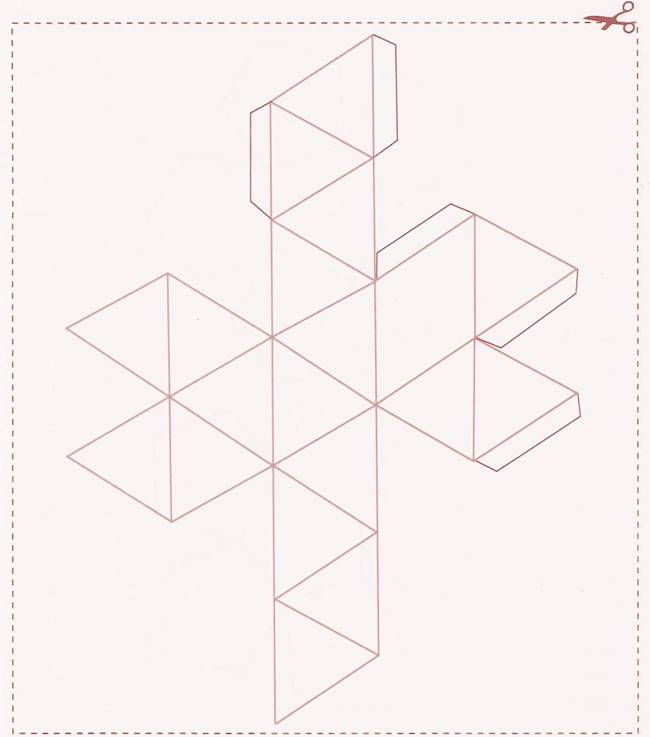
5. а) Дорисуйте на развертке правильного додекаэдра клапаны для склеивания, добавляя их через одно ребро. Вырежите развертку и склейте модель многогранника.
б) Измерьте длину ребра и вычислите площадь поверхности правильного додекаэдра.
Ответ. б) см2.

1. Алешина Т. Н. Обучающие и проверочные задания. Геометрия. 10 класс (Тетрадь)/ Алешина Т. Н. – М: Интелект – Центр. – 2011. – 108 с.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., « Геометрия: учебник для 10-11 кл.» - М: Просвещение, 2009.-256 с.
3. Глазков Ю. А., Юдина И.И. Геометрия 10 класс. Рабочая тетрадь: учебное пособие для общеобразоват. учреждений (базовый и профильный уровни) / М.:
Просфещение, 2011. – 95 с.
4. Евдокимов Н. ИН. Краткий справочник по математике. 9 – 11 классы. – СПб.:
Издательский Дом «литера», 2010. – 288 с.
5. Смирнова И.М. Геометрия 10 класс. Рабочая тетрадь: учебное пособие для общеобразоват. учреждений/ И. М. Смирнова, В. А. Смирнов. – М.: Мнемозина, 2009. – 103 с.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.