Работа

Комбинаторика – 1

Часть 1

Историческая справка:

Возникновение комбинаторики относится к 17 веку. Первоначально комбинаторные задачи касались, в основном, азартных игр – вопросов, сколькими способами можно выбрать (выбросить) данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре. Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Теоретическое исследование вопросов проводили в 17 веке французские ученые Паскаль и Ферма. Исходным пунктом исследований тоже были проблемы азартных игр. Дальнейшее развитие комбинаторики связано с именами Якова Бернулли, Лейбница, Эйлера.

«Комбинаторика – 1» - это те задачи, которые полезно рассмотреть на кружках или элективных курсах для младших школьников в 6-8 кл. (7-9 кл.).

 I.       

№1. В магазине «Все для чая» есть 5 разных чашек и  3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?

№2. В магазине «Все для чая» есть еще 4 разные чайные ложки. Сколькими способами можно купить комплект из чашки, блюдца, ложки?

№3. В стране Чудес есть три города: А, Б, В. Из города А в город Б идет 6 дорог, а из города Б в город В – 4 дороги. Сколькими способами можно проехать от А до В?

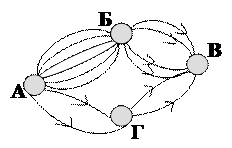№4. !  В стране чудес построили еще один город – Г  и несколько новых дорог.

Сколькими способами можно теперь добраться из города А в город В?

№5. !   В магазине «Все для чая» по-прежнему продается 5 чашек, 3 блюдца, 4 чайные ложки. Сколькими способами можно купить два предмета с разными названиями?

II.                   

№6. Назовем натуральное число «симпатичным», если в его записи встречаются только нечетные цифры. Сколько существует 4-значных «симпатичных» чисел?

Методическое замечание.

В этой задаче ответ имеет вид « mⁿ». Т.е. на каждом из n – мест может быть поставлен элемент из некоторого m – элементного множества.           mⁿ?

№7. Монету бросают трижды. Сколько разных последовательностей орлов и решка можно при этом получить?

№8. Каждую клетку квадратной таблицы 2 х 2 можно покрасить в черный или белый цвет. Сколько существует различных раскрасок этой таблицы?

№9. Сколькими способами можно заполнить вариант в «Спортпрогнозе»? В этой лотерее надо предсказать итог 13 спортивных матчей. Итог каждого матча – победа одной из команд или ничья (счет роли не играет).

III.       

№10. В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколькими способами это можно сделать?

№11. Сколькими способами можно сделать 3-х-цветный флаг с горизонтальными полосами одинаковой ширины, если имеется материал 6 различных цветов?

№12. Сколькими способами можно поставить на шахматную доску белую и черную ладью так, чтобы они не били друг друга?

№13.  Сколькими способами можно поставить на шахматную доску белого и черного королей так, чтобы получилась допустимая правилами игры позиция?

IV.       

Пусть n € N, тогда 1·2·3·…·n=n!

Упражнения: Вычислить:

а.       ,

б.      ,

в.      ,

г.       .

№14. Сколько существует трехзначных чисел, в записи которых цифры 1,2,3 встречаются ровно один раз?

№15. Сколькими способами можно выложить в ряд красный, синий, черный и зеленый шарики?

№16. Сколькими способами можно выложить n разных предметов в ряд из n – мест?

V.       

Введем следующее соглашение: словом будем называть любую конечную последовательность букв русского алфавита.

1)      используя буквы по 1 разу, □ □ □, 6 слов.

2)      «А» - дважды, «Б» - 1раз, «ААБ», «АБА», «БАА», 3 слова.

Сколько различных слов можно получить, переставляя буквы того или иного слова?

№17. «ВЕКТОР».

№18. «ЛИНИЯ».

№19. «ПАРАБОЛА».

№20. «БИССЕКТРИСА».

№21. «МАТЕМАТИКА».

№22. В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?

№23. Сколько диагоналей в выпуклом n – угольнике?

№24. Бусы – это кольцо, на которое нанизаны бусины. Бусы можно поворачивать, но не переворачивать. Сколько различных бус можно сделать из 13 разноцветных бусин?

№25. Предположим, что бусы можно и переворачивать. Сколько тогда различных бус можно сделать из 13 разноцветных бусин?

VI.                                                                         

№26. Сколько существует шестизначных чисел, в записи которых есть хотя бы одна четная цифра?

№27. В алфавите племени Бум-Бум шесть букв. Словом является любая последовательность из шести букв, в которой есть хотя бы две одинаковые буквы. Сколько слов в языке племени Бум-Бум?

Методическое замечание.

Задачи разбиты на шесть групп, каждой группе задач полезно посвящать отдельное занятие. При этом необходимо возвращаться к уже пройденному материалу.  Ученикам необходимо предложить составить новые задачи к каждой группе, предложить их решить  на  кружке с одноклассниками.

Представленный материал взят из книги «Ленинградские математические кружки», г.Киров, 1994г., С.А.Генкин, И.В., Д.В. Фомин.