Работа на тему «Решение уравнений с обратными тригонометрическими функциями»

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА-ДЕТСКИЙ САД № 36»

МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГОРОДСКОЙ ОКРУГ СИМФЕРОПОЛЬ РЕСПУБЛИКА КРЫМ

 

 

 

 

 

 

 

 

 

 

 

«Решение уравнений с обратными тригонометрическими функциями»

 

 

 

 

 

 

 

 

 

 

РАБОТА

Галан Татьяны Николаевны,

учителя математики

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г. Симферополь 2015г

 

 

 

 

 

 

Вспомним важнейшие свойства обратных тригонометрических функций.

 

 

Функция  определена и монотонно возрастает на отрезке [- 1; 1];

.

Функция  определена и монотонно убывает на отрезке [- 1; 1];

 

Функция  определена и монотонно возрастает на R;

.

 

Функция  определена и монотонно убывает на R;

 

                          

 

 

 

     Решение уравнений, левая и правая части которых являются одноименными обратными тригонометрическими функциями различных аргументов, основывается на свойстве монотонности этих функций. Поэтому справедливы следующие равносильные переходы.

1).

2).

3).

4).

 

    При решении уравнений ,  левая и правая части которых являются разноименными обратными тригонометрическими функциями различных аргументов, пользуются известными тригонометрическими тождествами.

Переходы	Использована формула
1.
2.

 Корнем каждого из уравнений (1) – (4) может быть только такое число х, для которого  В противном случае множество значений левой и правой частей уравнения не пересекаются.

 

Пример 1. Решите уравнение .

Решение

;                                           ОДЗ:

arccos x= + 2n, nZ ; arccos x=  + 14, nZ. Поскольку

0 arccos x, то последнее уравнение не выполняется ни при каких значения nZ. Следовательно, исходное уравнение не имеет корней.

Ответ: корней нет.

Пример 2. Решите уравнение 2arcsin x=9.

Решение

2arcsin x=9; arcsin x=  = 4,5.

Следовательно, уравнение решений не имеет, так как

Ответ: корней  нет.

Пример 3. Решите уравнение  arcsin x + arctg.

Решение

arcsin x + arctg;                                                     ОДЗ: |x|

arcsin x=  -  arctg . Найдем синусы обоих частей уравнения:

sin = sin. Следует обратить внимание, что полученное уравнение может быть не равносильным исходному, поэтому его решение обязательно нужно подставить в исходное уравнение. Из последнего уравнения имеем:

x = sin= sin  cos- cos  sin= .

Рассчитаем cos. Пусть  = ,  , тогда tg=. Но поскольку tg то  , то есть угол находиться в певой четверти единичного круга.

Найдем теперь cos.

1+= ;   = 1+   = ;  = ;

cos =  (cos).

Найдем sin= 1 –  = 1 –   = ;

sin  (sin).

X=  =   = .

Ответ: .

Примечание. Если sin = sin, причем , то .

Сделаем проверку arcsin; arctg=.

Поскольку 0 arcsinи 0 – arctg, то   и  ,

причем X= найдено при условии, что sin , значит .

Пример 4.

Решить уравнение  2.

Решение

2. Если известно,  – тогда

2(  -)+=

Ответ:-1

Пример 5.

Решить уравнение    

   

ОДЗ: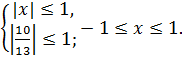

=

- 10)=0; x=0 или 13-5=0;

=; 1-=; =;

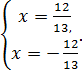
Проверка

1)  X=0; 2arcsin0=0; arcsin0=0; 0=0-правильно.

2)   X=; 2arcsinarcsin (так как  arcsin

2arcsin (так как , поэтому, arcsin ,

то есть 2arcsin). Тогда x= –не является корнем.

3)x=-2arcsin(- arcsin(). Значит x=-  -не является корнем.

Ответ:0.

Пример 6.

Решить уравнение

Решение

ОДЗ:|sinx|.

Имеем

Так как  . Значит, x=0.

Ответ:0

Пример 7.

Решить уравнение

Решение

  Пусть arcsinx=t,

ОДЗ:|x|.

|t|

Ответ:-sin1,5.

Пример 8.

Решить уравнение =-.

Решение

=- ;

ОДЗ: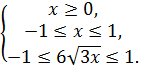

–

6x=; 36=1-108; 144=1; = ; x=

Проверка:

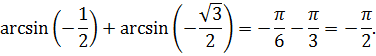
Значит, x=-  -корень уравнения; x= – не является корнем.

Ответ:-.

 

 

 

Пример 9.  Решите уравнение

Решение.

 

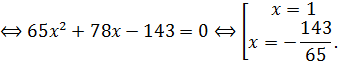
Корень  является посторонним.

Ответ:1

 

Пример 10. Решите уравнение 

Решение. Пусть  Тогда

Пусть Тогда 

Тогда исходное уравнение примет вид

Тогда

Поэтому

 

Ответ:0,1.