Рациональные способы решения задач на смеси, растворы и сплавы

Александровская окружная научно-практическая конференция школьников «Юность. Наука. Культура

 

Секция: физико-математическая

 

 

 

 

 

 

 

 

Название работы «Рациональные способы решения задач

 на смеси, растворы и сплавы»

 

 

 

                                                

 

                                                                              

 

 

 

 

Автор работы: Баловнева Анастасия       

Олеговна                         

                                                                

 

 

 

 

 

 

 

Место выполнения работы: село Круглолесское,   МОУ СОШ № 5 имени Советского Союза А.В.Зацепина,

11 класс

Научный руководитель: Кокорева Ирина Васильевна, учитель математики высшей категориии.

 

 

 

 

 

 

 

Январь 2024 г.                                                                                                                          

                                                           Содержание

 

I. Введение……………………………………………………………………...….3

II. Основная часть…………………………………………………………….…...5

1.     Теоретические основы решения задач на смеси, растворы и сплавы……...5

2.     Алгоритм решения задач на смеси, растворы и сплавы……………..……...6

3.     Способы и методы рационального решения задач на смеси, растворы

 и сплавы………………………………………………………………..………7

3.1            Табличный способ решения задач…………………………..……………..7

3.2                   Решение задач методом чаш………………………………...……………8

3.3                   Правило креста или метод Пирсона………………………………...……9

3.4                   Решение задач методом рыбки (старинным способом) ..……………...14

3.5                   Решение задач методом площадей равновеликих

прямоугольников  подобия прямоугольных треугольников…...……...15

   III. Анкетирование учащихся……………………………………………………..17

IV. Заключение……………………………………………………………………19

V. Литература………………….………………………………………………….21

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I. Введение

Всё впереди!

Как мало за плечами!

Пусть химия нам будет вместо рук,

Пусть станет математика очами.

Не разлучайте этих двух подруг.

(М. Алигер)

Тема исследовательской работы «Рациональные способы решения задач на смеси, растворы и сплавы». Просматривая КИМы ЕГЭ, я обратила внимание, что часто в качестве текстовой задачи предлагается задача на сплавы, смеси или растворы. Они также встречаются на уроках химии. В решении химических задач используются алгебраические приёмы. Исследование и анализ ряда задач сводятся к преобразованиям формул и подстановке известных величин в конечную формулу или алгебраическое уравнение. Задачи на смеси, растворы имеют практическую направленность. Например, мы пьём чай и кладем в чашку столько сахара, чтобы не пересластить (создаем нужную концентрацию), а если пересластили, то добавляем воды. Летом мы ходим за грибами, затем их сушим. И мы понимаем, что чем дольше их сушить, тем меньше в них остается воды, при этом масса сухого вещества не меняется.

Я решила заняться этой темой, чтобы повысить свой уровень знаний по математике и химии, а также улучшить навык решения химических задач математическими способами.  В исследовательской работе рассмотрела различные способы решения задач на смеси, растворы и сплавы.

Цель: исследовать разные способы решения задач на смеси, растворы и сплавы и выявить рациональные способы.

Задачи:

·        систематизировать задачи на смеси, растворы и сплавы;

·        научиться решать задачи на смеси, растворы и сплавы разными способами;

·        подготовить буклет для учащихся по решению задач на смеси, растворы и сплавы;

·        сформулировать выводы.

Предмет исследования: способы решения задач на сплавы, смеси и растворы.

Гипотеза: задачи на смеси, растворы и сплавы вызывают у учащихся затруднения, но их решение сводится к определённому алгоритму, который применяется к задачам данного типа.

Методы исследования:

теоретические: анализ, синтез, сравнение, обобщение;

практические: анкетирование учащихся.

Актуальность и практическая ценность работы - возможность использования методов математики при изучении химии. Задачи на смеси – это тип задач, охватывающий довольно большой круг разнообразных ситуаций. Сюда входят задачи на понижение и повышение концентрации, «высушивание», смешивание растворов разных концентраций. При этом для получения нужной и заранее задуманной смеси необходимо четко знать в каком соотношении или в каком количестве нужно взять исходные компоненты. Более того, при решении задач на смеси и сплавы четко прослеживается взаимосвязь математики с другими школьными дисциплинами, например, такими, как физика, химия. А значит, умение решать такие задачи позволит легче ориентироваться и в других сферах.

Итогом исследовательской работы является составление буклета по способам решения задач на смеси, растворы и сплавы с кратким описанием каждого метода и схемами решения.

 

 

 

 

 

II. Основная часть

1.     Теоретические основы решения задач на смеси, растворы и сплавы

Определим, что это за задачи на смеси и сплавы. Довольно часто приходится смешивать различные жидкости, порошки, разбавлять что-либо водой или наблюдать испарение воды.

Раствор.  В 190 грамм воды добавим 10 грамм уксусной кислоты, получим раствор, масса которого равна 190 + 10 = 200 г. Концентрация кислоты (процентное содержание) — это отношение количества уксуса к количеству раствора, записанное в процентах:

,  процентное содержание воды: 

Смесь. У нас есть одно ведро песка и три ведра извести. Смешаем содержимое всех ведер, получим смесь извести с песком, её масса равна 1 + 3 = 4 (единиц массы). Концентрация (процентное содержание песка) — это отношение количества песка к количеству смеси, записанное в процентах:  процентное содержание извести:  .

Сплав. Имеем сплав меди и свинца, в котором 100 г меди и 150 г свинца. Концентрация (процентное содержание меди) – отношение количества меди к количеству смеси в процентах:

Как можно заметить, во всех задачах на сплавы, растворы, смеси используется всего одна формула:

,

где K — процентное содержание чистого вещества в сплаве или растворе,

m –  масса чистого вещества

M — масса сплава или раствора.

Решая задачи данного типа, нам нужно будет выделить компоненты, которые изменяются, и те, что остаются неизменными. Количество компонентов в смеси измеряют в единицах массы, а не объема, так как изменения массы проходят линейно.

При решении задач на сплавы, смеси и растворы принимают некоторые основные допущения:

• Все получающиеся сплавы или смеси однородны.
• Масса смеси нескольких веществ равна сумме масс компонентов.
• Процент - одна сотая любого вещества.  
• Производительность объекта - скорость работы.
• Процентное содержание (концентрация) вещества в смеси показывает долю вещества в растворе.  Это отношение может быть выражено либо в дробях, либо в процентах.
• Сумма концентраций всех компонент, составляющих смесь, равна единице.

 

2.     Алгоритм решения задачи на смеси, растворы и сплавы:

• изучить условие задачи;
• выбрать неизвестную величину (обозначить ее буквой);
• определить все взаимосвязи между данными величинами;
• составить математическую модель задачи (выбрать способ решения задачи, составить пропорцию или уравнение относительно неизвестной величины) и решить ее;
• провести анализ результата.

 

3.     Способы и методы рационального решения задач на смеси, растворы и сплавы

 

  3.1 Табличный способ решения задач

         При решении задач рассматриваемого вида, удобно использовать таблицу, т.к. зрительное восприятие определённого расположения величин в таблице даёт дополнительную информацию, облегчающую процесс решения задачи и её проверки.

Задача 1. Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?

Решение. Составим таблицу

Так как подливали только воду, масса уксусной кислоты в  растворе не изменилась.  Составляем уравнение:

                    0,08(200 + х) = 0,7·200

                    16 + 0,08х = 140

                    0,08х = 124

                     х = 1550

Ответ:1,55 кг воды.

 

  3.2. Решение задач методом чаш

         Метод состоит в следующем: необходимо изобразить каждый сплав (раствор, смесь) в виде прямоугольника. После заполняем получившиеся прямоугольники в соответствии с условием задачи:

1) Над каждым «маленьким» прямоугольником указываем соответствующие компоненты сплава (смеси, раствора).

2) Внутри прямоугольников вписываем процентное содержание соответствующего компонента. Если сплав (смесь, раствор) состоит из двух компонентов, то достаточно указать процентное содержание одного из них. В этом случае процентное содержание второго компонента равно разности 100% и процентного содержания первого.

3) Под прямоугольником записываем массу (или объем) соответствующего сплава (или компонента). И учитывая, что масса сплава (раствора, смеси) нескольких веществ равна сумме масс компонентов, составляем уравнение.

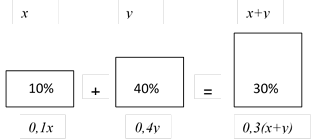
         Задача 2.1. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

         Решение. Пусть масса первого сплава равна х, масса второго равна у. В результате получили сплав массой х+у.

Решив систему, получили х=3, у=6. Таким образом, масса полученного сплава равна 9.

Ответ: 9 кг.

         Задача 2.2. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?

         Решение. Пусть х г – масса первого сплава. Тогда, (800 – х) г – масса второго сплава.

         Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):

 

         Решив это уравнение, получаем x=500.

При этом значении х выражение 800 – x = 300. Это означает, что первого сплава надо взять 500 г, а второго – 300 г.

Ответ: 500 г, 300 г.

 

3.3. Правило креста или метод Пирсона

         В сети Интернет обнаружила метод Пирсона, который применяется для решения задач на растворы, сплавы и смеси.  Метод Пирсона - это удобный и рациональный способ решения задач. Предложил его английский математик, статистик, биолог и философ Карл Пирсон. Данный метод сводит решение задач к простейшему варианту, основанному на понятии пропорции.

         Пусть требуется приготовить раствор определенной концентрации. В нашем распоряжении имеется два раствора: один с более высокой, чем требуемая, другой с менее высокой концентрацией, чем нужно.

         Если обозначить массу первого раствора через m₁, а второго – через m₂, то при смешивании общая масса смеси будет складываться из суммы этих масс: m₁+m₂.

         Пусть массовая доля растворённого вещества в первом растворе – q₁, во втором – q₂, а в их смеси – q.

         При решении задач на сплавы-смеси мы обычно составляем таблицу и пользуемся ею для получения уравнения или системы уравнений. Сделаем так и в этот раз:

 

	Масса раствора	Массовая доля вещества в растворе	Процентное содержание вещества в растворе
I раствор или сплав	m1	q1	q1*100	m1* q1
II раствор или сплав	m2	q2	q2*100	m2* q2
Смесь	m1+m2	q		m1* q1+ m2* q2

         Тогда общая масса растворённого вещества в смеси будет складываться из масс растворённого вещества в исходных растворах:

m₁* q₁+ m₂* q₂= (m₁+m₂)*q  или m₁* (q- q₁) = m₂*(q- q₂)

         Далее находим отношение масс:

          Очевидно, что отношение массы первого раствора к массе второго раствора есть отношение разности массовых долей растворённого вещества в смеси и во втором растворе к разности соответствующих величин в первом растворе и в смеси.

         При решении задач на растворы с разными концентрациями чаще всего применяют диагональную схему правила смешения, или квадрат Пирсона.

         При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение.

         Эти разности и показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.

         Задача 3.1. В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

         Решение. Делаем такой рисунок: в первой строке концентрация первого раствора, а под ней – второго. Посередине, между известными концентрациями растворов, расположим неизвестную нам концентрацию смеси, обозначив ее за x. Теперь проводим стрелки, как показано на рисунке, и на конце стрелок записываем разности. При записи разностей правило простое: надо вычитать из большего меньшее. В конце каждой строчки впишем массу растворов 1 и 2.

Концентрации исходных растворов	Концентрация смеси	Разности концентраций	Массы
12%		х%	5 кг
	х%
0%		12-х%	7 кг

Чтобы составить пропорцию, надо провести черточки дробей и поставить знак равно.

  Решаем пропорцию  .

Ответ: концентрация смеси равна 5%.

         Задача 3.2. Смешали некоторое количество 15% раствора некоторого вещества с таким же количеством 19% раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Решение.

Концентрации исходных растворов	Концентрация смеси	Разности концентраций	Массы
15%		19 – х %	m кг
	х%
19%		х – 15 %	m кг

 

         Снова записываем концентрации растворов 1 и 2 друг под другом, затем правее посередине неизвестную нам концентрацию смеси (х), а дальше проводим стрелки и записываем разности концентраций, только не забываем: надо вычитать из большего меньшее. Концентрация смеси никак не может быть больше 19 %, и не может быть меньше 15 %. То есть х>15 и x<19, следовательно, первая разность будет 19 - x, а вторая  – x – 15 (вычли из большего меньшее).

         Составим пропорцию .

 Ответ: концентрация смеси равна 17%.

         Задача 3.3. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Решение. Проделываем все те же операции, и снова составляем пропорцию.

Концентрации исходных растворов	Концентрация смеси	Разности концентраций	Массы
10%		5%	m1 кг
	25%
30%		15%	m2 кг

 

Известно также, что , поэтому

Тогда m₂=150 и масса первого меньше массы второго на 100 кг.

Ответ: 100 кг.

Задача 3.4. Сколько частей девяти процентного и семидесяти процентного уксуса надо взять, чтобы получить тридцати процентный раствор.

Решение.

Строим квадрат Пирсона.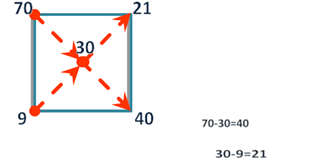

Ответ. 40 частей 9% уксуса, 21 часть 40% уксуса

3.4. Решение задач методом рыбки (старинным способом)

         Данный способ позволяет получить правильный ответ за очень короткое время и с минимальными усилиями. Впервые в России такой способ решения задач был описан в арифметике 18 века, автором которой был замечательный русский математик и педагог Леонтий Филиппович Магницкий. При решении задач этим способом строится схема, похожая на рыбку, вот поэтому он так и называется. Метод состоит в следующем: друг под другом записываем содержания веществ имеющихся растворов (смесей, сплавов), слева от них и примерно посередине - содержание вещества в растворе (в смеси или в сплаве), который должен получиться после смешивания. Соединяем написанные числа прямыми. В каждой паре из большего числа вычитаем меньшее, и результат записываем в конце соответствующей прямой. Получаемые массовые доли показывают, в каком отношении надо слить исходные растворы (смеси, сплавы). Записываем пропорцию и решаем её.

         Задача 4.1. Имеется два сплава меди и олова. Один сплав содержит 72% меди, а другой 80% меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75% меди?

         Решение. Друг под другом пишутся процентные содержания меди в имеющихся сплавах, слева от них и примерно посередине – процентное содержание меди в сплаве, который должен получиться после сплавления. Соединив написанные числа черточками, получим такую схему:

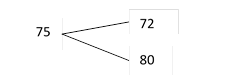
         Рассмотрим пары 75 и 72; 75 и 80. В каждой паре из большего числа вычтем меньшее, и результат запишем в конце соответствующей стрелочки. Получится такая схема:

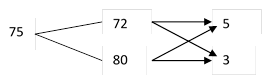
         Из нее делается заключение, что 72% сплава следует взять 5 частей, а 80% – 3 части (800:(5 + 3) = 100 г приходится на одну часть.) Таким образом, для получения 800 г 75% сплава нужно взять 72% сплава 100·5 = 500 г, а 80% – 100·3 = 300 г.

Ответ: 500 г, 300 г. 

 

Задача 5. Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35%, а во втором 60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?

 

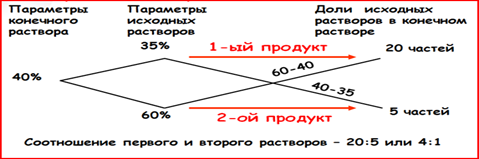
Ответ: 20:5 или 4:1.

 

3.5. Решение задач методом площадей равновеликих прямоугольников и подобия прямоугольных треугольников

         В тех задачах, где одна из рассматриваемых величин является произведением двух других, целесообразно для наглядности представлять такое произведение в виде площади прямоугольника. Для решения задач необходимо построить диаграмму по заданному условию. В горизонтальном направлении откладываем массу сплава (раствора, смеси), а в вертикальном — концентрацию сплава (раствора, смеси) или число долей вещества в сплаве. Получаем равновеликие прямоугольники, составляем уравнение, приравняв их площади.

Задача 5.1. Смешали 30% раствор соляной кислоты с 10% раствором и получили 600 г 15% раствора. На сколь­ко ­грам­мов масса пер­во­го рас­тво­ра мень­ше массы вто­ро­го?

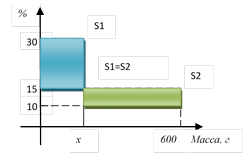Решение. Рассмотрим прямоугольники с площадями S1 и S2. Прямоугольники равновелики, так как количество соляной кислоты в обоих растворах после смешивания одинаково (масса смеси, умноженная на концентрацию равна количеству чистого вещества.)

Приравняв площади, равновеликих прямоугольников получаем

15x = 5 (600- x)

x = 150

600 – 150 = 450 г

450 - 150 = 300 (г)

Ответ: на 300 г.

Задача 5.2. При смешивании 5% и 40% растворов кислоты получили 140 г 30% раствора кислоты. Сколько грамм каждого раствора было взято?

Решение: через подобие прямоугольных треугольников.

Прямоугольные треугольники подобны. Запишем равенство отношений соответствующих сторон, подставив значения: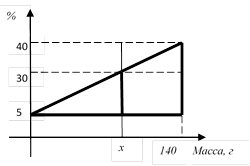

 

 

Ответ: 40 г 5%, 100 г 40%.

 

 

 

 

 

 

 

 

III. Анкетирование учащихся

Среди учащихся 9,10,11 классов нашей школы мы провели анкетирование по трём вопросам (Приложение 1). В данном опросе приняли участие 54 человека.

Вывод: из таблицы видно, что задачи по данной теме ученики решают чаще на уроках химии. Большая часть учащихся испытывает затруднения при решении задач на смеси, растворы и сплавы. Мало кто знает рациональные и нестандартные способы решения подобных задач и поэтому при решении таких задач на ЕГЭ и ГИА выпускники могут потерять «драгоценное» для себя время и баллы.

IV. Заключение

В ходе написания работы мной были использованы несколько источников информации: учебные пособия по математике и сборники задач для подготовки к экзаменам. Условия рассмотренных в работе задач были взяты из соответствующих теме разделов задачников по математике. Также в целях дальнейшего практического применения выводов работы мной были рассмотрены задачи из открытого банка заданий ЕГЭ по математике.

Моя гипотеза подтвердилась. Проведенное анкетирование, показало, что большая часть учащихся 9,10,11-х классов испытывает затруднения при решении задач на смеси, растворы и сплавы. Мало кто знает рациональные и нестандартные способы решения подобных задач.

В своей исследовательской работе я рассмотрела способы и методы решений задач на сплавы, смеси и растворы:

·        Табличный способ

·        Метод чаш 

·        Правило креста или метод Пирсона

·        Метод рыбки (старинный способ)   

·        Метод площадей равновеликих прямоугольников и подобия прямоугольных треугольников     

 Какие-то из них могут показаться легче, какие-то сложнее, но в целом их принцип очень похож. На уроках математики мы встречались с табличным способом при решении текстовых задач. Одним из преимуществ метода Пирсона является то, что он доступен ученикам, которые не умеют решать уравнения. Недостатком этого метода является то, что его можно применять только при смешивании двух растворов (сплавов). Правило креста имеет ту же сущность, что и старинный метод, но немного видоизменен и, как мне кажется, удобен. В каждой задаче половину успеха решает правильно составленное условие. В процессе решения задач выяснила, что таблицы, схемы, рисунки позволяют точнее, быстрее и проще составлять уравнения и системы уравнений к задачам, при этом вычислительный процесс не столь сложен. Работа имеет практическое значение, так как может служить пособием при подготовке к итоговой аттестации выпускников 9 и 11 классов.

В заключении важно отметить, что знание нескольких различных способов и дополнительная работа по выработке и развитию умений и навыков решения задач  позволит многим учащимся справиться с такими заданиями на экзамене намного быстрее и качественнее, так как будет возможность перепроверить себя, решая задачу другим методом.

Чтобы моим сверстникам и другим учащимся было легче ориентироваться в выборе наилучшего метода решения при разборе задач на смеси, мной был составлен буклет по методам  решения таких типовых задач, где для каждого отдельного метода отражен основной алгоритм решения.

           Свое выступления, мне хотелось бы закончить словами венгерского, швейцарского и американского математика Дьёрдь Пайо: «Решать задачи - такое же практическое искусство, как умение плавать или бегать на лыжах. Ему можно научиться только путем подражания или упражнения. Если Вы хотите научится плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. Лучший способ изучит что-либо – это открыть самому. Трудность решения в какой-то мере входит в само понятие задачи: там, где нет трудности, нет и задач»

 

 

 

 

 

 

 

 

V. Литература

1.     Лурье М.В., Александров Б.И. Задачи на составление уравнений. Учебное руководство. – М.: Наука. Главная редакция физико-математической литературы, 1990г.

2.     Шевкин А.В. Текстовые задачи: 7 – 11 классы: Учебное пособие по математике. – М.: «ТИД «Русское слово – РС», 2003. – 184 с.

3.     Шевкин А.В. Текстовые задачи в школьном курсе математики. М.: Педагогический университет «Первое сентября», 2006.

4.     Прокопенко Н.И. Задачи на смеси и сплавы. – М.: Чистые пруды, 2010 (Библиотечка «Первое сентября», выпуск 31).

Интернет –ресурсы:

1.     Решу ЕГЭ. Образовательный портал для подготовки к экзаменам. http://reshuege.ru/test?theme=88

2.     Федеральный институт педагогических измерений http://www.fipi.ru

3.     Сайт учителя математики http://www.shevkin.ru/

4.     Метод Пирсона в решении задач на сплавы и смеси https://easy-physic.ru

 

 

 

 

 

 

 

 

 

Приложение 1

Анкета для учащихся

 

 

 

Скачано с www.znanio.ru