Рациональные способы решения задач на смеси, растворы и сплавы

Алгоритм решения задачи на смеси, растворы и сплавы:

• изучить условие задачи;
• выбрать неизвестную величину (обозначить ее буквой);
• определить все взаимосвязи между данными величинами;
• составить математическую модель задачи (выбрать способ решения задачи, составить пропорцию или уравнение относительно неизвестной величины) и решить ее;
• провести анализ результата.

Табличный способ

При решении задач рассматриваемого вида, удобно использовать таблицу

                      Метод чаш

Метод состоит в следующем: необходимо изобразить каждый сплав (раствор, смесь) в виде прямоугольника. После заполняем получившиеся прямоугольники в соответствии с условием задачи.

Правило креста или метод Пирсона

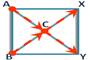
1. Строится квадрат, и проводятся его диагонали.

2. В левом верхнем углу ставят больший показатель крепости веществ (А).

3. В левом нижнем углу ставят меньший показатель крепости веществ (В).

4. На пересечении диагоналей ставят требуемый показатель крепости (С).

5. В правом нижнем углу после вычитания из А С получают У.

6. В правом верхнем углу после вычитания из С В получают Х.

7. Следовательно, чтобы получить смесь с концентрацией С нам надо взять Х частей с концентрацией А  и У частей с концентрацией В

Задача 3. Сколько частей девяти процентного и семидесяти процентного уксуса надо взять, чтобы получить тридцати процентный  раствор.

Решение. Строим квадрат Пирсона. Из большего отнимаем меньшее

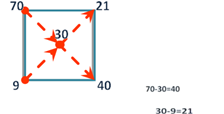
Ответ. 40 частей 9% уксуса, 21 часть 40% уксуса

Метод рыбки (старинный способ)

Метод площадей равновеликих прямоугольников и подобия прямоугольных треугольников

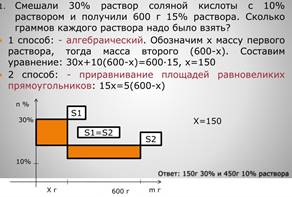
Для решения задач по данному методу необходимо построить диаграмму по заданному условию. В горизонтальном направлении откладываем массу сплава (раствора, смеси), а в вертикальном — концентрацию сплава (раствора, смеси) или число долей вещества в сплаве. Получаем равновеликие прямоугольники, составляем уравнение, приравняв их площади.

Скачано с www.znanio.ru