Рациональные вычисления при использовании теоремы Пифагора

Рациональные вычисления при использовании теоремы Пифагора.

Ни для кого не секрет, что теорему Пифагора мы используем не просто часто, а очень часто. И очень обидно, работая с учениками других школ, даже других городов, что используют они ее, как я называю c «прямотой телеграфного столба». Чем же можно помочь детям?

1)   Это небезызвестные треугольники с углами   Я считаю это находкой для решения многих задач в планиметрии и стереометрии.

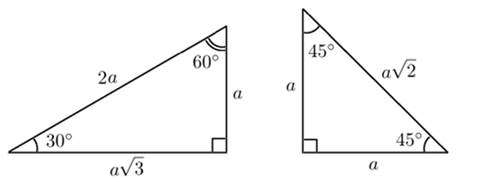
Массу задач можно решить практически устно, если видеть в треугольниках эти «говорящие» углы.

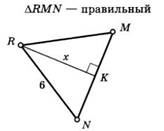
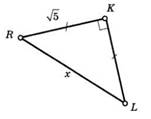
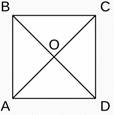
Пример 1. (задачи на готовых чертежах «Школа Пифагора»)

.                   

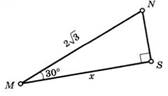
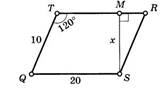
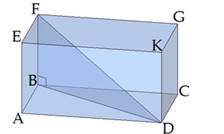
Пример 2. (задача c платформы якласс)

Диагональ прямоугольного параллелепипеда с плоскостью основания образует угол , стороны основания равны  и .

            Вычисли высоту параллелепипеда.

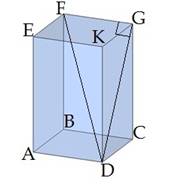
Пример 3. (задача из учебника Геометрия 10-11, Л.С. Атанасян )

Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в . Найдите угол между диагональю и плоскостью основания.

2)      Упрощение счета при прямом использовании теоремы Пифагора.

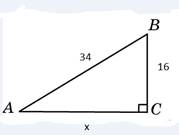
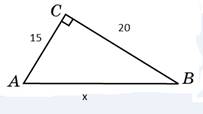
Сердце кровью обливается, когда дети начинают возводить числа в квадрат, складывать (вычитать) и извлекать квадратный корень. А ведь все так просто!

В первой задаче разделим числа на 2 (временно). Получим числа 8 и 17. Используя пифагорову тройку 8,15,17 получим катет, равный 15. И не забудем обратно умножить на 2. Ответ: 30.

Во второй задаче аналогично разделим числа на 5 (временно). Получим числа 3 и 4.  Используя пифагорову тройку 3,4,5 получим гипотенузу, равную 5. И не забудем обратно умножить на 5. Ответ: 25.

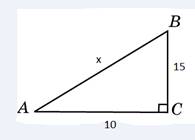
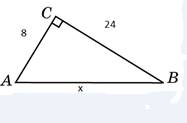
                    Разделим на 8. Получим числа 1 и 3.

                      . Умножим на 8. теорему Пифагора.                                                         Ответ:

  Умножим на 5.

Этот же принцип можно использовать при нахождении длины вектора. Ведь там тоже используется, по сути, теорема Пифагора.

Задание: найти длины векторов:

.

В первом случае разделим на 2. Получим числа 20 и 21 (минусом можно в этом случае пренебречь, т.к. при возведении в квадрат они все равно исчезнут). Используем пифагорову тройку: 20,21,29. Умножим на 2. Ответ: 58.

Во втором случае делим на 7. Получим числа 1 и 4. Используем теорему Пифагора для этих чисел:  . Умножим на 7.  Ответ: .