
Рациональные вычисления в теме «Дробные выражения».
При изучении темы «Дробные выражения» впервые появляется возможность избавляться от запятых в десятичных дробях и работать с «многоэтажными» дробями.
Хочется поделиться тем, как я учу этому своих учеников и где это можно использовать.
Пример 1.
![]()
Так как в обеих частях дробей есть только действие умножение и после запятых в числителе и знаменателе одинаковое количество цифр, то можно обе части дроби умножить на 1000, т.е. избавиться от запятых. После чего можно выполнить сокращение.
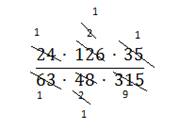 Ответ:
Ответ:
![]()
Пример 2.
![]()
Так как количество цифр после запятой в числителе и знаменателе дроби разное, то придется дописать 2 нуля к числам в знаменателе.
Это может быть, например, такой вариант.
![]()
Выполним сокращение: 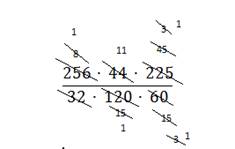
Ответ: 11
Пример 3.
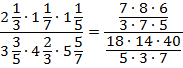
Выполним сокращение. Можно сокращать или через этаж, или 1-2 и 3-4 этажи между собой.
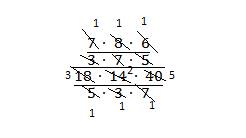
Не забудем, что при делении дроби на дробь вторая дробь переворачивается.
![]()
Ответ: ![]()
Пример 4.
Указанные преобразования можно использовать при решении уравнений на пропорции.
Решить уравнение:
![]()
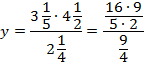
Выполним сокращение:
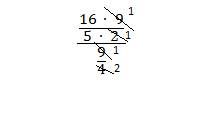
![]()
«Четырехэтажные» дроби можно использовать при нахождении суммы первых членов геометрической прогрессии.
Пример 5.
Найти сумму первых шести
членов геометрической прогрессии ![]() , у которой
, у которой ![]()
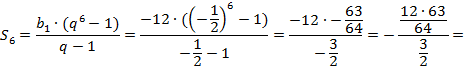
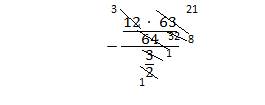
![]()
Ответ: -7,875
Замечание: С «трехэтажными» дробями работать надо очень аккуратно. В 6 классе полезно превращать их в «четырехэтажные», на мой взгляд.
Пример 6.
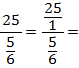
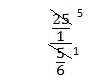
![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.