Практическая работа № 31.

Тема: Алгоритмизация.

Наименование: Разработка алгоритмов с циклической структурой.

Цель работы: Ознакомить с различными способами записи алгоритма и видами алгоритмов. Научить составлять алгоритмы с циклической структурой.

1. Краткие теоретические сведения.

Существует широкий круг задач, при решении которых необходимо повторять неоднократно совокупность действий. Процесс решения таких задач описывается алгоритмом, тип  которого определяется как циклический.

Циклическими называются такие алгоритмы, в которых получение результата обеспечивается многократным выполнением одних и тех же операций.

Совокупность повторяющихся действий называется телом цикла.

Основные разновидности циклов представлены в таблице:

Таблица 1

нц пока условие

   тело цикла

   (последовательность действий)

нц 

   тело цикла

  (последовательность действий)

нц для i от N до K с шагом S

   тело цикла

   (последовательность действий)

кц

Примеры структуры цикл                               Таблица 2

нц пока i <= 5

   S := S+A[i]

   i := i+1

N:=3

нц

K:=N^2

N:=N+2

до N>5

кц

нц для i от 1 до 5

   X[i] := i*i*i

   Y[i] := X[i]/2

кц

Задача 1: Составить алгоритм вычисления суммы 100 первых натуральных чисел.

Запишем алгоритм на алгоритмическом языке.

алг Сумма (цел i, S)

       арг i

       рез S

нач

i:=1

S:=0

нц пока i £ 100,

S:=S + i

i:=i + 1

кц

кон

Составим графическую форму:

Задача 2: Составить алгоритм вычисления значений функции y=x²-3x  для х от 0 до 10 с шагом 0,5

Запишем алгоритм на алгоритмическом языке.

алг Функция (вещ x, y)

       арг x

       рез y

нач

нц для x от 0 до 10 с шагом 0,5

y:= x^2 – 3x

кц

кон

Составим графическую форму:

2. Задания.

1. Внимательно изучите теоретический материал.

2. Определите в данных условиях цикл и определите: начальное значение, конечное значение, шаг

а) 1, 2, 3, 4, ... ,10.

б) -5, -4, -3, -2, ... , 5.

в) 2, 4, 6, ... , 20.

3. Какие значения будет принимать величина-счетчик при выполнении следующих циклов?

а) от x=7 до 10 шаг 1;

б) от b=1 до 13 шаг 4;

в) от c=30 до 10 шаг -5;

4. Определите по блок-схемам нижеприведенных структур, к какому виду циклов они относятся? Запишите данные структуры на алгоритмическом языке.

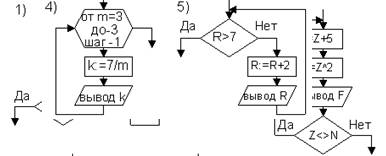5. Составьте блок-схему решения задач:

а) Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10% от нормы предыдущего дня. Сколько км пробежал спортсмен за каждый день недели?

б) На опытном лесном участке ежегодный прирост древесины - 10%. Какое количество ее будет через 6 лет, если в начале 1 года было посажено 20000 м³?

в) В банк был положен вклад в размере N руб. Каждый месяц он увеличивался на 1%. Определите размер вклада через 5 лет.

Вопросы:

1. В чем различие циклов до и пока ?

2. С каким шагом будет изменяться параметр цикла для, если не указан шаг изменения параметра?

3. Оформление отчета:

1. Переписать определение циклического алгоритма, типы структур цикл, таблицы 1 и 2  из методического пособия в тетрадь.

2. Выполнить п. 2, 3,4 и 5 задания.

3. Дать ответы на вопросы задания и объяснить их.

4. Контрольные вопросы.

1. Какие способы записи алгоритма вы знаете?

2. Как различаются циклические алгоритмы по структуре?

3. Какие типы алгоритмов вы знаете?