Поделиться
неизвестное количество.pdf
Ежедневно Малыш съедал одну конфету.
Каждое воскресенье к нему прилетал Карлсон, и Малыш угощал его парой конфет.
Сколько конфет съел Карлсон к моменту, когда конфеты закончились? (1 января 2010 года - пятница).
Анализируем:
Конфеты ели двое - Малыш и Карлсон. Вначале конфет было 313 штук. Малыш за неделю съедал 7 конфет (по одной в день), а Карлсон -всего две (по воскресеньям). Следовательно, за неделю они оба съедали 9 конфет.
Чтобы узнать, сколько конфет съел Карлсон, нужно знать, на сколько воскресений хватило конфет. А это можно узнать, зная сколько было конфет и сколько их съедали за неделю.
Решаем:
Малыш и Карлсон каждую неделю съедали по 9 конфет. Неполное частное от деления 313 на 9 равна 34, а остаток равен 7. Следовательно, конфет хватило на 34 недели и ещё на несколько дней. Так как эти несколько дней начинаются с пятницы и на них осталось 7 конфет, то ещё одно воскресенье Карлсон получал конфеты. Следовательно, он получал конфеты 35 воскресений и съел 35*2 = 70 конфет.
Ответ. 70 конфет.
Самостоятельно:
1) Сколько конфет съел Малыш?
2) На сколько дней хватило конфет?
3) В какой день недели была съедена последняя конфета?
4) Каким будет ответ, если Малыш будет давать Карлсону каждое воскресенье пять конфет?
5) Сколько конфет должно было быть вначале, чтобы при том же режиме их употребления их хватило бы до 1 января 2011 года?
Малыш и Карлсон принимали участие в легкоатлетическом забеге в
составе 10 друзей.
В некоторый момент оказалось, что трое впереди Малыша, а сзади Карлсона - четверо.
Сколько в этот момент человек находилось между Карлсоном и
Малышом, если никто из бегущих не находился рядом друг с другом?
Анализируем:
Чтобы подсчитать искомое количество участников забега, нужно рассмотреть два случая:
Малыш сзади Карлсона и Малыш впереди Карлсона.
И воспользоваться условием об их месте в забеге.
Это позволит ответить на поставленный вопрос
Если Малыш сзади Карлсона, то сзади Карлсона будут находиться Малыш и ещё 3 человека (4 человека сзади Карлсона).
Пусть Малыш бежит непосредственно за Карлсоном. Тогда впереди Малыша - Карлсон и ещё двое (впереди Малыша трое), между Малышом и Карлсоном - ни одного человека (см. рисунок).
Общее число участников забега будет равно 7, что противоречит условию. Этот случай невозможен.
Решаем: 
Пусть Карлсон сзади Малыша. Тогда сзади его будут находиться четверо друзей, впереди Малыша - трое.
Чтобы число участников забега равнялось 10, между ними должен стоять один человек (см. рисунок).
Ответ: Один.
Самостоятельно:
1) Каким будет ответ, если в забеге участвовало: а) 9 человек; б) 15 человек?
2) Каким будет ответ, если трое будут бежать впереди Карлсона, а четверо сзади Малыша?
3) Каким будет ответ, если впереди Малыша будут пятеро, а сзади Карлсона двое?
4) Сколько должно было бы бежать человек, чтобы выполнялись остальные условия задачи, но Малыш бежал сзади Карлсона?
Чтобы оградить участок квадратной формы, нужно вдоль каждой стороны установить по 8 столбов, причем, по одному в углах участка.
Сколько всего понадобится столбов?
Анализируем:
Изобразим участок в виде квадрата (см. рис. 6), чтобы удобнее
было рассуждать. Конечно, можно изобразить и столбы в соответствии с условием,
а потом подсчитать их.
Но столбов могло быть (в другой задаче) и по 80 на каждой стороне. И тогда непосредственный подсчёт был бы затруднительным.
Намного легче найти нужное количество столбов с помощью математических действий. Так как на каждой стороне участка 8 столбов и два из них на её концах, то между концами каждой стороны (между соседними вершинами квадрата!) стоит по 6 столбов. А кроме того, 4 столба стоят по углам участка.
Из условия следует, что между концами каждой стороны участка должно стоять по 6 столбов Сторон всего 4.
 |
По углам участка должны стоять столбы.
Значит, требуется ещё 4 столба. Всего нужно 24 + 4 = 28 столбов.
Ответ. 28 столбов.
Самостоятельно:
1) Сколько потребуется столбов, если вдоль каждой стороны должно стоять 20 столбов?
2) Сколько потребуется столбов, если длина участка 100 метров и столбы должны стоять на расстоянии 2 метра друг от друга?
3) Сколько столбов ставили на каждой стороне участка, если всего поставили 60 столбов?
4) Какова длина участка, если всего поставили 120 столбов через каждые 3 метра?
Сколько книг приобрели по каждому предмету, если книг по информатике купили больше, чем по истории, а по математике - меньше, чем по истории?
Анализируем:
Из условия задачи вытекает, что купили различное число книг по каждому из трёх предметов, больше всего по информатике, меньше всего по математике.
Для решения задачи число 7 нужно представить в виде суммы трёх различных натуральных чисел.
Решаем:
Так как число 7 единственным образом можно представить в виде суммы трёх различных натуральных чисел: 7 = 1 + 2 + 4, то больше всего купили книг по информатике - 4, по истории 2 и одну по математике.
Ответ. Купили одну книгу по математике, 2 - по истории, 4 - по информатике.
Самостоятельно:
1) Сколько могло бы быть вариантов покупки, если бы купили: а) 8 книг; б) 9 книг?
2) Сколько могло бы быть вариантов покупки, если бы не было условия: по математике купили книг меньше, чем по истории?
3) Сколько могло бы быть вариантов покупки, если бы не было условия: по информатике купили книг больше, чем по истории?
Бревно перепиливается за 1 мин.
Надо напилить 20 столбиков длиной 1 м.
Можно пилить только 4-метровые или только 5-метровые брёвна.
Какие брёвна надо пилить, чтобы выполнить работу за кратчайшее время?
Анализируем
Чтобы, например, из 4-метрового бревна получить 4 столбика длиной 1 м, нужно сделать три распила, на 1 меньше, чем число столбиков: ведь последний распил даёт 2 столбика.
По условию можно для каждого вида брёвен определить то их
количество, которое предстоит распилить (это частное от деления числа
необходимых столбиков на длину ребра).
Потом можно найти количество распилов, которое предстоит сделать (это произведение числа распилов для одного бревна на число брёвен) и время, необходимое для работы (на один распил требуется 1 мин).
Решаем:
Пусть перепиливают 4-метровые брёвна.
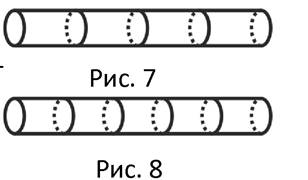
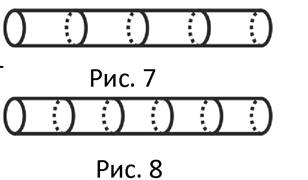
Одно бревно даёт 4 метровых столбика при трёх распилах (см. рис. 7). Чтобы получить 20 метровых поленьев, надо взять 20:4 = 5 брёвен и сделать 3*5 = 15 распилов. Для этого потребуется 1*15 = 15 мин.
Пусть перепиливают 5-метровые брёвна.
Одно бревно даёт 5 метровых столбиков при четырёх распилах (см.рис. 8). Чтобы получить 20 метровых столбиков, надо взять 20:5 = 4 бревна и сделать 4*4 = 16 распилов. Для этого потребуется 1*16 = 16 мин.
Так как 15 мин меньше 16 мин, то пилить надо 4-метровые брёвна.
Ответ. 4-метровые бревна.
1) Сколько потребуется распилов, чтобы 4-метровое бревно распилить на полуметровые чурбаки?
2) Сколько из 4-метрового бревна получится полуметровых чурбаков?
3) Нельзя ли уменьшить время выполнения указанной работы, распиливая брёвна разной длины?
Чтобы подняться с первого этажа на третий этаж дома, надо пройти 48 ступенек.
Сколько ступенек надо пройти, чтобы подняться на
шестой этаж этого дома?
Количество ступенек между этажами одинаковое.
Подняться на третий этаж - это значит преодолеть два этажа: с первого на второй и со второго на третий, то есть на один меньше номера этажа.
Пользуясь этим, можем определить, сколько надо пройти ступенек, чтобы подняться на один этаж.
(Количество ступенек между этажами одинаковое!)
Далее можно найти, сколько этажей надо преодолеть, чтобы подняться на шестой этаж и сколько пройти при этом ступенек.
Чтобы преодолеть один этаж, нужно пройти 48:2 = 24 ступеньки.
Чтобы подняться на шестой этаж, надо преодолеть 6 - 1 = 5 этажей и при этом пройти 24*5 = 120 ступенек.
Ответ: 120 ступенек.
Самостоятельно:
1) Сколько этажей надо преодолеть, чтобы подняться на четвёртый этаж?
2) Сколько ступенек надо пройти, чтобы подняться на пятый этаж?
3) Во сколько раз больше надо пройти ступенек, чтобы подняться на седьмой этаж, чем на четвёртый?
Проверь себя:
Задача 1. На токарном станке вытачивают детали из заготовок: из одной заготовки - одну деталь.
Из стружки, которая образовалась после изготовления шести деталей, можно выплавить еще одну заготовку.
Сколько деталей можно получить из 64 заготовок, если стружку переправлять в заготовки?
А. 64. Б. 74. В. 76. Г. 77.
Проверь себя:
Задача 2. Моя остановка трамвая седьмая от одного конца маршрута, и двенадцатая - от другого конца. Сколько на этом маршруте всего остановок?
А. 17. Б. 18. В. 19. Г. 20.
Задача 3. Длина забора 20 метров. Сколько в заборе столбов, если столб от столба стоит на расстоянии двух метров? А. 9. Б. 10. В. 11. Г. 19.
Проверь себя:
Задача 4. Лена, Оля и Таня втроём участвовали в беге на 100 м. Лена прибежала к финишу на 2 с раньше Оли, а Оля - на 1 с позже Тани.
Кто прибежал последним и на сколько секунд он отстал от предпоследнего?
А. Таня, на 1 с. Б. Таня, на 2 с.
В. Оля, на 2 с. Г. Оля, на 1 с.
Проверь себя:
Задача 5. Мама дала Вере несколько верёвок и поручила ей нарезать маленькие верёвочки для завязывания мешков.
Спустя некоторое время Вера подсчитала, что она сделала 12
разрезов и получила 19 маленьких завязок.
Сколько верёвок разрезала Вера?
А. 5 Б. 6 В. 7. Г. Определить невозможно.
Проверь себя:
Задача 6. Таня живёт на 2-м этаже. Ваня в том же подъезде, но ему приходится подниматься по лестнице, в которой в 2 раза больше ступенек.
Ступенек до подъезда и до 1-го этажа нет.
На каком этаже живёт Ваня?
А. На 3-м Б. На 4-м. В. На 6-м.
Г. Определить невозможно
Молодцы!
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
