Разработка открытого урока алгебры: "Свойства определённого интеграла"

Урок алгебры на тему:

11 класс

Цели  урока:

Учебные: 1)  изучение основных свойств определенного интеграла.

2) Развивать культуру устного вычисления определенных интегралов.

3) Содействовать развитию у учащихся умений осуществлять самоконтроль, самооценку.

Развивающие: Развивать мышление и речь учащихся, развивать навыки самостоятельного мышления, интеллектуальные навыки (анализ, синтез, сравнение, сопоставление), внимание, память.

Воспитательная: Содействовать воспитанию интереса к математике, активности, мобильности, аккуратности  и  внимательности.

Задачи урока:

1.Развитие познавательного интереса к предмету.

2.Воспитание самостоятельности, настойчивости  при достижении конечного результата.

3.Формирование культуры учебной деятельности и информационной культуры.

Тип урока: комбинированный.

Методы обучения: фронтальный, индивидуальный, наглядно-практический.

Формы организации взаимодействия на уроке: учебная, групповая работа, индивидуальная работа.

Оборудование и наглядные средства обучения:  учебник, ноутбук, проектор,   демонстрационный и раздаточный материал.

Ход урока

1.Организационный момент.

Подготовка учащихся к уроку (проверка отсутствующих на уроке, наличие тетрадей, учебников)

2. Актуализация опорных знаний.

1)Учитель. Давайте повторим первообразные некоторых элементарных функций.

2)Учитель.

А теперь вспомним правила нахождения первообразных и формулу Ньютона-Лейбница.

3)Учитель.

Сейчас 4 ученика выполнят тест на время. 30 секунд на обдумывание.

Ответы писать на листах теста.Тест

1. Если для любого х из множества Х выполняется равенство F'(x)=f(x), то функцию F(x) называют … для функции f(x) на данном множестве:

А) производной

В) первообразной

С) обратной

Д) непрерывной

2. С помощью формулы Ньютона-Лейбница находят…

А) определенный интеграл

В) производную

С) обратную функцию

Д) неопределенный интеграл

3. Найдите множество первообразных для функции f(x)=2

А) 0

В) 2х+с

С) 2х

Д)  2

4. Разность F(b)-F(a) называют … от функции f(x) на отрезке [a; b]

А) производной

В) интегралом

С) первообразной

Д) обратной функцией

5. Совокупность всех первообразных функций F(x)+с для данной функции f(x) называется … функции f(x)

А) область определения

В) производная

С) область значений

Д) неопределенный интеграл.

Ответы для взаимопроверки:

В это время ученики устно выполняют следующие задания.

Устная работа: (задания записаны на доске; цена ответа 1 балл)

1) Исправить ошибки в записи    ; 

 Ответ: ( 2x  + C)

 .        

 Ответ: (– 5x  +  C)

2) Найти интеграл:dx;             

Ответ:  (

      ;             

Ответ: (  + C = - 

  .          

Ответ: ( 5 ln │x│)

3) Вычислить:  ;          

Ответ: (1)

Ответ: ( sinπ  -  sin0  = 0 ).

4)Обобщение  (презентация).

К понятию определенного интеграла приводит задача нахождения площади криволинейной трапеции.

Пусть на некотором интервале [a,b] задана непрерывная функция

            Задача:           

            Построить ее график и найти S площадь фигуры, ограниченной этой кривой, двумя прямыми x = a и x = b, а снизу – отрезком оси абсцисс между точками x = a и x = b.

Фигура aABb называется криволинейной трапецией

Под определенным интегралом                                            

от данной непрерывной функции f(x) на данном отрезке [a;b] понимается соответствующее приращение ее первообразной.

Числа a и b – пределы интегрирования, [a;b] – промежуток интегрирования.

3. Изучение нового материала.

Работа с учебником. Стр. 191-192, п.6.7.

Рассмотреть основные свойства.

Разобрать, что означает каждое свойство.

Рассмотреть примеры применения свойств.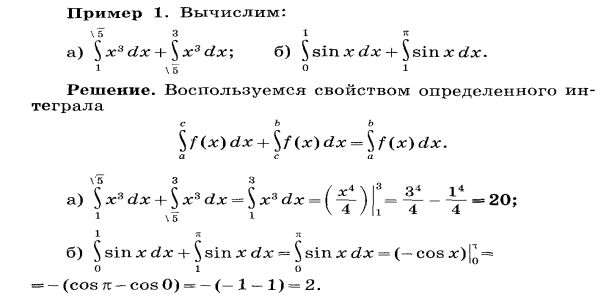

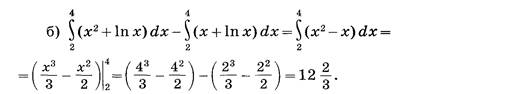
4.Закрепление знаний.

Учитель. Давайте решим следующие задания: 

(Двое учащихся выполняют задания за закрытой доской, с последующей проверкой)

Задание 1. Найдите определенные интегралы:

1) 2)   3)  4)

Ответы: 1);  2);  3)  4)

Задание 2.(Самостоятельное решение с последующей взаимопроверкой)

Найдите определенные интегралы:

1) + 5)dx;  2) 3);  4)

Ответы: 1) 2)   3)  4)

5.Домашнее задание.

п. 6.7 выучить основные свойства, № 6.64(а,б), 6.65(в), 6.66(б,г)

6.Подведение итогов.

Какие вычисления мы производили сегодня на уроке?

 Рефлексия деятельности учеников на уроке.

-Что понравилось на уроке?

-Какой материал был наиболее интересен?

-Оцените свою работу на уроке: плохо работал, хорошо, отлично. Поднимите   руки, кто работал плохо? Почему? И т.д.

Выставление оценок.