Разработка урока по алгебре "Построение графика квадратичной функции"

Тема: «Построение графика квадратичной функции»

Цель:

Образовательная:

- проверить знания и умения учащихся по предыдущей теме "Преобразование графика  y= ax²;

- сформулировать с учащимися алгоритм построения графика квадратичной функции;

- первичное закрепление умений и навыков учащихся по теме.

Развивающая:

- продолжать формировать общие учебные умения и навыки;

- развивать  навыки работы по алгоритму, навыки самостоятельной работы;

- развивать логическое мышление;

- развивать познавательный интерес к предмету.

Воспитывающая:

- воспитывать внимательность, аккуратность, ответственность.

Задачи урока: познакомить учащихся с построением графика квадратичной функции.

Средства обучения: проектор, презентация, раздточный материал.

Тип урока: комбинированный.

Ход урока.

I.                Организационный этап (приветствие, проверка готовности к уроку).

II.        Всесторонняя проверка знаний. Фронтальный опрос.

1.     По графику определить координаты вершины параболы, ось симметрии.

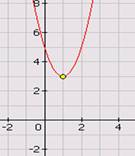
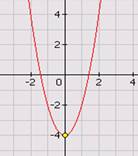
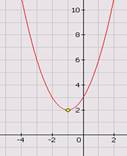
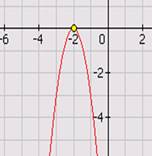
2.     Установите соответствие между графиком функции формулой и координатами вершины параболы.

А)                               Б)                                              А)             Б) 

III.        Подготовка учащихся к активному усвоению нового материала.

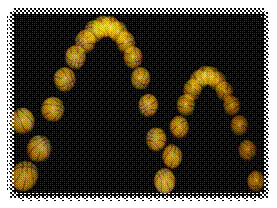
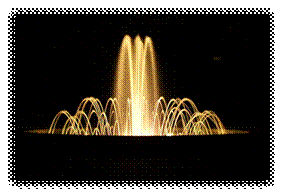
Опираясь на ранее изученный материал определить, по какому признаку можно объединить следующие рисунки

IV.       Изучение нового материала:

ü тема урока сообщается после совместных выводов полученных при просмотре слайдов;

ü озвучиваются  цели и задачи изучения нового материала, мотивация учащихся к его освоению.

Дается определение квадратичной функции.

 Определение:  квадратичной функцией называется функция, которую можно задать формулой вида  y = ax²  +  bx+ c, где х – независимая переменная, a, b и с – некоторые числа (причем, а ≠ 0).

 Назовите коэффициенты данных квадратичных функций.

 Например:

- у = 5х² + 6х+ 3,     a = 5,    b = 6,  c = 3

- у = – 7х²+8х – 2,   a = -7,   b = 8,  c = -2

- у = 0,8х² + 5,         a = 0.8,  b = 0,  c = 5

- у = х² – 8х,             a = ¾,    b = -8,  c = 0

- у = – 12х²               a = -12,  b = 0,  c = 0

        Дается определение графика квадратичной функции.

Определение: графиком квадратичной функции является парабола, ветви которой направлены вверх (если а > 0) или вниз (если а < 0).

Приводятся примеры графиков квадратичной функции, акцентирующие внимание  на разное направления ветвей.

                                                     у = 2х² + 4х – 1 – графиком является

                                                      парабола, ветви которой направлены

                                                         вверх (т.к. а = 2, а > 0).

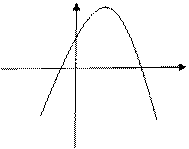
у= – 7х² – х + 3 – графиком является

 парабола, ветви которой направлены

вниз (т.к. а = -7, а < 0).

Для построения графика квадратичной функции удобно пользоваться определенным порядком действий, т.е. алгоритмом.

 Алгоритм  построения графика функции.

1)    Описать функцию:

¾   название функции, что является графиком функции

¾   направление  ветвей  параболы.

Пример: у = х²– 2х – 3 –графиком является парабола, ветви которой направлены вверх (т.к. а = 1, а > 0).

2)    Найти координаты вершины параболы А(;) по формулам:

=   и    = у ()  т.е. подставить найденное значение абсциссы  в формулу, которой задана функция и вычислить значение .

Определить ось симметрии х = .

Пример: у = х² – 2х – 3, (а = 1; b = – 2; с = – 3).

Найдем координаты вершины параболы:

,  т. А(1;-4) – вершина параболы.

Прямая  х = 1 – ось симметрии параболы (т.е. точки параболы находятся на одинаковом расстоянии от этой прямой слева и справа).

3)    Найти точки пересечения с осями координат.

 Если график пересекает ось ОХ, то у-я координата равна 0; если график пересекает ось ОУ, то х-я координата равна 0.

ОХ:  у = 0,   х² – 2х – 3 = 0,

                      .

ОУ: х = 0,    у = - 3

4)    Построить график функции: отметить в координатной плоскости вершину параболы, ось симметрии, точки пересечения с осями координат отобразив симметрично точку пересечения с осью ОУ, и соединить их плавной линией.

V.Первичное закрепление изученного материала

А) Построить, опираясь на алгоритм, график функции у = – х² + 4х – 3 и по графику определить область значений функции и промежуток убывания функции (задание 3.1,  ГИА вариант 25).

АЛГОРИТМ (у всех на парте):

1.     Описать функцию:

¾              что является графиком функции;

¾              куда направлены ветви параболы.

2.     Найти координаты вершины параболы т.А(; )

=   и    = у ()  .

3.     Найти точки пересечения с осями координат.

4.     Построить график функции.

Работа у доски:

у = – х² + 4х – 3 –графиком является парабола, ветви которой направлены вниз (т.к. а = - 1, а < 0);

Найдем координаты вершины параболы:

, т.А (2; 1) – вершина параболы.

х = 2 – ось симметрии параболы.

Найдем точки пересечения с осями координат:

ОХ: – х² + 4х – 3 = 0, найдем корни с помощью дискриминанта

D =  , ,

 .

ОУ: у = - 3. Отобразим симметрично х = 2 данную точку.

Соединив точки получим параболу по которой легко определить:

 Е (у): (-,  функция убывает, х.

Если вы допустили ошибку – не огорчайтесь! У вас все еще впереди!

Б) Перед продолжением работы запишите домашнее задание: повт. , выучить алгоритм наизусть построить график функции                                                                       у = - х² - 6х - 7   и   у = - х² +6х - 8

В) Работа в парах:

Выполните следующую работу в тетрадях (№ 3.1. ГИА в.24): постройте график  функции    у =  х² + 2х – 3 и по нему найдите область значений функции и промежуток возрастания функции.

Самопроверка:

у = х² + 2х – 3 –графиком является парабола, ветви которой направлены вверх (т.к. а =  1, а > 0);

Найдем координаты вершины параболы:

, т.А (-1;-4) – вершина параболы.

х = -1 – ось симметрии параболы.

Найдем точки пересечения с осями координат:

ОХ: х² + 2х – 3 = 0, найдем корни с помощью дискриминанта

D =  , ,

 .

ОУ: у = - 3. Отобразим симметрично х = 2 данную точку.

Соединив точки получим параболу по которой легко определить:

Е (у): , функция возрастает х.

VIІ.Выставление оценок, подведение итогов урока.

Сегодня на уроке мы познакомились  с алгоритмом построения графика квадратичной функции; рассмотрели примеры решения из сборника ГИА для 9 класса по математике.

VI. Рефлексия: оцените свое настроение и состояние на уроке по 5-ти бальной шкале: «5» - отличное, «4» - хорошее, «3» - нормальное, «2» - плохое, «1» - очень плохое.