Развитие функциональной грамотности обучающихся при изучении курса Вероятность и статистика

Развитие функциональной математической грамотности у обучающихся в ходе изучения учебного курса «Вероятность и статистика»

Петрова Н.В., учитель математики высшей категории

МКОУ Заволжского лицея

В школьной жизни часто случаются изменения: одни учебные курсы исчезают, другие добавляются. Теперь школьники изучают «Теорию вероятностей и статистику». Согласитесь, что учителя восприняли такое введение без особого энтузиазма. Почему?

Ведь это одна из возможностей в рамках отдельного курса, как это требуют обновленные ФГОС, «формирования функциональной грамотности обучающихся (способности решать учебные задачи и жизненные проблемные ситуации на основе сформированных предметных, метапредметных и универсальных способов деятельности), включающей овладение ключевыми компетенциями, составляющими основу дальнейшего успешного образования и ориентации в мире профессий.»

Важной особенностью преподавания курса "Вероятность и статистика" является его связь с реальными примерами и задачами. Учащиеся рассматривают различные ситуации из реальной жизни, в которых применяются принципы вероятности и статистики. Это позволяет им увидеть, как математика применима в различных областях науки, бизнеса и повседневной жизни, а также развивает их способность анализировать информацию и принимать обоснованные решения.

Если заглянуть в Примерную рабочую программу по математике, в раздел

«Вероятность и статистика», то вы увидим основные содержательные линии курса

В каждой из этих линий основное содержание направлено на решение именно практико-ориентированных задач, которые являются основным инструментом формирования математической грамотности обучающихся. 

Сделав первые шаги в преподавании нового предмета, решила найти ответ на вопрос, как эффективнее использовать возможности программного материала нового курса, в частности для развития функциональной грамотности, понять, в чем трудности преподавания теории вероятностей и статистики в средней школе, как найти пути их преодоления.

В нашей российской школе отсутствует традиция преподавания данного курса. С этим предметом не знакомы наши коллеги: ни мы, ни наши знакомые и друзья, ни наши ни их дети в школе его не изучали. Поэтому вокруг теории вероятностей, как любого новшества, возникает ореол настороженности. Нам приходится доказывать целесообразность изучения этого предмета. 

Ученики пока не понимают, что это такой же предмет, что и алгебра с геометрией, значит, к нему можно относиться как к второстепенному. Такова психология современного ученика, знающего, где нужно выкладываться по-настоящему, а где можно ослабить усилия.

Родители сетуют, что не могут помочь своим детям, переживают, не зная, к кому обратиться за помощью: «Раньше, если что, соседка помогала, но она сказала, что задачи по теории вероятностей решить не сможет...»

Другая, не менее острая, причина заключается в том, что на момент введения нового предмета среди учителей математики нет достаточного количества учителей, свободно владеющих содержанием курса статистики и теории вероятностей, решающих вероятностные задачи на том же уровне, что и задачи по алгебре. Учительская психология во многом похожа на детскую: что спросят, тому и будем учить! В 9-м классе экзамен, надо алгебру повторять, а я столько часов отдам на непонятно что? Да и своего времени жалко. Легче делать то, что давно хорошо получается, чем погружаться в новый раздел. (свое отступление о 9 классе)

По всем разделам школьной математики существуют учебно-методические комплекты в помощь педагогу. Методическая литература настолько разнообразна, что встает проблема отбора лучшего материала из предложенного. По теории вероятностей и статистике на сегодняшний день мы этим похвастаться не можем.

Подспорьем в этом нам выступают КИМ ВПР, ОГЭ. Продемонстрирую известные таблицы, диаграммы, логические упражнения.

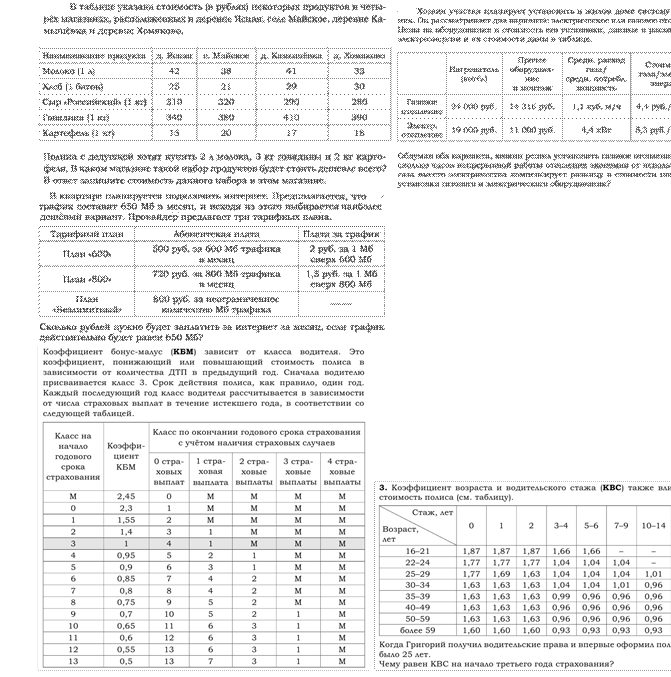
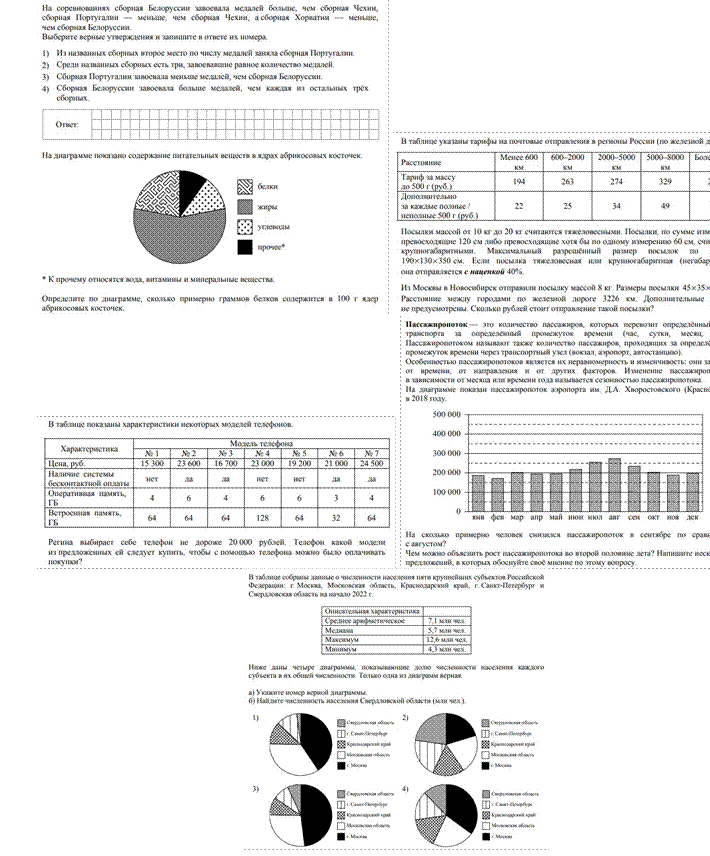
Неоспорим факт, что учитель математики должен «перевести» решение математической задачи на понятный слушателю язык, сделать мысль доступной пониманию многих, разложить все по полочкам. Учитель должен направить мысль ученика на поиск решения, а видя неверный ответ, найти дефект в рассуждениях, который привел к ошибке. Учитель знает много разных хитростей: мнемонические правила для запоминания, разделение задач на разные удобные для обучения виды, еще он знает, где в его науке хранятся ключевые идеи, которые упустить нельзя, потому что на них опирается дальнейшее обучение. 

Всё вышеназванное — есть методика преподавания предмета, то, что позволяет решить задачи современного образования, том числе и в вопросах функциональной грамотности. А перед многими из нас сейчас проблема - каждый педагог должен самостоятельно создавать эту методику методом проб и ошибок. А положительные результаты в обучении требуются сразу, в том числе на независимых проверках (ВПР, ОГЭ). 

Мы привыкли вести «письменный» предмет со всеми присущими ему чертами: серьезность, догматизм, многократный повтор одних и тех же алгоритмов. А на уроках по «Теории вероятностей» надо решить несколько задач, абсолютно непохожих друг на друга. Задачи, стоящие в учебнике рядом, не аналогичны, решение одной из них не означает, что будет с легкостью решена следующая! (Похожая ситуация часто встречается и в геометрии.)

Например, на уроке по теме «Элементарные события» сначала надо проявить комбинаторные навыки, чтобы расставить трех человек в очередь всеми возможными способами; в следующей — сообразить, что попадания в различные зоны мишени не связаны между собой; а решая задачу с подбрасыванием монеты, догадаться, что с увеличением числа попыток число событий будет увеличиваться в два раза. Хорошо бы потом увидеть, что первая задача не такая, как две последние, а две последние как раз очень похожи между собой. Но это уже опять мы возвращаемся к проблемам методики преподавания. 

Новый УМК Математика. Вероятность и статистика: 7-9-е классы: базовый уровень: учебник: в 2 частях Высоцкий И.Р., Ященко И.В.; под ред. Ященко И.В. (хотя УМК его в полном объеме назвать нельзя), в дополнение к учебнику издано только лишь Методическое пособие, в аннотации к которому написано, что в книге раскрываются содержательные и методические особенности курса, приводятся общие методические рекомендации. А все основное мы черпаем из проводимых вебинарах, семинарах, слушаем на курсах, на которых нас учат решать задачи (и это тоже немаловажно конечно), а вот приемы, методы, технологии формирования вероятностных и статистических понятий мы выбираем сами, основываясь на собственном опыте. 

А ведь преподавание курса «Теория вероятностей и статистика» требует от учителя кардинального изменения стиля своей работы: организации дискуссий, интенсивной устной работы, расширения собственного кругозора в областях других наук: биологии, географии, истории, литературы, и многое другое в дополнение к привычным методам и подходам к обучению. 

Аналогичные изменения должны произойти и в позиции ученика: должно измениться поведение учащегося на уроке и при подготовке к нему. Но дети привыкли к определенному стилю преподавания математики, требующему от них умения решать пусть и обширный, но заранее очерченный круг заданий. Зачастую они довольствуются тем, что умеют многократно воспроизводить изученный алгоритм и даже противятся попыткам решить задачу другим способом. Еще труднее решать с учениками обычного класса нестандартные задачи, тем более задачи повышенной сложности, в основе которых лежит редко используемый алгоритм решения задачи. 

Наблюдается ситуация, при которой ребенок не готов к собственной интеллектуальной активности и к аргументированному отстаиванию своей точки зрения. Значит, необходимо создание специальной среды, способствующей этим изменениям, и погружение в нее учащихся. Это — проведение практических работ, экспериментов, исследовательской и проектной деятельности непосредственно в ходе урока, активное участие в дискуссии, поиск информации за пределами школьного учебника, анализ массивов данных с целью выявления закономерности, самостоятельный выбор инструментария для своей работы, привлечение к работе на уроке и дома ИКТ. Эти требования усложняют жизнь и ученику, и учителю.

Изучение теории вероятности и статистики должно изменить и отношение учеников к случайному, которое часто идет вразрез с имеющимися у детей представлениями. Жизненный опыт учеников, фантазия порой только мешают, уводя в сторону от решения задачи. В опыте с монетой они видят не два исхода (орел, решка) или хотя бы три (добавим пресловутое ребро), но гораздо больше: подброшенную монету уносит птица, влетевшая в окно; монета попадает на люстру... Богатое воображение учащихся подлежит жесткому ограничению с самых первых уроков, когда мы определяем понятия «случайный эксперимент», «его исход», и говорим, что никакие фантастические условия не происходят во время его проведения. «Случайно» — это вовсе не «все что угодно». 

Представьте что-либо подобное на уроке алгебры, когда в задаче турист сначала шел пешком, потом ехал на машине... Ни разу эта избитая формулировка не была дополнена словами: «а вдруг машина поломается?». А вероятностные задачи... Кажется, им сама судьба предписывает расшатывать устоявшиеся школьные традиции, пробуждая в учащихся желание абсолютно непродуктивно досочинить своими догадками условие. 

«Вася не готов к тесту из 15 задач и отвечает наугад. Найдите вероятность того, что Вася даст хотя бы один верный ответ». Отвечают: «А может, ему повезет?». «Повезет, — говорю, — это другая отрасль, гаданием называется, а у нас — математическая наука, мы будем считать». На протяжении многих уроков надо формировать новое понимание: мы ищем закон, который управляет случайными процессами без влияния везения и фантастики. Как оказалось, стихийно это понимание не образуется.

Усвоение вероятностных и статистических понятий происходит только на уроках статистики и теории вероятностей, не подкрепляется при изучении прочих школьных предметов. На них по-прежнему царят неизбежность наступления ожидаемого результата, полная предсказуемость всех процессов. Вероятностное мышление со всем многообразием ожидаемых исходов не присутствует в их содержании. 

Знакомство с современными задачами экономики, с задачами целесообразности освоения новых районов, строительства промышленных объектов и железнодорожных магистралей, выбора мест строительства школ, больниц — остается за рамками школьного образования. Выпускник школы может и не догадываться, что за всем этим стоит современная математика.

Традиционная трудность математических дисциплин — анализ текста условия и, как следствие, умение решать сюжетные задачи — в данном предмете является решающей: все задачи — сюжетные! Для получения хорошей оценки за контрольную работу по алгебре можно безошибочно решить все задания на вычисления, преобразования выражений, решение уравнений и неравенств, то есть «технологичные» задания, и даже не приступать к текстовой задаче. Контрольная работа по теории вероятностей содержит только текстовые задачи. Безликих заданий, заданий «ни про что», вроде «вычисли», «реши уравнение», просто нет — «спрятаться» не за что. Несложные вероятностные задачи сводятся к одной или двум комбинаторным, решение которых ученики должны освоить за три урока. 

И надо иметь в виду, что сюжетные задачи по теории вероятности, комбинаторике и статистике гораздо разнообразнее, чем алгебраические. Помимо «классических» задач: бросание кубиков, монет, вытягивание наугад разноцветных карточек, существует огромное число прочих сюжетов. Решая «новую» задачу, понять, что это «старая», только что решенная задача, но в «новой упаковке», — дело очень трудное! Не очень подготовленные ученики не видят аналогию в задачах на вытаскивание из мешка разноцветных ручек или черных и белых пешек. 

Традиционные школьные разделы математики — это математика жестких связей и закономерностей, теория вероятностей — это математика в условиях неопределенных процессов, что важно для применения к прикладным вопросам современности. Если ощутить в полной мере мировоззренческую важность преподавания этого предмета, понять, что мир случайного будет открыт в школе именно учителем математики, то должны появиться силы для преодоления перечисленных выше трудностей. 

Трудно достижимые цели всегда больше радуют, приносят большее чувство удовлетворения. Успехи наших учеников, их заинтересованный взгляд отбрасывают прочь все колебания и внутреннее сомнение, являются демонстрацией нашего умения достичь поставленной цели. Чем больше «вложено» себя, своего времени, своего вдохновения, тем сильнее ощущение своей профессиональной компетентности, радости преодоления. 

 А что делать сегодня? Как же разобраться в преподавании нового предмета «Теория вероятностей и статистика», несущего нам всем: учителям, ученикам, их родителям, столько трудностей и тревог? Стоит ли менять свой привычный школьный образ жизни, привычные, годами обкатанные методы работы? Где найти время на погружение в содержательно новый раздел математики? На чьи методические советы и поддержку опереться в своей работе? 

Для себя я решила, что мне нужно полюбить этот предмет, как когда-то я полюбила геометрию. И по прошествии трех учебных четвертей по отношению к себе я могу сказать, что я сейчас на стадии глубокой симпатии почти ко всем содержательным разделам этого учебного курса. Я открыла для себя по-новому графы и круги Эйлера, понятие случайного события и задачи на бросание монеты и кубика.

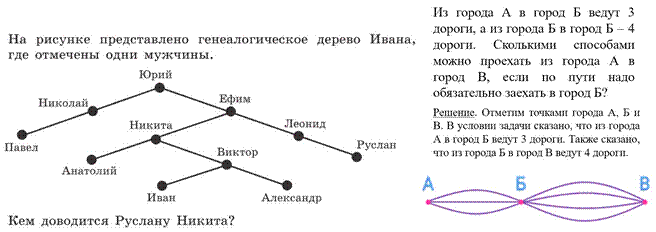
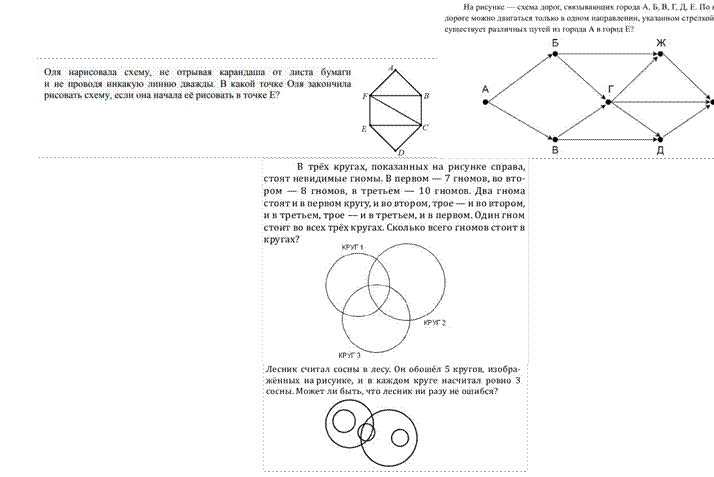
Рискну утверждать, что у любого заинтересованного учителя — при желании и большой работоспособности — все получится, ведь, по словам А.В. Луначарского, «учитель, который перестает учиться, перестает быть учителем». Значит, только в движении вперед мы состоятельны как учителя, и именно мы найдем, как сказал Норберт Винер, «скрытый порядок в хаосе, который нас окружает».