
МАОУК «Гимназия «Арт-Этюд»
Реализация принципа преемственности в условиях ФГОС
Аттестационная работа
Составитель:
Пермякова Светлана Николаевна
Должность:
Учитель математики
высшая категория
Екатеринбург, 2017
Введение |
3 |
Глава I Теоретические основания принципа преемственности в обучении учащихся школы в классах с углублённым изучением математики |
8 |
1.1. Особенности адаптационного периода. |
8 |
1.1.1. Понятие адаптации. |
8 |
|
1.1.2. Особенности подросткового возраста. |
9 |
|
1.2. Ключевые и метапреддметные компетенции |
13 |
|
1.3. Мониторинг учебных достижений |
16 |
Глава II Реализация принципа преемственности в обучении учащихся школы в классах с углублённым изучением математики |
17 |
|
2.1. Решение вопроса адаптации посредством развития ключевых и метапредметных компетенций |
17 |
|
2.2. Педагогические условия, направленные на эффективную реализацию принципа преемственности
|
20 |
|
2.3. Мониторинг учебных достижений учащихся |
23 |
2.4. Планирование дальнейшей работы на период до 2013 года |
26 |
Приложения |
28 |
Список литературы |
53 |
|
|
Введение
В «Концепции модернизации российского образования на период до 2020 года» [16] подчеркнуто, что уже в ближайшие годы роль образования в обществе и его ценность для современного человека должна поменяться коренным образом. В частности, изменения должна быть связаны с переходом от утилитарно-прагматических целей образования, ориентирующих его в основном на формирование знаний, умений и навыков к гуманистической направленности и развитию личности обучающегося, ее познавательных и индивидуальных способностей. Его результаты должны быть ориентированы на умение учащихся решать личностно-значимые и практически важные для них задачи.
Кроме того, главный смысл совершенствования структуры и обновления содержания обучения в школах состоит в том, что образование должно стать индивидуализированным, направленным на удовлетворение познавательных потребностей и интересов каждого обучающегося.
Отмеченные выше направления модернизации образования в современных условиях актуализируют на сегодня вопрос повышения эффективности обучения детей в школах с углубленным изучением предметов и созданием благоприятных условий для развития их способностей детей в различных видах деятельности.
В педагогической теории и практике учебных заведений уже накоплен определенный опыт решения разноаспектных вопросов обучения детей в школах и классах с углубленным изучением различных предметов(Ю.И Дик, Г.В. Дорофеев, А.А. Каверина, Н.Г. Миндюк, В.М. Монахов, А.А. Никитин, В.А. Орлов, А.А. Пинский, И.Э. Унт, В.В. Фирсов и др.). В концепции дифференциации обучения в школе исследованы различия профильного и углубленного обучения, определены роль и место таких школ и классов с углубленным изучением предметов. Учеными изучены условия организации уровневой дифференциации как обучения на различных уровнях глубины и сложности, разделения учебного коллектива на группы на основе разных показателей.
Вместе с тем, на сегодня недостаточно разработанными в науке и практике остаются вопросы, связанные с реализацией принципа преемственности в обучении учащихся в школах с углубленным изучением предметов, обеспечивающей эффективное развитие способностей детей в разных видах деятельности на всех ступенях непрерывного образования.
Проблема преемственности в обучении исследуется педагогикой уже не одно десятилетие и как многостороннее явление изучалось с разных сторон и исследовалось учеными в разных аспектах. Она рассматривается в науке как педагогическая система (А.В. Батаршев и др.), формы связи между элементами системы обучения (А.А. Люблинская и др.), педагогическое условие структурирования образовательного процесса (Э.С. Черкасова и др.), как принцип обучения (Ю.К. Бабанский, С.Я. Батышев, С.М. Годник, И.Т. Огородников, Г.И. Щукина и др.), как общепедагогическая закономерность (И.И. Прокопьев, А.Г. Мороз и др.). Осуществлению преемственности в содержании, формах и методах обучения посвящены работы М.Ф. Воробьёва, К.Р. Исаевой, С.С. Постовалова и др. Пути реализации принципа преемственности в начальной школе изучались В.И. Вдовиченко, А.М. Кухта, А.А. Люблинская. Дидактические основы преемственности в обучении между учебными предметами начальной и средней школы разрабатывались коллективом исследователей под руководством Ш.И. Ганелина, в трудах Л.В. Занкова, Е.С. Никифоровой, Н.С. Рождественского и др.
Вместе с тем, на сегодня остаются недостаточно исследованы особенности, педагогические условия и программно-методическое обеспечение реализации принципа преемственности в обучении учащихся в школах с углубленным изучением математики. На сегодня необходим поиск новых путей и средств рассматриваемого процесса при переходе детей с одной ступени общего образования на другую как базовой основы развития их математических способностей в таких учебных заведениях.
Итак, на сегодня явно обозначились следующие объективно существующие противоречия между:
1) возрастающими требованиями общества к развитию потенциальных способностей и возможностей детей и существующими традиционными подходами к реализации принципа преемственности в обучении учащихся на разных ступенях общего образования в школах, не всегда обеспечивающими должный уровень данного процесса;
2) стремлением школ (классов) с углубленным изучением математики обеспечить реализацию принципа преемственности в обучении учащихся начального – среднего – старшего звеньев и недостаточной разработанностью в педагогической теории обоснованных моделей данного процесса, условий и методики их эффективного развития.
Сформулированные противоречия обусловили актуальность проблемы, связанной с разработкой модели, направленной на эффективную реализацию принципа преемственности в обучении учащихся на всех ступенях школы в классах с углубленным изучением математики.
Важность рассматриваемой проблемы, ее недостаточная теоретическая и практическая разработанность послужили основанием для определения темы исследования: «Реализация принципа преемственности в обучении учащихся школы в классах с углубленным изучением математики».
Объект исследования: преемственность в обучении учащихся общеобразовательных школ.
Предмет исследования: реализация принципа преемственности в обучении учащихся в школах с углубленным изучением математики при переходе их с одной ступени общего образования на другую.
Цель исследования: разработать и проверить на практике модель реализации принципа преемственности в обучении учащихся начальной – средней – старшей школы в классах с углубленным изучением математики.
Гипотеза исследования: эффективная реализация принципа преемственности в обучении учащихся начальной – средней – старшей школы в классах с углубленным изучением математики возможна, если:
1) разработана и внедрена в практику учебного заведения модель данного процесса, основанная на системном, личностно-ориентированном и компетентностном подходах;
2) в рамках модели на примере математических дисциплин реализуется следующий комплекс педагогических условий:
- поэтапное введение в образовательный процесс «карты знаний» и оценочных листов группового и индивидуального развития для формирования положительной мотивации школьников в построении своей учебной траектории;
- последовательное использование личностно-развивающих заданий и задач, направленных на развитие специальных предметных и метапредметных компетенций учащихся в учебной и во внеучебной деятельности;
- оказание разносторонней поддержки обучающимся для их гибкой адаптации в переходный период.
В соответствии с поставленной целью и сформулированной гипотезой в работе решались следующие задачи:
1. Проанализировать состояние проблемы в педагогической науке и практике школ, уточнив признаки реализации принципа преемственности в обучении учащихся на разных ступенях школы в классах с углубленным изучением математики.
2. Разработать и обосновать модель реализации принципа преемственности в обучении учащихся начальной – средней – старшей ступеней школы в классах с углубленным изучением математики.
3. В рамках разработанной модели экспериментально проверить эффективность введения комплекса педагогических условий и личностно развивающей методики в рамках компетентностного подхода в образовании.
Теоретико-методологическую основу исследования составляют основные положения системного (С.И. Архангельский, В.П. Беспалько, Н.В. Кузьмина, Г.П. Щедровицкий и др.), личностно-ориентированного (Н.А. Алексеев, В.В. Давыдов, В.В. Сериков, И.С. Якиманская и др.) (И.А. Зимняя, Н.А.Селезнева, А.В.Хуторской) компетентностного подходов; положения теорий о развитии личности (Б.Г. Ананьев, Л.И. Божович, Л.С. Выготский, А.Н. Леонтьев, А. Маслоу, С.Л. Рубинштейн и др.).
Особое значение для нашего исследования имели учения о преемственности в образовании (Ю.К. Бабанский, Э.А. Баллера, А.В. Батаршев, А.Б. Воронцов, М.А. Вязовская, Ш.И. Ганелин, С.М. Годник, А.Г. Мороз, Л.К. Филатова и др.); психологические теории о развитии личности и реализации принципа преемственности на основе поэтапного формирования умственных действий (Б.Г. Ананьев, П.Я. Гальперин, Л.В.Занков, В.В. Давыдов, А.Н. Леонтьев и др.); теории индивидуализации обучения и исследования по профильной и уровневой дифференциации в образовании (О.С. Гребенюк, Ю.И. Дик, Г.В. Дорофеев, А.А. Каверина, А.А. Кирсанов, В.С. Мерлин, И.Э. Унт и др.); работы по педагогическому моделированию (С.И. Архангельского, В.П. Беспалько и др.).
Научная новизна исследования заключается в следующем:
1) теоретически обоснован и экспериментально проверен комплекс педагогических условий, направленный на реализацию принципа преемственности в обучении учащихся начальной – средней - старшей ступеней школы в классах с углубленным изучением математики;
2) обоснована и экспериментально проверена личностно развивающая методика реализации принципа преемственности в обучении учащихся начальной – средней - старшей ступеней школы в классах с углубленным изучением математики, направленная на развитие специальных предметных и метапредметных компетенций, самостоятельности школьников, формирование положительной мотивации в выстраивании учебной траектории, раскрытие потенциала и математических способностей в единстве применяемых форм, методов и средств обучения.
Теоретическая значимость исследования состоит том, что обоснованы требования системного и личностно ориентированного подходов в реализации принципа преемственности в обучении учащихся начальной – средней - старшей ступеней школы в классах с углубленным изучением математики, определены признаки реализации принципа преемственности, обоснованы типы и виды личностно-развивающих задач и заданий, необходимых для развития самостоятельности детей в учебной и внеучебной деятельности, разработаны формы и содержание «карт знаний» и оценочных листов группового и индивидуального развития.
В первой главе «Теоретические основания принципа преемственности в обучении учащихся школы в классах с углублённым изучением математики» определяется разработанность заявленной проблемы в теории и практике общеобразовательных школ; выявляется и уточняется терминологический аппарат исследования; подробно разбирается понятие адаптации; делается акцент на пути усовершенствования образовательной среды посредством развития ключевых и метапредметных компетенций.
Во второй главе «Работа по реализации принципа преемственности в обучении учащихся школы в классах с углублённым изучением математики» представлены возможные варианты совершенствования периода адаптации посредством развития специальных предметных и метапредметных компетенций, анализируются результаты работы.
В заключении изложены основные результаты и выводы исследования, намечены перспективы дальнейшего изучения проблемы.
Глава I
Теоретические основания принципа преемственности в обучении учащихся школы в классах с углублённым изучением математики
Несмотря на то, что проблема преемственности в обучении исследуется педагогикой уже не одно десятилетие, само понятие неоднозначно. В самом общем смысле оно понимается как объективная необходимая связь между старым и новым в процессе развития, подразумевающая не только ликвидацию старого, но и сохранение и дальнейшее развитие того прогрессивного, рационального, что было достигнуто на предыдущих ступенях, без чего невозможно движение вперед ни в бытии, ни в познании.
В зависимости от разных подходов к анализу данной категории, преемственность в педагогике определяется как педагогическое условие образовательного процесса (Э.С. Черкасова и др.), как принцип обучения (Ю.К. Бабанский, С.Я. Батышев, С.М. Годник, И.Т. Огородников, Г.И. Щукина и др.), как общепедагогическая закономерность и общепедагогический принцип (И.И. Прокопьев, А.Г. Мороз др.).
На современном этапе развития общества и модернизации образования проблема реализации принципа преемственности в обучении учащихся - весьма актуальна, поэтому исследованию ее различных аспектов посвящен целый ряд научных работ.
Для нашего исследования особенно актуальным является взгляд на преемственность в обучении школьников при переходе с одной ступени школьного образования на другую как общепедагогический принцип.
1.1. Особенности адаптационного периода.
1.1.1. Понятие адаптации.Термин «адаптация» трактуется как приспособление системы к реальным внешним условиям. Понятие адаптации (от латинского слова adapto-приспособляю) возникло в биологии и рассматривается в ней как приспособление строений и функций организма, его органов и клеток к условиям среды. Процессы адаптации направлены на сохранение гомеостаза, т.е. стабильности, равновесного психического состояния организма с окружающей средой. Адаптационные реакции на неблагоприятные воздействия имеют ряд общих черт и, следовательно, могут быть рассмотрены как целостный адаптационный синдром. В своем развитии процесс адаптации имеет несколько фаз, а именно: первоначальной декомпенсации, частичной и полной компенсации. По мнению психологов, социальная адаптация представляет собой процесс приспособления индивида к условиям социальной среды, и является одним из основных социально-психологических механизмов социализации личности, который, в свою очередь, включает в себя принятие индивидом социальной роли. [21: с. 16]
Социальная адаптация включает:
1. адекватное восприятие окружающей действительности и самого себя;
2. успешное общение и адекватные отношения с окружающими;
3. способность к труду, обучению и организации досуга и отдыха;
4. способность к самообслуживанию и самоорганизации;
5. изменчивость поведения в соответствии с ролевыми ожиданиями.
Социальная адаптация, таким образом, является объективно необходимым процессом вхождения индивида (группы) в новую социальную среду и освоения среды. Определяющую роль играет здесь такое взаимодействие и взаимное приспособление индивида и среды, в результате которого создаются условия с одной стороны для осуществления личностью ее потребностей и жизненных целей, с другой - для прогрессивного изменения самой адаптирующей среды. Таким образом, не только приспособление среды (системы) к интересам людей создает условия для более глубокой адаптации и самореализации личности, но и адаптированность личности, в свою очередь, способствует интеграции среды (системы), её стабильному развитию. В противном случае можно говорить о дезадаптации, (в частности, односторонней, а значит, неполной адаптации).
Значение социальной адаптации возрастает в условиях кардинальной смены деятельности и социального окружения человека. У учащихся и первых, и пятых, и десятых классов меняется их социальное окружение (новый состав класса и/или учителей) и система деятельности (содержание новой ступени образования). Переход учеников из начальной школы в среднюю — это сложный и ответственный период; от того, как пройдет процесс адаптации, зависит вся дальнейшая школьная жизнь ребенка. В этот период особо остро ощущается проблема снижения уровня учебных достижений. От снижения уровня успешности освоения программы напрямую зависит состояние здоровья учащихся и уровень мотивации учения, которые, в свою очередь, так же влияют на уровень успешности. Несомненно, существует ряд причин, влияющих на степень остроты данной проблемы. Оговоримся сразу, что брать во внимание фоновые факторы, те, на которые мы влиять не можем, не будем: это и резкое увеличение учебной нагрузки на учащихся, и изменение социального статуса ученика (в нашем понимании как младшего учащегося средней ступени обучения), и кадровая проблема.
1.1.2. Особенности подросткового возраста.
Первый адаптационный этап в школьной жизни подростка совпадает с возрастным периодом 10-11 лет, переходом от младшего школьного возраста к отрочеству. Как и любой переходный период, он имеет свои особенности и связан с определенными трудностями как для учащихся и их родителей, так и для учителей.В этот период происходят существенные изменения в психике ребенка. У него начинает развиваться теоретическое мышление, так как новые знания, новые представления об окружающем мире изменяют сложившиеся ранее житейские понятия. На основе развития нового уровня мышления происходит перестройка всех остальных психических процессов. Именно в этот период, по словам Д.Б.Эльконина, "память становится мыслящей, а восприятие думающим". Многочисленные исследования показывают, что развитие мышления в понятиях способствует дальнейшему развитию у детей рефлексии - понимания ими своей психической жизни, формирования отношения к самому себе. В результате у ребенка начинают развиваться собственные взгляды, мнение, в том числе понимание значимости образования. Познавательная сфера по-прежнему развивается как ведущая. Наиболее серьезные требования предъявляются к умственному и речевому развитию учащихся: навыки логических операций с понятиями, систематизация учебных знаний, перенос интеллектуальных навыков, понимание смысла изучаемых понятий, грамотность и содержательность устной речи. [24: c.213]
К концу младшего школьного возраста у учащихся должны быть сформированы и другие новообразования: произвольность психических процессов, способность к саморегуляции. Учебная деятельность дополняется другими видами деятельности, и все вместе теперь они влияют на психическое развитие учащихся, учебная деятельность при этом остается основной и продолжает определять содержание мотивационных сфер личности. С начала обучения в средней школе расширяется само понятие "учение", так как теперь оно может выходить за пределы класса, школы, может отчасти осуществляться самостоятельно, целенаправленно. Качественно изменяются требования к мотивации учебной деятельности. Появляется новый вид учебного мотива – мотив самообразования, представленный пока в наиболее простых формах (интерес к дополнительным источникам знаний). Кроме того, успешное обучение в среднем звене требует более глубоких и содержательных побудительных сил: ориентация на способы получения знаний, интерес к закономерностям и принципам, понимание смысла учения "для себя". Если интерес к учению становится смыслообразующим мотивом у ребенка, его учебная деятельность обеспечивает его успешное психическое развитие. К сожалению, социальная ситуация в современной школе такова, что в складывающейся иерархии ценностей учение не всегда занимает достойное место, познавательная активность школьников развита слабо, и только отметка выступает как главный стимул и основной конечный результат учебы. Рубеж 4-5-х классов, по свидетельству многих психологов и педагогов характеризуется некоторым снижением интереса к учебе в школе и самому процессу обучения. Это выражается в недовольстве школой в целом и обязательным ее посещением, нежелании выполнять дома учебные задания, в нарушении правил поведения в школе. Такие негативные проявления свойственны многим ученикам, но у тех из них, чье развитие уже было проблемным, имеется вероятность сохранения и закрепления негативных тенденций в устойчивых формах поведения. Таким образом, переход от детства к отрочеству характеризуется своеобразным мотивационным кризисом, вызванным сменой социальной ситуации развития и изменением содержания внутренней позиции школьника. К 4-5-му классу общение со сверстниками начинает определять многие стороны личностного развития ребенка. В этом возрасте проявляются притязания детей на определенное положение в системе деловых и личностных взаимоотношений в классе, формируется достаточно устойчивый статус ученика. Именно характер складывающихся взаимоотношений с товарищами, а не только его успехи в учебе и отношения с учителями, во многом определяет эмоциональное самочувствие ребенка. Существенно меняется также характер самооценки школьников этого возраста. Привычные в младших классах ситуации, когда самооценка определялась учителем на основании результатов учебы, подвергаются корректировке и переоценке другими детьми; при этом во внимание принимаются те качества ребенка, которые проявляются в общении.
Следующий адаптационный период соответствует 15-16 годам. Напомним основные особенности старших школьников:
1. Повышенная по сравнению с другими возрастами значимость тесных эмоциональных контактов.
2. Интенсивная социализация, сменяющая характерное для подростков противопоставление себя взрослому обществу. Это, в свою очередь, приводит к усилению негативных реакций и эмансипированного поведения со стороны старшеклассников, и к попыткам усилить контроль со стороны их родителей. В результате и дети, и родители переживают целый комплекс личностных проблем, который, повышает их тревожность.
Старшеклассник вынужден в короткий промежуток времени находить решения основных задач дальнейшего развития. Главная проблема заключается в том, что эти задачи, при множестве различных социальных институтов, способных оказывать ему в этом помощь, человек в период взросления должен решать самостоятельно. Тогда как "движение" личности старшеклассника в процессе решения этих задач всегда противоречиво, конфликтно, напряженно. Старший подростковый возраст является особенно чувствительным к формированию ценностных ориентаций, поскольку способствует становлению мировоззрения и собственного отношения к окружающей действительности.
Основным новообразованием в старшем подростковом возрасте традиционно считается жизненное и профессиональное самоопределение, осознание своего места в будущем. Оптимальным для благополучного развития личности является удовлетворенность настоящим и, в то же время, устремленность в будущее.
Развитие личности в условиях природного и предметного мира происходит через межличностные отношения; в частности, для подростков наиболее значимой становится сфера общения со сверстниками. Для них становится важным:
Главное новообразование юношеского возраста - открытие "Я", развитие рефлексии (отражение себя в своем образе "Я"), осознание собственной индивидуальности и ее свойств, появление жизненного плана, установки на сознательные сферы жизни, что направляет "Я" на практическое включение в различные виды жизнедеятельности. Этот процесс сопровождается различными проявлениями, как негативными, так и позитивными. Для подросткового периода свойственны беспокойство, тревога, раздражительность, диспропорция в физическом и психическом развитии, агрессивность, метания, противоречивость чувств, абстрактность бунта, меланхолия, снижение работоспособности. Позитивные проявления выражаются в том, что у подростка появляются новые ценности, потребности, ощущение близости с другими людьми, с природой, новое понимание искусства. Важнейшими процессами переходного возраста являются: расширение жизненного мира личности, круга ее общения, групповой принадлежности и увеличения числа людей, на которых она ориентируется. Для старшего подросткового возраста типичными являются внутренняя противоречивость, неопределенность уровня притязаний, повышенная застенчивость и одновременно агрессивность, склонность принимать крайние позиции и точки зрения. Чем резче различия между миром детства и миром взрослости, чем важнее разделяющие их границы, тем ярче проявляются напряженность и конфликтность
Общение подростков является своеобразной формой воспроизведения взаимоотношений, существующих в обществе взрослых людей, ориентации в нормах этих отношений и их освоения. Ведущий для подростковой стадии тип деятельности предполагает, что в данной деятельности взаимоотношения самих детей и взрослых должны быть весьма разнообразными и развернутыми (и следовательно, поддающимися регуляции и контролю) и иметь за собой вполне осязаемую значимую объективную цель.
1.2. Ключевые и метапреддметные компетенции
В мировой образовательной практике понятие компетентности выступает в качестве центрального, своего рода «узлового» понятия – ибо компетентность, во-первых, объединяет в себе интеллектуальную и навыковую составляющую образования; во-вторых, в понятии компетентности заложена идеология интерпретации содержания образования, формируемого «от результата» («стандарт на выходе со ступени, из школы»); в-третьих, ключевая компетентность обладает интегративной природой, ибо она вбирает в себя ряд однородных или близкородственных умений и знаний, относящихся к широким сферам культуры и деятельности (информационной, правовой и прочим).
Целый ряд именитых педагогов и психологов занимаются исследованиями в области компетентностного подхода к образованию (Н.А. Селезнева, И.А. Зимняя, В.А. Болотов, В.В. Сериков, Ю.Г. Татур, Л.Н. Боголюбов, В.С. Леднев, Н.Д. Никандров, М.В. Рыжаков, Н.А. Гришанова, С.Е. Шишов, В.А. Кальней, А.В. Хуторской, Д.Б. Эльконин и др.).
Причем, если термин «компетенция» обычно связывается с качествами личности, задаваемыми по отношению к определенному кругу процессов, нормативных обязанностей, полномочий и решаемых задач, то термин «компетентность» является практической реализацией компетенции, её воплощением в конкретных действиях и поступках в профессиональной деятельности, включая личностное отношение к этой деятельности. Компетентность - это латинское слово ("соответствую, подхожу") – означает знания и опыт в той или иной области. [Словари: 1: с. 614] Компетентность – это способность (умение) действовать на основе полученных знаний. В отличие от ЗУНов (предполагающих действие по аналогии с образцом) компетентность предполагает опыт самостоятельной деятельности на основе универсальных знаний.
Проблема отбора базовых (ключевых) компетенций является одной из центральных для обновления содержания образования.Один из характерных признаков ключевых компетенций – это многофункциональность. Поэтому овладение ими позволяет решать различные проблемы в повседневной, профессиональной или социальной жизни. Ключевые компетентности надпредметны и междисциплинарны, они применимы в различных ситуациях, не только в школе, но и на работе, в семье, в политической сфере и др.Ключевые компетентности требуют значительного интеллектуального развития: абстрактного мышления, саморефлексии, определения своей собственной позиции, самооценки, критического мышления и др.По словам «они многомерны, то есть включают различные умственные процессы и интеллектуальные умения (аналитические, критические, коммуникативные и др.), «ноу-хау», а также здравый смысл». [10: с. 25]Существенно, что все компетентности требуют различных типов действия: 1. действовать автономно и рефлексивно;
2. использовать различные средства интерактивно;
3. входить в социально-гетерогенные группы и функционировать в них.
По мнению современных педагогов и психологов в структуре ключевых компетентностей, должны быть представлены:- компетентность в сфере самостоятельной познавательной деятельности, основанная на усвоении способов приобретения знаний из различных источников информации, в том числе внешкольных;- компетентность в сфере гражданско-общественной деятельности (выполнение ролей гражданина, избирателя, потребителя);- компетентность в сфере социально-трудовой деятельности (в том числе умение анализировать ситуацию на рынке труда, оценивать собственные профессиональные возможности, ориентироваться в нормах и этике трудовых взаимоотношений, навыки самоорганизации);- компетентность в бытовой сфере (включая аспекты собственного здоровья, семейного бытия и прочее);- компетентность в сфере культурно - досуговой деятельности, (включая выбор путей и способов использования свободного времени, культурно и духовно обогащающих личность). [1:]Из приведенных определений становятся очевидными следующие особенности, отличающие компетентность от традиционных понятий – знания, умения, навыки, опыт:1. ее интегративный характер;
2. соотнесенность с ценностно-смысловыми характеристиками личности;
3. практико-ориентированная направленность.
Таким образом, компетенция - общая готовность установить связь между знанием и ситуацией, сформировать процедуру решения проблемы. Мы согласны с мнением Зимней И.А., предлагающей деление ключевых компетенций на три основные группы:1 группа: компетенции, относящиеся к самому себе как личности, как субъекту жизнедеятельности;
2 группа: компетенции, относящиеся к взаимодействию человека с другими людьми;
3 группа: компетенции, относящиеся к деятельности человека.[11: с. 3].
Отмечая еще раз, что компетенции это некоторые внутренние, потенциальные, сокрытые психологические новообразования (знания, представления, программы (алгоритмы) действий, системы ценностей и отношений), которые затем выявляются в компетентностях человека как актуальных, деятельностных проявлениях, обозначим, очертим сначала круг этих основных компетенций, имея в виду их дальнейшие проявления как компетентностей. Всего выделяем десять основных компетенций.
Компетенции, относящиеся к самому человеку как личности, субъекту деятельности, общения. Они суть:
§ компетенции здоровьесбережения: знание и соблюдение норм здорового образа жизни, знание опасности курения, алкоголизма, наркомании, СПИДа; знание и соблюдение правил личной гигиены, обихода; физическая культура человека, свобода и ответственность выбора образа жизни;
§ компетенции ценностно-смысловой ориентации в Мире: ценности бытия, жизни; ценности культуры (живопись, литература, искусство, музыка) науки; производства; истории цивилизаций, собственной страны; религии;
§ компетенции интеграции: структурирование знаний, ситуативно-адекватной актуализация знаний, расширение, приращение накопленных знаний;
§ компетенции гражданственности: знания и соблюдение прав и обязанностей гражданина; свобода и ответственность, уверенность в себе, собственное достоинство, гражданский долг; знание и гордость за символы государства (герб, флаг, гимн);
§ компетенции самосовершенствования, саморегулирования, саморазвития, личностной и предметной рефлексии: смысл жизни; профессиональное развитие; языковое и речевое развитие; овладение культурой родного языка, владение иностранным языком.
Компетенции, относящиеся к социальному взаимодействию человека и социальной сферы
§ компетенции социального взаимодействия: с обществом, общностью, коллективом, семьей, друзьями, партнерами, конфликты и их погашение, сотрудничество, толерантность, уважение и принятие другого (раса, национальность, религия, статус, роль, пол), социальная мобильность;
§ компетенции в общении: устном, письменном, диалог, монолог, порождение и восприятие текста; знание и соблюдение традиций, ритуала, этикета; кросскультурное общение; деловая переписка; делопроизводство, бизнес-язык; иноязычное общение, коммуникативные задачи, уровни воздействия на реципиента.
Компетенции, относящиеся к деятельности человека
§ компетенция познавательной деятельности: постановка и решение познавательных задач; нестандартные решения, проблемные ситуации — их создание и разрешение; продуктивное и репродуктивное познание, исследование, интеллектуальная деятельность;
§ компетенции деятельности: игра, учение, труд; средства и способы деятельности: планирование, проектирование, моделирование, прогнозирование, исследовательская деятельность, ориентация в разных видах деятельности;
§ компетенции информационных технологий: прием, переработка, выдача информации; преобразование информации (чтение, конспектирование), мультимедийные технологии, компьютерная грамотность; владение электронной интернет-технологией.
Эти компетенции, проявляясь в поведении, деятельности человека, становятся, как отмечалось нами выше, его личностными качествами, свойствами. Соответственно, они становятся компетентностями, которые характеризуются и мотивационными, и смысловыми, и отношенческими, и регуляторными составляющими, наряду с когнитивными (знанием) и опытом.
1.3. Мониторинг учебных достижений учащихсяДля того чтобы определить, как именно прошёл процесс адаптации учащихся к образовательной среде новой ступени школьного обучения, необходимо систематически отслеживать изменения в системе индивид – среда, определять динамику развития этой системы, то есть проводить мониторинг учебных достижений учащихся и процесса обучения в целом.Для решения задачи мониторинга мы используем квалиметрический подход. В чём он состоит? Квалиметрия — это область научного знания, изучающая методологию и проблематику разработки комплексных, а в некоторых случаях и системных количественных оценок качества любых объектов (предметов, явлений, процессов). [35: с. 49 – 54] «Качество» и «количество» отражают объективные стороны и отношения предметов, но содержание их разное. Разумеется, любое качество выражается в специфической для него совокупности количественных характеристик – спецификация работы. Качество и количество выступают как нечто раздельное лишь в абстракции. Реально они существуют в нерасторжимом единстве, образующем зону, «в пределах которой данное качество модифицируется, варьируется в силу изменения количества и отдельных несущественных свойств, сохраняя при этом свои существенные характеристики». [25: с. 237]Анализируя категории «качество» и «количество», мы вынуждены касаться фундаментальных понятий теории измерения (число, величина, оценка), которые трактуются по-разному. Мы придерживаемся следующего определения: величиной называется объект, полностью характеризующийся «заданием» одного числа, где число — форма отражения количества, оценка — суждения об определенном состоянии объекта, представленные в качественной или количественной форме. [29: с. 52]В связи с этим идёт поиск адекватных способов модернизации содержания образования, освоение и внедрение новых образовательных технологий, направленных на решение задач процесса обучения.
Интересующая нас социальная адаптация учащихся рассматривается с точки зрения учебной деятельности (УД). Поэтому мы считаем, что результативность адаптационного периода можно рассматривать через оценку уровня успешности учащихся в рамках УД. Именно эта категория будет для нас наиболее показательна для изменения условий образовательной среды.
Объектом мониторинга выступает учебный процесс. Предметом – учебные достижения как результаты учебного процесса.
Когда мы говорим об оценке достижений учащихся, мы чаще всего рассматриваем специальные знания и умения. Для решения противоречия субъективизма при оценивании учащихся вводится ГОС, цель которого обеспечить каждого ученика одинаковыми возможностями при получении образования. Мы будем применять мониторинг учебной деятельности в рамках ГОСа и образовательной программы по предмету в МОУ СОШ №178.
Глава II
Реализация принципа преемственности в обучении учащихся школы в классах с углублённым изучением математики
2.1. Решение вопроса адаптации посредством развития ключевых и метапредметных компетенций
Трудности, с которыми необходимо справиться ученику в период перехода с одной ступени школьного образования на другую, требуют высокого уровня развития компетенций. Компетенции первой группы будут определять адекватность ребёнка по отношению к тем физиологическим изменениям, которые происходят в возрасте 11 – 12, 15 – 16 лет. Входящие в эту группу компетенции гражданственности (знание и соблюдение прав и обязанностей гражданина, ответственность, уверенность в себе) позволят ученику успешно адаптироваться к новым условиям. Компетенции самосовершенствования, саморазвития и рефлексии будут определяющими при развитии и дальнейшем формировании Я-концепции ученика. [23: 109]Развитие второй группы компетенций (социальное взаимодействие с обществом, коллективом, семьей, друзьями, сотрудничество, принятие другого; компетенции коммуникативные) помогут ученику справиться с трудностями межличностного общения в новой окружающей среде. Младший подросток с его возрастными изменениями уже не получает устойчивого переживания успешности или не успешности в узких рамках отношений с одним учителем. Более того, педагог, пришедший из старшей школы в среднюю, часто механически переносит стиль взаимоотношений, сложившийся со старшеклассниками, на учащихся 5-го класса. Например, предъявление высоких требований относительно учебной деятельности, новых форм без этапа предварительного научения или объяснения причин. Изменяется и стиль общения родителей с детьми, которые всё меньше помогают своему ребёнку, ссылаясь на его "взрослость". Совершенно по-другому, не так как в начальной школе, строятся отношения со сверстниками. Подросток 15-16 лет сталкивается с проблемой жизненного и профессионального самоопределения, осознания своего места в будущем и, в то же время, часто ограничен рамками одного учебного заведения. Успех в расширении жизненного мира личности, круга ее общения, групповой принадлежности и увеличения числа людей, на которых она ориентируется, зависит от уровня развития компетенций социального взаимодействия и общения.В современных условиях в начальной школе действует наряду с традиционной технологией ряд развивающих, таких как «Школа – 2100», Виноградова, Занкова. Обучению на средней ступени школьного образования характерны традиционные методы и формы обучения. Старшая школа – профильная школа. Таким образом, при переходе с одной ступени школьного образования на другую естественным становится смена технологий, которая в свою очередь влияет на смену видов деятельности учащихся. Помогает справиться с этой трудностью третья группа компетенций. К ней относятся компетенции:· познавательной деятельности (постановка и решение познавательных задач, продуктивное и репродуктивное познание, исследование);
· деятельности (средства и способы деятельности: планирование, проектирование, прогнозирование);
· информационных технологий (приём, переработка, выдача информации).
Хорошо развитые компетентности этой группы позволяют учащимся справиться с перегруженностью учебных программ, предусматривающих высокий уровень развития различных форм мышления, высокий уровень развития речи, отвечающую требованиям средней школы способность к умозаключениям у большинства учащихся, хорошее развитие навыков самостоятельной работы, стремление работать на высоком уровне сложности и т.п. Таким образом, мы видим, что степень адаптивности школьника напрямую зависит от компетенций и компетентностей, которыми он обладает. Последние могут и должны выступать необходимым условием успешности ученика в период адаптации к новым школьным условиям.
Проведенный анализ различных подходов к определению компетенций (компетентностей) позволил, как отмечалось выше, сделать несколько выводов.
Во-первых, исследователи отмечают деятельностную, актуальную сущность компетентности, подчеркивая, что в отличие от знаниевой характеристики, т.е. характеристики «что», здесь акцентируется способ и характер действия «как».
Во-вторых, большинство исследователей отмечают личностную, в частности мотивационную характеристику компетентности.
В-третьих, исследователи фиксируют сложный характер этого явления в его определении и в оценке.
Для регулирования учебно-образовательного процесса по математике и внеучебной деятельности учащихся в рамках адаптивно-компетентностного подхода, на наш взгляд, необходимо использовать деятельностные позиции. Общие установки: 1. целевой ориентацией является развитие гражданского общества и становление граждан, способных самостоятельно и в группе решать проблемы стабильного развития этого общества, в широком смысле таких граждан можно назвать общественными деятелями;
2. общественный деятель или общественно активный гражданин действует в следующих пяти позициях: исследователь, участник и организатор коммуникации; организатор индивидуальных и коллективных действий, субъект принятия решений и учащийся.
Примерный список навыков и техник представлен в таблице 1 «Деятельностные позиции, развивающие компетентность личности».
Таблица 1 Деятельностные позиции, развивающие компетентность личности
Компетенции |
№ |
Позиции и умения |
Методологические приёмы |
Компетенции, относящиеся к самому человеку как личности, субъекту деятельности, общения. |
Учащийся |
||
1. |
Планировать решение учебных задач и процесс образования |
· Планирование учебного процесса. · Оценивание и самооценивание. · Выбор критериев оценивания. · Рефлексивные обсуждения процесса учения. · Выбор учебных средств. |
|
2. |
Оценивать собственное продвижение в знаниях и умениях |
||
3. |
Анализировать (рефлектировать) процесс учения, представлять его в тексте и схемах |
||
4. |
Организовывать собственный процесс учения |
||
Организатор и участник принятия решений |
|||
1. |
Анализировать конкретные случаи |
· Разбор проблемных ситуаций. · Прогнозирование последствий принимаемых и принятых решений. · Подготовка обобщений и выводов. · Определение причин возникновения проблем. · Оценка решения по заданным критериям. · Ролевые игры, посвященные принятию решений. |
|
2. |
Оценивать необходимость и достаточность данных для принятия решения |
||
3. |
Синтезировать данные |
||
4. |
Предсказывать возможные последствия совершенного действия |
||
5. |
Принимать решения |
||
|
Компетенции, относящиеся к социальному взаимодействию человека и социальной сферы |
Организатор социального действия |
||
1. |
Работа в группе на разных ролях |
Участие в ролевых играх.· групповая работа; · контроль выполнения планов; · разработка и реализация проектов. |
|
2. |
Организация групповой работы |
||
3. |
Уточнение цели и задачи работы |
||
4. |
Составление и реализация проектов |
||
5. |
Оценка ресурсов |
||
Организатор и участник коммуникации |
|||
1. |
Активно слушать |
Ролевые игры.Тематические дискуссии их организация и проведение: · процедуры активного слушания; · беседа с гостем; · публичные выступления; · анализ конфликтов; · драматизация; · дебаты. |
|
2. |
Понимать и интерпретировать различные точки зрения |
||
3. |
Дискуссионные навыки |
||
4. |
Умение убеждать в своей точке зрения |
||
5. |
Использовать различные жанры коммуникации |
||
6. |
Посредничество в конфликтах |
||
Компетенции, относящиеся к деятельности человека |
Социальный исследователь |
||
1. |
Ставить вопросы |
Сбор необходимых данных: · поиск данных в электронных носителях информации; · интерпретация данных; · проведение интервью и опросов; · наблюдение и анализ данных по заданным критериям; · критический обзор литературы. |
|
2. |
Формулировать гипотезы |
||
3. |
Сравнивать и различать информацию |
||
4. |
Работать с теоретической и справочной литературой |
||
5. |
Предлагать собственный план исследования и уточнять предмет исследования |
||
Мы считаем, что для того, чтобы помочь учащемуся преодолеть трудности и организовать процесс обучения, ориентированный на развитие компетентностей, преподаватели должны обладать информацией о мотивах и интересах обучающегося. Основываясь на данных наблюдениях, должны предлагать такие задачи, которые создают познавательную мотивацию и опираются на уже развитых у него компетенциях. Поэтому необходимо тесное сотрудничество учителя-предметника и классного руководителя с психолого-педагогической службой в образовательном учреждении.
2.2. Педагогические условия, направленные на эффективную реализацию принципа преемственности
На наш взгляд, комплекс педагогических условий, направленный на эффективную реализацию принципа преемственности в обучении учащихся начальной – средней – старшей ступеней школы в классах с углубленным изучением математики должен вбирать в себя следующие условия:
1) поэтапное введение в образовательный процесс «карты знаний» и оценочных листов группового и индивидуального развития для формирования специальных предметных и метапредметных компетенций школьников и построения своей учебной траектории;
2) последовательное использование личностно-развивающих заданий и задач, направленных на развитие познавательной самостоятельности учащихся в учебной и во внеучебной деятельности;
3) оказание разносторонней поддержки обучающимся для их гибкой адаптации в переходный период.
Данные условия взаимозависимы и дополняют друг друга. Необходимость введения нами первого условия связана с формированием в переходный период у школьников мотивации в построении своей учебной траектории, что влияет на приобретение значимого для них смысла учебной деятельности, желание осознанно координировать свои действия, отслеживая личные результаты в учебе.
Мы полагаем, что в школе с углубленным изучением математики формированию мотивации в построении школьниками учебной траектории, развитию их компетенций способствует использование в учебном процессе «карты знаний» и оценочных листов индивидуального и группового развития детей. При этом формируются и развиваются следующие ключевые предметные и метапредметные компетенции:
Компетенции, относящиеся к самому человеку как личности, субъекту деятельности, общения. Даная компетенция включает постановку ученика в ситуацию самоопределения. Если говорить относительно уроков математики, то мы должны в течение учебного процесса выявить математически способных учеников и помочь им в ситуации самоопределения. Собственно говоря, речь здесь идёт о профориентации. Конечно, кто-то может сказать, что рано проводить профориентацию на рубеже начальной и основной школы, но ведь именно в эти школьные годы мы способствуем выбору детьми той сферы, которая им наиболее интересна — это либо гуманитарная сфера, либо сфера точных наук.
На наш взгляд данные компетенции являются наиболее важными, они предполагают овладение учеником знаниями и опытом в гражданско-общественной деятельности, в социально-трудовой сфере, в области семейных отношений и обязанностей, в вопросах экономики и права, а так же в профессиональном самоопределении. Т.е. подразумевают овладение детьми теми предметными знаниями, умениями и навыками, которые они будут использовать непосредственно в своей дальнейшей жизнедеятельности. Именно в начальной школе на уроках математики дети научаются считать, вычислять, измерять и так далее и совершенствуют свои умения в среднем звене. Таким образом, необходимо постоянное закрепление, усовершенствование и контроль над данными базовыми умениями.
Компетенции, относящиеся к социальному взаимодействию человека и социальной сферы, подразумевают, что непосредственно на уроках математики мы должны знакомить учеников с общественной моралью и традициями. Т.е. учителю необходимо внедрять такие приёмы работы на уроке, которые не отвлекали бы урок от основного содержание, но при этом были бы с подтекстом, благодаря которому ученики несознательно усваивали бы общекультурные компетенции. Входящая в этот блок коммуникативная компетенция подразумевает под собой владение учеником средствами коммуникации. Необходимо, чтобы ученик на уроках общался с одноклассниками, умел истолковать для них материал. Т.е. создание коммуникационных приёмов на уроках математики подготавливает ученика к реализации себя в социуме.
Компетенции, относящиеся к деятельности человека, представляют собой совокупность учебных ситуаций, в которых ученик выступает как субъект и как объект процесса обучения одновременно, т.е. в данном случае речь идёт о самообучении. Соответственно реализация компетентностного подхода в части учебно-познавательной компетенции подразумевает использование учителем приёмов, способствующих обучению и развитию у учеников способности к самообразованию.
Компетенции информационных технологий в своей сути заключает процесс освоения учеником современных информационных технологий. Т.е. на уроке математики мы должны, как всегда, непреднамеренно для ученика, обучить его способам работы с информационными технологиями. От урока к уроку необходимо повышать уровень «первоисточников», таким образом, подготавливая ученика к адаптации в информационном пространстве современного мира.
Введение второго педагогического условия объясняется тем, что только последовательное введение личностно-развивающих заданий и задач обеспечивает развитие познавательной самостоятельности учащихся в учебной и внеучебной деятельности. Самостоятельность же играет важную роль для подготовки пятиклассников к дальнейшему обучению в классах с углубленным изучением предмета.
Таблица 2 Виды заданий и формы деятельности, направленные на развитие компетенций
|
Компетенции |
Виды заданий и задач |
Формы деятельности |
|
1 группа |
Задания на постановку цели и задач |
Международная игра-конкурс «Кенгуру»; Межвузовская академическая олимпиада; Олимпиада по основам наук по УрФО; Задачи со скрытой информативной частью; Задачи с «лишними данными». |
|
Задания на выявление проблемы |
||
|
Задания на составление алгоритма действий |
||
|
Задания на выявление различных способов решения проблемы |
||
|
Задания на выбор рационального способа решения |
||
|
Задания на нахождение ошибок и исправление их |
||
|
Задания на контроль и оценку своих действий |
||
|
2 группа |
Задание на определение проблемной ситуации |
Дискуссия, групповая работа, парная работа; Проведение проверочных работ в форме теста. |
|
Задания на контроль и оценку сотрудничества |
||
|
3 группа |
Задания на поиск необходимой информации |
Работа с Интернет. Работа в библиотеке. Работа на уроке с научными текстами. Обучение написания конспектов, тезисов, лекций. |
|
Задания на составление задач и вопросов к ним |
||
|
Задания по выбору научного проекта |
||
|
Задания по составлению научного проекта |
||
|
Задания по защите научного проекта |
Использование подобных заданий и задач позволяет школьникам уже с начальной школы, а затем в среднем звене научиться самостоятельно оценивать учебную ситуацию, формулировать проблему, самостоятельно выдвигать возможные альтернативные пути ее решения, осуществлять выбор рационального подхода к осуществлению задуманного, решать сложные нестандартные и олимпиадные задачи и контролировать при этом свои действия.
Особого внимания заслуживают, на наш взгляд нестандартные задачи, применяемые в работе, которые способствуют развитию их логического мышления, пространственного воображения, исследовательских навыков, смекалки детей, а также оживляют учебный процесс, повышая интерес учащихся к предмету математики. Задачи такого рода должны предлагаться учащимся легко и непринужденно, почти в импровизированном стиле. При этом каждый учащийся решает столько задач, сколько сможет, и выполняет те задания, которые ему представляются интересными.
Развитию познавательной самостоятельности учащихся способствуют задания, связанные с выбором, выполнением и защитой научного творческого проекта детей, способных к математике.
Таким образом, мы предложили свои варианты реализации ключевых образовательных компетенций на уроках математики в начальной и средней школе. Предложенные разработки могут быть модернизированы, изменены или дополнены.
2.3. Мониторинг учебных достижений учащихся
Уровни достижений учащихся мы можем рассматривать в двух направлениях: как уровень усвоения и как уровень увеличения объёма содержания.
В каждом из направлений мы выделяем следующие промежутки:
1. Уровень усвоения разобьём на:
а) Описательный или базовый (репродуктивный);
б) Алгоритмический (репродукция по образцу);
в) Аналитико-синтетический (репродуктивный с элементами продукции);
г) Творческий (продуктивный).
2. Уровень увеличения объёма - на:
а) Ориентировочный;
б) Базовый (минимальное содержание в ГОСе);
в) Программный;
г) Сверхпрограммный (факультативы, элективные курсы, исследовательские проекты).
Для нас наиболее интересны уровни усвоения учащимися учебного материала. Какие показатели качества знаний, умений и навыков определяются на каждом уровне, и, соответственно, какие виды заданий мы можем для этого использовать, показано в таблице №3.
Таблица 3 Показатели уровней усвоения учащимися учебного материала
|
Уровни достижений |
Показатели качества |
Типы заданий-определителей |
|
Описательный (репродуктивный) |
Прочность - воспроизведение на уровне признака, родовидовых понятий |
Воспроизведение освоенной информации об изучаемых объектах.
|
|
Алгоритмический (репродуктивный по образцу) |
Мобильность - способность применять знания в действиях по образцу |
Применение освоенных алгоритмов в знакомых ситуациях.
|
|
Аналитико-синтетический (репродуктивный с элементами продукции) |
Действенность - способность применения знания в незнакомых, нестандартных ситуациях |
Действие в незнакомой ситуации, поиск алгоритмов решения сложных задач.
|
|
Творческий (продуктивный) |
Гибкость мышления, критичность, системность, глубина, устойчивость - способность зафиксировать внимание на ключевых существенных признаках |
Готовность к самостоятельному принятию решений (самостоятельность в различных видах деятельности).
|
Результаты административных контрольных работ по математике представлены в Приложении 1.
Использование методологических приёмов и форм деятельности, направленных на формирование ключевых предметных и метапредметных компетенций, позволяет достигать высокого уровня учебных достижений учащихся по математике. Представленные в таблице данные лонгэтюдного исследования успешности учащихся посредством анализа контрольных работ, показывает стабильные коэффициенты средней степени обученности и качества обучения учащихся.
Таблица 4 Коэффициенты СОУ и качества обучения
|
Контрольные работы |
Всего |
Писали |
"5" |
"4" |
"3" |
"2" |
СОУ |
Качество |
|
5 класс ноябрь |
29 |
26 |
6 |
6 |
8 |
6 |
0,52 |
0,46 |
|
5 класс май |
28 |
27 |
9 |
12 |
5 |
1 |
0,69 |
0,78 |
|
6 класс |
27 |
21 |
11 |
5 |
2 |
3 |
0,73 |
0,76 |
|
7 класс |
29 |
25 |
10 |
8 |
5 |
2 |
0,69 |
0,72 |
|
8 класс |
29 |
26 |
10 |
10 |
6 |
0 |
0,71 |
0,77 |
Эффективность введения комплекса педагогических условий, направленных на реализацию принципа преемственности в обучении математике учащихся при переходе с первой ступени школьного образования на вторую, была проанализирована по следующим показателям:
1. уровень знаний и умений на уроках математики (квалиметрический подход);
2. мышление учащихся на уроках математики (психологические исследования, квалиметрический подход);
3. спокойствие учащихся на уроках математики (психодиагностика школьной тревожности, Кондаш, 1973; Цветометодика);
4. внимание учащихся на уроках математики (психологические исследования).
Результаты данного исследования приведены в таблице 5.
Таблица 5 Прирост по категориям среди классов параллели
|
Прирост (G) по отдельным критериям |
Группы учащихся |
||
|
Класс Е |
Среднее по другим классам параллели |
||
|
(G) по уровню знаний и умений на уроках математики |
низкий уровень |
-22,22% |
-3,71% |
|
средний уровень |
-11,11% |
3,71% |
|
|
высокий уровень |
33,33% |
0,00% |
|
|
(G) по мышлению учащихся на уроках математики |
низкий уровень |
-29,63% |
-2,00% |
|
средний уровень |
3,70% |
0,00% |
|
|
высокий уровень |
25,93% |
5,00% |
|
|
(G) по спокойствию учащихся на уроках математики |
низкий уровень |
-22,22% |
7,41% |
|
средний уровень |
-11,11% |
-3,71% |
|
|
высокий уровень |
33,33% |
-3,70% |
|
|
(G) по вниманию учащихся на уроках математики |
низкий уровень |
-18,52% |
14,81% |
|
средний уровень |
-22,22% |
-11,11% |
|
|
высокий уровень |
40,74% |
-3,70% |
|
Полученные расчёты подтвердили наше предположение, что введение предложенного нами комплекса педагогических условий модели способствует эффективной реализации принципа преемственности при переходе учащихся из начальной в основную ступень школы с углубленным изучением математики. Таким образом, полученные результаты исследования дают основание сделать обобщенный вывод, что выдвинутая гипотеза нашла свое подтверждение, задачи научного поиска решены, цель исследования достигнута.
2.4. Основные выводы исследования и планирование дальнейшей работы на период до 2021 года
1. В ходе исследования было установлено, что проблема реализации принципа преемственности в обучении учащихся начальной и основной ступеней школы с углубленным изучением математики является актуальной в педагогической теории и практике и требует дальнейшего теоретического осмысления.
2. Основными признаками реализации принципа преемственности в обучении учащихся начальной – средней – старшей ступеней школы с углубленным изучением математики выступают: принятие общей для этих ступеней основной идеи, цели и содержания образования, методов, организационных форм обучения, методики оценки результативности обучения; наличие эмоциональной и психологической близости учителя и детей; обеспечение самореализации школьника, сохранение оптимального общего развития детей и раскрытие их математических способностей
3. Выявлено и доказано, что комплекс педагогических условий, направленный на эффективную реализацию принципа преемственности в обучении учащихся начальной – средней – старшей ступеней школы в классах с углубленным изучением математики, представлен в модели следующими условиями:
- поэтапное введение в образовательный процесс «карты знаний» и оценочных листов группового и индивидуального развития для формирования положительной мотивации школьников в построении своей учебной траектории;
- последовательное использование личностно-развивающих заданий и задач, направленных на развитие ключевых предметных и метапредметных компетенций;
- оказание разносторонней поддержки обучающимся для их гибкой адаптации в переходный период.
4. Апробирована личностно развивающая методика, направленная на эффективную реализацию принципа преемственности в обучении учащихся начальной – средней – старшей ступеней школьного образования в классах с углубленным изучением математики
5. Обосновано, что реализация принципа преемственности представляет собой уровневый процесс. Критериями для оценки уровня реализации принципа преемственности в обучении учащихся начальной – средней – старшей ступеней школы с углубленным изучением математики являются знания и умения, спокойствие, мышление и внимание учащихся на уроках математики.
7. Проведенный анализ полученных статистических расчетов экспериментальной работы показал, что выдвинутая гипотеза нашла свое подтверждение, задачи научного поиска решены, цель исследования достигнута.
Мы полагаем, что предложенное исследование не исчерпывает всех аспектов обозначенной проблемы. Дальнейшая работа может быть посвящена подтверждению правильности выбранных педагогических условий, направленных на реализацию принципа преемственности в обучении учащихся основной и старшей ступеней школы с углубленным изучением математики; реализации принципа преемственности школ с углубленным изучением предметов и вузов.
Таблица 6 Основные направления работы на 2016-2021 учебные годы
№ |
Задачи |
Предполагаемый результат |
Сроки |
1. |
Продолжить изучение научно-педагогической литературы |
Накопление теоретических знаний современной педагогической науки.Участие в педагогических чтениях и конференциях. |
2017-2020 |
2. |
Продолжение мониторинга уровня учебных достижений по математике |
Использование результатов мониторинга в педагогической деятельности |
2017-2020 |
3. |
Продолжить исследование влияния компетентностей на успешность учащихся по математике |
Проведённые исследования |
2017-2020 |
4. |
Расширить методологию компетентностей на практике |
Применить методологию компетентностей на практике |
2017-2020 |
5. |
Разработать методические рекомендации для учителей и учащихся по организации процесса преемственности |
Учебно-методическое пособие «Реализация принципа преемственности в школе с углубленным изучением математики». |
2020 |
6. |
Написание диссертации по теме «Вопросы адаптации в современных русских и зарубежных исследованиях» |
Защита диссертации |
2018 |
7. |
Написание аналитического отчёта |
Аналитический отчёт за межаттестационный период |
2021 |
Результаты мониторинга представлены в сборнике научных статей V международной научно-практической конференции «Управление качеством образования: проблемы непрерывного образования» в статье «Роль мониторинга качества образования в успешности адаптации школьников во время перехода на основную ступень обучения». Пленарные и секционные доклады состоялись 4-5 апреля 2006 года.
Вторая публикация представлена в сборнике 12 педагогических чтений 2006 работников системы образования г. Екатеринбурга «Компетентностный подход в образовании: достижения, проблемы и опыт образовательной практики Екатеринбурга» и называется «Ключевые компетенции и компетентность младшего школьника как условие успешности ученика в период адаптации при переходе на 2 ступень школьного образования».
Подана заявка на участие в городском Форуме учителей математики «Модернизация математического образования: актуальные вопросы методики преподавания в школе», который пройдёт в рамках работы городской ассоциации учителей математики с деканатом математического факультета УрГПУ, кафедрой ТиМОМ 25-26 марта 2016 года.
Приложение 1
![]() Анализ работ учащихся 5 «А» класса.
Анализ работ учащихся 5 «А» класса.
Учитель: Пермякова Светлана Николаевна
Контрольная работа по математике (преемственность) в 5 классе за 2015-2016 учебный год.
Цель работы:
Таблица № 1 СПЕЦИФИКАЦИЯ КОНТРОЛЬНОЙ РАБОТЫ
|
№ задания |
Содержание задания |
Определяемый уровень качества |
Максимальный балл |
|
1. |
1. Нахождение неизвестного компонента действий 2 ступени |
Базовый |
1 |
|
2. Правильность арифметических вычислений |
Ниже базового |
1 |
|
|
3. Нахождение неизвестного компонента действий 1 ступени |
Базовый |
1 |
|
|
4. Правильность арифметических вычислений |
Ниже базового |
1 |
|
|
2. |
1. Определение порядка выполняемых действий |
Алгоритмический |
1 |
|
2. Правильность выполнения арифметических действий 2 ступени с многозначными числами |
Базовый |
1 |
|
|
3. Правильность выполнения арифметических действий 1 ступени с многозначными числами |
Базовый |
1 |
|
|
3. |
1. Знание формулы для нахождения площади квадрата |
Алгоритмический |
1 |
|
2. Правильность вычислений |
Ниже базового |
1 |
|
|
4. |
1. Умение переводить из одной единицы измерения в другую |
Алгоритмический |
1 |
|
5. |
1. Умение определить правильный порядок действий в текстовой задаче |
Аналитико-синтетический |
1 |
|
2. Составление математической модели учебной задачи |
Аналитико-синтетический |
1 |
|
|
6. |
Применение знаний в незнакомой учебной ситуации |
Аналитико-синтетический |
1 |
|
|
Максимальный балл: |
13 |
|
Содержание работы.
Первый вариант.
![]()
![]()
8т368кг+5т279кг *** 13т547кг;
4ч25мин-45мин *** 3ч80мин.
Второй вариант.
![]()
![]()
9т273кг+4т689кг *** 13т852кг;
5ч35мин-55мин *** 4ч80мин.
1. В классе 30 человек.
2. Писали работу 28 учеников.
3. В работе представлено 6 заданий. В соответствии со спецификацией денной работы мы можем говорить о том, что в ней представлены задания не выше аналитико-синтетического уровней. Так как все задания являются заданиями с открытым ответом, то поправку на угадывание мы можем не делать.
4. Максимальное количество баллов, которое можно набрать, верно выполнив все 6 заданий, составляет 13 баллов. Переведём сырой балл в шкалу школьных отметок.
a. 12 – 13 баллов – «5»;
b. 10 – 11 баллов – «4»;
c. 6 – 9 баллов – «3»;
d. Меньше 6 баллов – «2».
5. Найдём средний уровень группы. Хср=10,14 баллов
6. Степень сложности работы.
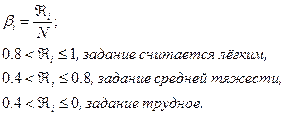
Так как средний уровень ранга трудности каждого задания составляет 0,72, то для данной группы учащихся контрольная работа оказалась средней трудности.
7. Вычислим размах. R = 13 – 4 = 9
Коэффициент вариации равен Кл = ![]()
Поэтому данный класс учащихся можно назвать как однородный класс.
8. Анализ результатов выполнения каждого задания.
В таблице № 1 рассмотрена спецификация работы. Учащийся набирает 1 балл за верно выполненный шаг, определённый для проверки, каждого задания.
Поэтому введём нумерацию вида 1.1., 1.2.,1.3.,1.4.,2.1.,2.2.,2.3.,3.1.,3.2.,4.,5.1.,5.2..6.
Ранг трудности каждого номера для данного класса представлен в таблице № 6.6.
На рисунке № 9 «Карта трудности Шухарта» мы видим, что учащиеся справились со всеми заданиями базового уровня.
9. К наиболее типичным ошибкам относится знание и применение формулы площади квадрата.
10. Выразим достижения каждого ученика в процентах.
11. В таблице № 8.6. мы видим процентное выражение п. 10 данного анализа.
12. Данные таблицы № 8.6. представлены в структурной диаграмм
Таблица № 6.6. Учебные достижения учащихся 5 «А» класса
|
№ п\п |
Ф. И. |
1. |
1. |
1. |
1. |
3. |
2. |
2. |
4. |
2. |
5. |
5. |
3. |
6. |
∑ |
|
1. |
3. |
4. |
2. |
2. |
1. |
3. |
2. |
1. |
2. |
1. |
|||||
|
1. |
Бровко |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
13 |
|
2. |
Галиева |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
13 |
|
3. |
Зяблова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
13 |
|
4. |
Санатина |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
13 |
|
5. |
Седнев |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
13 |
|
6. |
Белоусов |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
12 |
|
7. |
Бондаренко |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
12 |
|
8. |
Горбачёв |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
12 |
|
9. |
Карпова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
12 |
|
10. |
Салтыков |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
12 |
|
11. |
Бабурина |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
11 |
|
12. |
Жемальдинов |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
11 |
|
13. |
Федоренко |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
11 |
|
14. |
Минина |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
10 |
|
15. |
Муллоянов |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
10 |
|
16. |
Новикова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
10 |
|
17. |
Широкова |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
10 |
|
18. |
Банных |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
9 |
|
19. |
Никулин |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
9 |
|
20. |
Привалихина |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
9 |
|
21. |
Снеткова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
9 |
|
22. |
Хомутинникова |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
9 |
|
23. |
Варакина |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
8 |
|
24. |
Прохорова |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
8 |
|
25. |
Чуракова |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
8 |
|
26. |
Ширяев |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
7 |
|
27. |
Кузнецов |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
6 |
|
28. |
Светлаков |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
|
Ранг задания |
28 |
28 |
28 |
25 |
23 |
23 |
22 |
21 |
21 |
19 |
17 |
16 |
13 |
284 |
|
|
Ранг трудности |
1 |
1 |
1 |
0,89 |
0,82 |
0,82 |
0,79 |
0,75 |
0,75 |
0,68 |
0,61 |
0,57 |
0,46 |
10,14 |
|
|
0,72 |
|||||||||||||||
Таблица №7.6. Показатель уровня качества в 5 «Е» классе
|
№ |
Фамилии учащихся |
∑ |
% качества |
Уровень качества |
|
1. |
Бровко |
13 |
100 |
Выше достаточного |
|
2. |
Галиева |
13 |
100 |
|
|
3. |
Зяблова |
13 |
100 |
|
|
4. |
Санатина |
13 |
100 |
|
|
5. |
Седнев |
13 |
100 |
|
|
6. |
Белоусов |
12 |
92 |
|
|
7. |
Бондаренко |
12 |
92 |
|
|
8. |
Горбачёв |
12 |
92 |
|
|
9. |
Карпова |
12 |
92 |
|
|
10. |
Салтыков |
12 |
92 |
|
|
11. |
Бабурина |
11 |
84 |
Достаточный |
|
12. |
Жемальдинов |
11 |
84 |
|
|
13. |
Федоренко |
11 |
84 |
|
|
14. |
Минина |
10 |
77 |
|
|
15. |
Муллоянов |
10 |
77 |
|
|
16. |
Новикова |
10 |
77 |
|
|
17. |
Широкова |
10 |
77 |
|
|
18. |
Банных |
9 |
69 |
|
|
19. |
Никулин |
9 |
69 |
|
|
20. |
Привалихина |
9 |
69 |
|
|
21. |
Снеткова |
9 |
69 |
|
|
22. |
Хомутинникова |
9 |
69 |
|
|
23. |
Варакина |
8 |
62 |
|
|
24. |
Прохорова |
8 |
62 |
|
|
25. |
Чуракова |
8 |
62 |
|
|
26. |
Ширяев |
7 |
54 |
Ниже достаточного |
|
27. |
Кузнецов |
6 |
46 |
|
|
28. |
Светлаков |
4 |
31 |
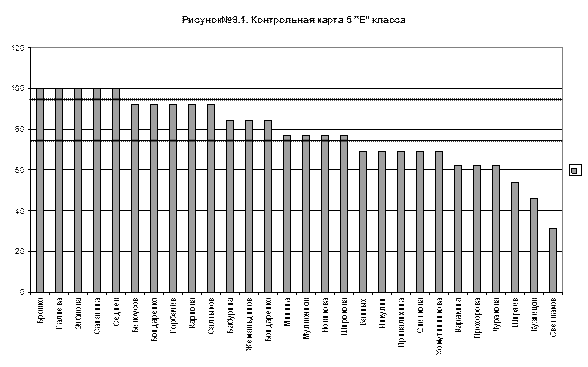
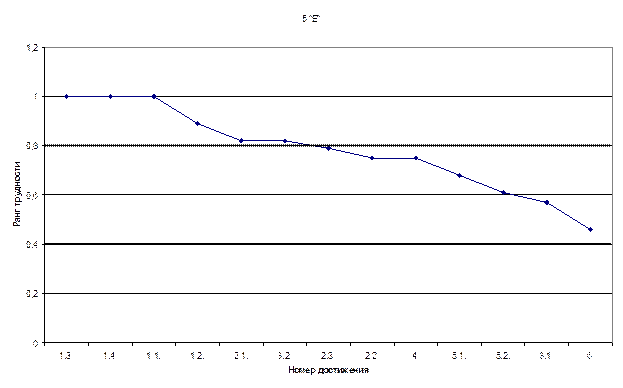
Таблица Структура уровня достижений 5 «Е» класса
|
Уровень качества |
Доля класса в % |
|
Выше достаточного |
36 % |
|
Достаточный |
53 % |
|
Ниже достаточного |
11 % |
Приложение 2
Анализ работ учащихся 5 «А» класса.
1. В классе 30 человек.
2. Писали работу 27 учеников.
3. В работе представлено 5 заданий. В соответствии со спецификацией денной работы мы можем говорить о том, что в ней представлены задания не выше аналитико-синтетического уровней. Так как все задания являются заданиями с открытым ответом, то поправку на угадывание мы можем не делать.
4. Максимальное количество баллов, которое можно набрать, верно выполнив все 5 заданий, составляет 16 баллов.
5. Найдём средний уровень группы.
Хср=12,3 баллов, что соответствует отметке «4»- хорошо.
6. Степень сложности работы.
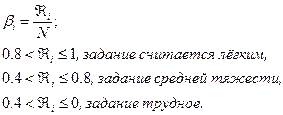
Так как средний уровень ранга трудности каждого задания составляет 0,78, то для данной группы учащихся контрольная работа оказалась средней трудности.
Таблица 2 - Е. Оценочная таблица 5 "Е" класса
|
№ |
Ф.И. учащихся |
1. |
2. |
3. |
4. |
5. |
6. |
7. |
8. |
9. |
10. |
11. |
12. |
13. |
14. |
15. |
∑ |
Отм |
|
1 |
Карпова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
16 |
5 |
|
2 |
Минина |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
16 |
5 |
|
3 |
Седнев |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
16 |
5 |
|
4 |
Снеткова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
16 |
5 |
|
5 |
Бондаренко |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
15 |
5 |
|
6 |
Горбачёв |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
2 |
15 |
5 |
|
7 |
Зяблова |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
15 |
5 |
|
8 |
Муллоянов |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
14 |
5 |
|
9 |
Белоусов |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
14 |
5 |
|
10 |
Банных |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
13 |
4 |
|
11 |
Федоренко |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
13 |
4 |
|
12 |
Бабарина |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
2 |
13 |
4 |
|
13 |
Жемальдинов |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
2 |
13 |
4 |
|
14 |
Галиева |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
13 |
4 |
|
15 |
Никулин |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
13 |
4 |
|
16 |
Санатина |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
12 |
4 |
|
17 |
Хомутинникова |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
13 |
4 |
|
18 |
Чуракова |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
12 |
4 |
|
19 |
Салтыков |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
11 |
4 |
|
20 |
Кузнецов |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
11 |
4 |
|
21 |
Широкова |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
11 |
4 |
|
22 |
Новикова |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
10 |
3 |
|
23 |
Прохорова |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
10 |
3 |
|
24 |
Привалихина |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
8 |
3 |
|
25 |
Варакина |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
8 |
3 |
|
26 |
Ширяев |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
8 |
3 |
|
27 |
Светлаков |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
4 |
2 |
|
Средний балл |
333 |
12,3 |
||||||||||||||||
7. В таблице № 1 рассмотрена спецификация работы. Учащийся набирает 1 балл за верно выполненный шаг, определённый для проверки, каждого задания базового, алгоритмического и аналитико-синтетического уровней и 2 балла за задание творческого уровня. Для определения ранга трудности каждого задания и рейтинга учащихся заменим в столбцах 1-14 показатели 0,5 и 0 на знак «0», в столбце 15 показатель 2 на знак «1», а показатели 1 и 0 на знак «0».
8. Вычислим размах. R = 15 – 4 = 11
Коэффициент вариации равен Кл = ![]()
Поэтому данный класс учащихся можно назвать как однородный класс.
9. Достижения учащихся представлены в таблицах 2 – Е и 3 – Е. Мы видим, что в данной группе учащихся нет таких, чей уровень достижений был бы выше допустимого, 26% учащихся показали допустимый результат и 74% - уровень ниже допустимого. Наглядное представление рейтингов учащихся показано на рисунке 1 – Е.
Таблица 3 - Е. Рейтинговая таблица 5 "Е" класса
|
№ |
Ф.И. учащихся |
1. |
9. |
7. |
2. |
13. |
14. |
11. |
12. |
8. |
5. |
3. |
4. |
10. |
6. |
15. |
∑ |
R |
УР |
|
1 |
Карпова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
15 |
1 |
ВД 41%
|
|
2 |
Минина |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
15 |
1 |
|
|
3 |
Седнев |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
15 |
1 |
|
|
4 |
Снеткова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
15 |
1 |
|
|
5 |
Бондаренко |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
14 |
0,9 |
|
|
6 |
Горбачёв |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
14 |
0,9 |
|
|
7 |
Зяблова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
14 |
0,9 |
|
|
8 |
Муллоянов |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
14 |
0,9 |
|
|
9 |
Белоусов |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
13 |
0,9 |
|
|
10 |
Банных |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
13 |
0,9 |
|
|
11 |
Федоренко |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
13 |
0,9 |
|
|
12 |
Бабурина |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
12 |
0,8 |
Д48% |
|
13 |
Жемальдинов |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
12 |
0,8 |
|
|
14 |
Галиева |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
12 |
0,8 |
|
|
15 |
Никулин |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
12 |
0,8 |
|
|
16 |
Санатина |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
12 |
0,8 |
|
|
17 |
Хомутинникова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
12 |
0,8 |
|
|
18 |
Чуракова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
12 |
0,8 |
|
|
19 |
Салтыков |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
11 |
0,73 |
|
|
20 |
Кузнецов |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
10 |
0,67 |
|
|
21 |
Широкова |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
10 |
0,67 |
|
|
22 |
Новикова |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
9 |
0,6 |
|
|
23 |
Прохорова |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
9 |
0,6 |
|
|
24 |
Привалихина |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
8 |
0,57 |
|
|
25 |
Варакина |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
8 |
0,53 |
НД 11% |
|
26 |
Ширяев |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
8 |
0,53 |
|
|
27 |
Светлаков |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
4 |
0,27 |
|
|
Рейтинг задания |
27 |
27 |
26 |
25 |
23 |
23 |
22 |
22 |
21 |
20 |
19 |
19 |
17 |
16 |
9 |
316 |
0,78 |
||
|
Ранг трудности |
1 |
1 |
0,96 |
0,93 |
0,85 |
0,85 |
0,81 |
0,81 |
0,78 |
0,74 |
0,7 |
0,7 |
0,63 |
0,59 |
0,33 |
11,7 |
|||
10. Анализ результатов выполнения каждого задания.
Ранг трудности каждого номера для данного класса представлен в таблице № 3-Е.
11. На рисунке № 2 - Е «Карта трудности Шухарта» мы видим, что не все задания, которые мы отнесли к базовому уровню, относятся к категории лёгких. Например, задание на вычитание смешанного числа из натурального относится к категории заданий средней трудности.
12. К наиболее типичным ошибкам относится деление десятичной дроби на натуральное число, отсутствие логики при решении задачи на движение, умение составить задачу по уравнению.
13. Сравним результаты работ учащихся на трёх контрольных измерениях: в мае 2005 года (итоговая контрольная работа за курс 4 класса), в ноябре 2005 года (контрольная работа по преемственности) и в апреле 2006 года. Данные по интересующим нас измерениям представлены в таблице 4 – Е.
![]()
![]()
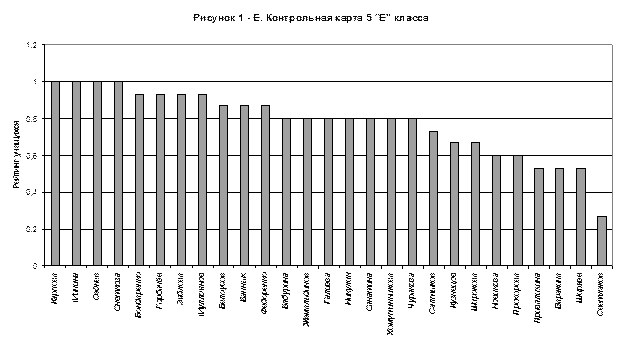
![]()
![]()
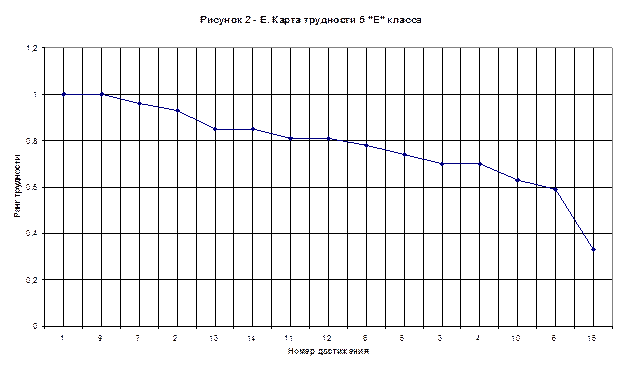
14. Анализ данных таблицы позволяет сделать вывод о наметившейся положительной тенденции в изменении уровня учебных достижений учащихся. Но повышение среднего уровня группы и соответственно средней отметки напрямую связано со степенью сложности работы. Коэффициент 0,78 показывает, что работа для учащихся оказалась средней трудности, и все проверяемые ЗУНы были усвоены учащимися на хорошем уровне.
15. Таблица 4 – Е. показывает, что однородность класса практически не изменилась, при этом увеличился показатель СОУ класса до 0,69. Отдельно надо отметить повышение граничных показателей уровней обученности учащихся. Несмотря на это процентное содержание уровней учебных достижений учащихся увеличивается до 41%.
Таблица 4 – Е. Сводный анализ достижений учащихся 5 "Е" класса в мае 2005 г., ноябре 2005 г. и апреле 2006 г.
|
Сравниваемые показатели |
Май 2015 года |
Ноябрь 2015 года |
Апрель 2016 года |
|
Количество учащихся |
30 |
30 |
30 |
|
Писали работу |
29 |
28 |
27 |
|
Максимальный балл |
13 |
13 |
16 |
|
Средний уровень группы |
10,58 |
10,14 |
12,3 |
|
Средняя отметка |
хорошо |
хорошо |
хорошо |
|
Степень сложности работы |
0,71 |
0,73 |
0,78 |
|
Выше допустимого |
39% |
36% |
41% |
|
Граничный показатель |
0,9 |
0,9 |
0,9 |
|
Допустимый |
48% |
53% |
48% |
|
Граничный показатель |
0,55 |
0,55 |
0,55 |
|
Ниже допустимого |
13% |
11% |
11% |
|
Размах |
10 |
9 |
11 |
|
Однородность |
0,89 – одн. |
0,89 –однородный |
0,89 – однородный |
|
СОУ |
0,61 |
0,59 |
0,69 |
16. Рассматривая рейтинг каждого учащегося на двух контрольных измерениях, мы введём такой показатель успешности ребёнка, как изменение рейтинга (∆R). Положительное значение ∆R свидетельствует о росте уровня учебных достижений учащегося, отрицательное же его значение говорит об обратном. Из данных таблицы 5 – Е «Сравнительная таблица рейтинга учащегося» видно, что 14 учеников имеет отрицательный ∆R, это составляет 51% учащихся, выполнивших работу, при этом только 5 учащихся имеют отклонение, большее 0,15 (17%) . Значимое положительное отклонение имеет 17% учащихся.
Таблица 4 - Е. Сравнительная таблица рейтинга учащихся
|
№ |
Ф.И. учащегося |
Ноябрь |
Апрель |
∆R |
|
1 |
Бровко |
1 |
н |
0 |
|
2 |
Галиева |
1 |
0,8 |
-0,2 |
|
3 |
Зяблова |
1 |
0,93 |
-0,07 |
|
4 |
Санатина |
1 |
0,8 |
-0,2 |
|
5 |
Седнев |
1 |
1 |
0 |
|
6 |
Белоусов |
0,92 |
0,87 |
-0,05 |
|
7 |
Бондаренко |
0,92 |
0,93 |
0,01 |
|
8 |
Горбачёв |
0,92 |
0,93 |
0,01 |
|
9 |
Карпова |
0,92 |
1 |
0,08 |
|
10 |
Салтыков |
0,92 |
0,73 |
-0,19 |
|
11 |
Бабурина |
0,84 |
0,8 |
-0,04 |
|
12 |
Жемальдинов |
0,84 |
0,8 |
-0,04 |
|
13 |
Федоренко |
0,84 |
0,87 |
0,03 |
|
14 |
Минина |
0,77 |
1 |
0,23 |
|
15 |
Муллоянов |
0,77 |
0,93 |
0,16 |
|
16 |
Новикова |
0,77 |
0,6 |
-0,17 |
|
17 |
Широкова |
0,77 |
0,67 |
-0,1 |
|
18 |
Банных |
0,69 |
0,87 |
0,18 |
|
19 |
Никулин |
0,69 |
0,8 |
0,11 |
|
20 |
Привалихина |
0,69 |
0,53 |
-0,16 |
|
21 |
Снеткова |
0,69 |
1 |
0,31 |
|
22 |
Хомутинникова |
0,69 |
0,8 |
0,11 |
|
23 |
Варакина |
0,62 |
0,53 |
-0,09 |
|
24 |
Прохорова |
0,62 |
0,6 |
-0,02 |
|
25 |
Чуракова |
0,62 |
0,8 |
0,18 |
|
26 |
Ширяев |
0,54 |
0,53 |
-0,01 |
|
27 |
Кузнецов |
0,46 |
0,67 |
0,21 |
|
28 |
Светлаков |
0,31 |
0,27 |
-0,04 |
|
|
|
|
|
0,24 |

|
Бровко
|
Галиева |
Зяблова |
Санатина |
Седнев |
Белоусов |
Бондаренко |
Горбачёв |
Карпова |
Салтыков |
Бабурина |
Жемальдинов |
Федоренко |
Минина |
Муллоянов |
Новикова |
Широкова |
Банных |
Никулин |
Привалихина |
Снеткова |
Хомутинникова |
Варакина |
Прохорова |
Чуракова |
Ширяев |
Кузнецов |
Светлаков |
Приложение 3
Анализ результатов
контрольной работы по математике
6 «А» класс
Учитель: Пермякова Светлана Николаевна
Х ср = 14,29 балла, что соответствует отметке «4» - хорошо.
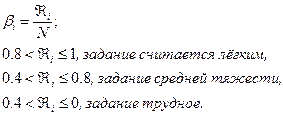
Так как средний уровень ранга трудности каждого задания составляет 0,75, то для данной группы учащихся контрольная работа оказалась средней трудности.
R = 18 – 3 = 15
Поэтому данный класс учащихся можно назвать как класс не однородный.
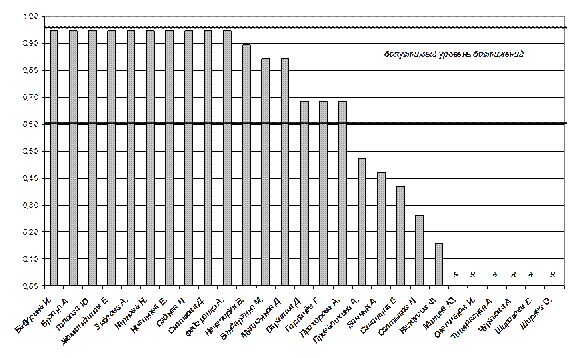
Рисунок 1 Контрольная карта 6Е класса по математике
Ранг трудности каждого номера для данного класса представлен в таблице № 26.
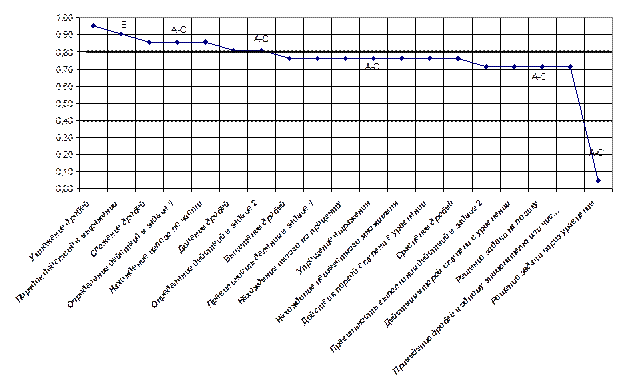
Рисунок 2 Карта трудности 6Екласса по математике
Таблица 7 Сводный анализ достижений учащихся
|
Сравниваемые показатели |
Ноябрь 2005 года |
Апрель 2006 года |
Январь 2007 года |
|
Количество учащихся |
30 |
30 |
27 |
|
Писали работу |
28 |
27 |
21 |
|
Максимальный балл |
13 |
16 |
16 |
|
Средний уровень группы |
10,14 |
12,3 |
14,29 |
|
Средняя отметка |
хорошо |
хорошо |
Хорошо |
|
Степень сложности работы |
0,73 |
0,78 |
0,75 |
|
Выше допустимого |
36% |
15% |
0% |
|
Граничный показатель |
0,9 |
0,95 |
0,95 |
|
Допустимый |
53% |
70% |
76% |
|
Граничный показатель |
0,55 |
0,6 |
0,6 |
|
Ниже допустимого |
11% |
15% |
24% |
|
Размах |
9 |
11 |
15 |
|
Однородность |
0,89 –однородный |
0,89 - однородный |
1,05 – не однородный |
|
СОУ |
0,59 |
0,66 |
0,73 |
Таблица 8 Сравнительная таблица рейтинга учащихся 6А класса по математике
|
№ |
Ф.И. учащегося |
Ноябрь |
Апрель |
Январь |
∆R |
|
1 |
Бабурина |
0,84 |
0,8 |
0,95 |
0,15 |
|
2 |
Бровко |
1 |
0 |
0,95 |
-0,05 |
|
3 |
Галиева |
1 |
0,8 |
0,95 |
0,15 |
|
4 |
Жемальдинов |
0,84 |
0,8 |
0,95 |
0,15 |
|
5 |
Зяблова |
1 |
0,93 |
0,95 |
0,02 |
|
6 |
Карпова |
0,92 |
1 |
0,95 |
-0,05 |
|
7 |
Новикова |
0,77 |
0,6 |
0,95 |
0,35 |
|
8 |
Седнев |
1 |
1 |
0,95 |
-0,05 |
|
9 |
Снеткова |
0,69 |
1 |
0,95 |
-0,05 |
|
10 |
Федоренко |
0,84 |
0,87 |
0,95 |
0,08 |
|
11 |
Нечепорук В. |
|
0,7 |
0,89 |
0,19 |
|
12 |
Бондаренко |
0,92 |
0,93 |
0,84 |
-0,09 |
|
13 |
Муллоянов |
0,77 |
0,93 |
0,84 |
-0,09 |
|
14 |
Варакина |
0,62 |
0,53 |
0,68 |
0,15 |
|
15 |
Горбачёв |
0,92 |
0,93 |
0,68 |
-0,25 |
|
16 |
Прохорова |
0,62 |
0,6 |
0,68 |
0,08 |
|
17 |
Привалихина |
0,69 |
0,53 |
0,47 |
-0,06 |
|
18 |
Банных |
0,69 |
0,87 |
0,42 |
-0,45 |
|
19 |
Санатина |
1 |
0,8 |
0,37 |
-0,43 |
|
20 |
Салтыков |
0,92 |
0,73 |
0,26 |
-0,47 |
|
21 |
Белоусов |
0,92 |
0,87 |
0,16 |
-0,71 |
|
22 |
Минина |
0,77 |
1 |
0,00 |
0,23 |
|
23 |
Светлаков |
0,31 |
0,27 |
0,00 |
-0,04 |
|
24 |
Тишковская А. |
|
|
0,00 |
0,00 |
|
25 |
Чуракова |
0,62 |
0,8 |
0,00 |
0,18 |
|
26 |
Широкова |
0,77 |
0,67 |
0,00 |
-0,10 |
|
27 |
Ширяев |
0,54 |
0,53 |
0,00 |
-0,01 |
|
|
|
|
|
|
-0,04 |
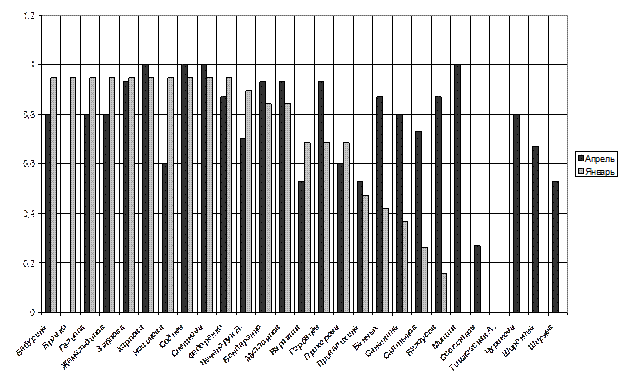
Рисунок 3 Сравнение рейтингов на двух контрольных измерениях
Рисунок 4 Изменение рейтинга учащихся 6Д класса по математике.
Рисунок 5 Прогноз изменения среднего рейтинга учащихся 6Е класса
Таблица 9
Количественные и качественные показатели результатов работы в 6Е классе
|
Всего |
Писали |
"5" |
"4" |
"3" |
"2" |
СОУ |
К |
|
27 |
21 |
11 |
5 |
2 |
3 |
0,73 |
0,76 |
Выводы и рекомендации учителю:
Приложение 4.Диагностика «Цветометодика: моё настроение на уроке»Применение данной диагностики позволяет изучить отношение учащихся класса к предмету. Для проведения исследования учащимся предлагают заполнить бланк для ответов, внимательно прочитав возможные ситуации на уроках и различные оттенки настроения.Анализ приведённых диаграмм позволяет сделать вывод о положительном отношении учащихся исследуемой группы к урокам математики. На уроке учащиеся испытывают спокойствие, удовлетворённость, энергичность, собранность, деловое настроение, чувствуют себя совершенно свободно, уверены в себе, им хорошо.Низкий рейтинг ситуации во время объяснения нового материала говорит о том, что учащиеся привыкли к продуктивной деятельности на уроках, самостоятельному изучению нового материала, решению проблемных ситуаций. Значительная разница между ответами с места и у доски говорит в пользу высокого уровня развития коммуникативных компетенций. Мы так же видим высокие показатели настроения в ситуациях самостоятельной работы и при решении нестандартных и трудных задач.
Бланк ответов_____________________________________________________________5 «_______» класс 2015 – 2016 учебный год
|
№ |
Ситуация на уроке |
Предметы |
|||||||||||
|
Русский язык |
Литература |
Словесность |
Математика |
История |
Природоведение |
Английский |
ИЗО |
Музыка |
Физкультура |
Труд |
ОБЖ |
||
|
1. |
Иду на урок. |
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Слушаю объяснение учителя. |
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Учитель дал самостоятельную работу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
Отвечаю у доски. |
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Отвечаю с места. |
|
|
|
|
|
|
|
|
|
|
|
|
|
6. |
Учитель дал трудную, нестандартную задачу. |
|
|
|
|
|
|
|
|
|
|
|
|
|
7. |
Учитель объявляет отметки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
Учитель обратил на меня внимание, разговаривает со мной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
9. |
Завтра контрольная. |
|
|
|
|
|
|
|
|
|
|
|
|
КЛЮЧ
|
Оттенки настроения |
Цвет |
Балл |
Оттенки настроения |
Цвет |
Балл |
|
Я спокоен |
Зелёный |
+1 |
Мне всё равно |
Серый |
0 |
|
Я удовлетворён |
Зелёный |
+1 |
Я не уверен в себе |
Серый |
0 |
|
Я энергичен, собран |
Зелёный |
+1 |
Я напряжен |
Серый |
0 |
|
Обычное деловое настроение |
Зелёный |
+1 |
Я погружен в свои мысли |
Серый |
0 |
|
Чувствую себя совершенно свободно |
Зелёный |
+1 |
Мне скучно |
Серый |
0 |
|
Мне радостно |
Красный |
+2 |
Я волнуюсь, настороже |
Коричневый |
-1 |
|
Подъём настроения |
Красный |
+2 |
Я раздражен, испытываю чувство досады |
Коричневый |
-1 |
|
Уверен в себе |
Красный |
+2 |
Чувство страха |
Чёрный |
-2 |
|
Мне хорошо |
Красный |
+2 |
Мне хочется ударить кулаком по столу, закричать |
Чёрный |
-2 |
Приложение 5 Лист самоконтроля. По окончании каждого урока в изучаемом блоке просим дать самооценку (с/о) степени понимания изученного материала. Используйте следующие критерии:· В материале разобрался(ась), на уроке было интересно - 3 балла.
· Мне все понятно, но материал не всегда интересен - 2 балла.
· Мне хотелось разобраться, но я не все понял(а) - 1 балл.
· Материал трудный и малоинтересный. Мало что понял(а) - 0 баллов.
Ур.1 |
Ур.2 |
Ур.3 |
Ур.4 |
Ур.5 |
Общая с\о по блоку |
|
|
|
|
|
|
Оценочный лист. Портфолио.
Ф.И. ученика |
Критерии |
Окончательная оценка |
||
|
|
|
||
1. |
|
|
|
|
2. |
|
|
|
|
Оценка работы группы № ____________
Вопросы |
Ваши впечатления |
Отличившиеся |
Хорошо ли вам работалось в группе? С кем особенно хорошо и почему? |
|
|
Удавалось ли вам договориться друг с другом?Все ли слушали друг друга? Кто в большей степени проявлял культуру диалога? |
|
|
Все ли члены группы принимали равноценное участие в работе группы? Кто в большей степени проявил себя, и кто не проявил себя никак? |
|
|
Всю ли работу, предложенную группе, удалось выполнить? |
|
|
Что считаете основным достижением группы? Кого бы хотели особенно отметить и за что? |
|
|
Какие были трудности в работе группы? Кто, на ваш взгляд, мог сделать больше? |
|
|
Ваша оценка работе группы? |
|
|
Приложение 6Новый подход к обеспечению качества образования Регулирование «выхода» системы Приложение 7
Предметные компетенции учителя.
Одним из факторов, определяющих качество образования, является содержание предметных компетенций учителя. Они представляют собой педагогическую адаптированную систему:
· научных знаний;
· способов деятельности (умения действовать по образцу);
· опыта творческой деятельности в форме умения принимать эффективные решения в проблемных ситуациях;
· опыта эмоционально-ценностного отношения к природе, обществу и человеку.
Очевидно, что составляющие профессионально-педагогической компетентности учителей различных учебных дисциплин будут иметь определенные доминанты, что обусловлено спецификой предмета и методикой его преподавания.
Представим вашему вниманию некоторые предметные компетенции учителя.
Компетенции по математике
· базовые математические приемы, алгоритмы измерений
· математический язык
· самостоятельная познавательная деятельность, основанная на усвоении способов приобретения математических знаний из различных источников информации
· математическая грамотность, т.е. необходимость вырабатывать у школьников способность определять и понимать роль математики в мире, в котором они живут; высказывать хорошо обоснованные математические суждения
· вырабатывать у учащихся умения применять математические знания и навыки в нестандартных ситуациях, умения, которые будут способствовать успешности выпускника во взрослой жизни
ЛитератураСловари1. Безрукова В.С. Словарь нового педагогического мышления. Екатеринбург, 1992.
2. Советский энциклопедический словарь, М. - "Советская энциклопедия", 1987.
1. 5 ключевых компетенций: (из доклада зам. директора Департамента образования, культуры и спорта Совета Европы М.Стобарта)
2. Бермус А.Г. «Проблемы и перспективы реализации компетентностного подхода в образовании» Интернет-журнал «Эйдос». 2003
3. Бондаревская Е.В. , Кульневич С.В. Парадигмальный подход к разработке ключевых педагогических компетенций. // Педагогика - М., №10 С.23-31.
4. Бородай Ю. "Почему православным не годится протестантский капитализм". Ж. "Наш современник" №10, 1990.
5. Голуб Г.Б., Чуракова О.В. Попытка определения компетенции как образовательного результата.
6. Государственный образовательный стандарт.
7. Гордон Л.А. Социальная адаптация в современных условиях. Социол. исслед. № 8, 9. 1994.
8. Гришанова Н.А. Компетентностный подход в обучении взрослых: Материалы к третьему заседанию методологического семинара 28 сентября 2004 г. – М.: Исследовательский центр проблем качества подготовки специалистов, 2004. – 16 С.
9. Джемс У. "Прагматизм". Спб., 1910. стр. 150.
10. Зеер Э.Ф., Павлова А.М., Сыманюк Э.Э. модернизация профессионального образования: компетентностный подход. – М.: Московский психолого-социальный институт, 2005.
11. Зимняя И.А. Ключевые компетентности как результативно-целевая основа компетентностного подхода в образовании. Авторская версия. – М.: Исследовательский центр проблем качества подготовки специалистов, 2004.
12. Иванов Д. А., Митрофанов К. Г., Соколова О. В. "Компетентностный подход в образовании. Проблемы, понятия, инструментарий" Учебно-методическое пособие. Академия АПК и ПРО. М. 2003.
13. Иванов Д. А. "Экспертиза в образовании: краткое содержание основных понятий, терминов и подходов" Учебно-методическое пособие. Академия АПК и ПРО. М. 2003.
14. Кальней В.А., Шишов С.Е. Технология мониторинга качества обучения в системе «учитель-ученик». Метод. пособие для учителя. М.: Педагогическое общество России, 1999. – 86 с.
15. Ковалева Г.С. Пути реализации стратегических целей обновления школы, -М., 2000.
16. Концепция модернизации российского образования на период до 2010 года. – М., 2002.
17. Лазарев В.С. Системное развитие школы. - М., 2002. - 304 с.
18. Материалы РГПУ им. А.И. Герцена по осуществлению компетентностного подхода в образовательном процессе.
19. Маркова А.К. Психология профессионализма. – М., 1996.
20. Маркова А.К. Психология труда учителя. М., 1993.
21. Методические материалы по психолого-педагогическому обеспечению процесса адаптации учащихся 5-х классов в средней школе (по материалам работы сотрудников лаборатории прикладной педагогической психологии)/ М-во образования Респ. Беларусь. Акад. последиплом. образования. -Минск,1998. - 25 с.
22. Пермякова С.Н. Роль мониторинга качества образования в успешности адаптации школьников во время перехода на основную ступень обучения.// Управление качеством образования: проблемы непрерывного образования: Сборник научных статей V международной научно-практической конференции: В 2 ч. Ч. I. Пленарные и секционные доклады. 4-5 апреля 2006 года/ Под науч. Ред. А.А. Симонова и др.- Екатеринбург: ГОУ ВПО «УрГПУ», 2006.-363 с.
23. Пермякова С.Н. Ключевые компетенции и компетентность младшего школьника как условие успешности ученика в период адаптации при переходе на 2 ступень школьного образования.//Компетентностный подход в образовании: достижения, проблемы и опыт образовательной практики Екатеринбурга: Сборник научных статей XII педагогических чтений работников системы образования Екатеринбурга.- Екатеринбург: ГОУ ВПО «УрГПУ», 2006. – 372 с.
24. Психология под ред. А.А. Крылова, М. - "Проект", 1998.
25. Розенберг Н.М. Проблемы измерений в дидактике. Киев, 1979.
26. Сериков В.В. Теория и практика проектирования образовательных систем. - М., 1999.
27. Симонов В.П. Педагогический менеджмент: 50 ноу-хау в области управления образовательным процессом: Учеб пособие. - М., 1997
28. Скок Т.Б. Как проанализировать собственную педагогическую деятельность, М., 2000
29. Спиркин А.Г. Основы философии. М., 1988. С. 237.
30. Стратегия модернизации содержания общего образования. Материалы по разработке документов по обновлению общего образования. – М., 2001.
31. Фирсов М.В., Студенова Е.Г. Теория социальной работы: Учеб. пособие для студ. высш. учеб. заведение. – М.: Гуманит. изд. центр ВЛАДОС, 2001
32. Хуторской А.В. Ключевые компетенции как компонент личностно-ориентированной парадигмы образования. // Народное образоание - М., 2003 №2 .С. 55-61.
33. Хуторской А.В. Ключевые компетенции и образовательные стандарты. Доклад на отделении философии образования и теории педагогики РАО 23 апреля 2003. Центр «Эйдос» www.eidos. ru /news/ compet. htm.
34. Чепурных. Е. Е. "Воспитание в системе образования на пороге XXI века". Доклад на Всероссийской конференции "Мировой опыт организации и реализации воспитания" 03.04.2000г. В сб. "Инновации в российском образовании". М. Изд-во МГПУ, 2000.
35. Яковлев Е.В. Квалиметрический подход в педагогическом исследовании: новое видение. Педагогика. 1999. №3 С. 49 – 54.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.