Рекомендации по выполнению домашней контрольной работы по теме "Векторы"

Домашняя  контрольная работа по теме векторы

Рекомендации к выполнению

1.                 Работу необходимо выполнить в тетради в клетку синими чернилами. Допускается применение разноцветных чернил (кроме красного цвета) для выделения формул  и основных понятий.  Необходимо оставлять поля для замечаний.

2.                 При выполнении работы нужно следить за аккуратностью записей и чертежей. Чертежи выполняются строго карандашом и по линейке.

3.                 Перед выполнением практической части работы,  нужно  изучить теоретические вопросы, используя рекомендуемую литературу.

4.                 После ответов на вопросы выполняется практическая часть работы.

5.                 Вариант выполняемого задания соответствует  порядковому номеру студента  в журнале.

6.                 При выполнении  работы студент может обращаться к преподавателю за консультацией.

7.                 Задания отмеченные (*) относятся к повышенному уровню сложности.

Векторы

Вопросы и задания:
Что называется: вектором, равными векторами, коллинеарными векторами, компланарными векторами, суммой векторов, произведением вектора на число, разностью векторов, координатами вектора в базисе, скалярным произведением векторов, векторным произведением векторов, смешанным произведением векторов, уравнение лини в декартовой системе координат, направляющий и нормальный вектор, расстояние от точки до прямой (плоскости).

Перечислить свойства: суммы векторов, произведением вектора на число, скалярного произведения векторов, векторного произведения  векторов, смешанного произведения векторов.

Сформулировать необходимое и достаточное условие: коллинеарности векторов, ортогональности векторов, компланарности векторов.

Записать  в координатной форме: линейную комбинацию векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение векторов.

Записать формулы: для вычисления косинуса угла между векторами, площади параллелограмма, построенного на векторах, как на сторонах, объема параллелепипеда, построенного на трех векторах, косинуса угла между прямыми, тангенса угла между прямыми; для составления уравнения прямой, проходящей через две (три) точки, уравнения плоскости, проходящей через три точки, расстояния от точки до плоскости.

Изучить^*: порядок вычисления определителя первого и второго порядка

Контрольная работа по теме «Векторы»

1-10. Даны вершины треугольника. Постройте чертеж данной фигуры и найдите:

a.     Уравнение стороны АС

b.     Уравнение высоты, проведенной из вершины В

c.     Длину высоты, проведенной из вершины А

d.     Величина угла В

1.     А (5; 3),    В (-11; -9),   С (-4; 15)

2.     А (-7; 2),   В (5;  -3),     С (8; 1)

3.     А (1; 15),  В (6; -3),    С (2; 0)

4.     А (-8; 3),   В (4; -2),    С (7; 2)

5.     А (6; 3),    В (-10; -9),   С (-3; 15)

6.     А (-9; 6),   В (3; 1), С (6, 5)

7.     А (20; 5),  В (-4; 12),  С (-8; 9)

8.     А (-3; -7),  В (2; 5),  С (-2; 8)

9.     А (10; 1),   В (-6; 13),  С (1; -11)

10. А (0; -9),    В (5; 3),    С (1; 6).

2-20.     Даны вершины пирамиды. Постройте фигуру и средствами векторной алгебры найдите:

a.     Длину ребра АВ

b.    Угол между ребрами АВ и АС

c.     ^* Площадь грани АВС

d.    Длину высоты  пирамиды, проведенной из вершины D

e.     ^* Объем пирамиды ABCD

1.     A (7; 0; 3),   B (3; 0; -1),  C (3; 0; 5),  D (4; 3; -2)

2.     A (1; -1; 6),  B (2; 5; -2),  C (3; 3; 3),  D (4; 1;5)

3.     A (3; 6; 1),   B (6; 1;4),  C (3; -6; 10),  D (7; 5; 4)

4.     A (1; 1; 3),  B (6; 1; 4),  C (6; 4; 1),  D (0; 5; 6)

5.     A (4; 4; 5),  B (10; 2; 3),  C (-3; 5; 4),  D (6; -2; 2)

6.     A (-1; 2; 5), B (-4; 6; 4),  C (2; 1; 5),  D (-1; -2; 2)\

7.     A (2; -1; 9),   B (1; 1; 5),  C (7; 3; 1),  D (2; 6; -2)

8.     A (1; -2; 2),   B (-1; -3; 4),  C (5; 5; -1),  D (2; -4; 5)

9.     A (1; 1; 3),    B (7; 1; 1),  C (2; 2; 2),  D (4; 1; -1)

10. A (3; 1; 2),   B (5; 0; -1),  C (0; 3; 6),  D (3; 7; 10) 

Пример решения задач контрольной работы

1. Даны вершины треугольника А (5; 1),  В (1; -3), С (-1; -1). Постройте чертеж данной фигуры и найдите:

a.     Уравнение стороны АС

b.     Уравнение высоты, проведенной из вершины В

c.     Длину высоты, проведенной из вершины А

d.     Величина угла В

Решение:

 a)   Уравнение прямой, проходящей через две известные точки  М₁ (x₁; y₁), М₂ (x₂; y₂) имеет вид:

поэтому уравнение прямой (АС)  примет вид:

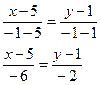  направляющий вектор данной прямой  .

Преобразуем данное уравнение

b) Высота из вершины В проводится к стороне АС, поэтому направляющий вектор прямой (АС) будет нормальным вектором  высоты, проходящей через точку В. Уравнение прямой проходящей через точку М₁ (x₁; y₁) с нормальным вектором  имеет вид:

Высота проходит через точку В (1; -3) и нормальный вектор , поэтому 

с)  Величину высоты, проведенной из точки М₁(x₁; y₁) к прямой Ax+By+C=0, можно найти по формуле:  

Чтобы найти величину высоты, проведенной  из точки А к стороне ВС, нужно знать уравнение прямой (ВС):

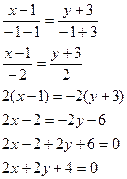
d)  Для определения угла В воспользуемся формулой тангенса угла между двумя прямыми, имеющими угловые коэффициенты k₁, k₂:  

Уравнение прямой (АВ)

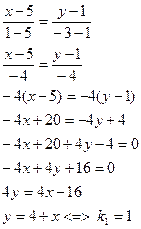
Уравнение прямой (ВС)

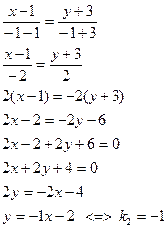
2. Даны вершины пирамиды A (1; 2; 3),  B (7; 10; 3), C (-1; 3; 1), D (8; 8; 8). Постройте фигуру и средствами векторной алгебры найдите:

a.    Длину ребра АВ

b.    Угол между ребрами АВ и АС

c.     Площадь грани АВС

d.    Длину высоты  пирамиды, проведенной из вершины D

e.     Объем пирамиды ABCD

Решение:

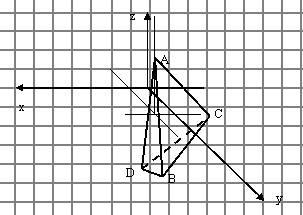Построение пирамиды:

1. провести прямую, параллельную оси ОY,   через точку  на оси ОХ с координатами (1, 0, 0).

2. провести прямую, параллельную  оси ОХ, через точку на оси ОY с координатами (0, 2, 0).

3. Через точку пересечения этих прямых провести прямую, параллельную оси OZ.

4. Отложить на этой прямой три единицы вверх, получаем точку А.

5. Аналогично построить остальные точки. Соединить все точки.

6. Получаем пирамиду ABCD.

a.     Длину ребра АВ найдем как длину вектора по формуле:

b.    Угол между ребрами АВ и АС найдем как угол между векторами по формуле:

Найдем координаты векторов по формуле

c.     Площадь грани АВС можно вычислить по формуле: , где  - векторное произведение векторов.

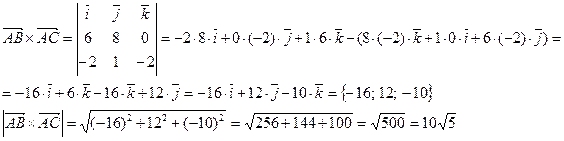
d.    Длину высоты  пирамиды, проведенной из вершины D к плоскости АВС воспользуемся формулой расстояния от точки до плоскости:

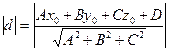
 Составим уравнение плоскости АВС по формуле: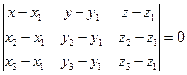  

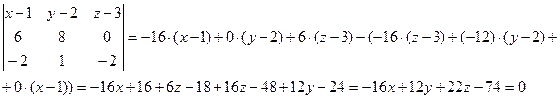
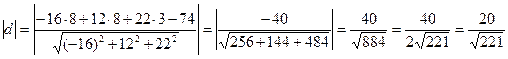
e.     Объем пирамиды ABCD вычислим по формуле:

, где  - смешанное произведение векторов.

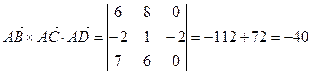
Рекомендуемая литература

1.    Башмаков М.И. Математика: учебник для 10 кл.: среднее (полное) общее образование / М.И. Башмаков.-М.: Издательский центр «Академия», 2006. – 304с.

2.    Валуцэ И.И. Математика для техникумов  на базе средней школы: учебное пособие/ И.И. Валуцэ - М.: Наука 1989.- 576с.

3.    Данко П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1: учебное пособие для вузов/ П.Е. Данко – М.: ООО «Издательство Оникс»: ООО «Издательство «Мир и Образование», 2009. – 368с.

4.    Высшая математика для экономистов: учебник для вузов/под редакцией проф. Н.Ш. Кремера. – М. ЮНИТИ, 2002. – 471с.

5.    Малахов А.Н. Высшая математика: учебное пособие, руководство по изучению дисциплины. – МЭСИ, 2007. – 360с.

Скачано с www.znanio.ru