Рекурсия.

Рекурсия.

В предыдущем разделе данного пособия мы уже рассматривали программу, в которой имеется процедура, содержащая обращения к другим процедурам. Обращения к другим функциям и процедурам могут содержать и функции. При этом возможен и такой вариант, когда какая-либо функция или процедура содержит обращение к самой себе. Такая функция или процедура называется рекуррентной (от английского слова «recurrence», что в переводе означает возвращение или повторение), а процесс вызова функции или процедуры из нее самой – рекурсией.

Процесс рекурсии происходит следующим образом: в начале происходит вызов некоторой функции(процедуры). Затем, еще до завершения своей работы, эта же функция(процедура) вызывает саму себя, и в результате в памяти компьютера появляется второй экземпляр той же функции(процедуры), второй экземпляр в ходе работы создает третий, и так далее. Естественно, что такой процесс может продолжаться до бесконечности, поэтому для решения какой-либо конкретной задачи в рекурсивной функции(процедуре) обязательно должен содержаться условный оператор, одна из ветвей которого обеспечивает прерывание этой бесконечной цепочки и завершение работы всех экземпляров функции (процедуры). Внутри этого оператора и должен находиться вызов функции.

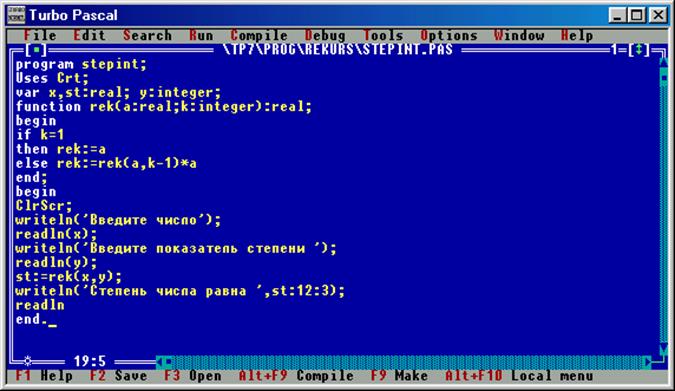
В качестве несложного примера, наглядно иллюстрирующего процесс рекурсии, рассмотрим задачу вычисления целой положительной степени вещественного числа (x^y) (см. рис. 30). В данной программе в основной ее части производится только ввод исходных данных (самого числа x и показателя степени y), вызов рекурсивной функции rek и вывод полученного

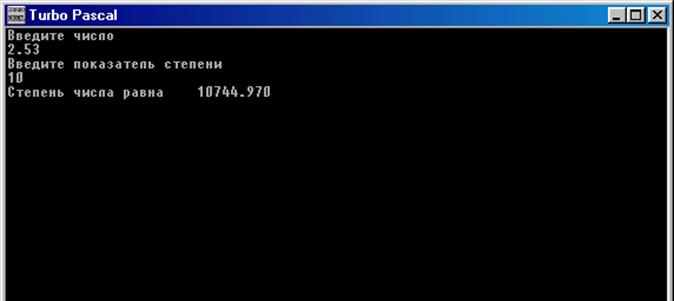Рис.   30.      Программа   вычисления   целой                   положительной степени вещественного числа и результат ее работы.

результата, а само вычисление степени производится в функции rek. Разберем более подробно механизм действия данной функции.

Для этого нужно ответить на вопрос : чему равно любое число в первой степени. Ответ очевиден – самому этому числу. Это мы и запишем в начале условного оператора: для k=1 результат rek равен исходному числу a. Для нахождения же квадрата числа нужно это число умножить само на себя, для нахождения куба – квадрат числа умножить на это число и так далее. Таким образом, существует следующая закономерность k степень числа равна этому числу в степени k-1, умноженному на само число:

ak=a(k-1)*a

Эту формулу запишем в той ветви условного оператора, которая находится после служебного слова else.

Теперь рассмотрим непосредственно работу функции. Данная функция имеет два формальных параметра a и k, которым соответствуют в основной части программы фактические параметры x и y. Значением функции является a^k

. Для вычисления значения функции rek с параметрами k и a вызывается другой экземпляр той же функции с параметрами k-1 и a (a остается неизменным для всех экземпляров функции), затем этот экземпляр вызывает следующий с параметром k-2 и так далее, пока процесс не доходит до обращения к экземпляру для k=1. Значение функции для k=1 уже известно, оно передается в экземпляр для k=2 и так далее, пока не определяется значение для

k. Это последнее значение передается в основную часть программы для вывода на экран компьютера.

На рис. 30 приведен результат работы программы для x=2,53 и y=10.

В заключение данной главы приведем еще один пример использования

рекурсии   для решения классической математической задачи известной как

«числа  Фибоначчи».  Эта  задача  была  решена  в   XIII   веке              выдающимся итальянским   математиком       Леонардо    Фибоначчи.              Вот   ее           условия:       пара

кроликов каждый месяц дает потомство - двух кроликов, которые через два

месяца сами способны давать новое потомство. Сколько кроликов будет через год, если в начале года была одна пара кроликов.

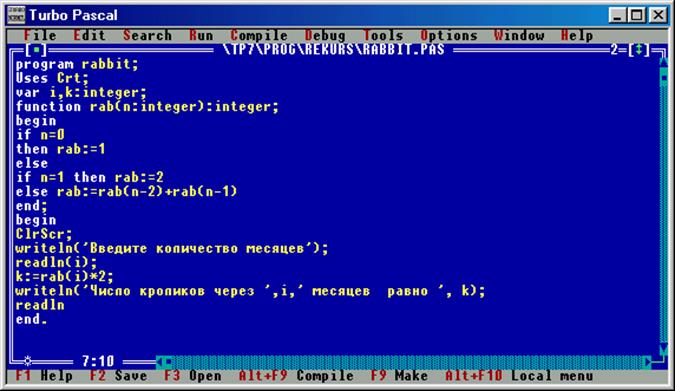
Для решения данной задачи используем рекурсивную функцию rab(n), которая определяет количество пар кроликов через n месяцев после начала года. В начале года существовала только одна пара кроликов, то есть rab(0)=1, через месяц их стало две, следовательно rab(1)=2. Через 2 месяца количество пар кроликов увеличивается еще на 1, то есть на столько, сколько их было в

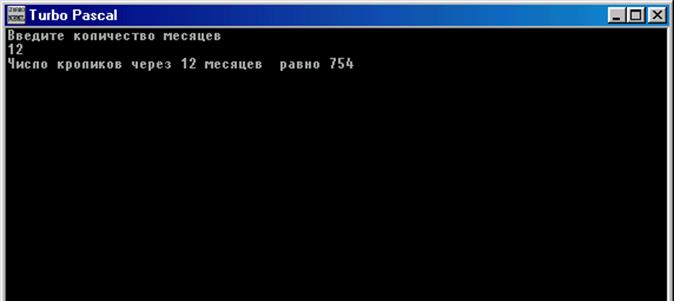Рис. 31 Программа «числа Фибоначчи» и результаты ее работы.

начале года. Таким образом rab(2)=3 или rab(2)=rab(1)+rab(0). Продолжая наши рассуждения, получаем следующую зависимость:

rab(n)=rab(n-1)+rab(n-2)

Эту    рекурсивную   функцию    используем   в    программе   rabbit,          которая подсчитывает и выводит на экран количество кроликов через n месяцев.

Количество кроликов через n месяцев будет равно rab(n)*2. Ниже приведены результаты работы программы при n=12, то есть искомое количество кроликов через год.