
Решение практико-ориентированных задач при подготовке к ОГЭ и ЕГЭ по математике
Основная идея обновления средней и старшей ступени школы состоит в том, что общее образование приобретает профессионально-ориентированное содержание. Ставится задача создания системы предпрофильного и профильного обучения, ориентированной на индивидуализацию обучения и социализацию учащихся с учетом реальных потребностей рынка, отработки гибкой системы профилей, и интеграции старшей ступени школы с учреждениями начального, среднего и высшего профессионального образования.
Переход к профильному обучению направлен на реализацию одновременно принципов личностно-ориентированного и практико-ориентированного образования, поэтому он преследует широкие образовательные и развивающие цели:
• подготовку и сдачу ОГЭ и ЕГЭ учащихся;
обеспечение углубленного изучения отдельных предметов;
• создание условий для дифференциации содержания
обучения старшеклассников с широкими возможностями для построения
индивидуальных образовательных траекторий;
• обеспечение равного доступа к полноценному образованию разных категорий
обучающихся в соответствии с их способностями, индивидуальными наклонностями и
интересами;
• расширение возможностей социализации учащихся, обеспечение
преемственности между общим и профессиональным образованием, более эффективная
подготовка выпускников школы к освоению программ высшего профессионального
образования.
Таким образом, необходимость создания практико-ориентированного образования вызвана стремлением общества обеспечить повышение качества жизни ныне живущих и будущих поколений людей на основе комплексного решения социальных, образовательных, экономических проблем.
В связи с этим разработчики ОГЭ и ЕГЭ предлагают учащимся перечень задач практико-ориентированного направления (В12 в ЕГЭ и во второй части ОГЭ).
В нашем лицее математики используют комплект учебников под редакцией Макарычева Ю. Н. для углубленного изучения математики 7- 9 классов и Мордковича А. Г. для профильного обучения в 10-11 классах, в которых рассматриваются задачи разнообразной тематики и уровня сложности, предлагаемых на экзаменах 9, 11 классов.
К ним относятся:
1. Задачи на движение:
· Задачи на движение по прямой (навстречу и вдогонку);
· Задачи на движение по замкнутой трассе;
· Задачи на движение по воде;
· Задачи на среднюю скорость;
· Задачи на движение протяженных тел;
2. Задачи производительность;
3. Задачи на арифметическую и геометрическую прогрессии;
4. Задачи на концентрацию, смеси и сплавы;
5. Задачи на проценты, части и доли;
6. Задачи на бассейны и трубы.
Ценность задач состоит в демонстрации их общности с точки зрения исследования и анализа реальных процессов средствами математики.
Решение задач состоит в построении математической модели по текстовому описанию конкретной ситуации и в применении этой модели для отыскания одной или нескольких величин, имеющих конкретный содержательный смысл. Как правило, математическая модель имеет форму алгебраического уравнения или системы уравнений, которая строится на основе содержательной интерпретации понятий и условий, характеризующих ситуацию в тексте задачи. Решение построенной модели обычно требует учета содержательного смысла используемых величин. Наконец, самому полученному решению модели должна быть дана содержательная интерпретация.
Учащиеся, как правило, испытывают трудности при решении задач, так как их систематическое решение заканчивается вместе с изучением курса математики 9-го класса. В курсе математики текстовые задачи представлены периодически, и они систематизированы по видам составляемых уравнений, а не по содержательной интерпретации. Кроме того, математическая формализация условий конкретных ситуаций предусматривает использование понятий и закономерностей, либо изучаемых вне математики, либо вытекающих из опыта практической жизни или здравого смысла.
Конечно, все задачи рассмотреть можно, но долго, поэтому мы остановимся на рассмотрении некоторых задач на движение, концентрацию, смеси, сплавы и сложный процент.
· Задачи на движение по прямой (навстречу и вдогонку):
При решении таких задач удобно считать одно тело неподвижным, а другое – приближающимся к нему со скоростью, равной сумме скоростей этих тел ( при движении навстречу) или разности скоростей (при движении вдогонку). Такая модель помогает разобраться с условием задачи, получить нужные уравнения.
Формулы, используемые для данных задач:
![]()
![]()
· Задачи на движение по замкнутой трассе:
При решении таких задач рассмотрим два условия:
Движение двух точек по
окружности длины s в
одном направлении при одновременном старте со скоростями v1
и v2, причем v1
> v2, то ответим на вопрос:
через какое время первая точка будет опережать вторую ровно на один круг?
Считая, что вторая точка покоится, а первая приближается к ней со скоростью v1
- v2, получим, что условие задачи будет
выполнено, когда первая точка поравняется в первый раз со второй, при этом
первая точка пройдет расстояние, равное длине одного круга, и искомая формула ![]()
А если две точки одновременно начинают движение по окружности в одну сторону со скоростями v1 и v2, причем v1 > v2, то первая точка приближается ко второй со скоростью v1 - v2 и в момент, когда первая точка в первый раз догоняет вторую, она проходит расстояние на один круг больше.
Задача из открытого банка данных ЕГЭ:
Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Решение:
Пусть
скорость велосипедиста х (м/мин), а мотоциклиста – у (м/мин), тогда за 10+30=40
минут велосипедист проедет 40х метров. ![]() (первая
встреча). А еще через 30 минут мотоциклист догнал велосипедиста во второй раз
(первая
встреча). А еще через 30 минут мотоциклист догнал велосипедиста во второй раз ![]() Решая систему уравнений, получаем,
что скорость мотоциклиста равна 80 (км/ч).
Решая систему уравнений, получаем,
что скорость мотоциклиста равна 80 (км/ч).
Ответ: 80.
· Задачи на среднюю скорость:
При решении таких задач
необходимо вспомнить из физики, что средняя скорость равна отношению пути,
пройденному телом к времени, за которое этот путь пройден. Если путь состоит из
нескольких участков, то следует вычислить всю длину пути и все время движения и
воспользоваться формулой ![]() .
.
Задача из открытого банка данных ЕГЭ:
Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение:
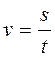 . S
=
190+180+170=540 (км). T =
190/50+180/90+170/100=7,5(ч).
. S
=
190+180+170=540 (км). T =
190/50+180/90+170/100=7,5(ч).
V = 540/7,5 = 72(км/ч).
Ответ: 72.
· Задачи на движение протяженных тел:
При решении таких задач требуется определить длину одного из них. Наиболее типичная ситуация: определение длины поезда, проезжающего мимо столба или протяженной платформы. В первом случае поезд проходит мимо столба – расстояние, равное длине поезда, во втором случае – расстояние, равное сумме длин поезда и платформы.
Задача из открытого банка данных ЕГЭ:
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй — длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение:
Будем считать, что первый сухогруз неподвижен, а второй приближается к нему со скоростью х(м/мин), равной разности скоростей второго и первого сухогрузов. Тогда за 12 минут второй сухогруз проходит расстояние
L=400+80+120+600=1200 (м). Поэтому х=1200/12=100 (м/мин), то есть 6 (км/час).
![]() Ответ:
6.
Ответ:
6.
Задачи на концентрацию, смеси и сплавы.
Решение этих задач традиционно является слабым звеном в подготовке школьников к сдаче экзаменов. Ключевой идеей при решении таких задач является отслеживание изменений, происходящих с «чистым» веществом.
Формула концентрации:
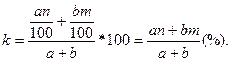 Где a,
b – количество литров в двух
растворах, а n и m
– процентное содержание водного раствора, к – концентрация получившейся смеси.
Где a,
b – количество литров в двух
растворах, а n и m
– процентное содержание водного раствора, к – концентрация получившейся смеси.
Рассмотрим задачу:
Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решение:
Используя формулу
концентрации получившегося раствора, 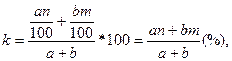 получим
получим 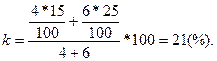
Ответ: 21.
А теперь рассмотрим решение задачи с помощью метода «стаканов».
Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Решение:
Х 30% У 60% 10 0% Х+у+10 36%
+ + =
Х 30% У 60% 10 50% Х+у+10 41%
+ + =
Составим систему уравнений:
![]() 30х+60у+10*0=(х+у+10)*36,
30х+60у+10*0=(х+у+10)*36,
30х+60у+10*50=(х+у+10)*41.
Решая ее, получаем х=60, у=30.
Ответ: 60.
Задачи на сложный процент:
При решении таких задач можно использовать следующую формулу:
![]() ,
где В – конечная величина, А – начальная величина,
,
где В – конечная величина, А – начальная величина, ![]() -
процент изменения ( в десятичной дроби), n
–
количество периодов, «+» - повышение, «-» - снижение.
-
процент изменения ( в десятичной дроби), n
–
количество периодов, «+» - повышение, «-» - снижение.
Рассмотрим следующую задачу:
Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20000 рублей, через два года был продан за 15842 рублей.
Решение:
В=15842 руб, А= 20000 руб, n=2.
Воспользуемся формулой ![]() , получим:
, получим:
![]() .
. ![]() =
11(%).
=
11(%).
Ответ: 11.
Рассмотрев данные задачи, можно сделать следующие выводы:
· Учебники дают возможность решать подобные задачи и подготовиться к сдаче ОГЭ и ЕГЭ;
· Учителям необходимо прививать интерес к решению текстовых задач;
· Необходимо учащимся знать эти формулы наизусть;
· Учителям обязательно проводить элективный курс по решению задач.
·
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.