Глава 9.        Решение вычислительных задач на компьютере

Практические работы

Практическая работа № 61.           
Решение уравнений методом перебора

Напишите программу, которая находит все решения заданного вам уравнения на интервале [-5;5].  Программа должна выполнить следующие действия:

1.       Определяет и выводит на экран интервалы, на которых расположены корни уравнения.

2.       На каждом интервале, используя метод перебора, ищет решение с точностью 0,001 и выводит полученные решения на экран.

Вычисление функции, стоящей в левой части уравнения, оформите в виде подпрограммы.

Уровень A. Интервалы, на которых расположены корни, можно найти с помощью электронных таблиц. Программа запрашивает левую границу очередного интервала и выводит найденный корень уравнения.

Пример:

Введите левую границу интервала:

1.5

Решение: 1.7201

Уровень B. Составить две программы, одна из которых выделяет все интервалы, на которых находятся корни, а вторая запрашивает левую границу очередного интервала и выводит найденный корень уравнения.

Уровень C. Составить одну программу, которая работает полностью автоматически: достаточно ввести в программу функцию и запустить. Программа находит все интервалы, на которых расположены корни и уточняет решения. После того, как очередной интервал найден, программа выводит его на экран и, применяя метод перебора с нужным шагом, уточняет решение.

Пример:

Интервал [-2;-1,5]

  Решение: -1.7201

Интервал [1,5;2]

  Решение: 1.7201

Варианты заданий по теме «Решение уравнений»

Практическая работа № 62.           
Решение уравнений методом деления отрезка пополам

Напишите программу, которая находит все решения заданного вам уравнения на интервале [-5;5].  Программа должна выполнить следующие действия:

1.       Определяет и выводит на экран интервалы, на которых расположены корни уравнения.

2.       Используя метод деления отрезка пополам, на каждом интервале ищет решение с точностью 0,001 и выводит полученные решения на экран.

Вычисление функции, стоящей в левой части уравнения, оформите в виде подпрограммы.

Уровень A. Интервалы, на которых расположены корни, можно найти с помощью электронных таблиц. Программа запрашивает границы очередного интервала и выводит найденный корень уравнения.

Пример:

Введите границы интервала:

1.5 2

Решение: 1.7201

Уровень B. Составить две программы, одна из которых выделяет все интервалы, на которых находятся корни, а вторая запрашивает границы очередного интервала и выводит найденный корень уравнения, а также число шагов, которые потребовались для достижения заданной точности.

Пример:

Введите границы интервала:

1.5 2

Решение: 1.7201

Число шагов: 8

Уровень C. Составить одну программу, которая работает полностью автоматически: достаточно ввести в программу функцию и запустить. Программа находит все интервалы, на которых расположены корни и уточняет решения. После того, как очередной интервал найден, программа выводит его на экран и, применяя метод деления отрезка пополам, уточняет решение и определяет необходимое для этого количество шагов.

Пример:

Интервал [-2;-1,5]

  Решение: -1.7201

  Число шагов: 8

Интервал [1,5;2]

  Решение: 1.7201

  Число шагов: 8

Практическая работа № 63.           
Решение уравнений в табличных процессорах

Уровень A. С помощью табличного процессора найдите все решения уравнения из примера «Полёт мяча», разобранного в учебнике.

Уровень B. Выполните задание уровня А. Затем выделите отдельную ячейку, в которой вычисляется максимальное значение функции  на выбранном интервале. Используя эту ячейку и подбор параметра, найдите:

1)      минимальную начальную скорость, при которой еще можно попасть в мишень;

2)      максимальное расстояние, при котором можно попасть в мишень при начальной скорости 15 м/с.

Уровень C. Выполните задание уровня B. Затем, используя замену , постройте аналитическое решение уравнения из примера «Полёт мяча». Для практических вычислений используйте электронные таблицы. Сравните точное и численное решения.

Практическая работа № 64.           
Вычисление длины кривой

Уровень A. Найдите длину параболы  на интервале .

Уровень B. Для примера «Полет мяча» вычислите длину траектории движения шарика для углов вылета 35,5° и 65,8°. Сравните полученные результаты.

Уровень C. Постройте с помощью табличного процессора эллипс, который описывается уравнением  при  и .  Напишите программу, которая вычисляет периметр этого эллипса с помощью дискретизации. Сравните ваш результат с тем, что получается по приближенной формуле Рамануджана: .

Экспериментально определите наибольший интервал дискретизации, при котором ошибка численного метода (в сравнении с результатом, полученным по формуле Рамануджана) составляет не более 1%.

Практическая работа № 65.           
Вычисление площади фигуры

Уровень A. Найдите площадь фигуры, ограниченной параболой  и осью OX, на интервале .

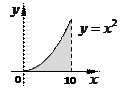
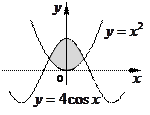
Уровень B. Найдите площадь фигуры, ограниченной графиками функций  и  .

Уровень C. Найдите площадь фигуры, ограниченной эллипсом

 при  и .

Сравните ваш результат с точным значением . Экспериментально определите наибольший интервал дискретизации, при котором ошибка численного метода составляет не более 1%.

Практическая работа № 66.           
Оптимизация. Метод дихотомии

Уровень A. Напишите программу, которая находит все минимумы и максимумы функции (см. варианты на следующей странице) на интервале [-5;5] с точностью 0,001, используя метод «золотого сечения». Границы интервала для поиска каждого минимума и максимума задаются вручную.

Уровень B. Напишите программу, которая находит все минимумы и максимумы функции (см. варианты на следующей странице) на интервале [-5;5] с точностью 0,001, используя метод «золотого сечения». Границы интервала для поиска каждого минимума и максимума определяются автоматически.

Уровень C. Напишите программу, которая находит все минимумы и максимумы функции (см. варианты на следующей странице) на интервале [-5;5] с точностью 0,001, используя метод «золотого сечения», причём на каждом шаге цикла вычисляется только одно новое значение функции. Границы интервала для поиска каждого минимума и максимума определяются автоматически.

Варианты заданий по теме «Оптимизация. Метод дихотомии»

Практическая работа № 67.           
Оптимизация с помощью табличных процессоров

Уровень A. В углах квадратного листа железа, сторона которого равна 1 м, вырезают четыре квадрата со стороной x. Затем складывают получившуюся развертку (по штриховым линиям на рисунке), сваривают швы и таким образом получается бак:

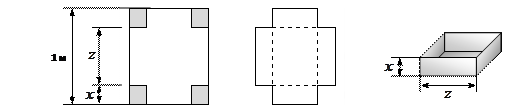
Определите размер выреза x, при котором получится бак наибольшего объема.

Уровень B. Выполните задание уровня А. Затем решите следующую задачу.

Фирма «Рога и копыта» хочет провести рекламную кампанию в газетах. Данные о цене рекламного объявления и тиражах газет внесены в таблицу:

В каждую газету нужно дать не менее одного и не более 6 объявлений. С помощью надстройки «Поиск решения» табличного процессора определите, сколько объявлений нужно дать в каждую газету, чтобы обеспечить общий охват не менее 200000 человек и при этом израсходовать как можно меньше денег.

Уровень C. Выполните задание уровня B. Затем решите следующую задачу[1].

Банка имеет форму цилиндра, размеры которого задаются радиусом  и высотой . Площадь полной поверхности банки вычисляется как сумма площади боковой поверхности и площадей двух кругов-оснований. Решите следующие задачи:

1)      найдите размеры банки, которая имеет максимальный объем при площади полной поверхности 100 см²;

2)      найдите размеры банки, которая имеет минимальную площадь полной поверхности при объеме 500 см³.

Практическая работа № 68.           
Статистические расчеты

В файле marks.xls вы найдете таблицу с оценками учеников по четырем предметам. Часть ее показана на рисунке:

1.    С помощью табличного процессора определите:

·      сколько пятерок, четверок и троек получено по каждому предмету;

·      среднюю оценку по каждому предмету;

·      средний балл каждого ученика

·      стандартное отклонение оценок по каждому предмету от среднего значения.

2.    Отсортируйте список учеников по убыванию среднего балла.

3.    Найдите коэффициенты корреляции (взаимосвязь) между оценками по разным предметам, а также между средним баллом и оценками по каждому из предметов. Оформите данные в виде таблицы:

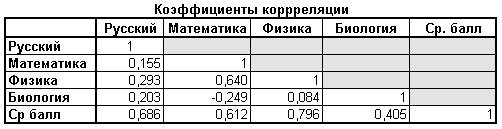
Оставьте у всех значений только три знака в дробной части.

Практическая работа № 69.           
Условные вычисления

Уровень A. В файле salary.xls вы найдете таблицу расчета зарплаты работников фирмы «Рога и Копыта». Требуется добавить нужные формулы в столбцах Премия и Сумма.

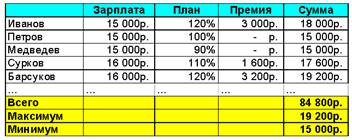
Работник получает премию пропорционально перевыполнению плана. Например, если план выполнен на 120% (перевыполнение на 20%), размер премии составит 20% от его зарплаты. Работник, сделавший меньше нормы, не получает премии.

Уровень B. В файле olimp.xls вы найдете таблицу результатов районной олимпиады по математике. На городской тур проходят те учащиеся, которые набрали на районном туре не менее 10 баллов или решили полностью одну из самых сложных задач 6 или 7. За полное решение задач 1-4 дается 2 балла, задач 5-6 – 3 балла, задачи 7 – 4 балла.

1) Добавьте необходимые формулы в столбцы Сумма и Прошел. Нужно сделать так, чтобы проходной балл можно было легко менять в отдельной ячейке.

2) Определите, сколько участников прошли на городскую олимпиаду.

3) Постройте график, который показывает, как изменяется количество прошедших на городскую олимпиаду при изменении проходного балла.

Уровень C. Выполните работу уровня B. После этого выполните дополнительное задание:

4) *Было принято решение предоставить льготы девушкам: сделать для них проходной балл на 1 меньше, чем для юношей. Внесите размер этой льготы в отдельную ячейку и определите число прошедших на городскую олимпиаду с учетом льготы.

Практическая работа № 70.           
Метод наименьших квадратов

Уровень A. 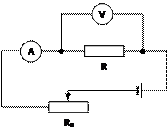Для того, чтобы определить неизвестное сопротивление резистора R собрали электрическую схему, показанную на рисунке. Напряжение на резисторе регулируется с помощью реостата R­₀ и измеряется вольтметром V. Сила тока в цепи измеряется амперметром A.

Задание:

В текстовом файле mnk.txt результаты измерений записаны в два столбца: в первом столбце напряжение на проводнике, а во втором – соответствующая ему сила тока. Всего в файле 10 строчек с данными.

1)      Напишите программу, которая читает данные из файла и вычисляет сопротивление резистора R, используя метод наименьших квадратов для закона Ома: .

2)      Решите ту же задачу с помощью табличного процессора. Сравните результаты.

Уровень B. Выполните задание уровня А при условии, что точное количество измерений (количество строк с данными в файле) неизвестно, но не больше 100.

После этого решите задачу, решив задачу оптимизации в табличном процессоре. Для вычисления величины ошибки используйте функцию SUMXMY2 (СУММКВРАЗН). Сравните полученные результаты.

Уровень C. Выполните задание уровня B. Затем с помощью табличного процессора решите задачу двумя другими методами:

Метод 2. Используйте в качестве критерия оптимизации не сумму квадратов отклонений, а сумму абсолютных величин (модулей) этих отклонений. Для вычисления модуля примените стандартную функцию ABS.

Метод 3. Закон Ома можно записать в виде , где . Используя метод наименьших квадратов, найдите оптимальное значение  с помощью своей программы и с помощью табличного процессора, а затем вычислите соответствующее значение .

Сравните результаты, полученные тремя методами. Какой из них вы рекомендуете использовать и почему?

Практическая работа № 71.           
Линии тренда

Уровень A.  Доходы начинающей фирмы (в тысячах рублей) за первые 5 лет работы приведены в таблице:

С помощью табличного процессора определите возможную зависимость дохода от года работы (выберите лучший из стандартных вариантов, с наибольшим значением ). С помощью этой зависимости сделайте прогноз развития фирмы на 2 года вперед.

Уровень B. По приведенным данным постройте три диаграммы типа «График», отображающую изменение прибыли каждой фирмы за несколько лет.

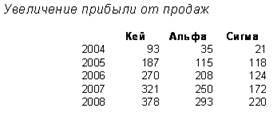
Определите заголовки осей и всей диаграммы.

Задание:

1)      Для каждого графика постройте линии тренда (нужно выбрать тип зависимости, который лучше всего соответствует данным).

2)      Выведите на каждую диаграмм формулу для линий тренда и величину достоверности аппроксимации R².

3)      Используя линии тренда, постройте графики прогнозируемых значений прибыли для всех фирм на следующие 5 лет. Подберите такой вид зависимости, который приводит к достоверным результатам прогноза.

4)      Используя уравнение линий тренда, вычислите прогнозируемые значения прибыли каждой фирмы на следующие пять лет.

Уровень C. В файле weather.xls в таблице записаны метеорологические данные: давление в миллиметрах ртутного столба и температура за первую половину месяца.

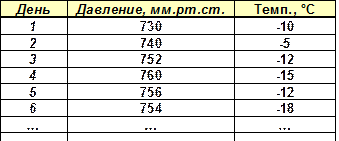
Предполагается, что изменение давления можно описать зависимостью вида

а изменение температуры — более сложной формулой

где  – номер дня.

Задание:

1)      Определите все неизвестные коэффициенты, при которых указанные формулы дают наиболее точное приближение к исходным данным.

2)      Оцените точность подбора зависимости, вычислив коэффициент R².

3)      Постройте графики, отображающие исходные данные и полученные функции (отдельно для давления и температуры). Сделайте прогноз изменения давления и температуры до конца месяца.

4)      Рассчитайте коэффициент корреляции исходных рядов давления и температуры. Какие выводы он позволяет сделать?

Скачано с www.znanio.ru