Решение задач на тему соотношение между сторонами и углами в прямоугольном треугольнике

Тема урока:  Соотношения между сторонами и углами прямоугольного треугольника.

Цели урока:
Образовательная: – совершенствовать навыки решения задач на применение теории подобных треугольников.
Развивающая: – развивать умения устанавливать причинно-следственную связь; строить логические рассуждения, умозаключения и выводы; умение работать с геометрическим текстом.
Воспитательная: – формирование ответственного отношения к учению, формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, умения находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме.

Ход урока.

      I.            Организационный момент. Мотивация учебной деятельности.

   II.            Актуализация знаний учащихся.

1. Решение задач по готовым чертежам.

III.            Решение задач.

Решить задачу № 576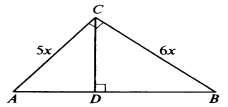               

            Решение: Пусть Х — коэффициент пропорциональность, тогда  АС = 5х, ВС = 6х.

Из ΔАСD  ( D = 90⁰) по теореме Пифагора АD² = АС² — СD² = 25х² — СD².

Из ΔВСD  (D = 90⁰) по теореме Пифагора ВD² = СВ² — СD² = 36х² — СD²

            ВD² — АD² = (36х² — СD²) — (25х² — СD²) = 11х²

            ВD² — АD² = (ВD — АD)(ВD + АD) = 11АВ, так как ВD на 11 см больше АD,
 ВD + АD = АВ.

Следовательно 11х² = 11АВ, отсюда  АВ = х²

Из ΔАВС  (С = 90⁰) по теореме Пифагора АВ² = АС² + ВС² = 25х² + 36х² = 61х², отсюда  АВ = х;  х² = х ;  х =  ;   АВ = 61 см.

IV.            Самостоятельная работа.

Вариант—1

               Найти: СН, АС, ВС  S_АСН : S_ВСН.

2. Высота, проведенная из вершины прямого угла прямоугольного треугольника, равна 6 см и делит гипотенузу на отрезки, один из которых больше другого на 5 см. Найдите стороны треугольника. В каком отношении данная высота делит площадь треугольника?

Вариант—2

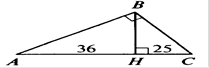                   Найти:  ВН, АВ, ВС,   S_АВН : S_ВСН .

2. В прямоугольном треугольнике АВС (С=90⁰) проведена высота СD так, что длина отрезка ВD на 4 см больше длины отрезка СD, АD = 9 см. Найдите стороны треугольника АВС. В каком отношении СD делит площадь треугольника АВС?

Дополнительная задача:

Биссектриса острого угла СDА трапеции АВСD пересекает сторону АВ в точке К. Из точки К проведен перпендикуляр КЕ к стороне СD так, что СЕ = 9 см, DЕ = 16 см. Найдите КЕ и стороны трапеции, если угол А = 90⁰, К — середина АВ.

Ответ:   КЕ = 12 см, АВ = 24 см, ВС = 9 см, СD = 25 см, АD = 16 см.

    V.            Рефлексия учебной деятельности.

1. Что называют средним геометрическим (средним пропорциональным) двух отрезков?

2. Сформулируйте свойство высоты прямоугольного треугольника, проведенной из вершины прямого угла.

3. Сформулируйте утверждение о пропорциональных отрезках в прямоугольном треугольнике.

Домашнее задание:     гл.7, п.65 стр.146, вопр. 10, 11 (стр.158)
                                      решить зад. №575, 577, 579.