Решение задач по теме «Параллельность прямой и плоскости».

Урок 9. Решение задач по теме «Параллельность прямой и плоскости».

Цели урока: обобщить изученный материал; закрепить навыки применения изученных теорем к решению задач; воспитывать самостоятельность в выборе способа решения геометрических задач.

Ход урока.

I. Организационный момент.                                                                                                               Сообщить тему и цели урока.

II. Проверка домашнего задания.                                                                                                           Проверить задачи № 24, 31, комментируя решение.

III. Актуализация знаний учащихся.

1) Фронтальный опрос.                                                                                                                                    - Сформулируйте теорему о трех параллельных прямых.                                                                                      - Сформулируйте признак параллельности прямой и плоскости.                                                                                  - Верно ли утверждение, что если прямая, не лежащая в плоскости, параллельна ей, то она параллельна любой прямой, лежащей в этой плоскости? (Нет.)                                                                                   - Верно ли утверждение, что если две прямые параллельны одной и той же плоскости, то они параллельны между собой? (Нет.)                                                                                                                          - Каким может быть взаимное расположение двух прямых, из которых одна параллельна некоторой плоскости, а другая пересекает эту плоскость?

2) Индивидуальная работа по карточкам (3 ученика).                                                                                                               С остальными учениками решение задач № 29, 30.

I уровень

Карточка 3

Через основание AD трапеции ABCD проведена плоскость α. ВС ∉ α. Докажите, что прямая, проходящая через середины сторон АВ и CD, параллельна плоскости α.

Дано: ABCD - трапеция; AD ∈ α, СВ ∉ α; АК = КВ, CN = ND (рис. 3).

Доказать: KN || α.

 

 

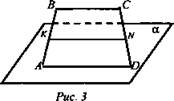
Доказательство:

1. KN - средняя линия трапеции, значит KN || AD.

2.  (по теореме о параллельности прямой и плоскости).

 

II уровень

Карточка 2

Дан ΔВСЕ. Плоскость, параллельная прямой СЕ, пересекает BE в точке Е1, а ВС - в точке С1. Найдите ВС1, если С1Е1 : СЕ = 3 : 8, ВС = 28 см.

Дано:  (рис. 2).

Найти: ВС1.

 

 

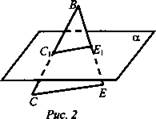
Решение:

1.

2. ΔВС1Е1 ~ ΔВСЕ (по двум углам);  (Ответ: 10,5 см.)

 

III уровень

Карточка 1

№ 1. Доказать, что если через каждую их двух параллельных прямых проведена плоскость, причем эти плоскости пересекаются, то линия их пересечения параллельна каждой из данных прямых.

Дано:   (рис. 1).

Доказать: а || с, b || с.

 

 

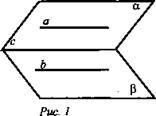
Доказательство:

1.  по признаку.

2.

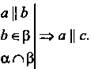
3. Аналогично b || с.

 

№ 29. Дано: ABCD - трапеция, ВС = 12 см, M ∈ (ABC), ВК = КМ (рис. 4).

Доказать: (ADK) ∩ МС = Н.

Найти: КН.

 

 

Решение:

1.

2.

3.

4.  следовательно КН - средняя линия ΔВМС. КН = 6 см.

№ 30. Дано: ABCD - трапеция, АВ || α, С ∈ α (рис. 5).

Доказать: CD ∩ ∈; MN || ∈, где MN - средняя линия трапеции.

 

 

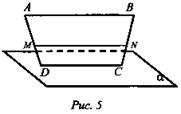
Доказательство:

1. Пусть CD ∉ α, тогда CD ∩ α = С,

 по лемме АВ ∩ α. Но АВ || α — это противоречие, значит, CD ∈ α.

2.  (по признаку).

 

V. Самостоятельная работа обучающего характера (с оказанием индивидуальной дифференцируемой помощи) (см. приложение)

 

 

 

 

Ответы и указания к задачам самостоятельной работы.

I уровень

Вариант I

1.  - средняя линия.

 (Ответ: 4 см.)

КМ || EF (теорема о параллельности трех прямых).

2. Дано: ABCD - трапеция; AD ∈ α, АЕ = ЕВ, CF = FD (рис. 8).

Доказать: EF || α.

 

 

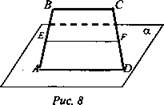
Доказательство: Так как АЕ = ЕВ, CF = FD, значит, EF - средняя линия трапеции ABCD.

 (по теореме о параллельности прямой и плоскости)

 

Вариант II

1. Решение:

 - средняя линия трапеции

2) ABCD - квадрат, АВ = ВС = CD = DA, АВ || CD, AD || ВС.

 (Ответ: 8 см.)

2. Дано: ΔABC, AC ∈ α, AD = DB, BE = EC (рис. 9).

Доказать: DE || α.

 

 

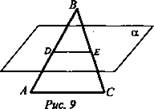
Доказательство:

1) Так как  - средняя линия ΔАВС.

2)  (по признаку).

 

II уровень

Вариант I

1. Дано: А, В, С, D; В ∉ (ACD). Е, F, М, К- середины сторон АВ, ВС, CD, AD; AC = 6 см, BD = 8 см (рис. 10).

Доказать: EFMK - параллелограмм.

Найти: PEFMK.

 

 

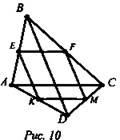
Решение:

1)  - средняя линия,

2)  - средняя линия, МК || АС, КМ = 1/2АС. EF || AC (значит EF || (ACD)), АС || КМ ⇒ EF || КМ по теореме о параллельности прямой и плоскости.

3) Аналогично ЕК || FM.

4) EFMK - параллелограмм, то есть EF || КМ, ЕК || FM.

5) Учитывая свойства параллелограмма

6) Из п. 1 и 2 следует, что

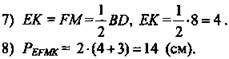 (Ответ: 14 см.)

 

 

2. Дано:   (рис. 11).

Доказать: b ∈ α.

 

 

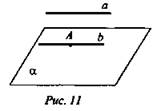
Доказательство:

 значит, b || α, но учитывая, что

 

Вариант II

1. Дано: А ∉ (BCD); AR = RD, АР = РВ, ВТ = ТС, DS = SC; BD = 6 см, PPRST = 14 см (рис. 12).

Доказать: PRST - параллелограмм.

Найти: АС.

 

 

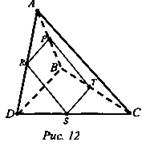
Решение:

1)  - средняя линия,

 - средняя линия,

 - средняя линия,  Из б и в следует, что РТ || RS (по теореме о параллельности трех прямых).

 - средняя линия,  Из а и д следует, что TS || RP (по теореме о параллельности трех прямых). TS = RP.

2)  (Ответ: 8 см.)

2. Дано: a || b, В ∈ b, В ∈ α, a || α (рис. 13).

Доказать: b ∈ α.

 

 

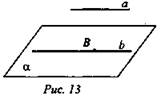
Доказательство:

1) Допустим, b ∉ α, b ∩ α = В, по признаку, если  что противоречит условию. Значит, b || α, но так как

 

 

III уровень

Вариант I

1. Дано: ΔАВК, М ∉ (АВК); E.D- точки пересечения медиан ΔМВК и ΔАВМ; АК = 14 см (рис. 14).

Доказать: ADEK - трапеция.

Найти: DE.

 

 

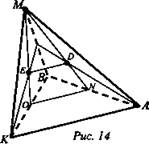
Решение:

1)  - средняя линия ON || AK, ON = 1/2AK.

2) Рассмотрим (MNO). ΔMON ∈ (MNO). Точки Е и     D - точки пересечения медиан: по свойству медиан

3) ΔMED ~ ΔMON ∠M - общий  значит, ∠MED = ∠МОN, то есть ED || ON.

4)  (по теореме о параллельности прямой и плоскости).

5) Из п. 1,3   по признаку, значит, KEDA – трапеция, ED и AK - основания.

6)  (из п. 1),

7) Рассмотрим ΔMED и ΔMON, ΔMED ~ ΔMON (из п. 3), значит,  (Ответ: )

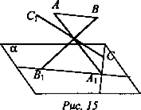
2. Дано: АА1, BB1, СС1; О - середина отрезков (рис. 15).

Доказать: АВ || (А1С1В1).

 

 

Доказательство:

1) Так как AA1 ∩ BB1 = 0, существует α = (АВА1В1), α - единственна.

2) АО = OA1, ВО = ОВ1, значит, АВА1В1 - параллелограмм, по свойству параллелограмма АВ || A1B1, AB1 || А1В.

3) А1В1 ∈ (A1В1C), АВ ∉ (А1В1С) по теореме о параллельности прямой и плоскости.

 

 

Вариант II

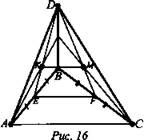
1. Дано: А, В, С, D; D ∉ (ABC), К, М - точки пересечения медиан треугольников, ΔАBD и ΔBCD, КМ = 6 см (рис. 16).

Доказать: КМ || АС.

Найти: АС.

 

 

Решение:

1)  - средняя линия

2) Рассмотрим (EDF): ΔEDF ∈ (EDF), ΔKDM ~ ΔEDF, ∠D - общий,  (по свойству медиан треугольника ).

3) Из ΔKDM ~ ΔEDF ⇒ ∠DKM = ∠DEF, значит, КМ || EF.

4) 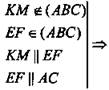 KM || АС по теореме о параллельности прямой и плоскости.

Из п. 1  (Ответ: 18 см.)

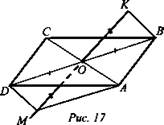
2. Дано: ABCD - параллелограмм. О - точка пересечения диагоналей АС и BD; (КМ) ∩ (ABCD) = О; КО = ОМ (рис. 17).

Доказать: КВ || (AMD).

 

 

Доказательство:

1) Существует (KBMD), так как КМ ∩ BD плоскость (KBMD) - единственная.

2) BKDM: ВО = OD, КО = ОМ, значит BKDM - параллелограмм, то есть по свойству параллелограмма КВ || DM.

3) 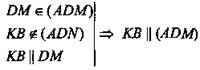   по теореме о параллельности прямой и плоскости.

 

VI. Подведение итогов урока.

 

 

VII. Домашнее задание:

I уровень: № 23, № 25.

II уровень: № 23, 25, дополнительная задача № 88.

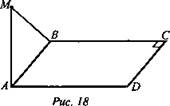
№ 23. Дано: ABCD - прямоугольник; M ∉ (ABCD) (рис. 18).

Доказать: CD || (АВМ).

 

 

Доказательство:

С ∉ (ABM), D ∉ (АВМ), так как M ∉ (ABCD), значит, CD ∩ (АВМ) или CD || (АВМ) - по признаку.

№ 25. Дано:   (рис. 19).

 

 

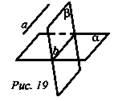
Доказать:

Доказательство:

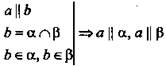 по признаку.

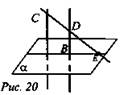
№ 88. Дано: AC || BD, AC ∩ α = A; BD ∩ α = B. AC = 8 cm, BD = 6 см, AB = 4 см (рис. 20).

Доказать: CD ∩ α = E.

Найти: BE.

 

 

Решение:

1) Проведем плоскость (ACDB), если CD || АВ, то ACDB - параллелограмм, то есть АС = BD, но это противоречит условию, значит, CD ∩ AB = Е.

2) Рассмотрим ΔАСЕ и ΔBDE.

∠CAE = ∠DBE, ∠АСЕ = ∠BDE - как соответственные при параллельных прямых, значит, ΔEDB ~ ΔЕСА (по 3 углам) следовательно,  то есть  BE = 12 (см). (Ответ: BE = 12 cm.)

 

 

Скачано с www.znanio.ru