Г.А. Клековкин

 

 

 

 

 

 

 

 

 

 

 

Решение геометрических задач векторным методом

 

 

Учебное пособие для учащихся 10-11 классов

 

 

 

 

 

 

 

 

Самара

2016

УДК 373.167.1:514

ББК 22.151.0, 74.202.63, 74.262.215

        К48

Печатается по решению Ученого совета СФ ГАОУ ВО МГПУ

 

Рецензенты:

Дорофеев С.Н., доктор педагогических наук, профессор кафедры алгебры и геометрии Тольяттинского государственного университета

Ястребов А.В., доктор педагогических наук, профессор кафедры математического анализа, теории и методики обучения математике

Ярославского государственного педагогического университета им. К.Д. Ушинского

 

Клековкин Г.А.

К48     Решение геометрических задач векторным методом: учебное пособие для учащихся 10-11 классов / Г.А. Клековкин. – Самара: СФ ГАОУ ВО МГПУ, 2016. – 180 с.

 

ISBN 

 

В пособии выделены опорные задачи и формулы, лежащие в основе векторного метода решения геометрических задач. Приводится большое количество примеров использования этих задач и формул. Особое внимание уделено одновременному решению планиметрических задач и их пространственных аналогов.

Пособие адресовано учащимся 10-11 классов с профильным и углубленным изучением математики. Учителя математики могут использовать его для разработки соответствующих элективных курсов, а преподаватели вузов – курсов по выбору для будущих учителей математики.

 

УДК 373. 167.1:514

ББК 22.151.0, 74.202.63, 74.262.215

 

© , 2016

ISBN                                                                 © Г.А. Клековкин, 2016

             

Содержание

 

                   Введение                                                                            5

                  Глава I. Векторы в школьном курсе геометрии

       § 1. Вектор. Равенство векторов                                                                     9

                   1.1.         Понятие вектора                                                                           9

                   1.2.         Равенство векторов                                                                   10

       § 2. Сложение векторов                                                                                    12

                   2.1.         Определение суммы векторов                                               12

                   2.2.         Свойства сложения векторов                                                 13

                   2.3.         Вычитание векторов                                                                 14

       § 3. Умножение вектора на число                                                                 15

                   3.1.         Определение произведения вектора на число                  15

                   3.2.         Свойства произведения вектора на число                          15

       § 4. Координаты вектора                                                                                 16

                   4.1.         Коллинеарные и компланарные векторы                           16

                   4.2.         Определение координат вектора                                           17

                   4.3.         Свойства координат вектора                                                  18

       § 5. Скалярное произведение векторов                                                     18

                   5.1.         Угол между векторами                                                            18

                   5.2.         Определение скалярного произведения векторов           19

                   5.3.         Свойства скалярного произведения векторов                   19

                            5.4.       Скалярное произведение векторов, заданных ко-  ординатами       20

       § 6. Взаимосвязи векторного и координатного методов                      21

                   6.1.         Краткая историческая справка                                              21

                   6.2.         Базис. Координаты вектора в базисе                                   24

                                  Задачи для повторения                                                             28

                Глава II. Аффинные задачи                                                

§ 2.1. Опорные аффинные задачи и формулы   31           2.1.2.      Принадлежность точки прямой (плоскости)           31

                   2.1.2.      Взаимное расположение двух прямых                                33

                   2.1.3.      Взаимное расположение прямой и плоскости                  34

                   2.1.4.     Взаимное расположение двух плоскостей                         34

                   2.1.5.      Деление отрезка в данном отношении                                35

                   2.1.6.      Отношение отрезков параллельных прямых                     39

§ 2.2. Применение опорных задач и формул       41           2.2.1.      Формула деления отрезка пополам            41

                            2.2.2.   Использование опорных задач и формулы деле-   44 ния отрезка в данном отношении

                                   Задачи для самостоятельного решения                               48

 

§ 2.3. Медианы треугольника и тетраэдра                                                51

            2.3.1.      Опорные задачи и формулы                                                   51

            2.3.2       Применение опорных задач и формул                                55

                            Задачи для самостоятельного решения                               57

§ 2.4. Теоремы инцидентности                                                                       58

            2.4.1.      Теоремы Менелая и Чевы и их стереометрические             

                            аналоги                                                                                         58

            2.4.2.      Применения опорных теорем                                                64

                            Задачи для самостоятельного решения                               75

            Глава III. Метрические задачи                                                               

§ 3.1. Задачи на доказательство и вычисление                                       79

            3.1.1.      Основные формулы и приемы                                              79

            3.1.2      Задачи на доказательство                                                        87

            3.1.3      Задачи на вычисление                                                              91

                            Задачи для самостоятельного решения                             109

§ 3.2. Двугранные и трехгранные углы                                                    112

            3.2.1.      Двугранный угол                                                                     112

            3.2.2       Трехгранный угол. Теоремы косинусов и синусов               

                            для трехгранного угла                                                           115

            3.2.3.      Трехгранный угол и сфера                                                   123

                            Задачи для самостоятельного решения                             132

§ 3.3. Замечательные точки треугольника и тетраэдра                     136

            3.3.1.      От треугольника к тетраэдру                                               136

            3.3.2.      Связь между замечательными точками треуголь-              

                            ника                                                                                             149

            3.3.3.     Ортоцентрический тетраэдр                                                 152

            3.3.4.      Равногранный тетраэдр                                                         158

                            Задачи для самостоятельного решения                             164

            Ответы, указания, решения                                                             170

            Литература                                                                                              178

 

 

             

ВВЕДЕНИЕ

 

Предлагаемое пособие адресовано старшеклассникам, которые собираются продолжить свое математическое образование в высшей школе. Его появление обусловлено тем, что уже более полувека специальные геометрические курсы в классических и педагогических университетах и геометрические разделы курсов высшей математики в технических и др. вузах строятся на векторной основе. Вектор является фундаментальным понятием курсов линейной алгебры, функционального анализа, линейного программирования и многих других математических дисциплин; без него невозможно представить современное изложение механики, теории относительности, теоретической физики.

В вузовских курсах вектор обычно вводится аксиоматически, как элемент векторного (линейного) пространства. Чтобы быть готовым к изучению этих курсов, важно еще в школе получить опыт использования векторов на функциональном уровне, т. е. научиться применять векторы при решении задач. Школьный курс геометрии открывает для этого широкие возможности. Во-первых, вектор почти во всех школьных учебниках определяется геометрически, как направленный отрезок. Это позволяет дать простые и наглядные интерпретации как самому понятию «вектор», так и операциям над векторами; что, как показывает практика, крайне важно при первом знакомстве с любым математическим понятием. Вовторых, имеется огромное число геометрических задач (теорем), которые с помощью векторов решаются (доказываются) более просто и красиво, чем другими методами. В пособии будут приведены примеры таких задач и теорем.

На уроках геометрии многие из вас заметили, что векторный метод решения геометрических задач тесно связан с методом координат. Геометрическую задачу, которую можно решить с помощью метода координат, можно решить векторным методом, и, наоборот, любое векторное решение задачи можно оформить в координатной форме.

Первое знакомство с системой координат на плоскости происходит еще на уроках математики в 5-6 классах. В курсе алгебры основной школы система координат на плоскости становится важнейшим средством изучения функций и их свойств, графического решения уравнений и неравенств; в курсе алгебры и начал анализа она, кроме того, незаменима при изучении производной, интеграла и их приложений. В этих курсах используется прямоугольная система координат  с равными единицами измерения длин на координатных осях  и . В таком же виде она появляется и в курсе планиметрии: координатные векторы ,  осей ортогональны и имеют единичную длину. При изучении стереометрии также применяется только прямоугольная система координат.

При решении геометрических задач методом координат к рассматриваемым в них геометрическим фигурам присоединяется система координат. Поэтому систему координат часто сравнивают с лесами, которые применяются при строительстве и ремонте зданий. И строительные леса, и система координат выполняют вспомогательные функции; они должны в некотором смысле обеспечивать оптимальные удобства тому, кто их использует.

Решая задачи методом координат, вы, наверняка, обратили внимание на то, что сложность аналитических вычислений может существенно зависеть от способа присоединения системы координат к исследуемой в задаче геометрической фигуре. Кроме того, часто приходится, рассматривать различные частные случаи, появление которых обусловлено расположением элементов фигуры относительно системы координат. Увидели вы и то, что громоздкость координатных решений стереометрических задач, как правило, выше, чем у аналогичных планиметрических. Наконец, нередко дополнительные трудности, которых можно избежать, обусловлены тем, что в школе при решении любых задач обычно применяются только прямоугольные системы координат, хотя интуитивно ясно, что для решения некоторых задач лучше бы «подошли» какие-то другие системы координат, «более тесно» связанные с изучаемыми в них фигурами. Такими системами являются, например, аффинные системы координат, которые в школе не рассматриваются. (Координатными векторами аффинной системы координат на плоскости служит любая упорядоченная пара неколлинеарных векторов, лежащих в плоскости или ей параллельных, а координатными векторами аффинной системы координат в пространстве

– любая упорядоченная тройка некопланарных векторов.)

Подчеркнем, что геометрические свойства фигуры не зависят от выбора системы координат, которая применяется для ее изучения. Поэтому при использовании метода координат геометрические свойства фигуры называют ее инвариантами. Дать пригодные для всех случаев рекомендации, как присоединить к изучаемой фигуре систему координат, чтобы в последующем минимизировать аналитические вычисления, не представляется возможным. Умение делать оптимальный выбор системы координат приходит с опытом.

Векторы при решении геометрических задач векторным методом также являются вспомогательными средствами, а их «прикрепление» к рассматриваемым фигурам может осуществляться разными способами. Чем тогда объяснить выбор этого метода в качестве предмета углубленного изучения? Векторный метод основан на использовании аппарата векторной алгебры, что обеспечивает его большую общность и универсальность. Векторные решения многих задач не зависят от того, является рассматриваемая фигура плоской или пространственной; в подобных случаях в решении используются одни и те же алгебраические выкладки. Для некоторых планиметрических задач и их стереометрических аналогов характерно то, что векторное решение плоскостной задачи естественным образом корректируется для соответствующей пространственной. Наконец, при использовании этого метода, как правило, отпадает необходимость рассматривать многочисленные частные случаи.

В заключение отметим некоторые методические особенности, которыми пособие может отличаться от учебника геометрии.

1.                   В школьных учебниках векторы изучаются в два приема: в основной школе рассматриваются двумерные векторы, в старшей школе – трехмерные. К сожалению, такой подход не всегда позволяет продемонстрировать истинную ценность векторного метода, которая, как было сказано, заключается в легкой трансформации известных решений на любые размерности. Поэтому в пособии большое внимание уделяется именно подобным трансформациям и аналогиям, а значит, нет привычного разделения и отдельного рассмотрения планиметрических и стереометрических задач.

2.                   Изучаемые в школе свойства геометрических фигур, а, значит, теоремы и задачи, можно разбить на аффинные и метрические.

Аффинными называются свойства фигур, которые сохраняются (остаются инвариантными) при параллельном проектировании. В их число входят: отношение трех точек прямой; принадлежность точек прямым и плоскостям; принадлежность прямой плоскости; параллельность прямых и плоскостей; отношение отрезков, лежащих на одной прямой или параллельных прямых; отношения площадей и объемов. Теоремы и задачи, в которых рассматриваются аффинные свойства фигур, также называют аффинными. Примерами аффинных теорем являются, например, теоремы о пересечении диагоналей параллелограмма и параллелепипеда, о пересечении медиан треугольника и т. д.

Длины отрезков, меры углов, площади и объемы геометрических фигур в общем случае не сохраняются при параллельном проектировании, но сохраняются при движениях. Свойства фигур, инвариантные при движениях и подобиях, называются метрическими. Теоремы и задачи, в которых рассматриваются метрические свойства фигур, называются метрическими. Примерами метрических утверждений служат: теорема Пифагора и теорема, обратная ей; теорема о пересечении прямых, содержащих высоты треугольника, признаки перпендикулярности прямой и плоскости (двух плоскостей) и т. п.

Программа школьного курса геометрии не предусматривает знакомство с понятиями «аффинная задача» и «метрическая задача». Однако с таким разделением задач вы почти обязательно столкнетесь в дополнительной литературе, посвященной координатному и векторному методу. При использовании этих методов такое разделение, как вы увидите на примере векторного метода, становится очевидным и целесообразным.

Поэтому вместо привычного деления задач на планиметрические и стереометрические в пособии на первый план выходит разбиение задач на аффинные и метрические.

3. В большинстве случаев ход решения математической задачи представляет собой решение некоторой последовательности подзадач, способы решения которых известны. Поэтому во множестве задач обычно пытаются выделить задачи, которые наиболее часто встречаются в процессе решения других задач. Такие задачи принято называть ключевыми или опорными.

При использовании геометрического и обычных алгебраических методов выделить опорные задачи и составить оптимальный список таких задач достаточно трудно. Поэтому списки опорных задач, предлагаемые авторами различных дополнительных руководств по решению школьных геометрических задач этими методами, нередко существенно отличаются друг от друга.

Координатный и векторный методы делают процедуру выделения опорных задач и формул естественной и прозрачной. При использовании векторного метода в число опорных аффинных задач войдут задачи, позволяющие с помощью векторов выражать перечисленные выше аффинные свойства основных геометрических фигур (точек, прямых и плоскостей). Для векторного описания этих свойств, как вы увидите, достаточно операций сложения и вычитания векторов и операции умножения вектора на число. В число опорных метрических задач войдут прежде всего задачи, в которых на векторной основе строятся алгоритмы вычисления длин, углов и других метрических величин. Для решения этих опорных задач и записи полученных при этом опорных формул кроме названных операций используется скалярное произведение векторов. (Следует заметить, что в вузовских курсах для изучения метрических свойств наряду со скалярным произведением вводятся операции векторного и смешанного умножения векторов. Поскольку в базовом школьном курсе геометрии эти операции не рассматриваются, то в пособии для вычисления всех метрических величин используется только скалярное произведение.)

Выделение опорных задач и формул позволяет сводить решение многих школьных геометрических задач к применению известных формул и стандартных приемов, ведущих от условия задачи к искомому результату, и тем самым алгоритмизировать процесс их решения.

Данное пособие будет полезно и тем выпускникам школы, которые просто хотят успешно сдать ЕГЭ по математике. В части 2 действующего сегодня формата экзамена содержится стереометрическая задача, которая часто легко решается с помощью координатного или векторного методов.

Кроме того, отдельные планиметрические задачи этой части также имеют простые и красивые векторные решения.  

Глава I

 

ВЕКТОРЫ В ШКОЛЬНОМ КУРСЕ ГЕОМЕТРИИ

 

В настоящее время в школе используется несколько различных учебников геометрии, в каждом из которых изложение темы «Векторы» имеет свои методические особенности. Цель данной главы – дать обзор основных понятий темы и условиться об используемых в пособии обозначениях и терминологии. Все теоремы и свойства понятий приводятся в главе без доказательств; в случае необходимости отсутствующие доказательства можно найти в любом из школьных учебников геометрии.

Прежде чем перейти к изучению основного материала пособия, рекомендуется решить задачи для повторения, которые приведены в конце главы.

 

§ 1. Вектор. Равенство векторов

 

1.1. Понятие вектора. В школьных учебно-методических комплектах по геометрии вектор определяется как направленный отрезок.

Направленный отрезок или вектор – это отрезок, у которого один из его концов считается первым и называется началом, а другой конец – вторым и называется концом. Направленный отрезок с началом  и концом  обозначают  и изображают в виде отрезка со стрелкой на конце .

Если записи ,  обозначают один и тот же обычный (ненаправленный) отрезок с концами  и , то записи ,  обозначают разные направленные отрезки. Для направленного отрезка  началом служит точка , а концом – точка . Поэтому направленные отрезки (векторы)  и  называют противоположными.

Векторы обозначают также строчными полужирными буквами латинского алфавита: , , , … или строчными буквами со стрелкой: , , , …

Длиной вектора  называют длину соответствующего ему отрезка , длину вектора  обозначают . Из этого определения следует, что .

Вектор, длина которого равна единице, называется единичным вектором или ортом.

Вектор, конец которого совпадает с его началом, т. е. точку, называют нулевым или нуль-вектором. Если точка, соответствующая нулевому вектору, обозначена буквой , то сам вектор обозначают . Длина нулевого вектора равна нулю: . Для обозначения нулевого вектора используют, кроме того, записи  и . Вектор :

–      лежит на прямой  (в плоскости ), если на прямой  (в плоскости ) лежит отрезок ;

–      параллелен прямой  (плоскости ), если прямой  (плоскости ) параллелен отрезок ;

–      перпендикулярен прямой  (плоскости ), если прямой  (плоскости ) перпендикулярен отрезок .

Два ненулевых вектора  и  называются одинаково направленными (сонаправленными), если сонаправлены лучи  и  (рис. 1.1). При этом пишут . Нулевой вектор считается сонаправленным с любым вектором. 

       a)                                                                             а)

                         C                                                                     D

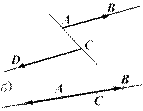                        Рис. 1.1                                                                       Рис. 1.2

Два ненулевых вектора  и  называются противоположно направленными, если противоположно направлены лучи  и  

(рис. 1.2). При этом пишут .

Всякий ненулевой вектор задает направление на прямой (на плоскости, в пространстве).

1.2. Равенство векторов. Два вектора называются равными, если они сонаправлены и имеют одну и ту же длину. Если вектор  равен вектору , то пишут . Таким образом,  тогда и только тогда, когда  и . В частности, все нулевые векторы равны между собой.

Отношение равенства векторов обладает свойствами:

1)  рефлексивности: ;

2)  симметричности: если

3)  транзитивности: если  и , то .

Имеет место теорема 1 (об откладывании вектора): для любого вектора  и любой точки  существует вектор , равный вектору , и притом только один.

                                ^A                                            Рис. 1.3

Из теоремы 1 вытекает, что равенство  имеет место тогда и только тогда, когда  (рис. 1.3).

На основании теоремы об откладывании вектора можно ввести понятие свободного вектора, понимая под ним множество всех равных между собой направленных отрезков. При этом каждый из равных между собой направленных отрезков считается представителем свободного вектора и однозначно его определяет. Иными словами, предложение «От точки  отложен свободный вектор » означает, что построен направленный отрезок , представляющий этот вектор; при этом пишут .

Параллельным переносом  пространства на вектор  называется ото-     ^M′

бражение пространства на себя, при котором произвольная точка  переходит в M

         такую точку , что  (рис. 1.4)                  Рис. 1.4

Аналогично определяется параллельный перенос плоскости (прямой), при этом требуется, чтобы вектор  был параллелен этой плоскости (прямой) или лежал в ней. Поэтому свободный вектор часто определяют как параллельный перенос пространства (плоскости, прямой). 

§ 2. Сложение векторов

 

2.1. Определение суммы векторов. Пусть даны два вектора  и ; их можно задать при помощи направленных отрезков, представляющих эти векторы. Сложение векторов определяется как последовательное выполнение двух параллельных переносов.

От произвольной точки  откладывается направленный отрезок

, равный вектору . Затем от конца  направленного отрезка  откладывается направленный отрезок , равный вектору

. В результате параллельного переноса, сначала на вектор , а затем на вектор , точка  перейдет в точку . Этот же результат можно получить в результате переноса точки  на вектор , представленный направленным отрезком  (рис. 1.5). Поэтому вектор  принимают за сумму векторов  и ; при этом пишут: . Для представителей складываемых векторов это равенство записывается так:

.                                  (1.1)

                                            _С                                                                       D

                       Рис. 1.5                                                         Рис. 1.6

В учебниках геометрии доказывается, что приведенное определение суммы векторов корректно, т. е. не зависит от выбора точки . Описанный способ определения и построения суммы двух векторов называется правилом треугольника.

Второй способ нахождения суммы двух векторов – правило параллелограмма – в физике связывают с нахождением равнодействующей двух сил, одновременно приложенных к некоторому телу (рис. 1.6). Его математическое обоснование опирается на следствие из теоремы 1 об откладывании вектора.

             

2.2. Свойства сложения векторов. Операция сложения векторов удовлетворяет следующим свойствам:

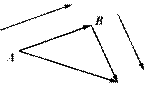
1.    Сложение векторов коммутативно, т. е.

                                      (1.2)

для любых векторов  и  (рис. 1.7).

                                        Рис. 1.7                                                     Рис. 1.8

2.    Сложение векторов ассоциативно^[1], т. е.

                           (1.3)

для любых векторов ,  и  (рис. 1.8).

3.    Нулевой вектор является нейтральным относительно операции сложения, т. е.

                                  (1.4)

для любого вектора . Для конкретных представителей эти равенства записывается так:

.

4.    Сумма противоположных векторов есть нуль-вектор, т. е.

 

или

.                                     (1.5)

На основании свойства 2 сумму  векторов , , …, ,   можно записывать опуская скобки и вычислять ее по правилу многоугольника:

.

В силу же свойства 1 в этой сумме можно произвольным образом менять порядок слагаемых.

 

 

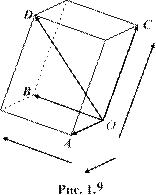
При вычислении суммы трех векторов ,  и , не параллельных одной плоскости, используется правило параллелепипеда, аналогичное правилу параллелограмма. Направленные отрезки, представляющие складываемые векторы, откладыва-

                                                                ются    от    одной     точки: , 

, ; на этих отрезках,

как на ребрах, строится параллелепипед (рис. 1.9). Вектор-сумма  является вектором , лежащим на диагонали этого параллелепипеда. 2.3. Вычитание векторов. Разностью векторов  и  называется такой вектор , что . Этот вектор всегда существует и определяется однозначно. Он обозначается  и вычисляется по правилу

,                                   (1.6)

т. е. для того чтобы найти разность векторов  и , необходимо к век-

тору  прибавить вектор, противоположный вектору  (рис. 1.10).

При решении геометрических задач векторным методом обыч-

C

A

A

B

                                            O               Рис. 1.10                         Рис. 1.11

но приходится выражать рассматриваемые векторы через векторы, отложенные от некоторой выбранной точки. Из равенства (1.1) следует, что для любых трех точек ,  и  

                                      (1.7)

(см. рис. 1.11).

 

             

§ 3. Умножение вектора на число

 

3.1. Определение произведения вектора на число. Произведением вектора  на действительное число  называется вектор , который удовлетворяет условиям:

(1)  ;

(2)  , если , если .^

Для обозначения произведения  вектора  на число  используют запись : .

Из этого определения следует, что произведение вектора на вещественное число является нулевым вектором в том и только в том случае, когда

, .

3.2. Свойства умножения вектора на число. Операция умножения вектора на число обладает следующими свойствами: 

1.                  Произведение вектора на число дистрибутивно относительно сложения векторов, т. е.

 

для любых векторов  и  и любого числа .

2.                  Произведение вектора на число дистрибутивно относительно сложения чисел, т. е.

 

для любых  и любого вектора .^

3.                  , для любого вектора  и любых чисел

           .

4.                   для любого вектора .

                                                   

^ В приведенном определении используется понятие длины вектора. Такой подход в школьном учебнике методически оправдан, т. к. ведет к значительному упрощению изложения. Можно, однако, как это делается при построении действительных чисел, последовательно определить произведения ), а затем, воспользовавшись

предельным переходом, – произведение , где  – произвольное действительное число.

^ Свойства 1 и 2 в школьных учебниках названы распределительными законами.

§ 4. Координаты вектора

 

4.1. Коллинеарные и компланарные векторы. Два вектора  и  называются коллинеарными, если существует прямая, которой они одновременно параллельны. Нулевой вектор считается коллинеарным любому вектору. Два вектора, не являющиеся коллинеарными, называются неколлинеарными. Для обозначения коллинеарности векторов  и  используется запись .

Три вектора ,  и  называются компланарными, если существует плоскость, которой они одновременно параллельны. В противном случае три вектора называются некомпланарными.

Если, по крайней мере, два из векторов ,  и  коллинеарны, то эти три вектора компланарны.

Пусть , ,…,  – данные векторы. Если вектор  предста

лен в виде , то говорят, что вектор  разложен по векторам , ,…, ; числа , ,…,  при этом называют коэффициентами этого разложения. Вектор  называют также линейной комбинацией векторов , ,…, , а числа , ,…,  – коэффициентами этой линейной комбинации.

Из условия (2) в определении произведения вектора на число следует, что любой вектор  и вектор  коллинеарны. Имеет место обратное утверждение.

Теорема 2. Если вектор  и ненулевой вектор  коллинеарны, то существует единственное число x такое, что

.                                        (1.8)

Из теоремы 2 следует, что если задан ненулевой вектор , параллельный прямой или лежащий на этой прямой, то любой вектор , параллельный этой прямой или лежащий на ней, может быть представлен в виде .

Для плоскости и пространства справедливы утверждения, аналогичные теореме 2.

Теорема 3. Пусть даны два неколлинеарных вектора  и , лежащие в плоскости  или параллельные ей. Тогда любой вектор

, также параллельный этой плоскости или лежащий на ней, может быть представлен в виде

,                                    (1.9)

и притом единственным образом.

Из теоремы 3 следует, что если векторы ,  и  компланарны, а векторы ,  при этом не коллинеарны, то вектор  единственным образом разлагается по векторам  и .

Теорема 4. Если векторы ,  и  некомпланарны, то любой вектор  может быть представлен в виде

,                            (1.10)

и притом единственным образом.

4.2. Определение координат вектора. В школьных

учебниках геометрии при введении координат вектора используется известная из курса алгебры прямоугольная декартовая система координат. В курсе планиметрии вводятся координаты вектора на плоскости, а в курсе стереометрии – координаты вектора в пространстве.

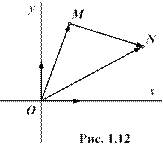
Чтобы задать прямоугольную декартовую систему  на плоскости выбирают две взаимно перпендикулярные прямые, на каждой из которых указывают положительное направление и единицу измерения отрезков. В геометрии направления и единичные отрезки координатных осей задают с помощью единичных векторов, которые называют координатными векторами. Координатный вектор оси абсцисс  обозначают , а координатный вектор оси ординат  

– : ,  (рис. 1.12).

Векторы  и  не коллинеарны,

поэтому на основании теоремы 3 любой вектор  может быть единственным образом разложен по координатным векторам:

. Коэффициенты ,  этого разложения называют коор-

динатами вектора  в системе координат ; при этом говорят

«вектор  имеет координаты ,  в системе координат » и пишут:  либо .

Вектор , где  – начало системы координат, называется радиусом-вектором точки  относительно точки . Если в системе координат  точка имеет координаты , , то эти же координаты имеет вектор : .

В пространстве координатный вектор оси аппликат  прямоугольной системы координат       обозначают ; здесь , , , , , . Векторы , ,  не компланарны, поэтому в силу теоремы 4 любой вектор  пространства может быть единственным образом разложен по координатным векторам: . Коэффициенты , ,  этого разложения назы-

вают координатами вектора  в системе координат ; при этом пишут:  либо .

4.3. Свойства координат векторов. Для векторов, заданных своими координатами в некоторой системе координат  на плоскости, справедливы следующие утверждения:

1.                   Равные векторы имеют равные координаты.

2.                   Координаты суммы (разности) векторов  и

 равны сумме (разности) соответствующих координат слагаемых (вычитаемых) векторов: .

3.                   При умножении вектора  на число  каждая его координата умножается на это число: .

Пусть точки ,  заданы своими координатами в системе координат . По определению разности векторов

. Поэтому из свойства 2 координат век-

торов следует, что .

Координаты векторов, заданных в системе координат  в пространстве обладают аналогичными свойствами.

 

§ 5. Скалярное произведение векторов

 

5.1. Угол между векторами. Пусть  и  – ненулевые векторы. От произвольной точки  отложим направленные отрезки  и , представляющие эти векторы. В том случае, когда лучи  и  не совпадают, за угол между векторами  и  принимают угол

 (рис. 1.13). В том случае, когда лучи  и  совпадают, угол между векторами  и  считают равным нулю. Это определение корректно, т. е. не зависит от выбора точки  (углы с сонаправленными сторонами равны). Угол между векторами  и  будем обозначать.

Два ненулевых вектора называются ортогональными, если угол между ними равен; пишут .

Нулевой вектор считается ортогональным любому вектору.

5.2. Определение скалярного произведения. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. Скалярное произведение векторов  и  обозначают  либо . Таким образом,

.                         (1.11)

Очевидно, что  тогда и только тогда, когда ; т. к.

нулевой вектор ортогонален любому вектору это утверждение справедливо и в том случае, когда хотя бы один из векторов  и  нулевой.

Поскольку  называют скалярным квадратом вектора  и обозначают . Следовательно,

.                                    (1.12)

Зная длины ненулевых векторов и их скалярное произведение, косинус угла между этими векторами можно найти по формуле

.                               (1.13)

5.3. Свойства скалярного произведения векторов.

Скалярное произведение векторов обладает следующими свойствами:

1.                  Скалярное произведение векторов коммутативно, т. е.

                                      (1.14)

для любых векторов  и .

2.                  Числовой множитель можно выносить за знак скалярного произведения, т. е.

,                        (1.15)

для любых векторов  и  и любого числа .

3.                  Скалярное произведение дистрибутивно относительно сложения векторов, т. е.

                             (1.16)

для любых векторов ,  и . 4. Скалярный квадрат вектора неотрицателен, т. е.

                                      (1.17)

для любого вектора ; при этом  тогда и только тогда, когда

.

5.4. Скалярное произведение векторов, заданных координатами. Пусть векторы  и  заданы своими координатами в некоторой прямоугольной декартовой системе координат

: , . Тогда

,                               (1.18)

.                                 (1.19) .                          (1.20)

Взяв в формуле (1.20) в качестве вектора  координатные векторы  и , получим

.                (1.21)

Возведем эти два равенства в квадрат и сложим по частям полученные соотношения, тогда с учетом (1.19) будем иметь:

.                         (1.22)

Если векторы ,  заданы своими

координатами в некоторой пространственной прямоугольной декартовой системе координат , то соответствующие формулы имеют аналогичный вид:

,                         (1.23)

,                              (1.24) .                   (1.25)

Поочередно взяв в формуле (1.25) в качестве вектора  координатные векторы , , , найдем:

, , .   (1.26)

Если возвести в квадрат эти три равенства, а затем сложить по частям, то с учетом (1.24) получим:

.          (1.27)

§ 6. Взаимосвязи векторного и координатного методов

 

6.1. Краткая историческая справка. Возникнув на основе жизненных потребностей человека, геометрия из разрозненного собрания конкретных практических рецептов постепенно оформилась в научную дедуктивную систему. Эта система, с одной стороны, хорошо отражает и описывает пространственные формы реальных предметов и отношения между ними, с другой – обладает богатым предметным языком и внутренней логической структурой. Именно в таком наглядно-доказательном виде она представлена в школьном курсе геометрии.

Школьная геометрия, хотя и опирается на наглядные соображения, строится как дедуктивная (доказательная) теория. Справедливость ее утверждений (теорем) устанавливается путем логических рассуждений, опирающихся на положения, истинность которых уже установлена. Понятно, что такая редукция утверждений не может быть бесконечной, некоторые исходные положения приходится принимать без доказательства. Этими исходными положениями являются аксиомы. В аксиомах раскрывается смысл основных геометрических объектов и отношений между ними. В качестве основных объектов школьного курса геометрии выбраны точка, прямая и плоскость, а в качестве основных отношений – «принадлежать», «лежать между», «быть равными». Все остальные геометрические понятия, вводятся (разъясняются) через основные и другие понятия, до этого уже рассмотренные.

Долгое время развитие геометрии шло за счет геометрического метода, т. е. истинность геометрических фактов и утверждений устанавливалась на основе аксиом и уже доказанных теорем с помощью логических рассуждений. Более того, первые алгебраические понятия также истолковывались геометрически. Например, решение квадратного уравнения сводилось к отысканию сторон прямоугольника с заданными периметром и площадью. Было установлено, что решение самых разнообразных практических геометрических задач сводится к решению алгебраических уравнений и их систем. Однако в алгебре долгое время отсутствовала удобная, привычная для нас символика, поэтому все алгебраические формулы излагались в сложной для восприятия и понимания словесной форме.

В конце XVI века французский математик Ф. Виет вводит для обозначения произвольных постоянных и переменных буквенные обозначения, а в начале XVII века его обозначения усовершенствует другой французский математик и философ, Р. Декарт. Появление буквенной символики способствовало становлению тригонометрии и общей теории алгебраических уравнений и их систем.

Полученные алгебраические результаты открыли пути для использования в геометрии различных вариантов вычислительного метода. Сущность этого метода состоит в том, что доказательство утверждений и вычисление неизвестных геометрических величин или отношений сводится к решению уравнений, неравенств или их систем, связывающих между собой заданные (известные) и неизвестные величины. Чтобы составить эти уравнения (неравенства, системы) используются известные геометрические факты и теоремы, содержание которых выражается на алгебраическом языке. Это одно из направлений широкого внедрения в геометрию аналитических методов.

Другим направлением тесной интеграции геометрии и алгебры стал метод координат, основы которого были заложены в работах Р. Декарта. Введение декартовой системы координат на плоскости устанавливает взаимно однозначное соответствие между точками этой плоскости и упорядоченными парами  действительных чисел. Так же точно введение декартовой системы координат в пространстве устанавливает взаимно однозначное соответствие между точками пространства и упорядоченными тройками  действительных чисел. Сущность метода координат состоит в том, что посредством координат точек изучаемые геометрические фигуры задаются аналитически с помощью уравнений, неравенств и их систем.

Пусть, например, фигура  расположена в плоскости с заданной на ней системой координат . Уравнение, неравенство или их система, которым удовлетворяют координаты любой точки фигуры  и не удовлетворяют координаты точек, не принадлежащих фигуре , называются условиями, определяющими фигуру  в данной системе координат . Аналогично определяются условия, определяющие фигуру  в декартовой системе координат  в пространстве. Метод координат позволяет по условиям, оп-

ределяющим фигуру  в данной системе координат, аналитически изучать ее геометрические свойства. Это зачастую существенно упрощает рассуждения и позволяет доказывать теоремы и вычислять неизвестные величины, используя определенные алгоритмы.

По мере становления алгебры и начал анализа дальнейшее развитие геометрии идет преимущественно аналитическими методами. Метод координат находит свое окончательное оформление в разделе геометрии, который называется аналитической геометрией.

Метод координат, несомненным достоинством которого является алгоритмизация процесса решения многих геометрических задач, имеет и свои слабые стороны. Они проявляются, например, в том, что в ходе промежуточных аналитических выкладок теряется геометрическое содержание задачи, выражение в координатной форме простых геометрических фактов зачастую имеет сложную для восприятия форму, реализация алгоритмов связана порой с громоздкими вычислениями, которые могут привести к ошибке и т. д. Поэтому еще на заре становления аналитической геометрии математики высказывали мысли о необходимости создания геометрического исчисления, позволяющего оперировать с геометрическими объектами так же, как с численными величинами.

Векторная алгебра, элементами которой являются направленные отрезки, стала одним из воплощений этой идеи. Впервые термин «вектор» появляется в середине XIX веке в работах немецкого математика Г. Грассмана и ирландского математика У. Гамильтона. Современный вид векторному исчислению к концу XIX века придают американский физик Д.В. Гиббс и английский физик О. Хевисайд. Уже в начале XX века векторы становятся незаменимым средством исследований в различных областях математики и физики. В области геометрии этому во многом способствовала книга «Пространство, время, материя» выдающегося немецкого математика Г. Вейля, вышедшая в 1918 году. Во вводной главе этой книги приведена аксиоматика евклидовой геометрии, в основе которой лежат понятия «точка» и «вектор», а связь между ними установлена с помощью операции откладывания вектора от точки. Подход Г. Вейля оказался удивительно плодотворным и позволил за счет незначительных модификаций строить аксиоматики различных неевклидовых геометрий и их многомерные обобщения.

В 40-х годах прошлого века векторная алгебра становится обязательным элементом отечественного высшего математического образования, а 60-е годы векторы появляются в курсах геометрии для средней школы.

Так же как для чисел и буквенных выражений для векторов определены алгебраические операции: сложение и вычитание, умножение вектора на число, скалярное умножение векторов, т. е. множество векторов вместе с определенными на нем операциями тоже является алгеброй, эта алгебра называется векторной. В некотором смысле векторная алгебра по своему содержанию более близка к геометрии, чем привычная школьная алгебра; и векторы, и операции над ними определены на базе геометрических понятий. Поэтому естественно ожидать, что использование векторной алгебры даст новый достаточно универсальный метод решения геометрических задач.

Суть векторного, как и любого алгебраического метода, состоит в том, что первоначально условия геометрической задачи и требуемый результат описываются на алгебраическом языке (в данном случае, на языке векторной алгебры), т. е. строится векторная модель задачи. Для того чтобы продуктивно решать геометрические задачи векторным методом, необходимо научиться задавать с помощью векторов основные геометрические объекты и описывать основные отношения между ними на языке векторной алгебры. Не менее важно видеть возможность обратного перехода от векторной модели к описываемым ею геометрическим объектам и отношениям между ними, т. е. уметь строить геометрические интерпретации алгебраических векторных соотношений.

6.2. Базис. Координаты вектора в базисе. Важнейшими понятиями векторной алгебры являются понятия вектора, векторного пространства, линейной зависимости векторов и базиса векторного пространства.

Непустое множество  называется векторным пространством, а его элементы – векторами, если на множестве  определены операции сложения векторов и умножения вектора на действительные числа, удовлетворяющие следующим условиям (аксиомы векторного пространства):

1.        Для любых векторов ,  и  

.

2.        Для любых векторов  и  

.

3.        Существует вектор  (нуль-вектор) такой, что для любого вектора  

.

4.        Для каждого вектора  существует вектор  (противоположный вектор) такой, что

.

5.        Для любых действительных чисел ,  и любого вектора  

.

6.        Для любых действительных чисел ,  и любого вектора  

.

7.        Для любого числа  и любых векторов

                                                   .

8.        Для любого вектора  

.

Свойства операций сложения векторов и умножения вектора на число, рассмотренные в школьном курсе геометрии, позволяют заключить, что множество всех векторов пространства является векторным пространством. Нетрудно доказать, что векторным пространством будет множество векторов, образованное векторами, лежащими в некоторой плоскости , и векторами, ей параллельными. Так же точно, векторным пространством является и множество векторов, лежащих на прямой , и векторов, ей параллельных. Система векторов

                                      (1.28)

называется линейно зависимой, если существуют числа , , …, , среди которых хотя бы одно отлично от нуля, такие, что

.                       (1.29)

Если же векторное равенство (1.29) выполняется тогда и только тогда, когда все числа , , …,  равны нулю, то система векторов (1.28) называется линейно независимой.

Очевидно, что система, состоящая из одного вектора , будет линейно зависимой тогда и только тогда, когда этот вектор нулевой. Используя теоремы 2-4, самостоятельно докажите следующие утверждения:

1)                 система векторов ,  линейно зависима тогда и только тогда, когда эти векторы коллинеарны;

2)                 система векторов , ,  линейно зависима тогда и только тогда, когда эти векторы компланарны;

3)                 любая система, состоящая более чем из трех векторов, линейно зависима.

Система векторов, взятых в определенном порядке, называется базисом векторного пространства, если:

(а) эта система линейно независима;

(б) любой вектор пространства можно представить в виде линейной комбинации векторов данной системы.

Число векторов, входящих в базис, называется размерностью векторного пространства.

Пусть  – векторное пространство, состоящее из всех векторов пространства. Если , ,  – некомпланарные векторы, то они линейно независимы, а по теореме 4 любой вектор  пространства может быть единственным образом разложен по векторам , , . Поэтому система векторов , , , взятых в указанном порядке, является базисом векторного пространства  и это пространство является трехмерным. В качестве базиса векторов пространства можно взять любую упорядоченную тройку некомпланарных векторов.

Базис, образованный векторами , , , будем обозначать

, сами векторы , ,  называть базисными векторами, а разложение

 

– разложением вектора  по базисным векторам. Числа  при этом называют координатами вектора  в базисе  и, как обычно, пишут:  либо .

Векторы , ,  можно упорядочить шестью различными способами, т. е. с помощью одной тройки некомпланарных векторов можно задать шесть различных базисов множества векторов пространства. Например, базис  отличен от базиса , в нем .

Базис , образованный единичными попарно ортогональными векторами , называется ортонормированным.

Из теоремы 4 следует, что если в векторном пространстве  задан базис , то любой вектор  имеет в этом базисе определенные координаты . Обратно, всякая упорядоченная тройка действительных чисел  определяет в базисе  единственный вектор .

Таким образом, выбрав в пространстве произвольную точку  и некоторый базис , любую точку  пространства можно однозначно задать координатами ее радиус-вектора  в выбранном базисе. Это позволяет с помо-

щью векторов решать геометриче- z ские задачи «в координатах», т. е. M

почти так же точно, как координатным методом. Можно пойти еще дальше, ввести систему координат

. Для этого проведем через точку  три прямые, параллельные векторам ,  и . Примем точку  за

начало координат. С помощью век-          ^{Рис. 1.14} тора  зададим положитель-

ное направление на первой прямой и примем ее за ось абсцисс ; с помощью вектора  зададим положительное направление на второй прямой, примем ее за ось ординат ; наконец, с помощью вектора  зададим положительное направление на третьей прямой, ее примем за ось аппликат  (рис. 1.14). Построенная система координат называется аффинной. 

Аналогично, пусть  – векторное пространство, образованное векторами, лежащими в некоторой плоскости  и векторами, ей параллельными; ,  – неколлинеарные векторы из . Тогда векторы являются линейно независимыми, и по теореме 3 любой вектор  может быть единственным образом разложен по векторам , . Поэтому упорядоченная пара  является базисом векторного пространства , а само это пространство является двумерным. В качестве базиса пространства  можно взять любую упорядоченную пару неколлинеарных векторов из этого пространства. Базисы  при этом являются различными.

Числа ,  в разложении  вектора  по базис-

ным векторам  и  называют координатами вектора  в базисе

, пишут:  либо .

Базис , образованный единичными ортогональными векторами, называется ортонормированным.

Если в векторном пространстве  задан базис , то любой вектор  имеет в этом базисе определенные координаты

. Обратно, всякая упорядоченная пара  действительных чисел определяет в базисе  единственный вектор  пространства .

Выбирая на плоскости произволь-

                         ^y                               ную точку  и некоторый базис ,

можно задать на этой плоскости аффинную систему координат  (рис. 1.15).

Наконец, пусть  – векторное пространство, состоящее из векторов, ле-

_{Рис. 1.15} жащих на некоторой прямой l, и векторов, ей параллельных;  – любой нену-

левой вектор этого пространства. Тогда система, состоящая из вектора , является линейно независимой, а любой вектор  может быть единственным образом представлен в виде . Следовательно,  – одномерное векторное пространство и  – его базис. Число  называется координатой вектора  в базисе .

Если задан ненулевой вектор , то любой коллинеарный ему вектор , имеет в базисе  определенную координату . Обратно, всякое действительное число  определяет в базисе  единственный вектор , коллинеарный вектору .

 

Задачи для повторения

 

1.                  Докажите, что равенство  имеет место тогда и только тогда, когда . Как расположены точки  и , если точки  и  совпадают?

2.                  Как расположены точки ,  и , если ?

3.                  Точка  симметрична точке  относительно точки . Точки  и  получены в результате откладывания вектора  от точек  и

. Докажите, что .

4.                  Дано:. Докажите, что .

5.                  Дан правильный шестиугольник , точка  – его центр          ,

, , , , ,  укажите векторы: а) равные вектору ; б) противоположные вектору ; в) сонаправленные с вектором ; г) противоположно направленные с вектором .

6.                  Докажите, что: а) , б) .

7.                  Упростите выражения:

а) ;

б)

в) .

8.                  Докажите, что сумма векторов, общим началом которых является центр правильного n-угольника, а концами – его вершины, равна нуль-вектору.

9.                  Как расположены точки ,  и , если: а) ,

б) ?

10.              Дано: , . Выразите через векторы  и  векторы: а) .

11.              Дан тетраэдр

через векторы ,  и  векторы: а) ,

в).

Решение. в) В силу (1.7) имеем:

 

12.              Точка  является точкой пересечения диагоналей параллелепипеда , точки , , ,  принадлежат ребрам

, , ,  соответственно; причем ,

, , . Разложите по векторам

, д) , е) , ж) , з) , и) , к) , л) , м) ,

н) . Выясните, лежат ли точки , , ,  в одной плоскости.

13.              Докажите, что векторы  и  коллинеарны тогда и только тогда, когда существует линейная комбинация этих векторов, равная нулевому вектору, в которой хотя бы один из коэффициентов отличен от нуля.

14.              Докажите, что векторы ,  и  компланарны тогда и только тогда, когда существует линейная комбинация этих векторов, равная нулевому вектору, в которой хотя бы один из коэффициентов отличен от нуля.

15.              Векторы ,  заданы своими коорди-

натами в системе координат . Докажите, что векторы  и  коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны.

16.              Докажите, что:

; .

17.              Найдите длину вектора .

18.              Дан треугольник . Докажите, что вектор  лежит на биссектрисе угла , а вектор  – на биссектрисе внешнего угла треугольника при вершине .

19.              Дан трехгранный угол  с вершиной . Выясните, где расположен вектор .

20.              Векторы  и  заданы своими координатами в прямоугольной декартовой системе координат . Докажите, что

.                          (1.30)

21.              Векторы ,  заданы своими ко-

ординатами в прямоугольной декартовой системе координат . Докажите, что

 

Глава II

 

АФФИННЫЕ ЗАДАЧИ

 

§ 2.1. Опорные аффинные задачи и формулы

 

Для того чтобы научиться решать геометрические задачи векторным методом, надо уметь описывать (задавать) с помощью векторов геометрические фигуры и отношения между ними. В этом параграфе приводится «техническое оснащение», необходимое для решения аффинных задач. При этом выделяются задачи и формулы, которые наиболее часто служат основой для решения других, более сложных, задач. Такие задачи и формулы, как отмечено во введении, называют ключевыми или опорными.

Точки фигур, рассматриваемых в задачах, будем задавать с помощью векторов, отложенных от некоторой фиксированной точки, например, . Иными словами, точка  фигуры определяется радиус-вектором  точки  относительно точки .

Прямая чаще всего задается двумя ее точками, а плоскость – тремя точками, не лежащими на одной прямой. Поэтому ограничимся только этими способами задания прямой и плоскости (любые другие способы их задания легко сводятся к указанным).

2.1.1. Принадлежность точки прямой (плоскости). Пусть прямая задана точками  и . Из определения коллинеарных векторов следует, что точка  принадлежит прямой  тогда и только тогда, когда вектор  коллинеарен ненулевому вектору  

(рис. 2.1). Это условие можно записать так:

.                  (2.1)

Пусть точки ,  и  заданы их радиус-векторами, относительно точки . Тогда по определению разности

векторов равенство (2.1) можно пере- O Рис. 2.1 писать в виде:

.    (2.2)

Опорной задачей, описывающей условия принадлежности точки прямой, является

Задача 2.1. Докажите, что точка  принадлежит прямой  тогда и только тогда, когда для любой точки  выполняются равенства:

,                                 (2.3) .                                       (2.4)

Решение. Пусть точка  принадлежит прямой . Тогда векторы  и  коллинеарны. Поскольку , имеет место равенство (2.1), в котором  – однозначно определенное действительное число, а значит, для произвольной точки справедливо равенство (2.2). Из (2.2) следует, что . Введя обозначение , получаем равенства (2.3), (2.4), которые требуется доказать.

Обратно, пусть для точек , ,  и произвольной точки О выполняются равенства (2.3) и (2.4). Докажем, что точка  принадлежит прямой . Для осуществления этого доказательства все рассуждения необходимо провести в обратном порядке.

Из равенства (2.4) , поэтому векторное равенство (2.3) можно переписать в виде: . Отсюда следует, что , и по определению разности векторов имеем: . Поэтому векторы ,  коллинеарны, и значит, . □

                                _O                                                Из определения компланар-

ных векторов следует, что точка  принадлежит плоскости  

тогда и только тогда, когда вектор  компланарен неколлинеарным векторам  и  (рис. 2.2). Условие компланарности этих векторов можно записать Рис. 2.2            так:

.      (2.5)

Если точки , ,  и  заданы векторами, отложенными от точки О, то равенство (2.5) можно переписать в виде:

.               (2.6)

Опорной задачей, описывающей условия принадлежности точки  плоскости , будет задача 2.2, решение которой является достаточно простой (при этом типичной в условиях применения векторного метода) трансформацией решения задачи 2.1.

Задача 2.2. Докажите, что точка  принадлежит плоскости  тогда и только тогда, когда для любой точки О выполняются равенства:

,                           (2.7) .                                    (2.8)

Решение. Пусть точка  принадлежит плоскости . Тогда векторы ,  и  компланарны. Точки не лежат на одной прямой (задают плоскость), поэтому векторы  и  не коллинеарны. Следовательно, имеет место равенство (2.5), в котором  и  – однозначно определенные действительные числа. Выбрав произвольную точку , от равенства (2.5) можно перейти к равенству (2.6). Равенство (2.6), в свою очередь, перепишем в виде:

.

Введя обозначение , получим соотношения (2.7),

(2.8), которые требуется доказать.

Для доказательства обратного утверждения вновь все рассуждения необходимо провести в обратном порядке. □

2.1.2. Взаимное расположение двух прямых. Пусть даны прямые  и . Очевидно, что эти прямые будут параллельны тогда и только тогда, когда векторы  и  коллинеарны, а вектор  им не коллинеарен (рис. 2.3); прямые адать тогда и только тогда, когда все три вектора ,  и  попарно коллинеарны (рис. 2.4).

Если векторы  и  не коллинеарные, то прямые  и  либо скрещиваются, либо пересекаются. В первом случае тройка векторов  некомпланарна (рис. 2.5). Во втором случае вектор  компланарен векторам  и  (рис. 2.6).

2.1.3. Взаимное расположение прямой и плоскости. Пусть даны прямая  и плоскость . Прямая будет пересекать плоскость, если векторы ,   не являются компланарными

(рис. 2.7).

Если вектор  компланарен векторам  и , то прямая  либо параллельна плоскости A, либо лежит в этой плоскости. В первом случае вектор  не компланарен векторам  и  (рис. 2.8), во втором – компланарен (рис. 2.9).

2.1.4. Взаимное расположение двух плоскостей. Пусть даны плоскости  и . Плоскость  будет параллельна плоскости  тогда и только тогда, когда каждый из векторов ,  будет компланарен векторам , , а вектор  – нет (рис. 2.10). Если вектор  также компланарен векторам , , плоскости  и  совпадают (рис. 2.11).

В том случае, когда хотя бы один из векторов ,  не компланарен векторам ,  плоскости ,  пересекаются

(рис. 2.12).

2.1.5. Деление отрезка в данном отношении. Пусть  и  – две различные точки прямой и  – такая точка этой прямой, что

.                                     (2.10)

Тогда говорят, что точка  делит отрезок  в отношении , считая от точки ; число  при этом называют отношением трех точек , В и . В литературе по геометрии для обозначения отношения  трех точек прямой обычно употребляются записи: ,

. Мы будем использовать второе из этих обозначений.

Если точка  лежит между точками  и , то векторы  и  сонаправлены, при этом . В этом случае точка  делит отрезок  внутренним образом (рис. 2.13 а).

Если , то .

Если точка  лежит вне отрезка , то векторы  и  направлены противоположно, а  (рис. 2.13 б). В данном случае

говорят, что точка  делит отрезок  внешним образом. Поскольку при этом либо , либо , то .

Очевидно также, что

.

В самом деле, пусть , тогда . 

Пусть точки ,  и  заданы векторами, отложенными от некоторой точки , тогда равенство (2.10) можно переписать в виде:

. Отсюда , и значит,

.                             (2.11)

Если теперь провести все рассуждения в обратном порядке, то мы вернемся к формуле (2.10). Следовательно, точка  делит отрезок  в данном отношении  () тогда и только тогда, когда для

любой точки  имеет место соотношение (2.11).

Формулу (2.11) называют формулой деления отрезка в данном отношении. Эта формула при использовании векторного метода употребляется особенно часто, поэтому ее следует включить в число опорных.

Не менее часто применяется формула деления отрезка пополам, которая получается из (2.11) при . В этом случае , и, следовательно, . Таким образом, точка  является серединой отрезка  тогда и только тогда, когда для любой точки  

.                                (2.12)

Во многих задачах внутренняя точка  отрезка  задается с помощью отношения длин отрезков  и . Если ,

; формула (2.11) принимает вид:

.                           (2.13)

Примечание. Для любого действительного числа  на прямой  существует одна и только одна точка , которая делит отрезок  (считая от точки А) в данном отношении .

В самом деле, из формулы (2.10) имеем:  или . Так как , то отсюда получаем:

.

Таким образом, для того, чтобы построить на прямой  точку , которая делит заданный отрезок  в отношении , считая от точки , достаточно выбрать вектор  в качестве единичного вектора этой прямой. В системе координат  точка  имеет координату .

Задача 2.3. На прямых  и , содержащих стороны треугольника , взяты соответственно точки  и , которые делят стороны треугольника в отношениях

, .

Докажите, что при любом выборе точки  радиус-вектор  точки пересечения прямых  и  имеет вид:

.

Решение. Согласно опорной задаче 2.1 при любом выборе точки  имеем:

.

Выразим векторы  через векторы , ,  и подставим

в эти соотношения. По формуле деления отрезка в данном отношении . Поэтому, с одной стороны,

 

С другой стороны,

 

Если точка  не лежит в плоскости треугольника , то векторы

, ,  не компланарны; тогда из разложений вектора  получим

.

Отсюда

 

Решая эту систему относительно  и , находим:

.

Остается подставить любое из найденных значений в соответствующее разложение вектора . Например,

 

Когда точка  лежит в плоскости треугольника , возьмем точку , не лежащую в этой плоскости. Тогда  и

 

. □

Задача 2.4. Прямые  и  пересечены тремя параллельными прямыми в точках , ,  и , ,  соответственно. Докажите, что .

Решение. Из условия задачи следует, что , .

                                                            Пусть      ,      ,

, . Требуется доказать, что .

Если точки  не совпадают, то векторы  и  не коллинеарны.

                           Рис. 2.14                  Разложим по этим векторам векторы

. Прибавим к обе-

им частям равенства  вектор , тогда .

Отсюда

.

По правилу треугольника с учетом условий задачи получим:

,       

. Поэтому

,

 

      Равенство  перепишется теперь следующим образом 

 

Отсюда по теореме о единственности разложения вектора по двум неколлинеарным векторам Из первого равенства  и, следовательно, .

Заметим, что попутно из второго равенства можно найти соотношение, связывающее .

Если точки  и  совпадают, то треугольники  и  подобны с коэффициентом подобия . В этом случае

,  

и , т.е. . □

Примечание. Следствием доказанного утверждения является теорема Фалеса: если на одной стороне угла отложены равные отрезки и через их концы проведены параллельные прямые, пересекающие другую сторону угла, то высекаемые на ней отрезки также равны.

2.1.6. Отношение отрезков параллельных прямых. Пусть отрезки  и  лежат либо на параллельных прямых, либо на одной прямой. Рассмотрим коллинеарные векторы , и .

Существует единственное действительное число  такое, что

. Это число называют отношением коллинеарных векто-

ров (отношением параллельных отрезков). Из определения произведения вектора на число следует: , если ;

, если .

Задача 2.5. Параллельные прямые  и  пересечены тремя прямыми, проходящими через одну точку, в точках , ,  и ,

,  соответственно. Докажите, что .

Решение. Пусть  – общая точка секущих прямых. Рассмотрим гомотетию с центром , которая переводит точку  в точку . В этой гомотетии точка  перейдет в точку , точка  – в точку . Если векторы ,  сонаправлены (рис. 2.15, а), то коэффициент гомотетии  и равен ; если векторы ,  направлены противоположны (рис. 2.15, б), то коэффициент гомотетии  и равен . В обоих случаях

.

Рис. 2.15

Отсюда  или

, .

Пусть , тогда . Следовательно, . □

Рассмотренные векторные условия и формулы дают возможность, используя аппарат векторной алгебры: 

1)   установить принадлежность трех точек одной прямой (четырех точек одной плоскости);

2)   выяснять взаимное расположение прямых, отрезков, плоскостей, в частности, доказывать их параллельность, устанавливать, что три прямые проходят через одну точку и т. п.;

3)   вычислять отношение трех точек прямой;

4)   находить отношение длин параллельных отрезков и т. д.

Примечание. При решении геометрических задач векторным методом прямую часто удобно задавать точкой и параллельным ей вектором.

Действительно, если задан ненулевой вектор  и точка , то через точку  проходит единственная прямая , параллельная вектору . Прямую в

этом случае обозначают , а вектор  называют ее направляющим вектором.

Так же точно плоскость  задают ее точкой  и парой неколлинеарных векторов  и , параллельных этой плоскости; плоскость при этом обозначают , а векторы ,  называют ее направляющими векторами.

             

§ 2.2. Применение опорных задач и формул

 

2.2.1. Формула деления отрезка пополам. Наиболее простыми и часто встречающимися аффинными задачами являются задачи, в которых фигурируют середины отрезков, деление отрезка пополам, симметричные точки. При решении этих задач векторным методом используется формула деления отрезка пополам. Это объясняется тем, что в основе сложения векторов лежит «правило параллелограмма», а диагонали параллелограмма, как известно, в точке их пересечения делятся пополам. 

Поэтому формула деления отрезка пополам незаменима при решении задач, в которых рассматриваются параллелограммы, средние линии, симметричные точки. Рассмотрим примеры таких задач.

Пример 2.2.1. Точки  и  являются соответственно серединами сторон  и  четырехугольника . Докажите, что середины диагоналей четырехугольников  и  являются вершинами параллелограмма либо лежат на одной прямой.

Решение. Пусть ,  – середины диагоналей ,  четырехугольника , а ,  – середины диагоналей ,  четырехугольника  (рис. 2.14).

В силу формулы деления от- C резка пополам

                                       ,      B

где  – произвольная точка.

Применяя эту же формулу к точкам , , ,  и учитывая записанные соотношения, последвательно получаем: о-         A             _{Рис. 2.14}

,

,

, .

Откуда

, .

Итак, . Отсюда следует, что длины отрезков  и  равны, а сами отрезки лежат либо на параллельных прямых, либо на одной прямой. В первом случае четырехугольник  является параллелограммом (его противоположные стороны равны и параллельны), во втором – точки , , ,  принадлежат одной прямой. □

Пример 2.2.2. Докажите, что отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаются в одной точке и делятся этой точкой пополам^[2].

Решение. Рассмотрим тетраэдр . Середины его противоположных ребер ,  обозначим буквами ,  соответственно, середины противоположных ребер ,  – буквами , , а середины противоположных ребер ,  – буквами , . Пусть  – произвольная точка. По формуле деления отрезка пополам:

, .

Нетрудно заметить, что

.

Отсюда следует, что середины отрезков , определяемые векторами , совпадают, т. е. отрезки пересекаются в одной точке и делятся ею пополам. □

Примечание. Отрезок, соединяющий середины противоположных ребер тетраэдра, называется бимедианой.

Пример 2.2.3. Даны треугольник  и точка

, лежащая в плоскости этого треугольника. Докажите, что точки, симметричные данной точке  

относительно середин сто-

рон треугольника , являются вершинами треугольника, центрально-симметричного данному.

Решение. Точки, симметричные точке  относительно середин

, ,  сторон , , , обозначим буквами , ,  соответственно (рис. 2.15).

Точка  является серединой отрезка  и серединой отрезка

, поэтому

.

Отсюда следует, что

2.

Аналогично находятся векторы

, .

Теперь нетрудно заметить, что векторы

,

,

,

определяющие середины отрезков , ,  соответственно,

равны между собой. Это означает, что середины этих трех отрезков

совпадают, а треугольники  и  являются центральносимметричными. □

В заключение рассмотрим доказательство признака трапеции.

Пример 2.2.4. Точки ,  являются соответственно серединами сторон,  выпуклого четырехугольника . Продолжения сторон  и  пересекаются в точке . Докажите,    что        четырехугольник  является трапецией тогда и только тогда, когда точки ,  и  

       лежат на одной прямой.                            _D

Решение. Пусть  – трапеция с основаниями  и ,  – се-

редина ,  – середина  подобен треугольнику , поэтому , . Сложим эти два равенства:

.

По формуле деления отрезка пополам

.

Следовательно, , и, значит, точки M, N и P лежат на одной прямой.

Обратно, пусть для некоторого выпуклого четырехугольника

, описанные в условии задачи точки ,  и  лежат на одной прямой. Докажем, что этот четырехугольник является трапецией.

Имеем три пары коллинеарных векторов  и ,  и ,  и . Следовательно, существуют числа , ,  такие, что

, , . Учитывая же, что точки ,  являются серединами сторон ,  четырехугольника, имеем:

. С другой

стороны, . Поскольку разложение вектора  по неколлинеарным векторам  и  является единственным, приходим к соотношениям: .

Итак, , . Отсюда , т.е. . Следовательно, стороны ,  четырехугольника  параллельны, а стороны ,  не параллельны, и он явля-

ется трапецией с основаниями , . □

2.2.2. Использование опорных задач и формулы деления отрезка в данном отношении. Рассмотрим различные типы аффинных задач, при решении которых применяются опорные задачи 2.1, 2.2 и формула деления отрезка в данном отношении.

Пример 2.2.5. Основанием четырехугольной пирамиды  служит параллелограмм . Точки , ,  принадлежат ребрам , ,  соответственно и делят эти ребра в отношениях

, , , считая от вер-

S                                                  шины  пирамиды. Пересекает ли плоскость  ребро

? Если да, то в каком отношении она делит это ребро?

C Решение. Поскольку точ-

ки , , ,  не лежат в одной плоскости, векторы ,   не компланарны (рис. 2.17).

^A            Рис. 2.17              ^D            Выразим через них векторы , ,  и . Из условий задачи следует, что

.

По определению суммы и разности векторов

 

.

Пусть плоскость  пересекает прямую  в точке , тогда

. Поэтому .

С другой стороны, согласно опорной задаче 2.2

,

где . Заменяя векторы , ,  коллинеарными им векторами, получим

.

На основании единственности разложения вектора  по некомпланарным векторам , ,  заключаем, что

.

Отсюда . Так как сумма  равна 1, то , и значит, . Поскольку , точка  делит отрезок  внешним образом. Следовательно, плоскость  ребро  не пересекает. □

Пример 2.2.6. Даны два параллелограмма  и ,

причем вершины  и  второго параллелограмма лежат на сторонах  и  соответственно первого. Прямые  и  пересекаются в точке . Докажите, что

точки , ,  лежат на одной ^{D C} прямой и найдите отношение, в котором точка  делит отрезок

, считая от точки . Когда точка  будет серединой от-

       резка ?                                        A                           _M                B

                Решение.           Поскольку

          и  – параллело-                             Рис. 2.18

граммы, то

, .

Кроме того, из условия задачи следует, что , , и значит,

.

В силу опорной задачи 2.1 точка  принадлежит прямой  

тогда и только тогда, когда 

, .

Прямой же  эта точка принадлежит при выполнении условий

.

Заменяя векторы коллинеарными им векторами , , будем иметь: . Отсюда следует, что , . Поэтому ,  можно выразить через ,  из следующей системы:

 

Решая систему, находим, что . Следовательно,

.

Вычислим теперь векторы          и :

                      

,

.

Отсюда следует, что . Таким образом, точки , ,  лежат на одной прямой и точка  делит отрезок  в отношении . Точка  будет серединой отрезка  тогда и только тогда, когда это отношение равно 1, т.е. при условии . □

Пример 2.2.7. Прямая, проходящая через вершину  треугольника , пересекает медиану  в точке , а сторону  – в точке . Найдите отношения  и , если  

.

Решение. Пусть . В силу формулы (2.13)

, .

Так как В₁ – середина стороны , то первое равенство можно переписать так:

.

Поскольку вектор  коллинеарен вектору ,

.

Сравнивая       два       разложения вектора  по двум неколлинеарным векторам     и        , получим:

.

Разделив второе из полученных

равенств на первое, находим, что . Отсюда , и значит,

.

Теперь разделим на  числитель и знаменатель левой части второго из рассматриваемых равенств: . Подставив в это равенство найденное значение , получим ; откуда

. Таким образом, . Представив вектор  

в виде , имеем: . Отсюда находим, что . По определению произведения вектора на

число . □

Пример 2.2.8. Прямые  и  пересечены четырьмя прямыми, проходящими через одну точку, в точках , , ,  и , , ,  соответственно (рис. 2.20). Докажите, что .

Решение. Пусть  – общая точка секущих прямых. Через точки  и  проведем прямые, параллельные прямой . Точки пересечения этих прямых с прямыми ,  обозначим ,  и ,  соответственно.

Согласно опорной задаче 5 .

Из подобных треугольников  и ,  и  соответственно имеем:

.

Почленным делением этих равенств получим:

 

или, учитывая порядок точек,

.

        _{1                         1                                                      1}            Из     подобных     треугольников

 и ,  и  

                                  ^{Рис. 2.20}                    аналогично находим:

.

Таким образом, . □

 

Задачи для самостоятельного решения

 

22.                Докажите, что средние линии любого четырехугольника точкой их пересечения делятся пополам.

23.                Докажите, что две противоположные стороны четырехугольника параллельны тогда и только тогда, когда отрезок, соединяющий их середины, проходит через точку пересечения диагоналей.

24.                Докажите, что четырехугольник является параллелограммом тогда и только тогда, когда отрезки, соединяющие середины его противоположных сторон, проходят через точку пересечения диагоналей.

25.                Через две противоположные вершины параллелограмма проведены прямые, пересекающие его стороны или их продолжения. Докажите, что полученные при этом четыре точки являются вершинами трапеции или параллелограмма.

26.                Докажите, что четырехугольник  является параллелограммом тогда и только тогда, когда

,

где  – произвольная точка.

27.                Докажите, что, как бы ни были расположены в пространстве параллелограммы  и , середины отрезков, соединяющих их соответственные вершины, также являются вершинами параллелограмма или лежат на одной прямой.

28.                Даны четыре точки A, ,  и . Точки K, , , N, ,  являются серединами отрезков , , , , ,  соответственно. Докажите, что отрезки , ,  имеют общую середину.

29.                Даны четырехугольник и точка. Докажите, что точки, симметричные данной точке относительно середин сторон четырехугольника, являются вершинами параллелограмма.

30.                Докажите, что середины диагоналей четырехугольника симметричны относительно точки пересечения его средних линий.

31.                На одной прямой взяты точки , , …,  так, что , а на второй прямой – точки , ,

…,  так, что . Докажите, что середины отрезков , , …,  расположены на одной прямой.

32.                Дана ломаная . Докажите, что если середины отрезков , , …,  лежат на одной прямой, то точки , , …,  лежат на одной прямой и точки , , …,  также лежат на одной прямой.

33.                На сторонах ,  треугольника  взяты точки ,  такие, что . Отрезки  и  пересекаются в точке

. В каком отношении точка  делит каждый из этих отрезков?

34.                Дан параллелограмм . Точки ,  делят отрезки ,  так, что , . Прямые  и  пересекаются в точке . Найдите отношения  и .

35.                Дан параллелограмм  и точки , ,  такие, что

, , . При каком соотношении между

, ,  точки , ,  лежат на одной прямой?

36.                Основания  и  трапеции  равны  и . На боковых сторонах AD и  взяты соответственно точки  и  так, что . Докажите, что отрезок  параллелен основаниям

трапеции и найдите его длину.

37.                Через вершину  параллелограмма  проведена прямая, пересекающая диагональ  в точке , прямую  в точке  и прямую  в точке . Докажите, что .

38.                Точки , ,  делят стороны треугольника  в отношениях , , ; . Найдите отношение площади треугольника  к площади треугольника .

39.                Точки ,  и  делят ребра , ,  куба

 в отношении , считая от вершины . Найдите

отношение, в котором плоскость  делит диагональ  куба.

40.                Дан параллелепипед . Точка  делит ребро  в отношении 1:4, считая от вершины , а точка  – ребро  

в отношении 3:1, считая от вершины ,  – точка пересечения диагоналей грани . Постройте сечение параллелепипеда плоскостью . В каких отношениях эта плоскость делит ребра ,  и диагонали параллелепипеда? 

41.                Дан тетраэдр . Точки ,  и  принадлежат ребрам

, ,  соответственно; причем ,

. Найдите отношение, в котором плоскость  

делит ребро .

42.                Секущая плоскость пересекает ребра , ,  треугольной пирамиды  в точках ,  и  соответственно; причем , . В каком отношении должна делить

ребро  точка , чтобы объемы многогранников, на которые разбита пирамида секущей плоскостью, были равны?

43.                Основанием усеченной пирамиды  является параллелограмм , сторона верхнего основания пирамиды вдвое меньше стороны нижнего основания. Через вершину , середину ребра  и точку  ребра  проведена секущая плоскость. Найдите отношение, в котором эта плоскость делит ребро

, если .

44.                Секущая плоскость пересекает ребра , ,  треугольной пирамиды  в точках ,  и  соответственно; причем

, , . В каком отношении

эта плоскость делит объем пирамиды?

 

             

§ 2.3. Медианы треугольника и тетраэдра

 

Традиционно при изучении векторного метода рассматривается большое число задач, посвященных четырем замечательным точкам треугольника. Поскольку лишь одна из них – точка пересечения медиан – носит аффинный характер, в этой главе будут рассмотрены ключевые задачи и формулы, связанные с этой точкой.

2.3.1. Опорные задачи и формулы. Начнем с векторного доказательства хорошо известной теоремы Архимеда.

Задача 2.6. Докажите, что медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершин.

Решение. Пусть медианы ,  треугольника  пересекаются в точке  (рис. 2.21). Докажем, что: 1) третья медиана  треугольника также проходит

через точку ; 2) точка  

A

делит все три медианы в отношении 2:1, считая от вершин треугольника.

По условию точки , ,  – середины сторон ,  и  соответственно, поэтому

,

где  – произвольная точка. Точка  принадлежит каждой из прямых , , следовательно, по формуле деления отрезка в дан-

ном отношении   или

.

Поскольку О – произвольная точка, из найденных разложений вектора  получим:

.

Отсюда следует, что  и, значит,

.                         (2.14)

Покажем, что вектор  коллинеарен вектору , и найдем отношение этих коллинеарных векторов. Имеем:

,

 

 

Откуда . Полученное равенство показывает, что точка  лежит на медиане  и делит ее в отношении 2:1, считая от вершины . □

Примечание. Выдающийся древнегреческий механик и математик Архимед часто в своих геометрических рассуждениях руководствовался соображениями из области механики. Именно таким образом он доказывает теорему о пересечении медиан треугольника.

Представим, что в вершинах треугольника  помещены равные, например, единичные массы. Из механики известно, что если массы из точек  и  перенести в их центр масс, то положение центра масс всей системы, состоящей из масс в точках , , , не изменится. Сумма масс, помещенных в точках  и , равна 2 единицам, а центр масс системы этих двух точек в соответствии с архимедовым правилом рычага находится в середине  отрезка . Поэтому центр масс  всей системы лежит на медиане . Так как в точке  находится масса вдвое большая, чем в , то он будет расположен и вдвое ближе к , чем к . Аналогично установливается, что точка  принадлежит медианам ,  и делит каждую из них в отношении 2:1, считая от вершин.

Из этих рассуждений становится понятным, почему в геометрии точку пересечения медиан треугольника принято называть его центром масс или, короче, – центроидом. Теперь, разумеется, геометрические факты, которые Архимед устанавливал с помощью подобных рассуждений, доказываются математическими средствами. Однако и сегодня знания из области механики могут служить хорошими источниками для выдвижения геометрических гипотез.

В ходе решения задачи 2.6 было доказано, что для любой точки  справедлива формула (2.14), связывающая радиус-вектор центроида  треугольника  с радиусами-векторами его вершин. Оказывается, имеет место и обратное утверждение: если для некоторой точки  и любой точки  имеет место соотношение (2.14), то точка  является центроидом треугольника . Это позволяет сформулировать следующую опорную задачу.

Задача 2.7. Докажите, что точка  является центроидом треугольника  тогда и только тогда, когда

,

где  – произвольная точка.

Решение. Необходимость утверждения доказана, докажем его достаточность. Из равенства (2.14) имеем:

,

где  – середина отрезка . Отсюда  или . Из полученного векторного равенства следует, что точка  делит медиану  треугольника  в отношении 2:1, считая от вершины , и, значит, является центроидом этого треугольника. □

Если в формуле (2.14) в качестве точки  взять точку , то получится еще одно утверждение, часто используемое при решении геометрических задач векторным методом:

Точка  является центроидом треугольника  тогда и

только тогда, когда

.                                (2.15)

Умножая последнее равенство на , получим новую полезную при решении задач векторную формулу:

                              (2.16)

(, ,  – медианы треугольника ).

Возьмем вместо треугольника тетраэдр и воспользуемся рассуждениями Архимеда. Поместим единичные массы в вершинах тетраэдра, тогда масса каждой грани составит 3 единицы, а центр масс грани будет находиться в точке пересечения ее медиан. Отсюда можно заключить, что центр масс всей системы лежит на отрезках, соединяющих вершины тетраэдра с центроидами противоположных граней, и делит их в отношении 3:1, считая от вершин.

Отрезок, соединяющий вершину тетраэдра с центроидом противоположной грани, называют медианой тетраэдра. Поэтому возникшую гипотезу можно сформулировать в виде следующей задачи.

Задача 2.8. Докажите, что медианы тетраэдра пересекаются в одной точке, которая делит каждую из них в отношении 3:1, считая от вершин.

Для доказательства этой гипотезы можно просто трансформировать рассуждения, проведенные для треугольника; мы, однако, поступим иначе – рассмотрим еще один способ рассуждений, который используется при доказательстве и опровержении подобных гипотез.

Решение. Пусть дан тетраэдр . Центроиды граней, противоположных вершинам , , , , обозначим , , ,  соответственно.

Найдем радиус-вектор точки , лежащей на медиане  тетраэдра и делящей ее в отношении 3:1, считая от вершины . Так

как , где  – произвольная точка, и . В силу опорной задачи 4

    .

Следовательно,

.

Выбрав аналогичным образом точки , ,  на медианах ,

,  соответственно и выполнив для них приведенные выкладки, получим:

,

, .

Отсюда следует, что точки , ,  и  совпадают. □

Точка пересечения медиан тетраэдра называется его центром тяжести или центроидом.

Аналогом задачи 2.7 является

Задача 2.9. Докажите, что точка  является центроидом тетраэдра  тогда и только тогда, когда

,                 (2.17)

где  – произвольная точка.

Решение этой опорной задачи представляет собой несложную трансформацию решения задачи 2.6.

Вновь, взяв в (2.17) в качестве точки  точку , приходим к утверждению:

Точка  является центроидом тетраэдра  тогда и только тогда, когда

.                         (2.18)

Умножая это соотношение на , получим формулу

.                        (2.19)

2.3.2. Применение опорных задач и формул. В задачниках по геометрии можно найти большое количество упражнений на доказательство различных векторных соотношений, которые специально рассчитаны на закрепление указанных задач и формул.

Начнем с таких задач.

Пример 2.3.1. Даны два треугольника  и . Докажите, что

,

где ,  – центроиды данных треугольников.

Решение. Пусть  – произвольная точка. Применяя к тре-

       угольникам           

, .

Доказываемое векторное равенство получается в результате вычитания по частям записанных соотношений. □

Пример 2.3.2. Докажите, что центроиды треугольников  и  совпадают тогда и только тогда, когда

.

Решение непосредственно следует из результата предыдущей задачи.

Обобщения данных примеров на случай тетраэдра приведены в задачах для самостоятельного решения. Ясно, что эти задачи решаются аналогично рассмотренным.

Пример 2.3.3. На прямых , , , содержащих стороны треугольника , отмечены точки , ,  соответственно такие, что . Докажите, что центроиды треугольников  и  совпадают.

Решение. Пусть . Тогда в силу формулы (2.11) деления отрезка в данном отношении:

.

Сложим полученные соотношения:

.

Таким образом, имеет место векторное соотношение, доказанное в предыдущем примере, которое является необходимым и достаточным для того, чтобы центроиды треугольников  и  совпадали. □

Пример 2.3.4. Дан параллелепипед . Докажите, что диагональ  параллелепипеда пересекает плоскость треугольника  в его центроиде (рис. 2.22).

Решение. Пусть  – центроид треугольника . Тогда

.

Для решения задачи достаточно показать, что вектор  коллинеа-

                                C_{1                                            D1}                        рен вектору . Найдем

вектор :

 

.

Видим, что . От-

сюда заключаем, что точка  лежит на диагонали  параллелепипеда.

Попутно заметим, что

_{B                             A}       точка  делит эту диаго_{Рис. 2.22}        наль в отношении 1:2, считая от вершины .

Пример 2.3.5. Докажите, что медианы любого треугольника могут служить сторонами некоторого другого треугольника.

Решение. Пусть , ,  – медианы треугольника .

Тогда согласно формуле (2.17) имеет место векторное соотношение

.

Отсюда , при этом векторы  и  не коллинеарны.

От некоторой точки  отложим векторы , и докажем, что треугольник  является искомым. Из определения разности векторов и выполненных построений следует, что . Поэтому в треугольнике   

. □

Примечание. Приведенные примеры показывают, что при решении геометрических задач векторным методом часто удается избежать громоздких чертежей. Иногда чертежи бывают и вовсе не нужны. Следует помнить, что среди учебных задач на векторный метод встречается немало задач, которые специально направлены на отработку той или иной формулы. К таким задачам относится, например, следующая:

Точки  и  являются центроидами тетраэдров  и .

Докажите, что .

Часто можно наблюдать такую типичную ситуацию. Решающий старательно и утомительно долго выполняет к этой задаче чертеж. Когда чертеж готов, наступает разочарование: чертеж не только не проясняет ситуацию, а, наоборот, делает ее еще более запутанной. Для решения задачи чертеж вовсе не требуется; она составлена как учебная задача на усвоение векторной формулы , связывающей центроид и вершины тетраэдра.

 

Задачи для самостоятельного решения

 

45.               Докажите, что существует треугольник, стороны которого равны и параллельны медианам данного треугольника.

46.               Соответственные медианы треугольников  и  

параллельны. Докажите, что соответственные стороны этих треугольников также параллельны.

47.               Докажите, что если медианы одного треугольника параллельны сторонам другого треугольника, то медианы второго параллельны сторонам первого.

48.               Внутри треугольника  взята произвольная точка ; ,

, , – центроиды треугольников , ,  соответственно. Найдите площадь треугольника , если площадь треугольника  равна . Изменится ли найденный результат, если точка  лежит вне треугольника?

49.               Стороны треугольника  равны медианам , ,  треугольника . Найдите отношение площади треугольника  к площади треугольника .

50.               Докажите, что существует пространственный четырехугольник, стороны которого равны и параллельны медианам данного тетраэдра.

51.                – произвольный четырехугольник; , , ,  – центроиды треугольников , , , . Докажите, что четырехугольник  подобен четырехугольнику .

52.               Докажите, что центроиды граней тетраэдра являются вершинами тетраэдра, гомотетичного данному.

53.               Точки , ,  делят стороны , ,  треугольника  в одном и том же отношении:

.

Докажите, что центроиды треугольников  и  совпадают.

54.               Вершины , ,  треугольника  принадлежат соответственно сторонам , ,  треугольника , а центроиды этих треугольников совпадают. Докажите, что точки , ,  делят стороны треугольника  в равных отношениях.

55.               Докажите, что вершина  четырехугольника , точка  пересечения его средних линий и центроид  треугольника  

лежат на одной прямой, причем .

56.               Даны два тетраэдра  и . Докажите, что

,

где ,  – центроиды данных тетраэдров.

57.               Даны два тетраэдра  и . Докажите, что цен-

троиды этих тетраэдров совпадают тогда и только тогда, когда

.

58.               Докажите, что бимедианы тетраэдра (отрезки, соединяющие середины скрещивающихся ребер) пересекаются в его центроиде.

 

§ 2.4. Теоремы инцидентности

 

Точка и прямая (плоскость) называются инцидентными, если точка лежит на прямой (плоскости); прямая и плоскость называются инцидентными, если прямая лежит в плоскости.

 

2.4.1. Теоремы Менелая и Чевы и их стереометрические аналоги. Рассмотрим векторное доказательство теоремы, открытие которой приписывается древнегреческому геометру и астроному Менелаю Александрийскому (I-II в.н.э.). Эта теорема позволяет устанавливать инцидентность (принадлежность) трех точек одной прямой.

Задача 2.10 (теорема Менелая). На прямых , , , содержащих стороны треугольника , взяты точки , ,  соответственно, не совпадающие с вершинами треугольника (рис. 2.23). Докажите, что точки , ,  лежат на одной прямой тогда и только тогда, когда

.                 (2.11)

Решение. Точки , ,  лежат на одной прямой тогда и только тогда, когда векторы коллинеарны, т. е.

.

Пусть , , , тогда условие

(2.11), которое требуется доказать, примет вид . По определению отношения трех точек            ,

      .      Тогда      

 и по формуле деле-

ния отрезка в данном отношении . Откуда

      .     Учитывая,

что, равенство  можно переписать в

виде  или

.

             Векторы          и  не коллинеарны, поэтому

                          , .

Отсюда  и, следовательно, необходимое и достаточное условие принадлежности точек , ,  одной прямой действительно принимает вид . □

Теорема, в некотором смысле сходная с теоремой Менелая, позволяет установить, проходят ли три прямые через одну точку. Открытие этой теоремы принадлежит итальянскому инженеругидравлику и геометру Чеве Джованни, а ее доказательство опубликовано им в 1678 году. Рассмотрим векторное доказательство этой теоремы.

Задача 2.11 (теорема Чевы). На прямых , , , содержащих стороны треугольника , даны точки , ,  соответственно. Докажите, что прямые , ,  пересека-

ются в одной точке или параллельны тогда и только тогда, когда

.                 (2.12)

Решение. Пусть прямые , ,  пересекаются в точке  (рис. 2.24). Применяя теорему Менелая к треугольнику  и прямой , а затем к треугольнику  и прямой , приходим к соотношениям

,                    (2.13)

         A                          B₁                      C        A                    B₁                     C

                            Рис. 2.24                                            Рис. 2.25

.                    (2.14)

Обозначим , тогда ,

. Из первого равенства . Второе

равенство сначала перепишем в виде       ; отсюда  и . Затем преобразуем его следующим       образом: .         Отсюда

.

С учетом проведенных вычислений соотношения (2.13), (2.14) перепишутся в виде

 

Перемножая по частям найденные соотношения, получим

.

Если прямые , ,  параллельны (рис. 2.25), то . Введем            обозначения:

; тогда , . Отсюда

заключаем, что , т.е. . Соотношение

(2.12) выполняется.

Обратно, пусть выполнено равенство (2.12). Рассмотрим прямые , ; будем считать, что они пересекаются в некоторой точке . Проведем прямую , точку пересечения этой прямой с прямой  обозначим . По доказанному

.

Отсюда и (2.12) заключаем, что , где  –

. Но тогда

,  и  или

. Так как , то последнее равенство возможно лишь при условии , т. е. когда точки  и  совпадают. Следовательно, все три прямые ,  и  пересекаются в точке .

В том случае, когда , аналогично доказывается, что

. □

Прямые, проходящие через вершины треугольника и пересекающиеся в одной точке называются чевианами этой точки.

Очевидно, что теорема Архимеда о пересечении медиан треугольника является следствием теоремы Чевы. Действительно, если точки , ,  будут серединами сторон , ,  треугольника

, то  и, значит, условие теоремы Чевы выполняется.

При решении некоторых задач на инцидентность соотношения Менелая (2.11) и Чевы (2.12) удобней использовать в так называемой угловой или тригонометрической форме. Для получения этих соотношений введем на плоскости ориентацию углов.

Угол будем называть направленным (ориентированным), если его стороны заданы в определенном порядке. Пусть  и у него первой задана сторона , а второй – сторона . Если для совмещения стороны  со стороной  ее нужно повернуть вокруг точки  против часовой стрелки, то угол  условимся считать положительным и имеющим величину , если – по часовой стрелке, – отрицательным и имеющим величину . При этом величину развернутого угла удобно считать равной , тогда любой направленный угол будет иметь величину . На чертеже ориентированный угол будем отмечать дугой со стрелкой, направленной от первой стороны угла ко второй.

Пусть точка  делит отрезок  в отношении , считая от точки , и точка  не принадлежит прямой .

В треугольнике  по теореме синусов , а в

треугольнике  Откуда

 

Если точка  делит отрезок  внутренним образом, то углы  и  являются смежными (рис. 26, а), а значит,

. Углы же  и  

ориентированы одинаково, поэтому .

                                      D                                                            D

             A                          C               B              A                             B              C

Рис. 2.26

Если точка  делит отрезок  внешним образом (рис. 26, б), то . Так как теперь углы  и  имеют

противоположную ориентацию, то и в этом случае

.                           (2.15)

Перепишем соотношения Менелая и Чевы используя найденную формулу (2.15) для вычисления отношения трех точек прямой.

, .

С учетом введенных обозначений (рис. 2.27) соотношение Менелая (2.11) перепишется в виде

 

или

 

A                                           C           B₁                 A                                         C           B₁

                             _{Рис. 2.}27                                                         Рис. 2.28

Аналогично получаем тригонометрическую форму соотношения

Чевы (рис. 2.28).

 

Рассмотренные теоремы имеют пространственные аналоги.

Сформулируем и докажем теперь стереометрический аналог теоремы Менелая. Для этого вместо треугольника рассмотрим пространственный четырехугольник и найдем условие, при выполнении которого точки, принадлежащие прямым, содержащим стороны этого четырехугольника, и отличные от его вершин, лежат в одной плоскости.

Задача 2.12. На прямых , , , , содержащих стороны неплоского четырехугольника , взяты точки , , ,  соответственно, не совпадающие с вершинами четырехугольника (рис. 2.29). Докажите, что точки , , ,  принадлежат одной плоскости тогда и только тогда, когда

.              (2.16)

                Решение.                Пусть , , ,

, тогда . По аналогии с решением предыдущей задачи выпишем векторы  

. Откуда .

Точки , , ,  принадлежат одной плоскости тогда и только тогда, когда векторы , ,  компланарны. Учитывая разложения этих векторов по векторам ,  и , условие их компланарности удобно записать в виде:  

. После подстановки

в записанное равенство разложений векторов ,  и  получим:

.

       Так как векторы      ,  и       не компланарны, то

                                          ,  ,  .

Отсюда ,  и необходимое и достаточное условие принадлежности точек , , ,  одной плоскости принимает вид

. □

Пусть для точек , , , , лежащих на прямых, содержащих стороны пространственного четырехугольника , выполнено условие (2.16) и  – точка пересечения прямых  и  

(рис. 2.29). Прямая  является линией пересечения плоскостей  и , прямая  – плоскостей  и , при этом все четыре плоскости проходят через точку . Поэтому стереометрический аналог теоремы Чевы можно сформулировать следующим образом:

Пусть на прямых , , , , содержащих стороны неплоского четырехугольника , взяты точки , , ,  соответственно, не совпадающие с вершинами четырехугольника. Тогда (2.15) – необходимое и достаточное условие того, что плоскости , , ,  пересекаются в одной точке.

Примечание. В книге [18] можно также найти обобщения необходи-

мых условий теорем Менелая и Чевы на случай плоских -угольников при .

Если прямая пересекает стороны , , …, ,  плоского многоугольника  в точках , , … ,  соответственно, то

,

где знак «+» соответствует случаю четного , знак «–» – случаю нечетного .

Пусть точка  лежит в плоскости многоугольника  с нечетным числом сторон. Если прямые , ,…, , …,  пересекают противоположные вершинам , , … , , …  стороны многоугольника в точках , , …, , , …,  

соответственно, то

.

2.4.2. Применения опорных теорем. Теоремы, рассмотренные в предыдущем пункте, широко используются при доказательстве других теорем об инцидентности точек и прямых (плоскостей). В качестве примеров приведем доказательства еще трех именных теорем, опирающиеся на теорему Менелая.

Пример 2.4.1 (теорема Паппа^). На одной прямой взяты точки , , , а на другой – точки , , . Прямые  и

,  и ,  и  пересекаются в точках ,  и  соответственно, а прямые ,  и  попарно пересекаются в точках, не лежащих на одной прямой (рис. 2.30). Докажите, что точки , ,  лежат на одной прямой.

Решение. Рассмотрим вспомогательный треугольник , стороны которого расположены на прямых ,  и . Принадлежащие одной прямой точки , ,  лежат на сторонах этого треугольника, поэтому по теореме Менелая

.

Аналогичные равенства имеют место для троек точек , ,  и

       , , :                                                                                 _B

,  ,

а также для троек точек , ,  и , , :

               , .

Учитывая последние два равенства, после перемножения первых трех получим:

.

                  Следовательно, по теореме Ме-         ¹                       B1                   C₁

нелая точки , ,  лежат на од-

       ной прямой. □                                                         Рис. 2.30

Пример 2.4.2 (теорема Дезарга^). Докажите, что если треугольники  и  расположены так, что прямые ,

,  пересекаются в одной точке или параллельны, то либо три точки пересечения соответственных сторон треугольников  и  лежат на одной прямой, либо две соответствен-

ные стороны параллельны между собой и параллельны прямой, проходящей через точки пересечения других пар соответственных

                                                   

^ Папп Александрийский – древнегреческий математик, творчество которого приходится на вторую половину 3 в.н.э.

^ Дезарг Ж. (1593-1602) – французский математик и архитектор; стоял у истоков возникновения проективной геометрии.

сторон, либо каждые две соответственные стороны параллельны между собой. 

Решение. Начнем со случая, когда прямые , ,  пересекаются в одной точке. Пусть , ,  – точки пересечения прямых  и ,  и ,  и  соответственно

(рис. 2.31). 

Последовательно применяя теорему Менелая к треугольнику  и прямой , треугольнику  и прямой , треугольнику  и прямой , запишем равенства:

,

, .

Перемножив эти равенства и учитывая, что

,

получим:

.

Но точки , ,  принадлежат прямым, содержащим стороны треугольника , поэтому по теореме Менелая они лежат на одной прямой.

Пусть теперь прямые  и  пересекаются в точке , прямые  и  – в точке , а прямые  и  параллельны (рис. 2.32, а).

          В    этом     случае ,

. Разложим вектор  по векторам , :

 

Положим с одной стороны,

        

.

С другой стороны,

 

 .

Сравнивая разложения вектора  по неколлинеарным векторам

, приходим к системе из кото-

рой следует, что . Следовательно,

.

Аналогично находим вектор

.

Поэтому

Таким образом, вектор  коллинеарен вектору  и, значит, параллельные стороны ,  треугольников  и

 параллельны прямой, проходящей через точки пересечения других пар соответственных сторон.

                                                   ^C2                                     Рис. 2.32

Если же каждые две соответственные стороны треугольников  и  параллельны между собой, то эти треугольники гомотетичны в гомотетии с центром  (рис. 2.32, б).

Перейдем к случаю, когда прямые , ,  параллельны между собой.

Пусть прямые  и  пересекаются в точке ,  и

 – в точке . Точку пересечения прямой  с прямой  обозначим , а точку ее пересечения с прямой  – буквой . Докажем, что точки  и  совпадают.

Для этого применим теорему Менелая сначала к треугольнику  и прямой , а затем к треугольнику  и прямой

:

, .

Так как прямые ,  пересечены параллельными прямыми

, , а прямые ,  – параллельными прямыми ,

, то ,  (задача

2.4). Поэтому из выписанных соотношений вытекает равенство

, из которого следует, что точки  и  делят

отрезок  в одном и том же отношении, и, следовательно совпадают (рис. 2.33).

На рисунках 2.34 представлены ситуации, когда две (каждые две) соответственные стороны треугольников параллельны между собой. Рассмотрите эти случаи самостоятельно. □

Доказанная теорема Дезарга имеет обратную (см. задачу 70 для самостоятельного решения).

Рис. 2.34

Пример 2.4.3 (теорема Гаусса^[3]). Докажите, что если никакие стороны четырехугольника не параллельны, то середина отрезка, соединяющего точки пересечения противоположных сторон, лежит на прямой, соединяющей середины диагоналей.

Решение. Пусть ,  – середины диагоналей ,  четырехугольника ,  – середина отрезка , где ,  – точки пересечения противоположных сторон  и ,  и  этого четырехугольника (рис. 2.35).

Если через точку  провести прямую, параллельную прямой , то она по теореме Фалеса пересечет отрезки ,  в их серединах  и  со-

ответственно.         Рассмотрим треугольник , образованный средними линиями треугольника . Очевидно, что точки , ,  лежат на

прямых, содержащих стороны треугольника . Поэтому для доказательства теоремы Гаусса достаточно установить, что для этих точек и треугольника  выполнено условие теоремы Менелая. 

Применяя теорему Менелая к треугольнику  и точкам ,

, , имеем равенство

.

Согласно задаче 2.5

, , .

Поэтому, перемножая по частям три последних равенства, получим

.

Таким образом, точки ,  и  лежит на одной прямой. Эту прямую называют прямой Гаусса. □

Теорема Менелая позволяет значительно упростить решение многих задач на вычисление отношений пропорциональных отрезков.

Пример 2.4.4. На сторонах  и  треугольника  даны точки  и  соответственно, такие, что . В каком отношении точка  пересечения отрезков  и  делит каждый из этих отрезков?

Решение. Применим теорему Менелая к треугольнику  и точкам , ,  прямой , лежащим на сторонах этого треугольника (рис. 2.36):

.

Из условий задачи следует, что

C , . Поэтому  и, значит,

. 

Применяя теорему Менелая к треугольнику  и точкам ,

                                                                          , ,       аналогично    получим:

     A                         K                        B          . От-

                             Рис. 2.36                          сюда  и, следователь-

но, . □

Так же точно при решении соответствующих стереометрических задач используется пространственный аналог теоремы Менелая.

Пример 2.4.5. На ребрах , ,  тетраэдра  взяты соответственно точки , ,  так, что ,  

, . Найдите отношение объемов частей, на которые плоскость  делит тетраэдр.

Решение. Обозначим через  точ-

D                     ку пересечения плоскости  с ребром  (рис. 2.37). Применяя к пространственному       четырехугольнику  и точкам , ,  стереометрический аналог теоремы Менелая, най-

^A                                                          дем отношение, в котором точка  де-

                                                            лит ребро      . Соотношение

 

                      Рис. 2.37                     принимает      вид .

Откуда , т. е. .

Будем считать, что , , ,  – высота тетраэдра , опущенная из вершины , а  – его высота, опущенная из вершины . Тогда

.

Найдем объем многогранника . Для этого разобьем его на три треугольные пирамиды ,  и .

Высота пирамид , , опущенная из общей вершины

, равна ,

 

Поэтому

, .

Аналогично находим высоту  пирамиды , опущенную из вершины , и площадь грани :

.

Следовательно, .

Суммируя найденные объемы, получим:

 

Таким образом, отношение объемов частей, на которое плоскость  делит тетраэдр, равно . □

Прежде чем перейти к примерам использования теоремы Чевы, докажем следующее свойство чевиан треугольника.

Пример 2.4.6 (теорема Ван-Обеля^[4]). На прямых , , , содержащих стороны треугольника , заданы соответственно точки , ,  так, что прямые , ,  пересекаются в точке . Докажите, что

.

Решение. Рассмотрим случай, когда точка  пересечения чевиан лежит внутри треугольника. Через вершину  треугольника  проведем прямую, параллельную стороне . Точки пересечения этой прямой с прямыми ,  обозначим соответственно  и  

(рис. 2.38, а).

Треугольник  будет подобен треугольнику . Поэтому

.

Из подобных треугольников  и ,  и  соответственно находим:

.

Следовательно,  или

.

Когда точка  пересечения чевиан лежит вне ка, доказательство выполняется аналогично (рис. 2.38, б). Здесь треугольник  подобен треугольнику , треугольник

 – треугольнику , а треугольник  – треугольнику

. Откуда следует, что

,

и, следовательно, . Остается учесть, что теперь точки , ,  делят отрезки , ,  соответственно внешним образом.

Очевидно, что доказанная теорема справедлива для каждой из чевиан, т. е.

,

. □

Пример 2.4.7. Докажите, что

а) биссектрисы треугольника пересекаются в одной точке;

б) высоты треугольника пересекаются в одной точке;

в) прямые, соединяющие вершины треугольника с точками касания противоположных сторон вписанной в треугольник окружности, пересекаются в одной точке.

Решение. а) Пусть , ,  – биссектрисы внутренних углов треугольника  (рис. 2.39); , ,  – длины сторон ,  и  соответственно. По свойству биссектрис треугольника

,

Чевы прямые , ,  пересекаются в одной

точке.

б) Пусть , ,  – высоты треугольника  (рис. 2.40, а, б). Из подобия треугольников  и ,  и ,  и  соответственно имеем:

.

                     а)                          A                       б)

A1

C1

Рис. 2.40

Отсюда следует, что

.

Если треугольник  остроугольный, то основания высот , ,  делят его стороны внутренним образом (рис. 2.40, а). В этом случае  и, следовательно,

.

Если треугольник  тупоугольный, то основание одной из высот делит сторону треугольника внутренним образом, а основания двух других высот – внешним. Так на рисунке 2.40, б точка  делит отрезок  внутренним образом, а точки  и , делят отрезки  и  внешним образом. Поэтому в этом случае ,  и также .

Таким образом, прямые, содержащие высоты , ,  треугольника, пересекаются в одной точке.

в) Пусть , ,  – прямые, соединяющие вершины треугольника  с точками касания противоположных сторон вписанной в треугольник окружности (рис. 2.41).

По свойству касательной к окружности ,

, . По-

этому

    

                                                                              Следовательно,    по    теореме

C                   A₁                                                              B           Чевы прямые , ,  

                  Рис. 2.41                                    пересекаются в одной точке. □

 

Пример 2.4.8. На сторонах треугольника вне его построены квадраты. Докажите, что прямые, проходящие через вершины треугольника и центры квадратов, построенных на противоположных сторонах, пересекаются в одной точке.

Решение. Пусть  – данный треугольник. Центры квадратов, построенных на сторонах треугольника, противолежащих вершинам , , , обозначим ,,  соответственно (рис. 2.42).

Используем для доказательства теорему Чевы в тригонометрической форме.

Из треугольников  и  по теореме синусов будем иметь:

.

Учитывая, что , отсюда находим:

 

Аналогичные пропорции получим           из         треугольников

,  и из треугольников , :

 

 

Перемножая по частям найденные равенства, прихо- Рис. 2.42

дим к соотношению

 

Таким образом, условие Чевы выполняется. Следовательно, прямые ,  и  пересекаются в одной точке. □

 

Задачи для самостоятельного решения

 

59.              Найдите отношение, в котором прямая, проходящая через вершину  и середину медианы  треугольника , делит его сторону .

60.              Решите задачу 33 используя теорему Менелая.

61.              Через точки  и , лежащие вне окружности, проведены касательные  и  к этой окружности. Найдите отношение, в котором прямая , проходящая через точки касания, делит отрезок .

62.              Примените теорему Менелая к решению задачи, рассмотренной в примере 2.2.6.

63.              Прямая пересекает прямые , , , содержащие стороны треугольника , в точках , ,  соответственно. Точки

, ,  симметричны точкам , ,  относительно середин сторон , , . Докажите, что точки , ,  лежат на одной прямой.

64.              Противоположные стороны вписанного в окружность шестиугольника не параллельны. Докажите, что точки пересечения прямых, содержащих эти стороны, лежат на одной прямой (теорема Паскаля^1).

65.              Докажите, что точки пересечения прямых, содержащих стороны неравнобедренного треугольника, с касательными к описанной около него окружности в противоположных вершинах треугольника лежат на одной прямой.

66.              Четырехугольник , противоположные стороны которого не параллельны, вписан в окружность. Докажите, что:

а) точки пересечения прямых, содержащих противоположные стороны четырехугольника, и точки пересечения касательных к окружности в его противоположных вершинах лежат на одной прямой;

б) точка пересечения прямых  и , точка пересечения

прямой  с касательной к окружности в точке  и точка пересечения прямой  с касательной в точке  лежат на одной прямой.

67.              Докажите, что ортогональные проекции точки на прямые, содержащие стороны треугольника, лежат на одной прямой тогда и только тогда, когда эта точка лежит на окружности, описанной около треугольника. (Прямая, на которой лежат проекции, называется прямой Симсона^ точки окружности, описанной около треугольника.)

68.              Используя теорему Чевы, докажите, что

а) прямые, проходящие через вершины треугольника и деля-

щие его периметр пополам, пересекаются в одной точке;

б) прямые, соединяющие вершины треугольника с точками касания противоположных сторон с соответствующими вневписанными окружностями, пересекаются в одной точке.

69.              Докажите, что в шестиугольнике, описанном около окружности, прямые, проходящие через противоположные вершины, пересекаются в одной точке (теорема Брианшона^).

70.              На одной прямой взяты точки , , , а на другой – точки , , , при этом прямая  параллельна прямой , а

                                                   

^ Паскаль Б. (1623-1662) – выдающийся французский математик, физик и философ.

^ Симсон Р. (1687-1768) – шотландский математик.

^ Брианшон Ш.Ж. (1785-1864) – французский математик.

прямая  – прямой . Докажите, что прямые  и  также параллельны.

71.              Сформулируйте и докажите теорему, обратную теореме Дезарга.

72.              Плоскость, проходящая через середины  и  ребер  и  тетраэдра , пересекает ребро  в точке , а ребро  – в точке . Докажите, что .

73.              На ребрах , ,  тетраэдра  взяты соответственно точки , ,  такие, что . Найдите отношения, в которых плоскость  делит прямые, содержащие остальные ребра этого тетраэдра.

74.              Плоскость пересекает ребра , ,  тетраэдра  в точках , ,  так, что .

Найдите объем тетраэдра , если объем тетраэдра  равен .

75.              На ребрах  взяты соответственно точки , ,  такие, что . Найдите отношение объемов многогранников, на которые плоскость  делит тетраэдр .

76.              Стороны , , ,  пространственного четырехугольника  касаются сферы в точках , , ,  соответственно. Докажите, что точки касания лежат в одной плоскости.

77.              Используя теорему Ван-Обеля, найдите отношения, в которых делятся биссектрисы внутренних углов треугольника точкой их пересечения.

78.              Точка  – точка пересечения чевиан , ,  треугольника . Докажите, что

 . 

        

Глава III

 

МЕТРИЧЕСКИЕ ЗАДАЧИ

 

Для решения аффинных задач векторным методом, как мы видели, достаточно двух основных операций: сложения векторов и умножения вектора на число. Кроме того, используется операция вычитания векторов, обратная для операции сложения. Результатом выполнения этих трех операций является новый вектор. В метрических задачах ищутся длины, величины углов, площади, объемы. Для того чтобы использовать векторный метод при решении метрических задач, требуются операции, которые ставят в соответствие векторам не векторы, а числа. Одной из таких операцией является скалярное произведение векторов; эта операция ставит в соответствие паре векторов действительное число.

В учебниках геометрии векторы появляются достаточно поздно, когда состоялось знакомство с большим числом важнейших метрических понятий и фактов. При решении задач с помощью векторов неразумно отказываться от уже приобретенных знаний или всякий раз стремиться получить их заново в векторной форме. Поэтому будем опираться на такие фундаментальные факты метрической геометрии, как теоремы синусов, косинусов и др., которые были ранее доказаны без использования векторов. При решении метрических задач векторным методом важно опять научится представлять и затем применять известные геометрические факты в векторной форме. Например, теорему косинусов  для треугольника  со сторонами , ,  на основании определения ска-

лярного произведения векторов можно записывать и использовать в виде  и т. п.

В данной главе приведены примеры более простых «векторных доказательств» некоторых метрических теорем школьного курса геометрии и продемонстрирована универсальность векторного метода при решении определенных классов задач. Вместе с тем, не следует делать доказательство теорем и поиск решений геометрических задач векторным методом самоцелью. Существуют теоремы, которые, наоборот, более естественно, просто и красиво доказываются геометрическими и обычными алгебраическими методами; то же самое можно сказать и в отношении методов решения задач.

 

§ 3.1. Задачи на доказательство и вычисление

 

3.1.1. Основные опорные формулы и приемы. Пара точек ,  определяет отрезок ; метрической величиной, характеризующей отрезок, является длина отрезка. Если точки ,  различные, то длина отрезка  принимается за расстояние  между точками  и ; если точки  и  совпадают, то по определению принимают: . Из формулы (1.12) для вычисления длины вектора непосредственно следует:

                            (3.1)

Три точки ,  и , не лежащие на одной прямой, определяют три угла и треугольник , для которого они являются вершинами. Метрической величиной, характеризующей угол, является величина или мера угла. Величину угла, например , можно найти из формулы (1.13):

.                     (3.2)

Основными метрическими величинами, характеризующими треугольник , являются длины его сторон, меры углов и площадь . Векторное выражение формулы для вычисления площади треугольника можно получить следующим образом:

 

Таким образом,

                (3.3)

Четыре точки , ,  и , не лежащие в одной плоскости, определяют тетраэдр , для которого они являются вершинами. Наряду с линейными и угловыми элементами, площадями граней тетраэдр характеризует новая метрическая величина – объем. Объем тетраэдра  можно найти по формуле , где  – высота тетраэдра, опущенная из вершины  на плоскость грани . Площадь грани  тетраэдра можно вычислить с помощью формулы (3.3), найдем его высоту . Для этого используется следующий стандартный прием.     Рассмотрим     вектор

(рис. 3.1). Век-

тор  представим в виде линейной комбинации неколлинеарных векторов , тогда

.

Скалярно умножая это равен-

ство сначала на вектор , а затем на вектор , и учитывая, что

 

                       (3.4)

из которой можно найти  и . Высота тетраэдра

                                               .

Этот же прием, как будет показано ниже, используется при вычислении расстояний от точки до плоскости и между скрещивающимися прямыми.

При решении метрических задач векторным методом достаточно часто приходится пользоваться известными из школьного курса геометрии векторными тождествами

, ,

,

имеющими место для любых двух векторов  и . В стереометрических задачах нередко используется обобщение первого из этих тождеств:

,

справедливое для любых векторов ,  и .

Кроме того, в задачах на доказательство геометрических неравенств применяется векторная форма записи неравенства треугольника

.

(Равенство  имеет место тогда и только тогда,

когда векторы  и  коллинеарны.)

Еще два полезных тождества, которые рекомендуется запомнить и «взять на вооружение», доказываются в следующей задаче.

Задача 3.1. Докажите, что для любых четырех точек , ,  и  имеет место тождество:

а)

б) .

Решение. а) При доказательстве тождества снова применяется стандартный прием: все входящие в выражение векторы заменяются векторами, отложенными от одной точки. Используя определение разности, векторы , , ,  заменим векторами, отложенными от точки . Тогда левую часть тождества можно преобразовать следующим образом:

 .

Скалярное произведение векторов коммутативно, поэтому найденное выражение равно нулю.

б) При доказательстве тождества используется формула разности скалярных квадратов векторов. С помощью этой формулы левую часть тождества можно преобразовать так:

. □

Вычисление расстояний. Пусть даны прямая  и не лежа-      ^M щая на ней точка . Расстояние  от точки  до прямой  равно длине перпендикуляра

_{, опущенного из данной точки} A B на данную прямую (рис. 3.2).  ^{Рис. 3.2}

Длина этого перпендикуляра

равна высоте  треугольника  поэтому

,

где  можно найти по формуле (3.3). С учетом этой формулы

.                      (3.5)

Полученная         формула         позволяет        вычислять       расстояние  между параллельными прямыми  и . Все точки одной из параллельных прямых расположены на одинаковом расстоянии от другой прямой. Поэтому искомое расстояние можно найти как расстояние от любой точки, например , прямой  до прямой .

Расстояние  от данной точки  до данной плоскости  находится как длина высоты тетраэдра , опущенной из вершины  на плоскость основания . Аналогично вычисляется расстояние между параллельными плоскостями и между прямой и плоскостью, которой она параллельна.

Расстоянием между скрещивающимися прямыми является длина их общего перпендикуляра, где под общим перпендикуляром понимается отрезок с концами на данных прямых, который перпендикулярен каждой из них. Та-

D                      кой перпендикуляр, как доказано в          курсе   геометрии,      является единственным.

Пусть даны скрещивающиеся прямые  и  (рис. 3.3). Если через каждую из них провести плоскость, параллельную другой прямой, то длину общего перпендикуляра прямых  и  можно

Рис. 3.3                      найти как расстояние между построенными        параллельными

плоскостями. Отложим от точки  вектор , равный вектору . Точка  лежит в плоскости, проходящей через прямую  параллельно прямой , поэтому 

                             (3.6)

Вычисление углов. Рассмотрим, как с помощью векторов найти углы между двумя прямыми, прямой и плоскостью, двумя плоскостями.

Угол между двумя прямыми. Пусть требуется найти угол  между прямыми  и . Если прямые параллельны,

то угол между ними считается равным . Если прямые пересекаются, то они образуют четыре угла. В том случае, когда все четыре угла равны между собой, прямые называются перпендикулярными, а угол между ними равен  (рис. 3.4, а). Если пересекающиеся прямые не перпендикулярны, то они образуют две пары равных углов, два острых и два тупых. В этом случае за угол  между прямыми принимают величину острого угла, образованного этими прямыми (рис. 3.4, б). Угол между скрещивающимися прямыми определяется как угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым (рис. 3.4, в). Таким образом, угол  между прямыми лежит в пределах , косинус такого угла принимает неотрицательные значения.

 

С помощью скалярного произведения можно найти косинус угла между направляющими векторами  и  данных прямых  и

. Угол  между векторами  и  может принимать значения в промежутке от  до . Если , то угол  равен углу  между прямыми  и  (рис. 3.5, а). В том случае, когда

, угол  между прямыми  и  равен разности

 (рис. 3.5, б). Учитывая, что  

, для вычисления косинуса угла  между прямыми  

и  можно использовать формулу:

.                                       (3.7)

                                       б)

Рис. 3.5

Угол между прямой и плоскостью. Для вычисления с помощью векторов углов между прямыми и плоскостями и углов между плоскостями вводится нормальный вектор плоскости. Вектор  называется нормальным вектором плоскости , если он ортогонален всем векторам, лежащим в плоскости  и ей параллельным.

Если прямая параллельна плоскости, то угол между ними считается равным . Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости; в этом случае угол между прямой и плоскостью равен

. Если прямая не перпендикулярна плоскости, то углом между ними называется угол между этой прямой и ее ортогональной проекцией на плоскость.

          a            б)

Рис. 3.4

При вычислении угла  между прямой  и плоскостью  используются направляющий вектор  прямой  и нормальный вектор  плоскости . Если угол  острый, то

(рис. 3.4, а); если угол  тупой,

то (рис. 3.4, б).

Поэтому синус искомого угла вычисляется по формуле:

.                                      (3.8)

Угол между двумя плоскостями. Если данные плоскости  и  параллельны, то угол между ними считается равным . Если

плоскости пересекаются, то они образуют четыре двугранных угла с общим ребром. Двугранный угол измеряется своим линейным углом. В том случае, когда все четыре двугранных угла прямые, плоскости  и  называются перпендикулярными, а угол между ними равен  . Если плоскости не перпендикулярны, то они образуют две пары равных двугранных углов. В этом случае за угол между плоскостями принимают величину тех двугранных углов, которая меньше . Таким образом, угол между двумя плоскостями может лежать в промежутке от  до .

Вычисление угла  между плоскостями сводится к вычислению угла между нормальными векторами  и  этих плоскостей. Действительно, если , то угол  равен углу  между плоскостями  и  (рис. 3.5, а). В том случае, когда

, угол (рис. 3.5, б). В силу то-

го, что , для вычисления косинуса угла  между плоскостями  и  получим формулу:

.                                     (3.9)

Во все приведенные опорные формулы входит скалярное произведение векторов. Как было отмечено во введении, в школьных учебниках геометрии имеются только формулы для вычисления скалярного произведения векторов, заданных своими координатами в ортонормированных базисах. Часто, однако, гораздо удобней уметь вычислять его в произвольных, а не в ортонормированных базисах. Рассмотрим, какая для этого требуется дополнительная информация о базисных векторах.

Пусть на плоскости задан базис , образованный неколлинеарными векторами , , а векторы  и  заданы своими координатами в этом базисе:

, .

Тогда на основании свойств скалярного произведения векторов

Таким образом, для того чтобы найти скалярное произведение  векторов  и , заданных своими координатами в базисе , необходимо знать скалярные квадраты ,  базисных векторов и их скалярное произведение . Поскольку

,

то отсюда следует, что для вычисления скалярного произведения в базисе  нужно знать длины  базисных векторов и угол  между ними.

Скалярное произведение векторов пространства, заданных своими координатами в базисе, образованном упорядоченной тройкой некомпланарных векторов, вычисляется аналогично. Пусть векторы  и  заданы своими координатами в базисе

:

, .

Тогда

 .

Следовательно, для вычисления скалярного произведения в ба-

зисе  нужно знать длины , ,  базисных векторов и углы между ними.

При проведении вычислений в задачах с конкретными числовыми данными для скалярных произведений базисных векторов удобно предварительно составить таблицу, в первом столбце и верхней строке которой стоят перемножаемые векторы, в клетке на пересечении строки и столбца – скалярное произведение соответствующих векторов.

 

В этой таблице , , .

Прежде чем перейти к рассмотрению примеров решения метрических задач векторным методом, сделаем следующее замечание. Неоспоримым достоинством выбора векторного метода при их решении является возможность легко и быстро «увидеть» план решения, т. е. выделить последовательность опорных подзадач, которые необходимо решить для ответа на вопрос или требование задачи. Однако надо быть готовым к тому, что реализация найденного плана решения нередко превращается в малоинтересное и весьма трудоемкое занятие.

3.1.2. Задачи на доказательство. Векторным методом можно решить значительную часть задач из школьных учебников и задачников по геометрии, он может быть использован при решении отдельных геометрических задач, предлагаемых на итоговых государственных испытаниях по математике. В пособии рассмотрены только задачи на доказательство и вычисление, поскольку именно эти задачи могут встретиться на экзамене. Вместе с тем, этот метод может с успехом применяться при решении задач на максимум и минимум, отыскание геометрических мест точек, доказательство геометрических неравенств.

Пример 3.1.1. Докажите, что диагонали четырехугольника перпендикулярны тогда и только тогда, когда суммы квадратов его противоположных сторон равны.

Решение. Пусть диагонали ,  четырехугольника  перпендикулярны, тогда . Из второго тождества задачи

1 следует, что в этом случае . Откуда  или .

Проведя преобразования в обратном порядке, получим:

. Отсюда следует, что диагонали четырехугольника  перпендикулярны. □

Пример 3.1.2. Точка  является серединой основания  равнобедренного треугольника , отрезок  перпендикулярен стороне  (), точка  – середина отрезка . Докажите, что отрезки  и  перпендикулярны.

Решение. Примем векторы ,  за базисные и положим  (треугольник  равнобедренный). Тогда из условий задачи следует, что . Отсюда

, .

Векторы  и  ортогональны, поэтому

 

A                           D                   B                 ^,

                           Рис. 3.6                    и, следовательно,

.

Точка

.

Найдем скалярное произведение векторов      и :

.

Учитывая, что , получим

          

Таким образом, векторы  и  ортогональны, а значит, отрезки  и  перпендикулярны. □

Пример 3.1.3. Докажите, что если прямая перпендикулярна каждой из двух пересекающихся прямых, лежащих в плоскости, то она перпендикулярна этой плоскости (признак перпендикулярности прямой и плоскости).

Решение. Пусть прямые  и  пересекаются в точке ,  – плоскость, проходящая через эти прямые, прямая  перпендикулярна прямым  и  (рис. 3.7).

На прямых ,  выберем точки , , отличные от точки .  не лежат на одной прямой, поэтому векторы ,

 неколлинеарны. На прямой  выберем точки ,  и обо-

значим . По условию , , следовательно, ,            и          ,

.

Прямая            называется перпендикулярной           плоскости, если она перпендику-

лярна каждой прямой, ле- _{Рис. 3.7} жащей в этой плоскости.

Поэтому рассмотрим произвольную прямую , лежащую в плоскости . Отметим на прямой  точки ,  и вектор . Разложим вектор  по неколлинеарным векторам  и :

.

Умножим обе части этого равенства скалярно на вектор :

Учитывая, что  . Поэтому  и . Следовательно, по определению прямой, перпенди-

кулярной плоскости, . □

Пример 3.1.4. Все плоские углы тетраэдра  при вершине  прямые. Докажите, что квадрат площади грани  равен сумме квадратов площадей остальных граней (одно из пространственных обобщений теоремы Пифагора).

         Решение. Положим   ,

. Тогда , . По

формуле (3.3)

.

Из условия задачи , , . Поэтому

.

,

 соответственно равны

.

Следовательно, . □

Решение следующей задачи демонстрирует отмеченный в предыдущем пункте недостаток векторного метода. В ней очевидный план решения требует при его реализации простых, но достаточно долгих вычислений.

Пример 3.1.5. Вокруг квадрата со стороной  описана окружность. Докажите, что сумма квадратов расстояний от любой точки окружности до прямых, содержащих стороны квадрата, постоянна и равна .

Решение. Пусть  – центр квадрата . Выберем за базисные векторы  и , где ,  – середины сторон  и  соответственно (рис. 3.8). Тогда

, ,

                                               M                                               ,                   .

Радиус окружности, описанной около квадрата со стороной , равен .

Поэтому радиус-вектор

 

                      Рис. 3.8                       произвольной точки  этой окружно-

сти имеет длину , следова-

тельно,

 

и

.

Расстояние  от точки  до прямой  можно найти по формуле (3.5):

.

Очевидно, что

, ,

,

 

,

,

.

Поэтому

 

Аналогично находим

,

, .

Отсюда

                                                                                                                                      

 

 .

Найденная сумма не зависит от выбора точки . Следовательно, сумма квадратов расстояний от любой точки окружности, описанной около квадрата, до прямых, содержащих стороны этого квадрата, постоянна и равна . □

3.1.3. Задачи на вычисление. В значительной части задач, предлагаемых в учебниках и задачниках по геометрии, изучаются свойства треугольника и комбинаций треугольника с другими фигурами. При решении этих задач достаточно часто может быть полезен результат следующей задачи.

Задача 3.2 (теорема Стюарта^[5]). Точка  делит сторону  треугольника  в отношении , считая от вершины . Выразите вектор  через векторы ,  и найдите длину отрезка

, если , , .

Решение. По формуле деления отрезка в данном отношении

.     Введем    обозначения      , ,      тогда

. Найдем скалярный квадрат вектора :

.

По определению скалярного произведения , а из теоремы косинусов , поэтому

.

Следовательно,

. □                          (3.10)

Чтобы использовать теорему Стюарта, как видим, нужно знать отношение , в котором точка  делит отрезок . Сначала обычно приходится вычислять этого отношение. Чаще всего в качестве точки  рассматривается основание медианы, биссектрисы или высоты треугольника. В случае медианы,  – середина отрезка , поэтому . Рассмотрим, как используя векторы, найти  в двух других случаях.

Задача 3.3. Дан треугольник ,  – биссектриса внутреннего (внешнего) угла этого треугольника. Найдите отношение, в котором точка  делит сторону .

Решение. Будем пользоваться обозначениями предыдущей задачи. Пусть отношение, в котором точка делит сторону , считая от точки , равно . Тогда  или, с учетом принятых обозначений,

.

Пусть , тогда точка  делит отрезок  внутренним образом. Найдем единичные векторы  сонаправленные с векторами (из определения произведения вектора на число, например для вектора , имеем: ). Па-

раллелограмм, построенный на единичных векторах , будет ромбом (рис. 3.9), а диагональ ромба является биссектрисой двух его противоположных углов. Поэтому вектор  коллинеарен вектору , и значит,

                                         .

Сравнивая разложения вектора  по неколлинеарным векторам  и , имеем:. Откуда  и, следовательно,

.                             (3.10)

Заметим, что мы получили векторное доказательство хорошо известного факта:  – биссектриса внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам.

Биссектриса  внешнего угла треугольника делит отрезок  внешним образом и перпендикулярна биссектрисе . Поэтому она параллельна вектору м деле,

.

Аналогично доказывается, что в этом случае . Заметим, что на основании теоремы синусов искомое отношение можно также выразить через меры углов треугольника

 □

Задача 3.4. Дан треугольник ,  – его высота. Найдите отношение, в котором точка  делит сторону .

Решение. По условию . Выполнив в этом равенстве замену , получим

. Откуда .

Пусть точка  делит сторону  в отношении , считая от точки , тогда  или . Если умножить обе части последнего равенства скалярно сначала на вектор , а затем

на вектор , то получим одинаков е результаты; поэтому

.

Отсюда следует, что . Учитывая, что  

, найденное отношение можно записать в виде

.

Полученная формула выражает отношение  через длины сторон треугольника . При решении некоторых задач гораздо удобней знать выражение этого отношения через меры углов треугольника. Так как

,

а по теореме синусов , то

. □

В ходе решения планиметрических задач часто приходится вычислять длины медиан, биссектрис и высот треугольника. Покажем, как находить длины этих отрезков, используя рассмотренные опорные задачи.

Пример 3.1.6. Длины сторон , ,  треугольника  равны , ,  соответственно. Найдите длину: а) медианы ; б) биссектрисы  угла ; в) биссектрисы  угла, внешнего к углу ; г) высоты .

Решение. а) Основание  медианы  делит сторону  в отношении . Поэтому из (3.10) находим:

                                  .

б) Точка  делит сторону  в отношении , считая от вершины . Следовательно,

.

Отсюда  или

,

где .

в) Длина биссектрисы  внешнего угла находится аналогично. Выполнив соответствующие преобразования, получим:

.

При , т. е. в том случае, когда треугольник  является равнобедренным с основанием , биссектриса внешнего к  угла параллельна

г) Здесь . Вычисления

C

высоты  с помощью формулы (3.10) сопряжено с громоздкими вычислениями. Поэтому поступим иначе. По-

        скольку, то      A                          H            B

       . Будем считать, что                      Рис. 3.10

 (рис. 3.10), тогда.

Из прямоугольного треугольника  

      .        Преобразуем

подкоренное выражение:

                               

   .

Приходим к известной формуле

. □

Примечание. В треугольнике  длины медиан, проведенных к сторонам , , , принято обозначать , ,  соответственно; высоты, опущенные на стороны , ,  или их продолжения – , , ; а биссектрисы углов , ,  – , , . С учетом этих обозначений:

,

;

,

;

, .

Пример 3.1.7. Медианы , и  треугольника  взаимно перпендикулярны. Найдите сторону , если , .

Решение. Пусть  – точка пересечения медиан (рис. 3.8). Положим ; по условию векторы  взаимно ортогональны, поэтому . Тогда  и

.

_A                                             Медианы треугольника точкой  их пересечения делятся в отношении

, считая от вершины. Поэтому

 и

, .

                                                 C       Отсюда

Рис. 3.8

 

и . Таким образом,

.

Но  и, значит,

. Откуда . □

Пример 3.1.8. Катеты прямоугольного

_B                                             треугольника равны  и , . Через середи-

ну меньшего катета проведена окружность, касающаяся гипотенузы в ее середине. Найдите радиус этой окружности.

Решение. Положим , . Тогда

, , ,

C              E         A                                  ,

         Рис. 3.9                 ,

где  – середина меньшего катета,  – середина гипотенузы. Пусть  – центр окружности и 

.

Окружность касается гипотенузы, поэтому вектор   

ортогонален вектору

                                                                                                           

Отсюда  или

.

По условию , где

.

Преобразуя равенство

,

получим . Откуда . Подставив найденное значение  в равенство, связывающее , имеем:

   Отсюда       и 

. □

Пример 3.1.9. Одна из сторон равностороннего треугольника образует с плоскостью  угол , а другая – угол . Найдите угол между плоскостью треугольника и плоскостью .

Решение. Пусть  – данный треугольник, точка , точки ,  – ортогональные проекции точек ,  на плоскость . Бу-

      дем     считать,     что     ,

 (рис. 3.10). Кроме того,

не нарушая общности рассуждений, условимся считать, что сторона треугольника  равна 1.

Обозначим , , а

        единичный нормальный вектор плос-                    Рис. 3.10

кости  – через . Примем векторы ,

,  за векторы базиса. Согласно принятым соглашениям  

, а из условий задачи следует, что ,

. Имеем следующую таблицу скалярных произведе-

ний базисных векторов:

 

	1
		1
			1

 

Угол между плоскостью треугольника  и плоскостью  можно найти как угол между нормальными векторами этих плоскостей. Нормальный вектор плоскости треугольника, обозначим его через , ортогонален векторам  и , поэтому , .

Разложим вектор  по векторам базиса:

.

Чтобы найти коэффициенты этого разложения, учитывая составленную таблицу, умножим скалярно вектор  на векторы  и :

, .

Рассмотрим найденные соотношения как систему двух линейных уравнений с двумя неизвестными  :

 

Система имеет решение: . Придавая  ненулевые значения и вычисляя соответствующие значения  и , будем получать векторы, перпендикулярные плоскости треугольника

. Положим, например, , тогда

.

Согласно (3.9) искомая величина  двугранного угла между плоскостями равна. Находим:

,

 

Следовательно, . □

Пример 3.1.10. Дан куб  с ребром . Найдите:

а) угол между диагональю куба и скрещивающейся с ней диа-

гональю грани;

б) угол между скрещивающимися диагоналями смежных гра-

ней куба;

в) угол между диагональю  куба и плоскостью ;

г) угол между диагональю  куба и плоскостью ;

д) угол между плоскостями  и ;

е) угол между плоскостями  и ;

ж) расстояние от вершины  до плоскости ;

з) расстояние между скрещивающимися диагоналями смежных

граней куба;

и) расстояние от вершины  до диагонали .

Решение. Присоединим к кубу базис . Векторы этого базиса имеют длину  и попарно ортогональны, т. е. ,

      , .                           C1                                                      B1

а) Найдем, например, угол  

D¹

между диагональю куба  и диагональю  грани . Согласно формуле (3.6):

                           .                                                            B

Разложим векторы  и  по       _{D            A} векторам базиса: _{Рис. 3.}10

      ,                                 

.

Отсюда

                                                    

.

Следовательно, .

б) Найдем угол  между диагональю  грани  и диагональю  грани . Имеем:

,

где  и .

Вычисляя

 

,

находим . Следовательно, (Можно было, разумеется, отложить от вершины  вектор  и заметить, что

 – равнобедренный треугольник.)

в) Поскольку угол между диагональю куба и скрещивающейся

с ней диагональю грани равна (пункт а), то диагональ куба  будет перпендикулярна диагоналям  и  граней, а, значит, и плоскости .

г) Искомый угол  можно найти как угол между вектором  и нормальным вектором плоскости . Так как  и

, то вектор  является нормальным вектором плоскости . По формуле (3.7) . Поскольку  

, то

 

и . Откуда .

д) Так как  – нормальный вектор плоскости  (см. пункт а),  – нормальный вектор плоскости , то в силу предыдущего пункта искомый угол равен .

г) Расстояние  от вершины  до плоскости  равно длине перпендикуляра , опущенного из точки  на эту плоскость. Плоскость  параллельна векторам  

 

Так как вектор ,

 

,

     .

Значит, ,  удовлетворяют системе  решая которую находим:. Поэтому  и .

з) Найдем расстояние между скрещивающимися диагоналями

 и  (пункт б). Согласно (3.6) искомое расстояние равно расстоянию от точки  до плоскости , проходящей через точку  параллельно векторам  и . Пусть  – основание перпендикуляра, опущенного из точки на плоскость . Тогда  

 

 .

Имеем:

 

,  .

Следовательно, ,  удовлетворяют системе  Решая эту систему, находим:. Откуда

 

и) В силу (3.5) расстояние от вершины  до диагонали  грани  можно найти по формуле 

,

где . Имеем: ,

. Отсюда

. □

Пример 3.1.11. Дан правильный тетраэдр  с ребром .

                              D                                  Найдите:

а) угол между его противопо-

ложными ребрами;

б) угол между скрещивающи-

мися медианами смежных граней;

                                                       ^B                   в) угол между плоскостью гра-

A ни и ребром, в ней не лежащим;

г) угол между плоскостями

граней;

C _{Рис. 3.11} д) расстояние между противоположными ребрами;

е) расстояние между скрещивающимися медианами смежных

граней.

Решение. Выберем векторы , ,  в качестве базисных векторов (рис. 3.11). Тогда по условию:

,

.

а) Найдем, например, угол  между ребрами .

Его можно найти как угол между векторами  и  

. Имеем:

.

Следовательно, .

б) Будем искать углы между медианой  грани  и скрещивающимися с ней медианами ,  грани . Угол можно найти как угол между векторами  

. Имеем:

,

,

 

(Разумеется, длины векторов ,  можно было не вычис-

лять, а сразу воспользоваться тем, что длина медианы правильного треугольника со стороной  равна  

Отсюда  и, следовательно, .

Угол между медианами  найдем как угол между векторами . Так как

,

то .

в) Найдем, например, угол между ребром  и плоскостью

. Поскольку плоскость , проходящая через ребро , перпендикулярна плоскости , то искомый угол (обозначим его

) можно найти как угол между векторами  

. Так как  и

,

то  Следовательно, .

г) Плоскость  перпендикулярна ребру , поэтому искомый угол (обозначим его ) найдем как угол между векторами  

. Так как

 

,

то .

д) Расстояние между скрещивающимися ребрами, например

 и , равно длине общего перпендикуляра прямых  и . Этот перпендикуляр лежит на прямой, по которой пересекаются плоскости, проходящие через одну из данных прямых, перпендикулярно другой. В рассматриваемом случае это плоскости  и

, где ,  – середины ребер  и  соответственно. Поэтому длину общего перпендикуляра  более просто найти по теореме Пифагора, например, из прямоугольного треугольника

.

е) В данном случае подход, использованный в предыдущем

пункте, требует дополнительных и неочевидных построений. С помощью векторов, однако, можно формализовать процесс вычислений и совсем не прибегать к построениям.

Вычислим расстояние между медианами  и . Его можно найти как расстояние от точки  до плоскости

, проходящей через прямую  параллельно

прямой . Пусть  – вектор, перпендикулярный плоскости , конец которого лежит в этой плоскости. Тогда , где вектор  компланарен неколлинеарным векторам  

и . Поэтому

 

Так как

 

 

,

 

 

Отсюда

Решая эту систему, находим . Следовательно,

 

и

 

Расстояние между медианами  и  вычисляется аналогично. Его можно найти как расстояние от точки  до плоскости

, проходящей через прямую  параллельно

прямой . Пусть  – вектор, перпендикулярный плоскости , конец которого лежит в этой плоскости. Тогда , где вектор  компланарен неколлинеарным векторам  

. Поэтому

 

Так как

 

 

Отсюда  

Полученная система имеет решение: . Значит,

 

и

 □

Пример 3.1.12. Дан куб  с ребром . Найдите радиус сферы, проходящей через вершину , центр грани  и середины ребер  и .

Решение. Пусть  – середина ребра ,  – середина ребра

,  – центр грани       Примем векторы

, ,  за векторы        базиса.            Тогда            и

                                                               ,            

, .

Если  – радиус-вектор центра  сферы, то

 

или , где

 

, .

Вычисляя

,

,

,

приходим к системе

 

Эта система равносильна системе  Решая ее, на-

ходим: . Откуда

.

Следовательно, радиус сферы равен . □ Пример 3.1.13. Дана правильная четырехугольная пирамида , у которой сторона ос-

нования имеет длину 1, а боковое ребро – длину 2. Сфера касается плоскости основания пирамиды в вершине A и бокового ребра .

Найдите радиус сферы.

Решение. Пусть  – центр сферы, тогда , где  – основа-

ние перпендикуляра, опущенного из точки  на прямую  (рис. 3.13).

Основанием пирамиды является квадрат со стороной 1, поэтому . Из прямоугольного треугольника , где  – центр квадрата , по теореме Пифагора находим .

Выберем векторы , ,  в качестве векторов базиса. По условию задачи 

, .

Вектор

,

поэтому . Откуда . Из тре-

угольника  по теореме косинусов

 или . Отсюда . Аналогично из

треугольника  находим:. Таким образом, таблица скалярных произведений базисных векторов имеет вид:

 

	4		3
		4
	3		4

 

Радиус  сферы перпендикулярен плоскости основания пирамиды, следовательно, вектор  коллинеарен вектору :

.

Пусть . Тогда

                              

Вектор  ортогонален вектору , поэтому , т. е.

.

Заменяя скалярные произведения базисных векторов их значениями, имеем .

Из равенства  следует, что , т. е.

Откуда          

или с учетом значений скалярных произве-

дений базисных векторов .

Таким образом,  и  могут быть найдены из системы

 

Выразим из второго уравнения  через  и подставим в первое уравнение:

,

 

Решая полученное квадратное уравнение , находим . Второй корень является посторонним, т. к. в этом случае сфера касается не ребра , а его продолжения. Поэтому . Отсюда . □

Примечание. Наиболее полно приемы использования векторной алгебры при решении вычислительных задач по стереометрии рассмотрены в учебном пособии С.А. Шестакова [17]. В этом пособии даны образцы решения векторным методом разнообразных задач, традиционно встречавшихся на вступительных экзаменах в вузы и вошедших сегодня в варианты ЕГЭ по математике. В пособии имеется прекрасная подборка задач разной степени трудности для самостоятельного решения. Кстати, автор пособия отмечает и убедительно доказывает, что векторный метод нередко позволяет компенсировать недостаточно развитое пространственное воображение, без которого, как известно, решение трудных стереометрических задач чисто геометрическими методами вызывает значительные затруднения.

 

Задачи для самостоятельного решения

 

79.              Две медианы треугольника равны. Докажите, что треугольник равнобедренный.

80.              Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

81.              Докажите, что сумма квадратов диагоналей параллелепипеда равна сумме квадратов всех его сторон.

82.              Докажите, что сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон и удвоенного произведения оснований.

83.              Докажите, что сумма квадратов расстояний от всех вершин квадрата до прямой, проходящей через его центр, не зависит от выбора прямой.

84.              Докажите, что сумма квадратов расстояний от произвольной точки, взятой в плоскости прямоугольника, до вершин этого прямоугольника в два раза больше суммы квадратов расстояний от этой точки до прямых, содержащих стороны прямоугольника.

85.              Докажите, что сумма квадратов расстояний от фиксированной точки, взятой в плоскости данной окружности, до концов произвольного диаметра этой окружности не зависит от выбора диаметра.

86.              В куб вписана сфера. Докажите, что сумма квадратов расстояний от любой точки сферы до вершин куба не зависит от выбора этой точки.

87.              Точки  и  – середины сторон  и  квадрата ,

 – точка пересечения отрезков  и . Докажите, что отрезок  равен стороне квадрата.

Прямую, пересекающую плоскость, но не перпендикулярную к ней, называют наклонной к этой плоскости.

88 (теорема о трех перпендикулярах). Докажите, что если прямая, лежащая в плоскости, перпендикулярна наклонной, то она перпендикулярна и ортогональной проекции на плоскость этой наклонной, и, обратно, если прямая, лежащая в плоскости, перпендикулярна ортогональной проекции наклонной, то она перпендикулярна и самой наклонной.

89.              В тетраэдре  все плоские углы при вершине  прямые,  – центроид грани . Докажите, что

.

90.              Точка  – центроид треугольника ,  – произвольная точка. Докажите, что:

а) ;

б) .

91.              Докажите, что сумма квадратов ребер тетраэдра равна учетверенной сумме квадратов расстояний от вершин этого тетраэдра до его центроида.

92.              Докажите, что в тетраэдре :

а) ;

б) , где ,  – середины ребер ,  соответственно.

93.              В ромбе  со стороной 6 величина угла  равна . На стороне  взята точка  такая, что . Найдите расстояние от точки  до центра симметрии ромба.

94.              Вычислите расстояние между противоположными сторонами ромба, если длины его диагоналей равны  и .

95.              В остроугольном треугольнике  стороны ,  и высота . Найдите длину перпендикуляра, опущен-

ного из вершины  на медиану, проведенную из вершины .

96.              Отрезки , ,  являются соответственно биссектрисой, медианой и высотой внутреннего угла неравнобедренного треугольника . Найдите отношение , если ,

, .

97.              Найдите угол между медианами катетов равнобедренного прямоугольного треугольника.

98.              В треугольнике  медиана  перпендикулярна стороне . Найдите угол .

99.              В ромбе  точки  и  – середины сторон  и .

Найдите угол , если  

100.          Медиана и высота, проведенные из одной вершины треугольника, разделили угол при этой вершине на три равных угла. Найдите величины углов треугольника.

101.          Окружность, построенная на стороне  треугольника , пересекает стороны ,  в точках  и  соответственно.

Найдите углы треугольника, если , .

102.          Стороны основания прямоугольного параллелепипеда  равны , , высота равна . Найдите угол между

диагоналями параллелепипеда, лежащими в плоскости .

103.          Ребра прямоугольного параллелепипеда равны ,  и . Найдите углы между скрещивающимися диагоналями смежных граней параллелепипеда.

104.          Непересекающиеся диагонали двух смежных боковых граней прямоугольного параллелепипеда образуют с плоскостью основания углы  и . Найдите косинус угла  между этими диагоналями.

105.          Все ребра параллелепипеда равны , а плоские углы, прилежащие к одной вершине равны ,  и . Найдите объем параллелепипеда.

106.          Дан куб  с ребром . Найдите расстояние от середины ребра  до плоскости, проходящей через диагональ  грани  и середину ребра .

107.          В основании прямой призмы , высота которой равна 4, лежит треугольник , в котором ,  и

. Точки , ,  принадлежат ребрам , ,  соответственно, причем , ,  

. Найдите объемы многогранников, на которые плоскость  разбивает данную призму.

108.          Дан тетраэдр . Точки , ,  принадлежат ребрам

, ,  соответственно, причем , ,

. Найдите отношение объемов частей, на которые

плоскость  разбивает данный тетраэдр.

109.          Ребро куба  равно . Найдите радиус

сферы, проходящей через середины ребер ,  и через вершины  и .

110.          Сфера радиуса  с центром на ребре  правильного тетраэдра  касается грани  и пересекает ребро  в точке  такой, что . Найдите ребро тетраэдра.

111.          В правильной треугольной пирамиде длина бокового ребра в три раза больше длины стороны основания. Найдите величину двугранного угла при боковом ребре.

112.          В правильной пирамиде  найдите угол между боковым ребром  и стороной основания .

 

§ 3.2. Двугранные и трехгранные углы

 

3.2.1. Двугранный угол. Двугранным углом называется фигура, образованная двумя полуплоскостями  и  с общей границей  (рис. 3.14). Полуплоскости, образующие двугранный угол, называются его гранями, а общая граница – прямая  – его ребром. Двугранный угол с ребром  и гранями ,  условимся обозначать .

Величина двугранного угла  измеряется величиной его линейного угла, который определяется следующим образом. Пусть  – произвольная точка ребра , лучи ,  (, ) перпен-

дикулярны ребру  (рис. 3.14). Линейным углом двугранного угла называется угол . Очевидно, что величина линейного угла двугранного угла  не зависит от выбора точки , а плоскость любого линейного угла перпендикулярна ребру .

Задача 3.5. Точка  лежит внутри двугранного угла величины  и удаленна от его граней на расстояния  и . Найдите расстояние от точки  до ребра двугранного угла.

Решение. Пусть  – данный двугранный угол,  и  – проекции точки  на грани  и  (рис. 3.15). Тогда ,  и плоскость перпендикулярна ребру . Обозначим точку пересечения плоскости  с ребром  буквой .

Выберем векторы  и  в качестве базисных векторов плоскости . Для этих векторов

.

Разложим вектор , :

.

Найдем коэффициенты  и  этого разложения. Вектор  ортогонален вектору , поэтому, умножая вектор  на

       , получим ; умножая вектор  на

, аналогично находим: . С учетом найденных скалярных произведений умножим по частям векторное равенство

 сначала на вектор , а затем на вектор .

При этом получим:

, .

Следовательно,  и  являются решениями системы

 

Система имеет решение , поэтому

,

 

Искомое расстояние . □

Задача 3.6. Точки  и  принадлежат граням двугранного угла , величина которого равна . Точки  и  – ортогональные проекции этих точек на ребро  (рис. 3.16). Найдите длину отрезка

, если ,  и .

Решение. Выберем векторы , ,  в качестве базис-

ных. Таблица скалярных произведений этих векторов будет иметь следующий вид:

 

	,
			0
			0
	0	0

 

Длина отрезка  равна длине вектора . Век-

тор , поэтому

.

Откуда с учетом таблицы находим:

Таким образом, . □

Биссекторной полуплоскостью двугранного угла называется полуплоскость, границей которой является ребро данного двугранного угла и которая делит его на два равных двугранных угла (рис. 3.17). Любая точка, принадлежащая биссекторной полуплоскости двугранного угла, одинаково удалена от граней этого угла. Следовательно, центры всех сфер, касающихся граней двугранного угла, принадлежат его биссекторной полуплоскости.

3.2.2. Трехгранный угол. Теоремы косинусов и синусов для трехгранного угла. Пусть имеется  плоских углов

, , …, , никакие два из которых не имеют общих

точек, отличных от их общей вершины  или общей стороны, и никакие два угла, имеющие общую сторону, не лежат в одной плоскости. Фигуру, образованную этими углами, называют n-гранным углом и обозначают . В тех случаях, когда  не указывается, для нее употребляется название многогранный угол.

Плоские углы , , …,  называются гранями n-гранного угла , их стороны , , …,  – его ребрами, а точка  – его вершиной.

Две грани многогранного угла, имеющие общее ребро, называются смежными. Двугранный угол между смежными гранями называется двугранным углом многогранного угла.

Многогранные углы бывают выпуклыми и невыпуклыми. Будем рассматривать только выпуклые многогранные углы. Многогранный угол называется выпуклым, если он расположен по одну сторону от плоскости каждой своей грани.

Естественно, что особое место среди многогранных углов занимает трехгранный угол. Если двугранный угол в известном смысле можно считать пространственным аналогом обычного угла, то трехгранный угол – пространственным аналогом треугольника.

Величины плоских и двугранных углов трехгранного угла называют элементами трехгранного угла; величины двугранных углов при ребрах , ,  трехгранного угла  обычно обозначают , , , а величины противоположных им плоских углов

, ,  – , ,  соответственно. Ребра , ,  трехгранного угла часто обозначают , , , а сам угол .

Трехгранный угол с равными плоскими углами называется правильным. Трехгранный угол, все плоские углы которого являются прямыми, называется прямым трехгранным углом.

Пример 3.2.1. Биссектрисы двух плоских углов трехгранного угла перпендикулярны. Докажите, что биссектриса третьего плоского угла перпендикулярна первым двум биссектрисам.

Решение. Пусть биссектрисы плоских углов гранного угла  перпендикулярны. Обозначим через ,  и  

единичные направляющие векторы ребер ,  и  соответственно. Тогда векторы  будут направляю-

щими векторами биссектрис углов         , ,  и 

.

Отсюда и

.

С учетом найденного соотношения

, .

Это означает, что биссектриса угла  перпендикулярна биссектрисам углов  и . □

Пример 3.2.2. Биссектрисы плоских углов ,  и  трехгранного угла  являются ребрами правильного трехгранного угла. Найдите зависимость между плоскими углами трехгранного угла .

Решение. Вновь единичные направляющие векторы ребер ,  и  трехгранного угла обозначим через  соответственно. Тогда 

.

Векторы ,  и  являются направ-

ляющими векторами биссектрис углов , , , при этом

,

,

По условию задачи , поэтому

 

или . Отсюда

,

.

Следовательно, плоские углы трехгранного угла  либо удовлетворяют условию

,

либо – условиям:

.

Поскольку , , , то во втором случае  

, т. е. трехгранный угол  является правильным. □

Для многогранного угла вводится понятие полярного ему многогранного угла. Рассмотрим, как вводится полярный угол, на примере трехгранного угла  (рис. 3.18). Плоскость грани  разбивает пространство на два полупространства. В одном из этих полупространств расположено ребро . Проведем из вершины  луч

, перпендикулярный плоскости  и лежащий в полупространстве, дополнительном к тому, в котором лежит ребро . Аналогично построим лучи , , перпендикулярные плоскостям углов  и  соответственно. Трехгранный угол , ребрами которого

служат лучи , , , называется полярным к данному трехгранному углу .

Отношение полярности трехгранных углов взаимно: если трехгранный угол  полярен трехгранному углу

, то угол  полярен трехгранному углу .

В самом деле, например, ребро  угла  одновременно лежит в гранях  и . Грани  перпендикулярно ребро  угла , а грани  –

      ребро  этого угла. Отсюда следует, что                   ^{Рис. 3.18}

ребро  данного угла перпендикулярно ребрам ,  полярного угла. Поэтому ребро  перпендикулярно плоскости . Таким образом, ребра данного угла перпендикулярны граням полярного.

Из сказанного следует, что плоские углы полярного угла дополняют соответствующие двугранные углы данного угла до . Как условились, величины плоских углов при ребрах , ,  трехгранного угла  обозначим , , , а величины противоположных им плоских углов , ,  – , , .

Тогда

, , .     (3.11)

Так же точно двугранные углы полярного трехгранного угла дополняют соответствующие плоские углы данного:

, , .     (3.12)

Важнейшую роль при изучении свойств треугольников играют теоремы косинусов и синусов, позволяющие находить взаимосвязи между различными элементами треугольника. Оказывается, аналогичные теоремы имеют место и для трехгранных углов. Познакомимся с этими теоремами.

Задача 3.7 (первая теорема косинусов для трехгранного угла). Пусть , ,  – плоские углы трехгранного угла ,  – величина двугранного угла, противолежащего плоскому углу . Докажите, что

.                (3.13)

Решение. На ребрах данного трехгранного угла  отложим единичные векторы ,

                                                                       , ,        где ,

, . Из точек  и  опус-

b a                                              тим перпендикуляры ребро  (рис. 3.19), тогда  и  на

,

 

                                  Рис. 3.19                 и . Поэтому  

.

С другой стороны, учитывая, что , , будем иметь:

 

     .

Таким образом,  или

. □

Задача 3.8 (теорема синусов для трехгранного угла). Пусть , ,  – плоские углы трехгранного угла , , ,  – противолежащие им двугранные углы. Докажите, что

.                              (3.14)

Решение. Возьмем на ребре  некоторую точку  и опустим из нее перпендикуляр  на плоскость угла . В гранях углов  и  проведем из точки  перпендикуляры  и  к ребрам  и  или их продолжениям соответственно (рис. 3.20).

Найдем двумя способами длину перпендикуляра . Из прямоугольных треугольников  и  соответственно имеем: ,  

. Отсюда

.

Из треугольников  и  аналогично получим:

 .

Поэтому

,

и значит,

.

Равенство  доказывается аналогично. □

Пример 3.2.3 (вторая теорема косинусов для трехгранного угла). Пусть , ,  – двугранные углы трехгранного угла ,  – величина плоского угла, противолежащего двугранному углу . Докажите, что

.               (3.15)

Решение. Применим первую теорему косинусов к трехгранному углу , полярному данному углу : 

.

Отсюда, учитывая, что из соотношений (3.11), (3.12)

, , , ,

получим

 

.

С помощью формул приведения приходим к равенству (3.15), которое требуется доказать. □

Пример 3.2.4. Пусть , ,  – плоские углы трехгранного угла

; , ,  – углы, образованные ребрами , ,  с плоскостями противоположных им граней. Докажите, что

.

Решение. На рисунке 3.20:  – точка ребра ,  – перпендикуляр, опущенный из этой точки на плоскость угла . Поэтому  и . Но тогда из решения задачи 3.8 следует, что . Отсюда находим:

.

Если аналогично выбрать точки на ребрах ,  и опустить из них перпендикуляры на плоскости граней, противоположных этим ребрам, можно получить соотношения:

, .

Из найденных равенств заключаем: 

. □

С помощью доказанных теорем открывается возможность изучать свойства плоских и двугранных углов трехгранного угла, успешно решать вычислительные задачи на вычисление плоских и двугранных углов многогранников.

Пример 3.2.5. Величина любого плоского угла трехгранного угла меньше суммы величин двух других его плоских углов, но больше их разности.

Решение. Проведем доказательство для плоского угла . Так

как , , , то при  двойное неравенство

 

очевидно. Докажем его для случая . Будем при этом считать, что . Из соотношения (3.13) имеем:

.

Двугранный угол , поэтому  и, значит,

.

Учитывая, что , отсюда последовательно заключаем:

;

; .

На промежутке  функция  монотонно убывает. Поэтому при  двойное неравенство  также справедливо. □

Пример 3.2.6. В тетраэдре  ребра , ,  равны ,

,  соответственно, а противолежащие им плоские углы при вершине  – , ,  соответственно. Найдите объем тетраэдра.

Решение. Пусть  – высота тетраэдра,  – высота грани

. Тогда по теореме о трех перпендикулярах  и  – линейный угол двугранного угла с ребром .

Найдем высоту  тетраэдра. _A По условию . Из прямоугольного треугольника  на-

ходим: .          Величину        B угла  обозначим через . Из первой теоремы косинусов для D трехгранного угла имеем:

                   .                                            C

       Отсюда                                                                   Рис. 3.21

.

Из треугольника  находим: . Итак,

                                 

Площадь грани . Следовательно,

 

. □

Пример 3.2.7. В правильной четырехугольной пирамиде  плоский угол при вершине  равен . Найдите: а) двугран-

ный угол при ребре основания, б) двугранный угол при боковом ребре, в) угол между боковым ребром и плоскостью основания.

Решение. Основанием правильной четырехугольной пирамиды  является квадрат , ее боковые грани – равнобедрен-

ные треугольники с углом  в общей вершине и с углами  при

_S                      основании. Двугранный угол при ребре основания, двугранный угол при боковом ребре и угол между боковым ребром и плоскостью основания пирамиды обозначим чеD    рез ,  и  соответственно.

а, б) В трехгранном угле  два плоских угла равны

     B                                      A                   , третий плоский угол прямой.

Рис. 3.22

Двугранные углы  и  при ребре

основания и при боковом ребре можно найти по первой теореме косинусов для трехгранного угла.

В этом трехгранном угле ребро основания, например , лежит против плоского угла (рис. 3.22), поэтому

 

и .

Боковое ребро  лежит против прямого угла , поэтому

 

и .

в) Угол  можно найти из трехгранного угла  по второй

теореме косинусов. В этом трехгранном угле двугранные углы при ребрах , ,  равны  соответственно; угол  

лежит против ребра . Поэтому

 

 

и . □

Пример 3.2.8. В трехгранном угле  плоские углы

, , двугранный угол с ребром  прямой.

Найдите величину двугранного угла с ребром .

Решение. По теореме синусов для трехгранного угла  

. Откуда . Из условий задачи следует,

что . Следовательно,

. □

Пример 3.2.9. Докажите, что в трехгранном угле: а) сумма двугранных углов больше , б) сумма плоских углов меньше .

Решение. а) По второй теореме косинусов для трехгранного угла . Преобразуем правую часть этого равенства:

 .

Отсюда

.

       Так как , ,                      , то

.

Поэтому  и .

б) Двугранные углы , ,  трехгранного угла , полярного данному трехгранному углу , и плоские углы данного связаны соотношениями (3.12):

, , .

Отсюда . По доказанному  

, поэтому . □

3.2.3. Трехгранный угол и сфера. Биссекторные полуплоскости двугранных углов трехгранного угла имеют общий луч с началом в вершине трехгранного угла, который лежит внутри этого трехгранного угла. Этот луч называется биссектрисой трехгранного угла.

Сфера называется вписанной в трехгранный угол, если она касается всех его граней (рис. 3.23). Центры всех сфер, вписанных в трехгранный угол, лежат на биссектрисе этого угла.

                C                                                C

                                       Рис. 3.23                                                Рис. 3.24

Наряду со сферами, вписанными в трехгранный угол, часто рассматриваются сферы, касающиеся всех его ребер (3.24). Некоторые авторы называют такие сферы полувписанными в трехгранный угол. Центры всех сфер, полувписанных в трехгранный угол, принадлежат лучу с началом в вершине трехгранного угла, по которому пересекаются полуплоскости, перпендикулярные граням трехгранного угла и проходящие через биссектрисы плоских углов, лежащих в этих гранях.

Рассмотрим схему рассуждений, позволяющих найти сферу, вписанную в трехгранный угол, зная его элементы.

Пусть сфера  радиуса  с центром в точке  касается граней

, ,  трехгранного угла  в точках , ,  соот-

ветственно (рис. 3.23). Расстояние от центра сферы  до вершины  трехгранного угла обозначим через .

Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен этой плоскости. Поэтому векторы ,

,  будут нормальными векторами плоскостей ,

,  соответственно. При этом ,

, где, как обычно, , ,  – двугранные углы трехгранного угла при ребрах , ,  соответственно.

Выберем векторы , ,  в качестве базисных. Таблица скалярных произведений этих векторов будет иметь вид:

 

Разложим вектор  по базисным векторам:

.

Найдем коэффициенты этого разложения. Воспользуемся для этого тем, что векторы

,

,  

ортогональны векторам , ,  соответственно:

                     , ,      .

Отсюда следует, что

 

или с учетом таблицы скалярных произведений базисных векторов

                        (3.16)

Таким образом, чтобы найти коэффициенты разложения вектора  по базисным векторам необходимо решить систему (3.16) трех линейных уравнений с тремя неизвестными, , . Те, кто знаком с правилом Крамера или методом Гаусса (методом последовательного исключения неизвестных), могут сделать это достаточно легко и быстро. Остальным предлагается проверить, что система (3.16) имеет решение:

,

 

,              (3.17)

 

.

Заметим, что вектор  лежит на биссектрисе трехгранного угла , т. е. на луче, по которому пересекаются биссекторные полуплоскости его двугранных углов.

Расстояние от центра сферы  до вершины  трехгранного угла равно . Следовательно, расстояние  и радиус сферы  связаны соотношением:

.

Найдя решение системы (3.16) и зная одну из этих величин, можно вычислить другую величину. Решение этой задачи в общем виде сопряжено с громоздкими вычислениями, поэтому проводить их не будем. Заметим лишь следующее.

Для решения задач с конкретными числовыми данными нет необходимости запоминать вид системы (3.16) и, тем более, формулы (3.17). В подобных случаях на основе данных, содержащихся в условии задачи, обычно просто воспроизводят с ними проведенные общие рассуждения.

Пример 3.2.10. Сфера радиуса 1 вписана в трехгранный угол, два плоских угла которого равны , а третий угол – . Найдите расстояние от центра сферы до вершины трехгранного угла.

Решение. Воспользовавшись первой теоремой косинусов для трехгранного угла, найдем двугранные углы данного трехгранного угла. Обозначим его  и будем считать, что ,

. Тогда

,

Теперь задача сведена к задаче, рассмотренной в общем виде.

Пусть  – центр сферы и она касается граней , ,  трехгранного угла  в точках , ,  соответственно. Искомое расстояние от центра сферы  трехгранного угла обозначим через . Векторы выберем в качестве базисных. Тогда , ,

, и таблица скалярных произведений базис-

ных векторов будет выглядеть следующим образом:

                

 

Разложим вектор       по базисным векторам:

.

Повторяя рассуждения, проведенные в общем случае, придем к системе

 

Выразим из третьего уравнения системы неизвестное  через неизвестные ,  и подставим в первые два уравнения:

 

Отсюда следует, что система имеет единственное решение  

. Следовательно,

.

Откуда 

 

 

и . □

При вычислении расстояния  от центра  сферы радиуса , касающейся ребер трехгранного угла , потребуется дополнительно знать расстояние от вершины угла  до точек касания. Здесь общая схема рассуждений выглядит следующим образом.

Пусть сфера  радиуса  с центром в точке  касается ребер

, ,  трехгранного угла  в точках , ,  соответст-

венно (рис. 3.24). Будем считать заданными величины плоских углов , ,  трехгранного угла ; их, как обычно, обо-

значать , ,  соответственно. Расстояние от центра сферы  до вершины  трехгранного угла обозначим буквой . Отрезки ,

,  касательных, проведенных из точки  к сфере , будут равны; обозначим их длину буквой .

Поскольку известны величины плоских углов трехгранного угла, то теперь в качестве базисных векторов удобно выбрать векторы . Тогда  ,

, , и таблица скалярных произведений базисных векторов имеет вид:

 

 

Найдем коэффициенты разложения вектора

 

по векторам базиса. Радиусы , ,  сферы перпендикулярны касательным , ,  к этой сфере. Поэтому векторы

,

,  

ортогональны векторам

, , .

Отсюда следует, что

, ,  

или с учетом таблицы скалярных произведений базисных векторов

                        (3.18)

Таким образом, коэффициенты , ,  разложения вектора  по базисным векторам являются решением системы (3.18). Проверьте, что решение этой системы можно записать в виде:

,

 

,              (3.19)

 

.

Множество всех точек пространства, равноудаленных от двух данных пересекающихся прямых, есть две плоскости, перпендикулярные плоскости, в которой лежат эти прямые, и проходящие через биссектрисы углов данных прямых. Рассмотрим плоскости, проходящие через биссектрисы плоских углов трехгранного угла  перпендикулярно плоскостям этих углов. Плоскость , про-

ходящая через биссектрису угла  перпендикулярно плоскости этого угла, является множеством точек одинаково удаленных от ребер  и  или их продолжений. Так же точно, плоскость , проходящая через биссектрису угла  перпендикулярно плоскости этого угла, является множеством точек одинаково удаленных от ребер  и  или их продолжений. Поэтому все точки прямой, по которой пересекаются плоскости  и , будут одинаково удалены от ребер  и  или их продолжений, и, следовательно, принадлежат плоскости , проходящей через биссектрису угла  перпендикулярно плоскости этого угла. Линию пересечения

плоскостей ,  и  часто называют биссекторной прямой трехгранного угла (не путать с биссектрисой трехгранного угла). Из сказанного следует, что точка  принадлежит биссекторной прямой трехгранного угла , а вектор  является направляющим вектором этой прямой.

Расстояние от центра сферы  до вершины  трехгранного угла равно . Следовательно,  и длина  отрезка касательной к сфере , проведенной из точки , связаны соотношением:

.

Радиус  сферы и отрезок касательной к сфере, проведенной из вершины , являются катетами прямоугольного треугольника с гипотенузой . Следовательно, по теореме Пифагора

.

Поэтому, зная две из величин ,  и , можно находить третью.

Пример 3.2.11. Сфера касается ребер трехгранного угла, плоские углы которого равны . Расстояние от центра сферы до вершины трехгранного угла равно . Найдите радиус сферы.

Решение. Обозначим трехгранный угол  и будем считать, что . Пусть  – центр сферы, и она касается ребер , ,  трехгранного угла в точках , ,  соответственно. Выберем векторы , ,  в качестве базисных векторов. Обозначив , составим таблицу их скалярных произведений:

 

 

Найдем коэффициенты разложения вектора

.

по базисным векторам. Теперь, повторяя рассуждения, проведенные в общем случае, получим систему:

 

Выражая из третьего уравнения системы  через ,  и подставляя в первые два уравнения, получим систему:

  

Из первых двух уравнений системы находим: , .

Подставив найденные значения ,  в третье уравнение, имеем:

. Итак,

.

Отсюда

 

По условию задачи , откуда  и

. □

Пример 3.2.12. Расстояние от центра сферы, вписанной в правильную треугольную пирамиду, до вершины пирамиды в два раза больше радиуса сферы. Найдите: а) величину двугранного угла при боковом ребре пирамиды, б) величину плоских углов при вершине пирамиды в) величину двугранного угла между плоскостью боковой грани и плоскостью основания.

Решение. а) Пусть  – данная правильная пирамида,  – центр вписанной в пирамиду сферы,  – радиус сферы,  – величина равных плоских углов при вершине пирамиды,  – величина равных двугранных углов при боковом ребре пирамиды.

Точки касания сферы с боковыми гранями , ,  пи соответственно. Выберем векторы

, ,  в качестве векторов базиса. Тогда

, , и таблица скалярных

произведений базисных векторов будет выглядеть следующим образом:

 

 

Пусть . Система (3.18) в данном случае принимает вид:

 

Сравнивая правые части уравнений системы, заключаем, что

.

Таким образом,  и

.

По условию , поэтому

.

Преобразуем полученное тригонометрическое уравнение:

, .

Отсюда , поэтому .

б) Из второй теоремы косинусов для трехгранного угла нахо-

дим

 

следовательно, .

в) Пусть  – величина двугранного угла при ребре основания пирамиды. В основании правильной треугольной пирамиды лежит равносторонний треугольник, поэтому один из углов при вершине основания пирамиды равен . Боковые грани пирамиды – равнобедренные треугольники с углом  при вершине. Поэтому два других угла при вершине основания равны . Значит, из первой теоремы косинусов для трехгранного угла имеем:

. 

Так      как ,      то

. □

 

Задачи для самостоятельного решения

 

113.          Дан двугранный угол величины . На одной грани этого угла лежит точка , удаленная на расстояние  от другой грани.

Найдите расстояние от точки  до ребра двугранного угла.

114.          Точки  и  принадлежат ребру, а точки  и  граням двугранного угла, при этом . Найдите величину двугранного угла.

115.          Точки  и  принадлежат ребру, а точки  и  граням двугранного угла, величина которого равна  (). Известно, что , . Найдите косинус угла .

116.          Докажите, что любая точка, принадлежащая биссекторной полуплоскости двугранного угла, одинаково удалена от граней этого угла.

117.          Точка  принадлежит ребру двугранного угла, точка  – его биссекторной полуплоскости. Докажите, что прямая  образует равные углы с гранями двугранного угла.

118.          Сфера радиуса  касается граней прямого двугранного угла. Найдите: а) расстояние от центра сферы до ребра двугранного угла, б) расстояние между точками касания.

119 (теорема синусов для двугранного угла). В одной из граней двугранного угла, величина которого равна , проведена прямая, образующая угол  с ребром двугранного угла. Найдите угол наклона этой прямой к другой грани.

120.            Дан двугранный угол величины . Сфера радиуса  касается граней данного двугранного угла. Найдите: а) расстояние от центра сферы до ребра двугранного угла, б) расстояние между точками касания.

121.            Из вершины  прямого трехгранного угла  проведен луч , образующий с ребрами углы ,  и . Докажите, что

.

122.            Докажите, что если двугранные углы трехгранного угла прямые, то его плоские углы тоже прямые.

123.            Найдите угол между биссектрисами плоских углов прямого трехгранного угла.

124.            Докажите, что в произвольном трехгранном угле биссектрисы двух плоских углов и угла, смежного с третьим плоским углом, лежат в одной плоскости.

125.            Плоскость пересекает ребра прямого трехгранного угла в точках ,  и . Докажите, что треугольник  остроугольный.

126.            Точка  принадлежит внутренней области прямого трехгранного угла и удалена от его граней на расстояния ,  и . Найдите расстояние от точки  до вершины трехгранного угла.

127.            Докажите, что если по крайней мере два плоских угла трехгранного угла не прямые, то три плоскости, каждая из которых проходит через ребро трехгранного угла перпендикулярно к плоскости противоположной грани, пересекаются по одной прямой.

128.            Докажите, что плоскости, каждая из которых проходит через ребро трехгранного угла и биссектрису противоположного плоского угла, пересекаются по одной прямой.

129.            В трехгранном угле  плоские углы  и  рав-

ны. Докажите, что биссекторная полуплоскость двугранного угла с ребром  перпендикулярна грани .

130.            Докажите, что в трехгранном угле против равных двугранных углов лежат равные плоские углы и, обратно, против равных плоских углов лежат равные двугранные углы.

131.            Докажите, что в трехгранном угле против большего двугранного угла лежит больший плоский угол и, обратно, против большего плоского угла лежит больший двугранный угол.

132.            Докажите, что если все плоские углы трехгранного угла тупые, то и все его двугранные углы тоже тупые.

133.            Докажите, что если все двугранные углы трехгранного угла острые, то и все его плоские углы тоже острые.

134.            Сумма плоских углов трехгранного угла равна . Докажите, все плоские углы острые.

135.            Докажите, что сумма двугранных углов тетраэдра больше

.

136.            В трехгранном угле  плоские углы , ,  равны , ,  соответственно. Найдите величину двугранного угла с ребром .

137.            В трехгранном угле один из плоских углов прямой, а меры прилежащих к нему двугранных углов равны . Найдите меру третьего двугранного угла.

138.            В трехгранном угле  меры плоских углов ,  и двугранного угла с ребром  равны . Найдите величину двугранного угла с ребром .

139.            В треугольной пирамиде  боковые ребра , ,  равны,  – прямой, . Найдите меру двугранного угла при ребре основания .

140.            В трехгранном угле два плоских угла острые и равны , третий плоский угол равен . Найдите угол  между гранью угла  и противолежащим ей ребром.

141.            Дан трехгранный угол  такой, что ,

, . Найдите косинус угла  между ребром  и биссектрисой угла .

142.            Плоский угол при вершине правильной четырехугольной пирамиды равен . Найдите угол между плоскостями противоположных боковых граней.

143.            Дана треугольная пирамида  такая, что ,  

, , , , . Найдите площадь  основания .

144.            Дана правильная n-угольная пирамида. Найдите:

a) двугранные углы при основании пирамиды, если плоские

углы при основании боковых граней равны ;

б) углы боковых граней, если двугранные углы при основании

пирамиды равны ;

в) двугранные углы при основании пирамиды, если боковые

ребра образуют с плоскостью основания углы ;

г) двугранные углы при боковых ребрах пирамиды, если дву-

гранные углы при основании равны ;

д) двугранные углы при основании пирамиды, если двугран-

ные углы при боковых ребрах равны ;

е) двугранные углы при боковых ребрах, если плоские углы

при вершине пирамиды равны .

145.                    Плоские углы трехгранного угла равны , , , противолежащие им двугранные углы равны , ,  соответственно. Докажите, что

.

146.                    Дан трехгранный угол  такой, что ,

, . Луч  образует с ребрами трехгранного угла углы, равные . Найдите .

147.                    Сфера касается всех ребер правильного трехгранного угла с плоским углом . Найдите радиус сферы, если радиусы окружностей, по которым грани трехгранного угла пересекают сферу, равны 1.

148.                    Дана сфера радиуса 2. Через ее центр проведены три попарно перпендикулярные плоскости. Найдите радиус сферы, которая касается всех этих плоскостей и данной сферы.

149.                    Сфера радиуса 1 касается всех ребер трехгранного угла с плоскими углами , , . Найдите расстояние от вершины угла до центра сферы.

150.                    В двугранный угол, величина которого равна , вписаны две касающиеся друг друга сферы радиуса . Найдите радиус третьей сферы, вписанной в данный угол и касающейся обеих данных сфер.

151.                    Ребро куба  равно 1. Найдите радиус сферы, проходящей через вершину  и касающейся ребер ,  и .

152.                    Сфера, проходящая через вершины ,  и середины ребер

,  правильного тетраэдра , имеет радиус . Найдите ребро тетраэдра.

153.                    Через каждое ребро двугранного угла проведена плоскость, перпендикулярная плоскости его противоположной грани.

Докажите, что эти три плоскости имеют общую прямую.

Указанные плоскости часто называют высотными плоскостями трехгранного угла, а прямую их пересечения – его ортоосью.

 

§ 3.3. Замечательные точки треугольника и тетраэдра

 

В § 2.3 были изучены векторные соотношения для центроидов треугольника и тетраэдра и даны примеры их применения при решении задач. В этом параграфе рассматриваются некоторые соотношения для центров окружностей, описанных около треугольника и вписанных в него; вводится понятие ортоцентрического тетраэдра; изучаются зависимости между замечательными точками треугольника и замечательными точками ортоцентрического тетраэдра.

3.3.1. От треугольника к тетраэдру. Пусть  – данный треугольник. Будем, как обычно, считать, что длины его сторон , ,  равны , ,  соответственно, а противолежащие им углы равны ,  и  соответственно.

Задача 3.9. Докажите, что при любом выборе точки :

–                    радиус-вектор  центра  окружности, описанной около треугольника , имеет вид

;                   (3.23)

–                    радиус-вектор  точки  пересечения двух биссектрис треугольника  имеет вид

;                                (3.24)

–                    радиус-вектор  точки  пересечения двух высот непрямоугольного треугольника  имеет вид

.                         (3.25)

Решение. Воспользуемся для доказательства соотношений (3.23) – (3.25) опорной задачей 2.3 предыдущей главы. Согласно результату этой задачи, если на прямых  и , содержащих стороны треугольника , взяты соответственно точки  и , которые делят стороны треугольника в отношениях ,

, то при любом выборе точки  радиус-вектор  точ-

       ки пересечения прямых           имеет вид:

.

а) Если  – центр окружности, описанной около треугольника

, а  – ее радиус, то . Центр  является

точкой пересечения серединных перпендикуляров к сторонам треугольника. Когда треугольник остроугольный, центр  лежит внутри треугольника, когда – прямоугольный, – на середине гипотенузы, и когда – тупоугольный, – вне треугольника.

Пусть диаметр описанной около треугольника  окружности, проведенный через вершину , пересекает сторону  в точке , а диаметр, проведенный через вершину , пересекает сторону  в точке .

                  Рассмотрим случай остроугол^ь-                       _A B

ного треугольника (рис. 3.25). Очевидно, что , где

, , ,  – площади

треугольников , , ,  соответственно. Отсюда

на основании свойств пропорций . Поскольку центральный угол  опирается на ту же дугу окружности, что и вписанный угол , то , и значит,  

. На том же основании . Поэтому

, т. е. . Аналогичным образом заключаем, что . Самостоятельно убедитесь, что найденные отношения имеют место для прямоугольного и тупоугольного треугольников.

Подставляя в опорную формулу  вместо  и найденные от-

ношения, получим  или

.

б) Пусть биссектрисы  и  

^C                                                треугольника  пересекаются в точке  (рис. 3.26). В силу задачи 3.3 основание  биссектрисы  делит

B                                                        сторону  в отношении , а основание  биссектрисы  – сторону  в отношении .

A                                                 B

                    Рис. 3.26                         Поэтому _или

в) Пусть  – непрямоугольный треугольник, – точка пе-

ресечения его высот  и . Если треугольник остроугольный, то точка  находится внутри треугольника, а если – тупоугольный, то – вне треугольника (рис. 3.27).  В первом случае

, ; , .

Отсюда .

Во втором случае

, ;

, .

Рис. 3.27

Поскольку точки ,  делят теперь стороны треугольника внешним образом, то также получим:

.

Подставляя в общую формулу  вместо  и найденные отношения,

находим:  или 

. □

Если в формулах (3.23) – (3.25) в качестве точки  взять вершину  треугольника  и положить , то получим разложения векторов , ,  по векторам  и :

,       (3.26)

 

,                         (3.27)

 

.                (3.28)

Следует заметить, что при решении задач эти разложения используются гораздо чаще, чем формулы (3.23), (3.24), (3.25).

Заменяя в формулах (3.23), (3.24), (3.25) точку  точками , ,  соответственно получим векторные равенства:

,

,

.

При рассмотрении применений теоремы Чевы были доказаны теоремы о пересечении биссектрис и высот треугольника. Эти теоремы можно доказать, опираясь на результаты задачи 3.9.

Пример 3.3.1. Докажите, что биссектрисы треугольника пересекаются в одной точке.

Решение. Пусть биссектрисы ,  углов  и  треугольника  пересекаются в точке  (рис. 3.26). Докажем, что биссектриса  угла  также проходит через точку .

Установим коллинеарность вектора  вектору . В силу формулы (3.. Как было отмечено, разложение вектора  по векторам ,  можно получить, если в формуле

(3.23) в качестве точки  взять вершину , тогда .

Поэтому  или

.                                  (3.29)

Таким образом, векторы  и  коллинеарны, а значит, биссектриса  угла  также проходит через точку . □

Точка  является центром окружности, вписанной в треугольник .

Теорема о пересечении высот треугольника доказывается аналогично. Проведите это доказательство самостоятельно. Мы же рассмотрим еще один способ ее доказательства.

Пример 3.3.2. Докажите, что прямые, содержащие высоты треугольника, пересекаются в одной точке.

Решение. Пусть прямые, содержащие высоты ,  треугольника  пересекаются в точке  (рис. 3.27). Докажем, что прямая, содержащая третью высоту  треугольника, также проходит через точку

Так как , , то , . Вос-

пользуемся первым из тождеств опорной задачи 3.1. Возьмем в этом тождестве в качестве точки

.

Второе и третье слагаемые в записанной сумме равны нулю, следовательно, . Отсюда следует, что , и значит, прямая, содержащая высоту треугольника , опущенную из вершины , также проходит через точку . □

Напомним, что точка  называется ортоцентром треугольника.

Пример 3.3.3. Диаметры описанной около треугольника  окружности, проведенные через вершины , ,  треугольника, пересекают его стороны , ,  в точках , ,  соответственно. Найдите отношения, в которых центр  описанной окружности делит отрезки ,  и .

Решение. В ходе решения задачи 3.9 было установлено, что

. Поэтому

.

Подставляя в формулу (3.23)  вместо , получаем:

.

Следовательно,

,

 

Откуда и

.

По аналогии находим

.

Пример 3.3.4. Найдите отношения, в которых биссектрисы треугольника  делятся точкой  их пересечения.

Решение. Перепишем соотношение (3.29) в виде

.

Отсюда , т. е. . Следова-

       тельно,     .      Аналогично     находятся      отношения

. □

Пример 3.3.5. Найдите отношения, в которых высоты непрямоугольного треугольника  делятся точкой  их пересечения.

Решение. Снова реализуем идею, использованную в двух предыдущих задачах. Учитывая, что (задача 3.4), имеем:

.

Выбирая в (3.25) в качестве полюса точку , получим:

.

Отсюда  и

.

Переписывая найденное соотношение в виде ,

находим: , т. е. . Отношения

 вычисляются аналогично. □

Сходство свойств медиан и центроидов треугольника и тетраэдра, а также методов их доказательства приводит к мысли, что аналогичная ситуация возникнет и при изучении свойств остальных замечательных точек и линий тетраэдра. Эта мысль подкрепляется тем, что биссектрисы трехгранных углов тетраэдра пересекаются в одной точке – центре вписанной в тетраэдр сферы, а плоскости, перпендикулярные ребрам тетраэдра и проходящие через их середины, пересекаются в одной точке – центре сферы, описанной около тетраэдра.

Поэтому поставим задачу, найти аналоги разложений (3.27) – (3.29) для тетраэдра.

Рассмотрим тетраэдр . Будем считать, что он задан тремя ребрами, инцидентными одной вершине, и углами между ними. Пусть, например, ,

. Выберем векторы , ,  в качестве

базисных. В соответствии с принятыми договоренностями таблица их скалярных произведений будет иметь следующий вид:

 

 

Начнем со сферы, описанной около тетраэдра. Множество всех точек пространства, равноудаленных от двух данных точек, есть плоскость, проходящая через середину отрезка с концами в данных точках перпендикулярно этому отрезку. Легко доказывается, что все плоскости, перпендикулярные ребрам тетраэдра и проходящие через их середины, пересекаются в одной точке. Эта точка и является центром сферы, описанной около тетраэдра.

Пусть  – центр,  – радиус сфе-

ры, описанной около тетраэдра  D (рис. 3.28). Тогда  

. Центр сферы  опреде-

ляется пересечением плоскостей, _C проходящие через середины ребер

, ,  перпендикулярно этим           B ребрам.

Найдем для примера разложе-

ние вектора с началом в вершине  _A тетраэдра и с концом в центре  Рис. 3.28 сферы по базисным векторам:

 

Из равенств

 

имеем:

, ,  

или 

, .

   Так как      

, то последние скалярные произведения мож-

но переписать следующим образом:

, , .

Отсюда

.

Вычисляя скалярные произведения в левых частях этих равенств, приходим к системе трех линейных уравнений с тремя неизвестными ,  и :

 

Система имеет решение, где

,

,

,

После весьма громоздких вычислений найдем:

,

где

 

,         .

Понятно, что запоминать найденные формулы не имеет никакого смысла. Однако сама схема рассуждений при решении задач с конкретными числовыми данными может быть весьма эффективной.

Кроме того, простую для запоминания и полезную формулу можно получить, если найти геометрический смысл выражений  и . Из результата примера 3.2.6 сразу заключаем, что

,

где  – объем тетраэдра.

Положим теперь , , . Тогда по теореме косинусов для треугольника

.

Поэтому

 

Раскрыв скобки и приведя подобные члены, найдем:

.

Отсюда

 

,

где . Следовательно,

,

где, согласно формуле Герона,  – площадь треугольника со сторонами

, , .

Таким образом,

.                                            (3.30)

Пример 3.3.6. Около правильного тетраэдра описана сфера радиуса . Найдите ребро тетраэдра.

Решение. Пусть  – данный тетраэдр, его грани – правильные треугольники. Обозначим длину ребра тетраэдра буквой  и векторы , ,  выберем в качестве базисных.

Таблица их скалярных произведений будет иметь вид:

 

 

Поэтому коэффициенты разложения вектора

,

где  – радиус описанной около тетраэдра сферы, будут решением системы

 

Система имеет единственное решение  и, следовательно,

,

.

Отсюда . □

Теперь рассмотрим сферу, вписанную в тетраэдр. Пусть  – центр сферы, вписанной в тетраэдр ,  – ее радиус. Вновь нетрудно доказать, что центр  сферы является точкой пересечения биссекторных полуплоскостей (биссектрис) трехгранных углов тетраэдра. Отрезок биссектрисы трехгранного угла тетраэдра, соединяющий вершину тетраэдра с точкой противоположной грани, называют биссектрисой тетраэдра.

Для того чтобы найти разложение вектора  по векторам

, , , решим следующую задачу.

Пример 3.3.7. Докажите, что биссекторная полуплоскость двугранного угла при ребре тетраэдра делит противоположное ребро на части, пропорциональные площадям граней тетраэдра, заключающих этот угол.

Решение. Пусть дан тетраэдр . Рассмотрим биссекторную полуплоскость ,  двугранного угла, например,

при ребре  (рис. 3.29). Пирамиды  и  имеют общую вершину , а их основания лежат в одной плоскости. Следовательно, они имеют общую высоту, а их объемы относятся как площади оснований: . При этом треугольники  

и  имеют общую вершину , а их основания лежат на одной прямой, поэтому . Итак,

.

C

С другой стороны, точка  принадлежит биссекторной полуплоскости двугранного угла при ребре , а значит, она равноудалена от плоскостей  и . Отсюда следует, что высоты тетраэдров, опущенные из вершины , равны, и .

Таким образом, . □

Если сравнить доказанное утверждение с теоремой о биссектрисе угла треугольника, то видим, что между ними существует определенная аналогия.

Вернемся к поставленной задаче. Для краткости введем сле-

дующие обозначения площадей граней тетраэдра: ,

, , .

Из утверждения, доказанного в примере 3.3.7, заключаем:

,

где , ,  – точки пересечения биссекторных полуплоскостей при ребрах , ,  с противоположными ребрами тетраэдра.

Из первого отношения следует, что 

.

Второе и третье отношения позволяют выразить вектор биссектрисы тетраэдра, проведенной из вершины :

 

(задача 3.2).

Аналогично находим. Откуда

.

Вектор , где  – центр  сферы, вписанной в тетраэдр , с одной стороны, коллинеарен вектору :

.

С другой стороны, точка  делит отрезок  в некотором отношении λ, считая от точки , т. е.

.

Поэтому  или

.

Отсюда

 

и . Таким образом,

.                                 (3.31)

Для тетраэдра получен аналог формулы (3.27). Можно пойти дальше. Пусть  – произвольная точка пространства. Тогда из найден-

ной формулы имеем: . Следовательно,

.                         (3.32)

Следует заметить, что полученные формулы при решении задач, в которых рассматриваются сферы, вписанные в тетраэдр, используются крайне редко. В этих задачах, как правило, применяется формула

,

где  – радиус вписанной в тетраэдр сферы,  – его объем. Полезно также знать формулы для вычисления объема, приведенные в задаче 159.

Еще большее разочарование мо-

D жет возникнуть при изучении взаимного расположения прямых, содержащих высоты тетраэдра. Если в любом треугольнике прямые, содержа-

B щие его высоты, пересекаются в одной точке, то среди тетраэдров суще-

A ствуют такие, у которых высоты

(точнее, содержащие их прямые) в C одной точке не пересекаются.

                         ^{Рис. 3.30}                              Рассмотрим, например, тетраэдр

, у которого угол  грани  не является прямым, а ребро  перпендикулярно плоскости этой грани (рис. 3.30). Высота это-

го тетраэдра, проведенная из вершины , лежит на прямой , а высота, опущенная из вершины , лежит в плоскости  (по признаку перпендикулярности двух плоскостей, плоскости  и  перпендикулярны). Так как угол  не является прямым, основание  высоты, опущенной из вершины , не совпадает с точкой .

Следовательно, ,  – скрещивающиеся прямые.

Тетраэдры, у которых прямые, содержащие высоты, пересекаются в одной точке, называют ортоцентрическими. Точка пересечения высот ортоцентрического тетраэдра называется его ортоцентром. Свойства ортоцентрических тетраэдров, как будет показано в заключительном пункте этого параграфа, во многом аналогичны соответствующим свойствам треугольников.

Вместе с тем, тетраэдры общего вида также имеют немало свойств, сходных с соответствующими свойствами треугольников. В середине XIX века возникла так называемая многомерная евклидова геометрия. Долгое время геометры, обобщая свойства известных двумерных и трехмерных фигур, вводили и изучали их многомерные аналоги. Различные обобщения по аналогии и сегодня остаются одним из магистральных путей развития математики. Это стало одной из причин того внимания, которое в пособии уделяется аналогиям между свойствами треугольников и тетраэдров.

3.3.2. Связь между замечательными точками треугольника. Рассмотрим известное векторное равенство, связывающее вершины треугольника, его ортоцентр и центр описанной окружности.

Задача 3.10. Докажите, что для произвольного треугольника  имеет место соотношение

,                           (3.33)

где  – его ортоцентр, а  – центр описанной окружности.

Решение. Из условия задачи следует, что ,  

. Перепишем равенства в виде

, .

Скалярное произведение дистрибутивно относительно сложения векторов, поэтому при вычитании этих равенств получим:

.

Аналогично из условий ,  вытекает равенство

.

Вектор , оказался одновременно ортогональным двум неколлинеарным векторам  и . Поэтому этот вектор нулевой, и

. □

Пример 3.3.8. Докажите, что центр  описанной окружности, центроид  и ортоцентр  неравностороннего треугольника принадлежат одной прямой, при этом .

Прямая, на которой лежат точки ,  и , называется прямой Эйлера.

Решение. Из формулы (2.14) имеем: .

Сравнивая вектор  с вектором , видим, что . Перепишем это равенство в виде: . Отсюда , и значит, . □

Пример 3.3.9. Докажите, что точки, симметричные ортоцентру  треугольника  относительно середин его сторон, и точки, симметричные ортоцентру  относительно прямых, содержащих стороны треугольника, принадлежат окружности, описанной около этого треугольника.

Решение. Пусть , ,  – точки, симметричные ортоцентру  треугольника  относительно сторон , ,  соответственно, а , ,  – точки, симметричные  относительно середин этих сторон (рис. 3.31).

Докажем,            например,       что точки ,  принадлежат окружности , описанной около треугольника . Из условия задачи следует, что вектор  лежит на диагонали параллелограмма, построенного на векторах  и     :

                                                                                                  .

Отсюда по определению разности векторов  

 и

где  – центр окружности . Учитывая, что , из полученного равенства заключаем: . Поскольку

, то точка  лежит на окружности .

Докажем, что точка      также принадлежит окружности . Удваивая равенство , в котором  – основание высо-

ты треугольника, опущенной на сторону , а  – середина этой стороны, получим:

.

Поскольку угол  – прямой, угол  также является прямым. Но угол  опирается на диаметр  окружности , поэтому точка  лежит на этой окружности. □

Пример 3.3.10. Докажите, что середины трех сторон, основания трех высот треугольника и середины отрезков, соединяющих ортоцентр с вершинами, принадлежат одной окружности, а центр этой окружности принадлежит прямой Эйлера.

Окружность, о которой говорится в этой задаче, называется окружностью Эйлера или окружностью девяти точек.

Решение. Пусть  – ортоцентр,  – центр окружности , описанной около треугольника . Основания высот, опущенных из вершин , ,  треугольника, обозначим , ,  соответственно, точки, симметричные орто- _H3 центру  относительно сторон

, CA, , – , , , а середины отрезков ,  и  – ,  и  (рис. 3.32).

По условию задачи  

.

A Точки, симметричные ортоцентру треугольника относительно середин

      его сторон, и точки, симметричные                                     2

       ортоцентру относительно прямых,                       Рис. 3.32

содержащих стороны треугольника, принадлежат окружности, описанной около этого треугольника (пример 3.3.9). Поэтому

, , ;

,

где , ,  – точки, симметричные ортоцентру  относительно середин , ,  сторон треугольника .

         На прямой Эйлера выберем точку такую, что

.

Вычитая это соотношение из предыдущих, получим:

, ,

;

, ;

                                                                      ,                       ,

.

Отсюда

                                                        ,                     ,              ;

, , ; , , .

Так        как         

,            то            

. Поэтому точки , , , , , , , ,  принадлежат одной окружности с центром . При этом точка  лежит на прямой Эйлера рассматриваемого треугольника . □

3.2.3. Ортоцентрический тетраэдр. Ортоцентриче-

ский тетраэдр, как уже отмечалось, выделяется среди тетраэдров тем, что его высоты пересекаются в одной точке.

Рассмотрим два признака ортоцентрического тетраэдра. Другие признаки даны в задаче 191 раздела «Задачи для самостоятельного решения».

Задача 3.11. Тетраэдр является ортоцентрическим тогда и только тогда, когда выполнено одно из следующих условий:

(а) две пары его противоположных ребер перпендикулярны (в этом случае третья пара противоположных ребер также перпендикулярна);

(б) отрезки, соединяющие середины противоположных ребер (бимедианы) равны.

Решение. (а) Пусть  – ортоцентрический тетраэдр и  – его ортоцентр. Тогда ,  (рис. 3.33), и значит, векторы ,  перпендикулярны вектору . Поэтому

, .

Вычитая из первого ра- D венства второе, получим:

 

или . Отсюда

       следует,      что .                                                            ^C

Aналогично доказываются равенства ,

        и перпендику-       ^A

       лярность     соответствую-

щих            противоположных      B          Рис. 3.33 ребер.

Обратно, пусть в тетраэдре  перпендикулярны противоположные ребра  и ,  и . Тогда

, .                               (*)

Поэтому

,

и, следовательно, .

Докажем, что прямые, содержащие высоты тетраэдра, пересекаются в одной точке. Проведем через прямую  плоскость , перпендикулярную  (так как , то это возможно). Пусть эта плоскость пересекает  в точке . Высоты  и  тетраэдра лежат в плоскости  и являются высотами треугольника . Обозначим через  точку пересечения этих высот.

Перепишем двумя способами первое из равенств (*):

,  

или

, . Так как            .

Из того, что , имеем: . Но тогда  и

.

:

, .

Как и выше, отсюда получим: , .

Так как  и , то , т. е. точка  ле-

жит на высоте тетраэдра, опущенной из вершины . Аналогично доказывается, что  лежит и на высоте тетраэдра, опущенной из вершины .

(б) В примере 2.2.2 было доказано, что отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаются в одной точке и делятся этой точкой пополам. Сохраним для середин ребер тетраэдра  обозначения, принятые в этом примере: ,  

– середины ребер ,  соответственно; ,  – середины ребер , ; ,  – середины ребер , . Тогда для любой точки :

,

,

Чтобы доказать, что отрезки ,  и  равны, рассмотрим разности квадратов длин этих векторов

  ;

 

В ортоцентрическом тетраэдре, согласно пункту (а), противоположные ребра перпендикулярны, поэтому ,

. Но тогда , и, следовательно, отрезки, соединяющие середины противоположных ребер тетраэдра, равны.

Обратно, если равны отрезки, соединяющие середины противоположных ребер тетраэдра , то равны нулю найденные разности. Откуда следует, что , , и значит,

противоположные ребра тетраэдра перпендикулярны. Поэтому согласно признаку (а) он является ортоцентрическим. □

Задача 3.12. Докажите, что если  – ортоцентр ортоцентрического тетраэдра  и  – центр описанной около него сферы, то

.                   (3.34)

Решение. По условию точка  – центр сферы, описанной около тетраэдра ABCD, поэтому

Точка  – ортоцентр тетраэдра, поэтому , и значит,

           Как    и    в    задаче    3.10,     равенства

, 0 сначала перепишем в виде

, , 

а затем найдем их разность:

                             .

Преобразуем левую часть полученного равенства: 

 

 

Учитывая, что (противоположные ребра ортоцентрического тетраэдра перпендикулярны) и , отсюда имеем:

.

Из соотношений ,  аналогично находим

.

Таким же образом, учитывая, что  и , получим:

.

Из трех найденных равенств следует, что вектор  одновременно ортогонален трем не-

компланарным векторам ,  и . Но это возможно тогда и

только тогда, когда этот вектор нулевой. Поэтому

. □

Докажем, что ортоцентрический тетраэдр обладает свойствами, которые аналогичны свойствам треугольника, рассмотренным в примерах 3.3.8 – 3.3.10.

Пример 3.3.11. Докажите, что центр  описанной сферы, центроид  и ортоцентр  ортоцентрического тетраэдра принадлежат одной прямой (прямая Эйлера^[6] ортоцентрического тетраэдра), при этом точки O и  симметричны относительно точки .

Задача решается аналогично задаче 3.2.2.17)

. Поэтому теперь . Откуда

, и значит, . □

Пример 3.3.12. Точка  – ортоцентр ортоцентрического тетраэдра, точки  и  () – соответственно центроиды и ортоцентры его граней. Докажите, что точки  и  такие, что

, принадлежат сфере, описанной около

этого тетраэдра.

Решение. Пусть  – данный тетраэдр,  – его ортоцентр,  – центр описанной сферы , а  – точка пересечения медиан.

Рассмотрим, например, точки  и , определяемые условиями  соответственно, где точка  –

центроид грани , а  – основание высоты тетраэдра, опущенной на эту грань из вершины . Докажем, что точки  и  принадлежат сфере , описанной около тетраэдра .

Условие, определяющее точку          , перепишем в виде:

.

Отсюда . Но  и для ортоцентрического тетраэдра . Поэтому

.

Из векторного равенства  следует, что .

Следовательно, точка  принадлежит сфере S.

Точка  принадлежит грани , поэтому . Обе части равенства  умножим на 3, а затем воспользуемся условиями задачи:

.

Таким образом,, т. е. угол  равен . Отсюда следует, что точка  принадлежит окружности, для которой отрезок  является диаметром. Но эта окружность является большой окружностью сферы , поэтому

.

Аналогично доказывается, что остальные шесть точек также принадлежат сфере . □

Пример 3.3.13. Докажите, что центроиды четырех граней, основания четырех высот ортоцентрического тетраэдра и точки, которые делят отрезки, соединяющие ортоцентр с вершинами, в отношении , считая от ортоцентра, принадлежат одной сфере, а центр этой сферы принадлежит прямой Эйлера.

Сфера, о которой говорится в этой задаче, называется сферой Эйлера или сферой двенадцати точек.

Решение. Пусть  – ортоцентрический тетраэдр. Для центроидов граней и оснований высот тетраэдра сохраним обозначения предыдущего примера. Точки, которые делят отрезки , ,

, , соединяющие ортоцентр с вершинами, в отношении , считая от ортоцентра, обозначим , , ,  соответственно. Из условий задачи и предыдущего примера:

, , , .

Рассмотрим точку  такую, что

.

Заметим, что эта точка лежит на прямой Эйлера ортоцентрического тетраэдра . Вычитая по частям последнее соотношение из предыдущих, получим:

, ,

                         ,                    ,                 , .

Так как , то  

. Поэтому двенадцать то-

чек – , , , , ,  – принадлежат одной сфере с центром в точке , которая лежит на прямой Эйлера рассматриваемого ортоцентрического тетраэдра. □

3.3.4. Равногранный тетраэдр. Если в треугольнике  какие-либо две из замечательных точек , , ,  совпадают,

то треугольник правильный.

Поэтому естественно предположить, что и тетраэдр, у которого какие-либо две замечательные точки совпадают, также обладает какими-то специфическими свойствами. В произвольном тетраэдре  речь, разумеется, может идти только о совпадении точек ,

 и . Выясним, какими свойствами обладает тетраэдр, у которого

две из этих точек совпадают.

Будем использовать следующие обозначения: , ,

, , , ; , , ,  – площади гра-

ней, противолежащих вершинам , , ,  соответственно

Пример 3.3.14. В тетраэдре  центроид и центр описанной сферы совпадают. Выясните, какими свойствами этот тетраэдр обладает.

Решение. Точка  является центроидом тетраэдра  тогда и только тогда, когда , где  –

произвольная точка. Выберем в качестве точки  точку . По условию точки  и  совпадают, поэтому

.

При этом . Из первого равенства следует,

что и, значит,

или . Откуда

.

Учитывая полученное равенство скалярных произведений, имеем:

, .

Следовательно,  или .

Аналогично доказывается, что

, ,

т. е. , .

Итак, если в тетраэдре центроид и центр описанной сферы совпадают, то его противоположные ребра равны.

Оказывается, имеет место обратное утверждение: если в тетраэдре противоположные ребра равны, то его центроид и центр описанной сферы совпадают.

В самом деле, если , , , то ,

      ,     .      Откуда       ,

 и, следо-

вательно,

, , .

Скалярно умножим вектор  на векторы , ,  и :

,

,

,

.

Отсюда с учетом найденных соотношений между скалярными произведениями имеем:

;

                                                       ,                               ,                               ;

                                                               ,                           , .

Видим, что три некомпланарных вектора ,  и  одновременно ортогональны вектору . Но это возможно лишь при условии, когда вектор  нулевой, т. е. когда .

Таким образом, в тетраэдре  центроид  и центр  описанной сферы совпадают тогда и только тогда, когда длины его противоположных ребер равны. □

Очевидно, что в таком тетраэдре все грани равны по трем сторонам (рис. 3.34).

Тетраэдр, все грани которого равны, называется равногранным. Поэтому полученный результат можно сформулировать следующим образом: в тетраэдре центроид и центр описанной сферы совпадают тогда и только тогда, когда этот тетраэдр является равногранным.

Заметим также, что:

–      разверткой равногранного тетраэдра  является треугольник , отрезки , ,  в котором являются средними линиями (рис. 3.35);

–      сумма плоских углов при каждой вершине равногранного тетраэдра равна ;

–      все его грани – остроугольные треугольники.

Пример 3.3.15. В тетраэдре центры описанной и вписанной сфер совпадают. Выясните, какими свойствами этот тетраэдр обладает.

Решение. Пусть центр  описанной сферы тетраэдра  

совпадает с центром  вписанной. Тогда плоскости всех граней тетраэдра одинаково удалены от общего центра сфер. Поэтому окружности, по которым грани пересекают описанную сферу, равны. Используя это свойство тетраэдра, можно, не прибегая к векторам, провести следующие рассуждения.

В равных окружностях равные хорды стягивают равные дуги, а углы, опирающиеся на равные дуги, равны. Поэтому у любых двух граней тетраэдра плоские углы, лежащие против их общего ребра, равны (рис. 3.36). Пусть

, , ,

, , .

Тогда в треугольниках , , ,  соответственно:

             

,            , ,        .

D

Рис. 3.36 Сравнивая первое равенство с третьим, а второе с четвертым, получим

,  

Отсюда следует, что

, , .

Таким образом, каждые два из рассматриваемых треугольников имеют общую сторону и соответственные углы в этих треугольниках, прилежащие к общей стороне, равны. Поэтому все они равны между собой. Это означает, что тетраэдр  опять является равногранным.

Докажем обратное утверждение, т. е. установим, что в любом равногранном тетраэдре центры описанной и вписанной сфер совпадают. В равногранном тетраэдре  площади всех граней равны, поэтому из формулы (3.32) имеем:

                                              .

Следовательно, центр  сферы, вписанной в тетраэдр, находится в его центроиде . Но согласно задаче 3.3.14, в любом равногранном тетраэдре центроид и центр описанной сферы совпадают. □

Из задач 3.3.14, 3.3.15 вытекает, что центроид тетраэдра и центр вписанной в него сферы совпадают тогда и только тогда, когда этот тетраэдр равногранный.

При решении задач, в которых встречаются равногранные тетраэдры, полезно знать следующий признак.

Пример 3.3.16. Докажите, что тетраэдр является равногранным тогда и только тогда, когда прямые, содержащие его бимедианы, попарно перпендикулярны.

Решение. Пусть  – равногранный тетраэдр;  и  – середины ребер  и ;  и  – середины ребер  и ;  и  – середины ребер  и . Тогда

,

где  – произвольная точка. Откуда

.

Аналогично находим:

.

Докажем, что , , . В равногранном тетраэдре, как следует из примера 3.2.14,

, ,  

и, следовательно,

                                                                      ,                        ,

.

Откуда

, ,

;

,

,

.

и, значит,

.

Таким образом, прямые, содержащие бимедианы равногранного тетраэдра , попарно перпендикулярны.

Чтобы доказать обратное утверждение, достаточно обратить проведенные рассуждения. □

Напомним, что если через каждое ребро тетраэдра провести плоскость, параллельную противоположному ребру, то эти шесть плоскостей высекают параллелепипед, который обычно называют описанным параллелепипедом данного тетраэдра. Ребра тетраэдра для этого параллелепипеда служат диагоналями граней. Легко доказать, что описанный параллелепипед равногранного тетраэдра является прямоугольным (рис. 3.37). При этом бимедианы тетраэдра равны и параллельны ребрам параллелепипеда. Поэтому прием достраивания тетраэдра до параллелепипеда при решении задач на равногранный тетраэдр используется наиболее часто и весьма эффективно.

Пример 3.3.17. В тетраэдре противоположные ребра равны и имеют длины ,  и . Найдите объем тетраэдра и радиуса описанной и вписанной сфер.

Решение. Противоположные ребра тетраэдра равны, поэтому он равногранный. Достроим тетраэдр до параллелепипеда и обозначим ребра последнего через ,  и  (рис. 3.37). По теорема Пифагора

,

, .

Откуда и

.

Искомый объем  тетраэдра будет равен разности между объемом параллелепипеда и учетверенным объемов прямоугольного тетраэдра, в котором ребра, образующие прямой трехгранный угол, равны ребрам параллелепипеда, т. е. . По-

этому и

.

Диагонали прямоугольного параллелепипеда равны и точкой их пересечения делятся пополам. Поэтому сфера, описанная около тетраэдра, будет описана и около параллелепипеда, при этом диаметр сферы будет равен половине диагонали параллелепипеда, т. е. .

Площадь  грани тетраэдра может быть найдена по формуле Герона:

.

Площади всех граней тетраэдра равны между собой, поэтому радиус вписанной сферы тетраэдра

. □

При решении «задач на равногранный тетраэдр» кроме достраивания его до прямоугольного параллелепипеда столь же эффективен прием достраивания равногранного тетраэдра до прямоугольного (см. задачи 198, 199).

Наконец, пусть равногранный тетраэдр является ортоцентрическим. В таком тетраэдре противоположные ребра равны и перпендикулярны. Следовательно, его описанный параллелепипед – куб, а сам тетраэдр является правильным. В правильном тетраэдре все четыре точки , ,  и  совпадают.

 

Задачи для самостоятельного решения

 

Во всех задачах, в формулировках которых дан треугольник

, без дополнительных оговорок считается: , ,  площадь; ,  – радиусы описанной

и вписанной окружностей, ,  – их центры;  – ортоцентр. Так же точно, в задачах, в формулировках которых дан тетраэдр , приняты обозначения: , , , , ,

; , , ,  – площади граней, противолежащих вершинам , , ,  соответственно;  – объем тетраэдра;  и  (3,4) – высоты и медианы тетраэдра, проведенные из вершин , , ,  соответственно; ,  – радиусы описанной и вписанной сфер, ,  – их центры.

154.     Докажите, что

,

где , ,  – биссектрисы треугольника .

155.     Докажите, что

,

где , ,  – высоты треугольника .

156.     Докажите следующие формулы для вычисления площади треугольника :

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) ;

з) ;

и) ;

к) ;

л) .

157.        Докажите, что для любой точки  радиус-вектор  центра  описанной около треугольника  окружности можно представить в виде:

,

где , ,  – площади треугольников , ,  соответственно.

158.        Докажите, что для любого треугольника :

а) ;

б) ,

;

в) ;

г) ,

,

где , ,  – радиусы вневписанных окружностей.

159.        Докажите следующие формулы для вычисления объема тетраэдра :

а)  – угол наклона ребра  к плоскости ;

б) ;

в) ;

г) ;

д) ;

е) , где  – площадь треугольника, стороны которого

численно равны , ,  (формула Крелле^[7]).

160.        Плоские углы при одной вершине тетраэдра прямые.

Площади граней, инцидентные этой вершине, равны , , .

Найдите объем тетраэдра.

161.        Выразите объем тетраэдра через длины его ребер.

162.        Докажите, что, сумма векторов внешних нормалей плоскостей граней тетраэдра, длины которых равны площадям соответствующих граней, равна нулевому вектору.

163                      (теорема косинусов для тетраэдра). Докажите, что квадрат площади любой грани тетраэдра равен сумме квадратов площадей трех остальных граней без удвоенных произведений площадей этих граней, взятых попарно, и косинусов двугранных углов между ними. Например,

,

где , ,  – косинусы двугранных углов при ребрах , ,  соответственно.

164                      (теорема синусов для тетраэдра). Докажите, что отношение произведения длин двух противоположных ребер тетраэдра к произведению синусов двугранных углов при этих ребрах одно и то же для всех трех пар противоположных ребер:

.

165                      (теорема тангенсов для тетраэдра). Дан тетраэдр

. Докажите, что

 .

166.          Дан прямоугольный треугольник  с прямым углом . Точка  – основание высоты, опущенной из вершины прямого уг-

ла. Разложите вектор  по векторам  и , если ,

.

167.          Дан прямоугольный тетраэдр  с прямыми плоскими углами при вершине . Точка  – основание высоты, опущенной из вершины  на плоскость грани . Разложите вектор  по векторам ,  и , если , , .

168.          В тетраэдре  все плоские углы при вершине  прямые. Докажите, что основание высоты, опущенной из вершины  на грань  – точка пересечения высот треугольника .

169.          В тетраэдре  все плоские углы при вершине  прямые. Докажите, что радиус вписанной в тетраэдр сферы определяется формулой

.

170.          В тетраэдре  все плоские углы при вершине  прямые. Докажите, что радиус сферы, описанной около тетраэдра, определяется формулой

.

171.          В тетраэдре  все плоские углы при вершине  пря-

мые; длина высоты  . Докажите, что

.

172.          В правильной треугольной пирамиде ребро основания равно , боковое ребро – . Найдите радиус сферы, описанной около тетраэдра.

173.          Две грани тетраэдра – равносторонние треугольники со стороной 1, две другие – равнобедренные прямоугольные треугольники. Найдите радиус сферы, вписанной в тетраэдр.

174.          Даны длины всех сторон треугольника . Найдите длину  медианы  этого треугольника.

175.          Даны длины всех ребер тетраэдра . Найдите длину  медианы  этого тетраэдра.

176.          Докажите, что в любом треугольнике :

а) ;

б) .

177.          Докажите, что в любом тетраэдре :

а) ;

.

178.          Докажите, что расстояние от центра  окружности, описанной около треугольника , до его центроида  определяется формулой

.

179.          Докажите, что расстояние от центра  сферы, описанной около тетраэдра , до его центроида  определяется формулой

.

180.          Докажите, что в любом треугольнике  

.

181.          Докажите, что в любом тетраэдре  

.

182.          Докажите, что для любого треугольника  справедливо соотношение

,

где , ,  – радиусы вневписанных окружностей.

183.          Докажите, что для любого тетраэдра  справедливо соотношение

,

где , , ,  – радиусы сфер, каждая из которых касается одной из его граней и продолжений трех остальных (вневписанные сферы тетраэдра).

184.          Докажите, что для любого треугольника  и произвольной точки  имеет место соотношение

 

(формула Лейбница^[8] для треугольника).

             

185.          Докажите, что для любого тетраэдра  и произвольной точки  имеет место соотношение

 

(формула Лейбница для тетраэдра).

186.          Докажите, что угол  между двумя противоположными ребрами любого тетраэдра  определяется формулой

.

187.          Даны длины всех ребер тетраэдра . Найдите длины его бимедиан.

188.          Докажите, что сумма квадратов длин бимедиан тетраэдра равна .

189.          Через середину каждого ребра тетраэдра проведена плоскость, перпендикулярная противоположному ребру. Докажите, что все эти шесть плоскостей пересекаются в одной точке (точка Монжа).

190.          Через каждое ребро тетраэдра и середину противоположного ему ребра проведена плоскость. Докажите, что все эти шесть плоскостей пересекаются в одной точке.

191.          Докажите, что тетраэдр является ортоцентрическим тогда и только тогда, когда выполнено одно из следующих условий:

а) суммы квадратов противоположных ребер равны;

б) основанием одной из высот тетраэдра является ортоцентр

противоположной грани;

в) произведения косинусов противоположных двугранных уг-

лов равны.

192.          Докажите, что плоские углы при каждой вершине ортоцентрического тетраэдра либо все острые, либо все прямые, либо все тупые.

193.          Докажите, что если в ортоцентрическом тетраэдре одна из граней является правильным треугольником, то ребра, прилежащие к противоположной ей вершине, равны между собой.

194.          Докажите, что в ортоцентрическом тетраэдре точка Монжа совпадает с центроидом.

195.          Докажите, что для любого треугольника  справедливо соотношение

.

196.          Докажите, что для любого ортоцентрического тетраэдра  справедливо соотношение

.

197.          Докажите, что для любого треугольника  справедливо соотношение

.

198.          Докажите, что для любого ортоцентрического тетраэдра  справедливо соотношение

,

где  – длина его бимедианы.

199.          В прямоугольном тетраэдре  с прямым трехгранным углом при вершине  проведены медианы , ,  граней.

Докажите, что тетраэдр  равногранный.

200.          Докажите, что любой равногранный тетраэдр можно вписать в прямоугольную треугольную пирамиду так, чтобы одна вершина тетраэдра совпадала с вершиной пирамиды, а остальные вершины тетраэдра принадлежали сторонам основания пирамиды.

201.          Докажите, что тетраэдр является равногранным тогда и только тогда, когда его грани равновелики.

202.          Определите вид тетраэдра, все четыре медианы которого равны между собой.

203.          Определите вид тетраэдра, все четыре высоты которого равны между собой.

 

Ответы, указания, решения

 

§ 2.2

,

.        .       .

.

§ 2.3

. Указание: Из соотношений ,

, где  – про-

извольная точка, следует, что   Воспользоваться формулой 2.17 и результатом

примера 2.2.2.

§ 2.4

59. , считая от вершины . 60. Указание: Применить теорему Менелая сначала к треугольнику  и точкам , ,    прямой ,  а затем треугольнику  и точкам , ,  прямой .

61. , считая от точки . 64. Указание: Последовательно применить теорему Менелая к треугольнику и прямым , ,  

(рис. 1): , ,

. Перемножить эти равенства и учесть, Указание: Использовать теорему Менелая в тригонометрической форме. 67. Указание: Доказать, что ,  

,                                           (рис.

2)а) Пусть , ,  – со-

ответственно длины сторон , ,  треугольника ,  и каждая из прямых , ,  делит периметр  

треугольника пополам. Тогда, например,  и

. Аналогично находятся , , ,

, . б) Прямые , ,  совпадают с од-

ноименными прямыми из задачи а). Рассмотрим, например, окружность, вневписанную в угол  треугольника . Пусть она касается прямых , ,  в точках , ,  (рис. 3). По свойству касательной к окружности

, , . Отсюда следует, что                 

                                                 

, , 

, . 71. Указание: В общем случае (рис. 2.31) примените прямую теорему Дезарга к треугольникам , .

.

75. Указание: Использовать результаты задач 73, 74. 76. Указание: Использовать стереометрический аналог теоремы Менелая и идею решения задачи 2.4.7, в). . Указание: Пусть ,

,  – биссектрисы углов треугольника ; , ,  – длины сторон , , ;  – центр вписанной окружности. Тогда  и по теореме Ван-Обеля  Указание:

Пусть , , . С помощью теоремы Ван-Обеля выразите отношения , ,  через , ,  и учтите, что по теореме Чевы .

§ 3.1

79. Указание: Пусть  – данный треугольник, ; тогда  

Пусть  – трапеция с основа-

ниями  и  тогда . Равенство следует из тождества  (задача 3.1).

90. Указание: Использовать равенство  и тео-

рему косинусов. 91. Указание: Пусть  – центроид тетраэдра ,

тогда  (см. формулу (2.18)). Отсюда с использованием теоремы косинусов получим

.

92. а) Указание: Использовать равенство   и теорему косинусов при вычислении  и

. б) Доказать, что , при вычислении длины этого вектора применить теорему косинусов. .

 .

, если , если

 для граней с общим реб-

ром  для граней с общим ребром ,

 для граней с общим ребром . 104.  

.

§ 3.2

 .

124. Указание: Пусть – единичные направляющие векторы ребер ,  и . Тогда векторы направляющие векторы биссектрис углов , , а вектор  – направляющий вектор биссектрисы угла, смежного с углом .

При этом  

Указание: Рассмотреть высоты треугольника, являющегося сечением трехгранного угла плоскостью, проходящей перпендикулярно общему ребру непрямых плоских углов. 128. Указание:  

 – еди-

ничные направляющие векторы ребер ,  и  трехгранного угла. 130, 131. Указание: Использовать первую и вторую теорему косинусов для трехгранного угла. 132. Указание: Из первой теоремы косинусов для трехгранного угла следует, что

, где . Из усло-

вий задачи , ,   а, значит,  

и . 133. Указание: Воспользоваться второй теоремой косинусов для трехгранного угла. 134. Указание: Воспользоваться методом от противного. 135. Указание: См. пример 3.2.8 а). 136.

 . 137.  . 138.  . . 141.

. ;

г) ; д) ; е)  

 Указание: ,

где  

.

§ 3.3

154, 155. Указание: Воспользоваться результатом задачи 3.3.

Указание: См. предыдущую задачу.           ,

 Указа-

ние: г) Рассмотреть параллелепипед, образованный плоскостями, проходящими через ребра тетраэдра параллельно противоположным ребрам. е) См. формулу (3.30).  Воспользоваться результатом примера 3.26 и теоремой косинусов для треугольника. 162. Решение: Пусть  – данный тетраэдр. Площади граней , , ,  тетраэдра обозначим , ,,

соответственно. Возьмем произвольную внутреннюю точку  тетраэдра и разобьем тетраэдр на четыре треугольные пирамиды с общей вершиной , основаниями которых являются грани данного тетраэдра. Высоты пирамид, проведенные из вершины , обозначим . Объем  тетраэдра  равен сумме объемов этих пирамид: . Пусть  – единичный вектор внешней нормали грани c площадью произвольная точка этой грани. Тогда  

      .     Отсюда   следует,   что       

. Рассмотрим любую внутреннюю точ-

         ку  тетраэдра, отличную от                                           и

 

 

 

.

       Очевидно,         что                                                                       

. Поэтому  

для любого вектора . Но это возможно лишь тогда, когда

. 163. Указание: Воспользоваться

результатом предыдущей задачи. Так как  

. Указание: Соглас-

но 159 г) . Отсюда   и, следовательно,  

. Решение: Пусть  – основание высоты тетраэдра , опущенной из вершины . Разобьем треугольник  на треугольники , ,  и вычислим их высоты, опущенные на стороны , ,  соответственно. Тогда для площади  грани  имеем:.

Откуда

.

Аналогично ищутся соотношения:

,

, .

Вычтем по частям из суммы первого и четвертого соотношений сумму второго и третьего:

.

Возведя это соотношение в квадрат, а затем выполнив замены

, с учетом равенств

) получим:

 

Справедливость доказываемых равенств следует из симметрии выражения, стоящего в правой части найденного соотношения.

. Указание: , где .

По     условию .

 

 

. 176. Указание: Воспользоваться результатом задачи 174. 177. Указание: Воспользоваться результатом задачи 17     . Указание:

Воспользоваться равенством . Указание: Воспользоваться равенством .

180. Указание: Воспользоваться формулами  . Воспользоваться формулами  

. Указание: Сначала дока-

жите, что . 183. Указание:

Пусть  – центр,  – радиус сферы, касающейся грани, площадь которой равна  (), и продолжений трех остальных граней.          Тогда   ,       откуда  

. С другой стороны, . Указание:

Положим ,

      .     Доказать,         что  

, где  –

середина ребра ,  – середина ребра . Указание: Положим

, , ; тогда . Отсюда

 

Длины двух других бимедиан ищутся аналогично. 189. Решение. Пусть дан тетраэдр ,  – середина ребра ,  – середина ребра ,  – центроид тетраэдра,  – центр описанной около него сферы. Тогда  (центр  – точка пересечения плоскостей, проходящих через середины ребер перпендикулярно к этим ребрам);  – середина бимедианы  (см. задачу 58). Пусть точка  симметрична точке  относительно точки . Тогда . Отсюда следует, что прямая  перпендикулярна ребру , и, следовательно, точка  принадлежит плоскости, проходящей через точку  перпендикулярно ребру . Аналогичные рассуждения для ос-

тальных пар противоположных ребер позволяют заключить, что точка  принадлежит каждой из шести плоскостей, проходящих через середины ребер тетраэдра перпендикулярно противоположным ребрам. Примечание: Приняв центр  чало векторов, можно доказать, что .

190. Указание: Плоскости пересекаются в центроиде тетраэдра. 191. а) Решение: Пусть в тетраэдре  суммы квадратов противоположных ребер равны, т.е.  

. В силу тождества б) задачи 3.1 имеют место равенства:

 

. Поэтому , , и согласно задаче

3.11 тетраэдр  является ортоцентрическим. б) Указание:

. Тогда , откуда  и . Поэтому  тогда и только тогда, когда . в) Указание: Воспользоваться теоремами тангенсов и синусов для тетраэдра. 192. Указание: В ортоцентрическом тетраэдре  в силу 191 а):  

.        Откуда  

,                           и

,               

. Следовательно, либо углы , ,

 прямые, либо их косинусы имеют один знак. 193. Указание: Использовать результат задачи 191 б). 195. Указание: В формуле

задачи 178 учесть, что . Указание: В формуле задачи 179 учесть, что , и при этом  

. 197. Указание: Из (3.33), используя теорему косинусов,       имеем:              

 

. 198. Указание:

Учесть, что в ортоцентрическом тетраэдре  

. Указание: Достроить тетраэдр до

параллелепипеда и доказать, что этот параллелепипед прямоугольный. При доказательстве учесть, что высоты смежных граней тетраэдра, опущенные на их общее ребро, равны. 202. Равногранный тетраэдр. 203. Равногранный тетраэдр.

 

Список использованной и рекомендуемой литературы

 

1.    Атанасян Л.С., Базылев В.Т. Геометрия. В 2-х ч. Ч. I. Учебное пособие для студентов физ.-мат. фак. пед. ин-тов. – М.: Просвещение, 1986. – 336 с.

2.    Болтянский В.Г. Элементарная геометрия: Кн. для учителя. – М.: Просвещение, 1985. – 320 с.

3.    Габович И.Г. Алгоритмический подход к решению геометрических задач: Книга для учащихся. – М.: Просвещение: АО «Учебная литература», 1996. – 192 с.

4.    Готман Э.Г., Скопец З.А. Задача одна – решения разные: Геометрические задачи: Книга для учащихся. – М.: Просвещение, 2000. – 224 с.

5.    Готман Э.Г., Скопец З.А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9 и 10 классов. – М.: Просвещение, 1979. – 128 с.

6.    Дубнов Я.С. Основы векторного исчисления. Ч. I. – M.-Л.: Гостехиздат, 1950. – 368 с. 7. Клопский В.М., Скопец З.А., Ягодовский М.И. Геометрия: Учебное пособие для 9-10 классов. – М.: Просвещение, 1982. – 256 с.

8.                   Майоров В.М., Скопец З.А. Векторное решение геометрических задач (задачник-практикум по спецсеминару). – М.: Просвещение, 1968. – 252 с.

9.                   Моденов П.С. Задачи по геометрии. – М.: Наука. Гл. ред. физ.мат. лит., 1979. – 368 с.

10.               Понарин Я.П. Элементарная геометрия: В 2-х т. – Т. 1: Планиметрия, преобразования плоскости. – М.: МЦНМО, 2004. – 332 с.

11.               Прасолов В.В. Задачи по планиметрии. Ч. 1. – 2-е изд., перераб. и доп. – М.: Наука. Гл. ред. физ.-мат. лит., 1991. – 320 с. – (Б-ка мат. кружка. Вып. 15).

12.               Прасолов В.В. Задачи по планиметрии. Ч. 2. – 2-е изд., перераб. и доп. – М.: Наука. Гл. ред. физ.-мат. лит., 1991. – 240 с. – (Б-ка мат. кружка).

13.               Прасолов В.В., Шарыгин И.Ф. Задачи по стереометрии. – М.: Наука. Гл. ред. физ.-мат. лит., 1989. – 288 с. – (Б-ка мат. кружка).

14.               Шарыгин И.Ф. Задачи по геометрии (планиметрия). – М.: Наука. Гл. ред. физ.-мат. лит., 1982. – 160 с. – (Библиотечка «Квант». Вып. 17).

15.               Шарыгин И.Ф. Задачи по геометрии (стереометрия). – М.: Наука. Гл. ред. физ.-мат. лит., 1984. – 160 с. – (Библиотечка «Квант». Вып. 32).

16.               Шарыгин И.Ф., Гордин Р.К. Сборник задач по геометрии. 5000 задач с ответами. – М.: ООО «Изд-во Астрель», 2001. – 400 с.

17.               Шестаков С.А. Векторы на экзаменах. Векторный метод в стереометрии. – М.: МЦНМО, 2005. – 112 с.

18.               Шклярский Д.Ю., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики. Геометрия (планиметрия). – 3-е изд. – М.: ФИЗМАТЛИТ, 2000. – 336 с.

19.               Шклярский Д.Ю., Ченцов Н.Н., Яглом И.М. Избранные задачи и теоремы элементарной математики. Геометрия (стереометрия). – 3-е изд. – М.: ФИЗМАТЛИТ, 2000. – 280 с.

        

Учебное издание

 

 

 

 

 

КЛЕКОВКИН ГЕННАДИЙ АНАТОЛЬЕВИЧ

 

Решение геометрических задач векторным методом

 

Учебное пособие для учащихся 10-11 классов

 

 

 

 

 

 

Компьютерная верстка Г.А. Клековкин

Корректура Н.В. Мыльникова

Обложка 

 

 

 

Самарский филиал ГАОУ ВО города Москвы «Московский городской педагогический университет», 443041, г. Самара, ул. Братьев Коростелевых, 76.

 

Подписано в печать . Формат . Бумага офисная.

Гарнитура Times New Roman. Печать оперативная. Усл. печ. л. 11,25.

Тираж 100 экз. Заказ .