РП по предмету "Алгебра и начала математического анализа" 11 класс.

 

Муниципальное общеобразовательное автономное учреждение

средняя общеобразовательная школа № 6

городского округа город Нефтекамск Республики Башкортостан

 

 

РАССМОТРЕНО на заседании ШМО руководитель ШМО ___________ Ижбулдина Е.С. Протокол № ______ от «___» _________ 2019г.

СОГЛАСОВАНО Зам. директора по УР _______ С.Ю. Лепаева Пр. МС № _________ от «___» _______ 2019 г.

УТВЕРЖДАЮ Директор МОАУ СОШ №6 ____________ Л.Ю. Гайсина «___» _________ 2019г. Приказ №______ от _______

 

 

 

 

 

 

 

 

 

 

 

 

РАБОЧАЯ ПРОГРАММА

по   предмету «Алгебра и начала математического анализа»

 11 класс

 

 

 

 

 

 

 

 

 

 

Учитель: Гребенкина И.В.

 

 

 

 

 

 

 

 

 

Нефтекамск 2019 г

 

 

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Рабочая программа по алгебре и началам математического анализа составлена на основании следующих документов:

              1)Федеральный Закон «Об образовании в Российской Федерации» от 29.12.2012 года №273;

               2) Федерального компонента Государственных образовательных стандартов основного общего образования (приказ Министерства образования РФ от 05.03.2004г. №1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего(полного) общего образования);

                           3) примерной программы среднего общего образования по алгебре и началам математического анализа;

                           4) авторской рабочей программы Математика: алгебра и начала анализа 10-11 класс общеобразовательных школ (М.:«Дрофа», 2013) Г. К. Муравин, О. В. Муравина учебника «Алгебра и начала математического анализа 10 класс». Углубленный уровень (М.:«Дрофа»,2014);

                          5)Приказа Министерства образования и науки Российской Федерации № 253 от 31.03.2014 «Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию»;

                          6) Федеральный базисный учебный план, утвержденный приказом Минобразования России от 09.03.2004 № 1312.

 

                          7) учебного плана МОАУ СОШ № 6 городского округа г. Нефтекамск РБ на 2019-2020 учебный год.

Углубленный курс математики ориентирован на учащихся, которые собираются продолжать изучение математики в высших учебных заведениях.

Изучение алгебры и начал математического анализа  на ступени среднего общего образования направлено на достижение следующих целей:

развитие личности школьника средствами математики, подготовка его к продолжению обучения и к самореализации в современном обществе.

 Достижение перечисленных целей предполагает решение следующих задач:

 — формирование мотивации изучения математики, готовности и способности учащихся к саморазвитию, личностному самоопределению, построению индивидуальной траектории в изучении предмета;

 — формирование у учащихся способности к организации своей учебной деятельности посредством освоения личностных, познавательных, регулятивных и коммуникативных универсальных учебных действий;

 — формирование специфических для математики стилей мышления, необходимых для полноценного функционирования в современном обществе, в частности логического, алгоритмического и эвристического;

 — освоение в ходе изучения математики специфических видов деятельности, таких как построение математических моделей, выполнение инструментальных вычислений, овладение символическим языком предмета и др.;

 — формирование умений представлять информацию в зависимости от поставленных задач в виде таблицы, схемы, графика, диаграммы, использовать компьютерные программы, Интернет при ее обработке;

 — овладение учащимися математическим языком и аппаратом как средством описания и исследования явлений окружающего мира;

 — овладение системой математических знаний, умений и навыков, необходимых для решения задач повседневной жизни, изучения смежных дисциплин и продолжения образования;

 — формирование научного мировоззрения;

 — воспитание отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

 

Согласно учебного  плана МОАУ СОШ № 6 ГО г. Нефтекамск РБ на  изучение предмета алгебра и начала математического анализа (среднее общее образование) отводится:

165 часов из расчета 5 часа в неделю.

 

 Требования к уровню подготовки обучающихся (выпускников):

сформированность:

— целостного мировоззрения, соответствующего современному уровню развития науки математики и общественной практики ее применения;

 — основ саморазвития и самовоспитания в соответствии с общечеловеческими ценностями и идеалами гражданского общества; готовности и способности к самостоятельной, творческой и ответственной деятельности с применением методов математики;

 — готовности и способности к образованию, в том числе самообразованию, на протяжении всей жизни; сознательного отношения к непрерывному образованию как условию успешной профессиональной и общественной деятельности на основе развитой мотивации учебной деятельности и личностного смысла изучения математики, заинтересованности в приобретении и расширении математических знаний и способов действий, осознанности в построении индивидуальной образовательной траектории;

 — осознанного выбора будущей профессии, ориентированной в применении математических методов и возможностей реализации собственных жизненных планов; отношения к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;

— логического мышления: критичности (умение распознавать логически некорректные высказывания), креативности (собственная аргументация, опровержения, постановка задач, формулировка проблем, работа над исследовательским проектом и др.); — способности самостоятельно ставить цели учебной и исследовательской, проектной деятельности, планировать, осуществлять, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями ее выполнения;

— умения самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;

 — умения находить необходимую информацию, критически оценивать и интерпретировать информацию в различных источниках (в справочниках, литературе, Интернете), представлять информацию в различной форме (словесной, табличной, графической, символической), обрабатывать, хранить и передавать информацию в соответствии с познавательными или коммуникативными задачами;

 — навыков осуществления познавательной, учебно-исследовательской и проектной деятельности, навыков разрешения проблем; способности и готовности к самостоятельному поиску методов решения практических задач, применению различных методов познания;

 — умения продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;

 — владения языковыми средствами

 — умения ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

 — владения навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения.

— представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;

 — представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

— умений применения методов доказательств и алгоритмов решения; умения их применять, проводить доказательные рассуждения в ходе решения задач;

— стандартных приемов решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использования готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;

— умения обосновывать необходимость расширения числовых множеств (целые, рациональные, действительные, комплексные числа) в связи с развитием алгебры (решение уравнений, основная теорема алгебры);

— умений описывать круг математических задач, для решения которых требуется введение новых понятий (степень, арифметический корень, логарифм; синус, косинус, тангенс, котангенс; арксинус, арккосинус, арктангенс, арккотангенс); решать практические расчетные задачи из окружающего мира, включая задачи по социально-экономической тематике, а также из смежных дисциплин;

 — умений приводить примеры реальных явлений (процессов), количественные характеристики которых описываются с помощью функций; использовать готовые компьютерные программы для иллюстрации зависимостей; описывать свойства функций с опорой на их графики; соотносить реальные зависимости из окружающей жизни и из смежных дисциплин с элементарными функциями, делать выводы о свойствах таких зависимостей;

— умений объяснять на примерах суть методов математического анализа для исследования функций и вычисления площадей фигур, ограниченных графиками функций; объяснять геометрический и физический смысл производной; пользоваться понятием производной при описании свойств функций;

 — представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;

 — навыков использования готовых компьютерных программ при решении задач;

               — представлений о необходимости доказательств при обосновании математических утверждений;

— понятийного аппарата по основным разделам курса математики; знаний основных теорем, формул и умения их применять; умения доказывать теоремы и находить нестандартные способы решения задач;

— умений моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат;

— представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;

— умений составления вероятностных моделей по условию задачи и вычисления вероятности наступления событий, в том числе с применением формул комбинаторики и основных теорем теории вероятностей; исследования случайных величин по их распределению.

 

 

 

Содержание учебного материала

 

ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ. 17 часов.

Понятие о непрерывности функции. Теорема о промежуточном значении функции. Понятие о пределе функции. Предел функции в точке и на бесконечности. Односторонние пределы. Связь между существованием предела и непрерывностью функции. Предел суммы, произведения и частного функций. Горизонтальные, вертикальные и наклонные асимптоты.

 

 ПРОИЗВОДНАЯ. 49 часов

Понятие о касательной к графику функции. Уравнение касательной. Определение производной. Геометрический и физический смыслы производной. Производная степенной функции. Метод математической индукции. Производные суммы, разности, произведения и частного функций. Производные основных элементарных функций. Производная сложной функции. Производная неявной функции. Производная обратной функции. Вторая производная, ее геометрический и физический смысл. Теорема Лагранжа. Применение первой и второй производных к исследованию функции и построению ее графика. Дифференциальное уравнение гармонических колебаний. Использование производной при решении уравнений и неравенств. Решение текстовых задач на нахождение наибольших и наименьших значений.

 

ИНТЕГРАЛ. 14 часов.

Площадь криволинейной трапеции. Интеграл как предел суммы. Первообразная. Первообразные основных элементарных функций. Правила вычисления первообразных. Формула Ньютона—Лейбница. Примеры применения интеграла в физике и геометрии.

 

УРАВНЕНИЯ И НЕРАВЕНСТВА. 28 часов.

 Решение рациональных, иррациональных, показательных, логарифмических, тригонометрических уравнений и неравенств, а также их систем. Основные приемы решения систем уравнений: подстановка, сложение, введение новых переменных, умножение и деление одного уравнения системы на другое. Равносильность уравнений, неравенств и их систем. Решение систем уравнений с двумя неизвестными. Решение систем неравенств с одной неизвестной. Уравнения, неравенства и их системы с параметрами. Доказательство неравенства, в том числе с помощью метода математической индукции. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений, неравенств с двумя переменными и их систем. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.

 

 

ВЕРОЯТНОСТЬ И СТАТИСТИКА. 12 часов.

Представление данных, их числовые характеристики. Таблицы и диаграммы. Случайный выбор. Интерпретация статистических данных и их характеристик. Случайное событие и вероятность. Вычисление вероятностей. Перебор вариантов и элементы комбинаторики (формулы числа перестановок, размещений и сочетаний элементов). Испытания Бернулли. Случайные величины и их характеристики. Частота и вероятность. Закон больших чисел. Оценка вероятностей наступления событий в простейших практических ситуациях.

 

КОМПЛЕКСНЫЕ ЧИСЛА. 18 часов.

Комплексные числа. Алгебраическая, геометрическая и тригонометрическая формы комплексных чисел. Действительная и мнимая часть, модуль и аргумент комплексного числа. Сопряженные и равные комплексные числа. Арифметические действия над комплексными числами в разных формах записи. Возведение в натуральную степень комплексного числа (формула Муавра). Основная теорема алгебры (без доказательства).

 

 

 

 

ТЕМАТИЧЕСКИЙ ПЛАН

 

№ п/п	Тема	Количество часов, отведенных на изучение темы	Количество контрольных работ
1	Непрерывность и пределы функции.	17	1
2	Производная функции.	18	1
3	Техника дифференцирования.	31	1
4	Интеграл и первообразная.	14	1
5	Уравнения, неравенства и их системы.	28	1
6	Элементы теории вероятностей и статистики.	12	1
7	Комплексные числа.	18	1
8	Повторение.	27	1
Итого:		165	8

 

 

 

 

В рабочую программу внесены следующие изменения:

 

            Авторская рабочая программа Математика: алгебра и начала анализа 10-11 класс общеобразовательных школ (М.:«Дрофа», 2013) Г. К. Муравин, О. В. Муравина учебника «Алгебра и начала математического анализа 10 класс». Углубленный уровень (М.:«Дрофа»,2014) рассчитана  на 136  часов, данная рабочая программа рассчитана на 33 учебные недели, по 5 учебных часа в неделю, всего  165  часов.

            В связи с этим равномерно увеличено количество часов исходя из объема изучаемого материала. 

 

 

 

 

Учебно-методическое обеспечение

 

 

• Муравина О. В. Рабочая программа. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10—11 классы
• Муравин Г. К., Муравина О. В. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. Углубленный уровень.11 класс.

• Звавич Л. И., Рязановский А. Р. Алгебра в таблицах.7—11 классы. Справочное пособие.
• Математика в формулах. 5—11 классы. Справочное пособие. Беляева Э. С., Потапов А. С., Титоренко С. А.
• Уравнения и неравенства с параметром. Учебный комплект в 2 ч. c мультимедийным приложением. (Выпускной/Вступительный экзамен).
• Богомолов Н. В. Математика. Задачи с решениями. Учебное пособие.
• Черкасов О.Ю., Якушев А. Г. Математика. Учебное пособие.
• Петров В. А. Математика. 5—11 классы. Прикладные Задачи
• Методическое пособие к учебнику «Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. Углубленный уровень. 11 класс» Муравин Г. К., Муравина О.

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 

к рабочей программе

среднего общего образования

по алгебре и началам математического анализа

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Контрольно – измерительные материалы

к контрольным работам по алгебре и началам математического анализа

для 11 класса

на 2019 – 2020 учебный год

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Учитель:

Гребенкина И.В.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Контрольная работа № 6

по теме «Уравнения, неравенства и их системы»

 

 

 

 

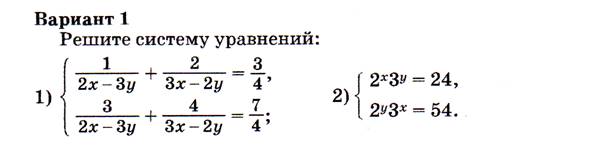
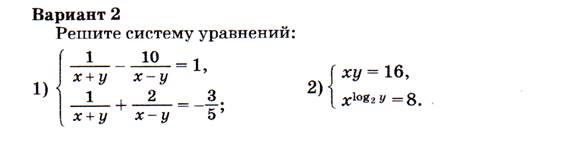
Контрольная работа № 7

по теме «Элементы теории вероятностей и статистики»

 

Контрольная работа № 8

по теме «Комплексные числа»