Самостоятельная работа по теме Осуществление постановки задачи

Самостоятельная работа №1

Тема: Осуществление постановки задачи, составление математической модели, алгоритма решения, проведение анализа работы

Цель: закрепить навыки применения некоторых этапов решения задач.

Вид отчетности: решение в тетради или на листе формата А4.

Время выполнения: 4 часа.

Теоретические сведения:

Решение задач с помощью ЭВМ в упрощенном виде можно представить с помощью следующих этапов: 1) постановка задачи; 2) составление математической модели; 3) разработка алгоритма; 4) создание программы; 5) анализ полученных результатов.

Последняя стадия подразумевает сравнение полученных в программе данных с экспериментальными и другой информацией об объекте. Если выявлены ошибки, то происходит возврат к первому пункту и проверка всех этапов решения.

Некоторые конструкции блок-схем

1)    Полное ветвление: если условие истина, то выполняется ветка S1, иначе ветка S2 (рисунок 1а);

2)    Неполное ветвление: если условие истина, то выполняется ветка S1, в противном случае управление передаётся дальше (рисунок 1б);

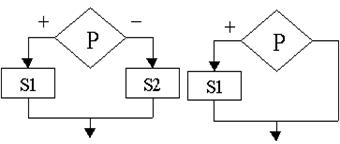
а)                         б)

Рисунок 1 – Полное и неполное ветвление

3)       Циклические конструкции: а) параметрический цикл (рис. 2а): выполняется определённое количество раз; б) цикл с предусловием (рис. 2б): выполняется до тех пор, пока условие – истина; в) цикл с постусловием (рис. 2в): выполняется до тех пор, пока условие – ложь.

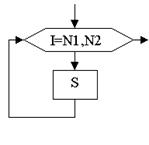
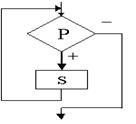
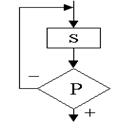
а)                         б)                         в)

Рисунок 2 – Циклические конструкции

Создание математической модели подразумевает выявление исходных данных и результата, математического соотношения между ними.

Ход работы:

1)   осуществить постановку задачи;

2)   составить математическую модель;

3)   изобразить алгоритм решения задачи в виде блок-схемы;

4)   проанализировать решение для конкретных входных данных.

Задания к работе:

1.   По заданному радиусу круга найти его площадь и длину дуги.

2.   Вычислить факториал числа n.

Пояснения к работе:

1.   Обозначим через радиус круга переменную R. Площадь круга находится по формуле: , а длина дуги круга: .

Факториал числа n вычисляется по формуле: n! = 1 ∙ 2 ∙ 3 ∙ … ∙ n. Для решения данной задачи можно использовать любую из циклических конструкций, например, параметрический цикл.

Скачано с www.znanio.ru