Самостоятельная работа на уроках математики как одна из форм развивающего обучения

МКОУ «Лодейнопольская средняя общеобразовательная школа № 68»

Самостоятельная работа

 на уроках математики

как одна из форм развивающего обучения

Прокушева Наталья Геннадьевна

г. Лодейное Поле

2015-2016 уч. год

Знание только тогда знание, когда оно приобретено усилиями своей мысли, а не памятью.

Л.Н.Толстой

Одна из серьезных проблем современной системы образования заключается в том, что традиционно учитель в процессе обучения ориентируется преимущественно на среднего ученика, в то время как ученики с высоким и низким уровнем развития как бы выпадают из «поля зрения» и остаются за «бортом учебного процесса». В связи с этим «сильный» ученик опускается до уровня «среднего», а «слабый» еще больше отстает от сверстников.

Эффективность методики обучения математике напрямую зависит от оптимального решения проблемы формирования и развития самостоятельности учащихся, что соответствует народным традициям Монголии. При воспитании ребенка монголы придерживались определенных правил, соответствующих каждому возрастному периоду по следующем принципам:

– в возрасте до 5 лет возноси как хана;

– в возрасте от 5 до 11 лет – веди за собой словно тень;

– в возрасте от 11 до 16 лет – учи самостоятельности;

– в 16 лет стань для своего ребенка другом.

Анализ психолого-педагогической и методической литературы, анализ педагогического опыта показывают, что эффективным средством формирования познавательной самостоятельности и активности, учащихся в процессе обучения является самостоятельная работа. Проблеме самостоятельной работы посвящены исследования многих педагогов.

Ученик, получая знания и теоретически обоснованные способы действий, может самостоятельно вырабатывать способы решений поставленных проблем. Следует отметить, что в сохранении активности мыслительной деятельности на уроке и дома играет интерес учащегося к тому, что он делает. Одним из инструментов для развития мышления, ведущего к формированию творческой деятельности учащегося, является самостоятельная работа.

При этом самостоятельные работы должны преследовать следующие цели:

– Формирование и дальнейшее развитие мыслительных операций: анализа, сравнения, обобщения и т. д.;

– Развитие и тренинг мышления вообще и творческого в частности;

– Поддерживание интереса к деятельности учащихся вообще;

– Развитие качеств творческой личности, таких, как познавательная активность, упорство в достижения цели, самостоятельность;

– Регулярный контроль успеваемости учащихся по предмету.

Психологи и дидакты выделяют четыре разновидности самостоятельной познавательной деятельности учащихся в процессе обучения. Каждая из них отличается спецификой целеполагания и планирования:

– Постановку цели и планирование предстоящей деятельности ученик осуществляет с помощью учителя;

– Только постановка цели осуществляется с помощью учителя, а планирование предстоящей работы выполняется учеником самостоятельно;

– Постановка цели и планирование предстоящей работы осуществляется учеником самостоятельно в рамках предъявленного учителем задания;

– Работа осуществляется учеником по собственной инициативе; он без помощи учителя, сам определяет содержание, цель, план работы и самостоятельно ее выполняет.

Чтобы преподаватель мог активно вмешиваться в процесс учебного познания и управлять им, необходимо:

▪ разнообразить методы обучения с широким внедрением элементов самостоятельной работы учащихся на уроке;

▪ совершенствовать формы и методы контроля и оценки знаний, умений и навыков учащихся;

▪ осуществлять индивидуальный подход к учащимся.

Познавательная самостоятельность, которая является залогом успешной самостоятельной деятельности, формируется главным образом в процессе их самостоятельной работы. В то же время, в рамках самостоятельной работы наиболее эффективно реализуются идеи уровневой дифференциации, поскольку именно такая форма работы позволяет учащимся работать в своем темпе, выполнять посильные задания, которые учитель подбирает из учета особенностей познавательного и учебного уровня ученика.

И. Унт под самостоятельной работой ученика понимает такой способ учебной работы, где:

▪ учащимся предлагаются учебные задания и руководство для их выполнения,

▪ работа проводится без непосредственного участия учителя, но под его руководством,

▪ выполнение работы требует от учащегося умственного напряжения.

Трудно переоценить значение самостоятельной работы учащихся, потому как без нее невозможен процесс овладения знаниями на различных этапах урока: при изучении нового материала, его закреплении, систематизации, контроле.

Существуют требования к самостоятельной работе:

1) обучать школьников на уроках правильным, рациональным приемам самостоятельной работы;
2) следить, чтобы у учащихся не было перегрузки, вызванной этими заданиями;
3) использовать время на уроках с максимальной продуктивностью.

В теории и практике обучения наиболее распространены следующие подходы к классификации самостоятельных работ:

▪  по дидактическим целям (обучающие, контролирующие, развивающие);

▪ по уровню самостоятельности учащихся (по образцу, реконструктивно-вариативные, частично-поисковые (эвристические), исследовательские (творческие));

▪  по степени индивидуализации (общеклассные, групповые и индивидуальные);

▪ по источнику и методу приобретения знаний (работа с книгой, решение и составление задач, лабораторные и практические работы, подготовка докладов, рефератов и т.д.)

▪  по форме выполнения (устные и письменные самостоятельные работы);

▪  по месту выполнения (классные и домашние).

Рассмотрим некоторые виды самостоятельных работ и их сочетание более подробно.

Классификация по степени индивидуализации включает общеклассные, групповые и индивидуальные самостоятельные работы. Их проводят, в той или иной мере учитывая индивидуальные особенности каждого ученика, в условиях органического соединения индивидуальной и коллективной деятельности учащихся.

Самостоятельные работы по дидактическому назначению можно разделить на обучающие, контролирующие и развивающие.

Обучающие работы предназначены для организации самостоятельной деятельности учащихся, ориентированной на усвоение знаний и выработку умений применять их. Они часто носят индивидуальный характер и предназначены для ребят, по тем или иным причинам, не усвоившим материал вместе с остальной частью класса. Обучающие самостоятельные работы в свою очередь подразделяют на работы по формированию знаний и работы по формированию умений. Во всех случаях надо стремиться проводить обучающие работы в непринужденной, деловой обстановке, чтобы ребята не боялись задавать любые вопросы, были бы уверены, что за ошибки их не накажут, а там, где требуется, помогут, покажут, повторно разъяснят непонятое.

В приложении 1 представлены примеры обучающей (корректирующей) самостоятельной работы по алгебре и началам анализа в 10-м классе. Она предлагается ученикам в виде карточек, в которых присутствуют следующие пункты:

• опорная формула;
• решенные примеры;
• примеры для самостоятельного решения.

Для большей эффективности самостоятельной работы учащихся в процессе обучения я применяю тесты с выбором ответа и карточки-задания. В таких работах я стараюсь включать вопросы, которые устанавливают связь между новым материалом и ранее изученным.

Развивающие самостоятельные работы даются либо индивидуально каждому ученику, либо всему классу сразу с целью привлечения внимания к нестандартным заданиям, которые способствуют развитию логического мышления. Такие задания полезно давать ученикам в качестве домашней работы. На уроках развивающим задачам обычно отводят немного времени и предлагают ученикам в конце урока, если остается время после изучения запланированного материала, либо в начале, в качестве разминки. Если систематически уделять 5-10 минут урока таким задачам результаты не заставят себя ждать.

Например:

1. Найти сходство (общие признаки, свойства, характеристики) у разных геометрических объектов (у ромба и прямоугольника; треугольника и трапеции; окружности и сферы; смежных углов и вертикальных углов и т. д.).

2. а) Перечислить как можно больше геометрических объектов с данным свойством (имеет прямой угол; содержит 4 отрезка; диагонали точкой пересечения делятся пополам; можно вписать окружность). б) Перечислить как можно больше предметов, обладающих несколькими заданными свойствами (имеет прямой угол и острый; имеет два равных угла).

Развивающими являются самостоятельные работы с переадресацией цели. Например, задания с кодами. На урок задаются примеры, решая которые ученик получает ответ. Все ответы и посторонние значения заносятся в таблицу, где напротив значения указана буква или слог. Из полученных ответов-букв (слогов) складываются слова или предложения.

Контролирующие самостоятельные работы призваны проверить степень усвоения материала учениками для своевременной коррекции знаний и накопления оценок. Нередко со всеми учащимися класса проводятся двух и более вариантные самостоятельные работы, идентичные по содержанию. Ныне же все большее применение получают дифференцированные самостоятельные работы, соответствующие разному уровню подготовленности учащихся одного и того же класса. Обычно в практике обучения используются до восьми вариантов разноуровневых заданий.

Математический диктант – давно оправдавшая себя форма самостоятельной работы. Он может носить как контролирующий, так и обучающий характер. Математический диктант предусматривает несколько заданий. Текст вопросов, легко воспринимаемый на слух, требует краткого ответа и несложных вычислений. Для проведения диктанта можно использовать звукозаписи, что позволяет проводить двух вариантные диктанты (например, мужской голос читает I в., женский II в) это дает время на выполнения задания учащимся одного варианта, пока другой вариант слушает свое задание.

Экспресс-диктант проводится как обычный диктант, но ответы записываются учащимися в двух экземплярах (под копирку). Контрольный экземпляр сдается преподавателю, по оставшемуся экземпляру идет фронтальная проверка. Достоинством такой работы является быстрая обратная связь.

Опрос-эстафета. Проводится как соревнование трех команд. По указанию учителя учащиеся выходят по одному из команды, выполняют часть примера своего варианта и передают “эстафету” следующему по команде.

При оценке учитывается не только скорость выполнения задания, но и качество решения. Такие работы вызывают интерес и активизируют работу учащихся. Для активизации работы учащихся с успехом применяю работы – пяти минутки, проводимые в начале урока, для установления рабочего настроя учащихся или в конце урока для подведения итогов занятия. Такие самостоятельные работы значительно повышают внимание учащихся на уроке.

В своей практике для развития самостоятельности мышления, я использую самостоятельные и контрольные работы не менее чем в четырех вариантах. В зависимости от степени сложности темы, работы дифференцируются по уровням сложности. Обычно применяю 2 уровня сложности, реже три. К первому, более легкому уровню, часто прилагается справочный материал, опорные формулы.

Например:

1. Двухуровневая многовариантная самостоятельная работа по алгебре в 9 классе по теме «Арифметическая прогрессия. Формула n-го члена арифметической прогрессии». Самостоятельная работа составлена в двух уровнях сложности. Варианты, помеченные индексами «В – I – 1» – «В – I – 4» предназначены для учеников со слабой математической подготовкой. В них приводятся формулы необходимые для успешного решения первых двух заданий. Варианты «В – II – 1» – «В – II – 6» предназначены для учеников с хорошей и отличной подготовкой. В таких карточках формулы не приводятся, но учитель разрешает использовать справочный материал (шпаргалки), заранее изготовленные дома. (Вообще, я поощряю желание детей использовать и готовить справочный материал с формулами, поскольку в процессе его изготовления и использования, формулы запоминаются сами собой). (См. Приложение 2).

2. Контрольная работа по алгебре в 9 классе № 5 по теме: «Геометрическая прогрессия». В 4-х однотипных вариантах.  (См. Приложение 3).

Одним из видов самостоятельных ра6от, являются работы в которых дифференцирована лишь помощь, оказываемая учащимся. Основу такой работы составляют одни и те же задания. Варьируется только система указаний для групп учащихся с различным уровнем подготовленности. Такие работы Г.И. Саранцев называет многовариативными. Степень подсказок может быть разной, вплоть до заполнения пропусков необходимыми вычислениями. (См. Приложение 4).

Рассмотрим структурно-логические связи самостоятельных работ, классифицируемых по уровню самостоятельности:

Самостоятельная работа по образцу, заготовленному на доске или на карточке. Учащиеся выполняют аналогичное задание с измененными данными цель работы: закрепление изученного материала, например, формул, решение типовых задач.

При выполнении самостоятельных работ по образцу учащиеся не выходят за рамки воспроизводящей деятельности, которая направлена на овладение основными знаниями, умениями, способами работы. Предлагаемые при этом задания выполняются по образцам и алгоритмам, показанным учителем или подробно описанным в учебнике. Они играют важную роль при первичном закреплении изученного, ибо способствуют созданию условий для перехода учащихся к выполнению заданий, требующих более высокого уровня самостоятельности. Поэтому учитель должен уметь отбирать, вовремя предъявлять и требовать от учащихся их точного воспроизведения. (См  Приложение 5)

В приложении 6 приводится самостоятельная работа по алгебре для 8 класса по теме «Числовые промежутки». Она носит контролирующий характер, но в ней приведены примеры решения каждого из заданий.

Самостоятельные работы реконструктивно-вариативного вида обычно содержат в себе задачи, по условиям которых учащимся приходится анализировать новые для них ситуации, переформулировать их, выбирать из известных способов наиболее рациональные. Они отличаются от работ по образцу тем, что при их выполнении необходимо преобразовать исходные данные, т.е. проявить более высокий уровень самостоятельности.

Обычно состоит из 3–4 последовательных заданий, где решение каждого последующего опирается на результат предыдущего. Учащиеся, решив первый пример, сверяют результат с ответами ко всем примерам. Если ответ не совпадает ни с одним, то учащийся возвращается к решению, исправляет ошибку и только тогда приступает к решению второго примера.

Такие работы развивают внимательность и самоконтроль.

Еще более высокий уровень самостоятельности учащиеся проявляют при выполнении частично-поисковых (эвристических) работ, требующих переноса знаний и умений в необычные, нестандартные ситуации. Обычно эвристические задачи используются при проведении олимпиад, турниров, конкурсов.

Высшая степень самостоятельности учащихся проявляется при выполнении исследовательских (творческих) самостоятельных работ. Здесь, пользуясь накопленными знаниями и умениями, выдвигая и проверяя собственные гипотезы и суждения, они учатся открывать для себя новые сведения об изучаемых объектах. Такие задачи обладают наибольшим развивающим потенциалом. Полезно сначала задавать подобные самостоятельные работы на дом, чтобы ребенок мог попробовать решить задачу без помощи учителя, вникнуть в суть, предложить свой способ решения, а уже затем обсудить решение всем коллективом. Включают возможность решения задач несколькими способами, составление задач и примеров самими учащимися и т.п. наиболее важны из всех видов самостоятельных работ.

Учащихся следует обучать умениям и навыкам самостоятельного учебного труда, среди которых одним из основных является умение работать с учебной, справочной и периодической литературой. Для обучения учащихся внимательному и целенаправленному чтению на уроке я вначале излагаю новый материал, а затем предлагаю учащимся самостоятельно прочитать соответствующий параграф, обращая особое внимание на основные положения.

После изучения определенного раздела, темы учащимся предлагается подготовить сообщения, доклады, рефераты для выступления на уроке, на занятиях кружка. Темы выбираются заранее. К этой работе привлекают всех учащихся с учетом их индивидуальных особенностей и способностей.

Написание докладов и рефератов – высшая ступень самостоятельной работы с книгой, так как она связана с чтением нескольких литературных источников, использование первоисточников, выборкой и систематизацией материала. В процессе подготовки учащиеся используют учебник, научно-популярную литературу, журналы. Я стараюсь оказывать им постоянную помощь в подборе литературы, составлении плана, тезисов и т.д.

Одной из форм обучения математике, способствующих развитию и воспитанию графических и вычислительных навыков и умений, является лабораторно-графическая работа.

Характерными особенностями лабораторно-графических работ являются:

а) построение графиков и их применение;

б) использование чертежных, измерительных и вычислительных инструментов;

в) вычислительная обработка результатов измерений с помощью необходимых формул и сравнение результатов измерений и вычислений;

г) применение таблиц, справочной литературы, включая учебники и специальные описания или инструкции.

Лабораторно-графические работы имеют большое воспитательное и образовательное значение. Они позволяют полнее и сознательнее уяснить математические зависимости между величинами, познакомиться с измерительными и вычислительными инструментами и их применением на практике, научиться измерять и вычислять с определенной степенью точности. Индивидуальная самостоятельная работа учащихся вырабатывает умение правильно, аккуратно и четко выполнять чертежи, проводить вычисления. Лабораторно-практические работы дают возможность совершенствовать навыки приближенных вычислений, практику работы с математическими таблицами, а также устанавливать более тесные связи между различными школьными предметами.

При проведении лабораторно-графических работ графический метод применяется не только в вычислительной работе, но и при исследовании функций, решении уравнений, неравенств, систем уравнений и неравенств. (См. Приложение 7).

Лабораторно-графические работы вносят разнообразие в уроки математики, повышают активность и самостоятельность учащихся на уроке, дают возможность обеспечить повышение качества знаний учащихся по математике. При правильной организации лабораторно-графических работ воспитываются культура труда (умение организовать рабочее место, содержать его и инструменты в порядке), привычка к систематическому труду, уважение к работе, стремление к познанию и постоянному совершенствованию полученных знаний и навыков, вырабатывается сознательная дисциплина, чувство ответственности и эстетический вкус искусства. Изящно выполненная работа способствует развитию чувства красоты, удовлетворенности от проделанной работы.

Самостоятельные работы разных типов и видов с большим или малым количеством вариантов призваны обеспечить индивидуализацию обучения, его гуманизацию. Они направлены в первую очередь на развитие познавательной самостоятельности ребенка, которая очень необходима для жизни в современном информационном обществе.

Как же научить учащихся работать самостоятельно на уроке? Необходимо регулярно во время совместной работы учителя со всеми учащимися обучать их приемам самостоятельной работы: самоконтролю и самооценке. Необходимо отрабатывать организационные формы коллективной (парной) самостоятельной работы, включая эти формы в процесс объяснения или закрепления. Чтобы самостоятельная учебная деятельность протекала успешно, необходимо обязательно проверить у каждого результаты всех видов самостоятельной работы. Такую контролируемость можно осуществить, доверив большую часть учащимся.

Каждый учащийся может оценить свой уровень самостоятельности при решении любых задач. (См. Приложение 8).

Опыт моей работы позволяет сделать следующие выводы:

1.      Одним из путей развития творческой активности учащихся, совершенствования процесса обучения математике является умело организованная система самостоятельных работ.

2.      Систематическое проведение самостоятельных работ и повышение их учебно-познавательной роли в учебном процессе содействует значительному улучшению качества математической подготовки школьников.

3.      Органически связывая изучение теоретических вопросов с практической деятельностью, самостоятельные работы дают возможность самостоятельно ликвидировать пробелы в знаниях, расширять знания, творчески применять их в решении различных практических задач.

4.      Контроль за выполнением самостоятельных работ содействует организации тематического учёта знаний школьников, помогает мобилизовать деятельность учащихся, способствует развитию мышления учащихся.

Приложение 1

Обучающая самостоятельная работа (с/р по образцу) по теме
«Правила вычисления производной»

В - 1

2.                                                        

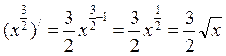
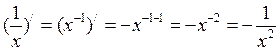
3.      Решите самостоятельно: 
 а)          б)             в)               г)

____________________________________________________________________________

В - 2

2.                                                        

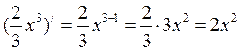
3.      Решите самостоятельно: 
 а)              б)                в)

____________________________________________________________________________

В - 3

2.                                    

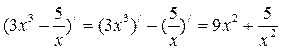
3.      Решите самостоятельно: 
 а)              б)                  в)

____________________________________________________________________________

В - 4

2.                                    

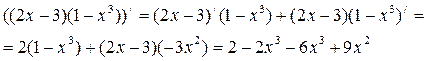
3.      Решите самостоятельно: 
 а)                 б)                     в)

В - 5

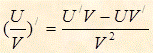
2.                                    

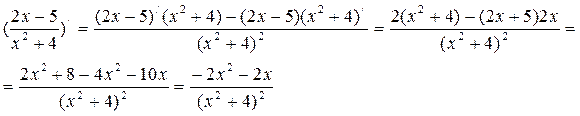
3.      Решите самостоятельно: 
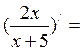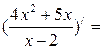 а)                 б)                     в)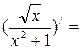

Обучающая самостоятельная работа (с/р по образцу) по теме
«Уравнение касательной»

В – 1. Угловой коэффициент касательной.

1. Угловой коэффициент касательной, проведённой к графику функции   y = f(x)  в точке x₀, находится по формуле:  k = f '(x), причём  k = tgα, где α – угол наклона касательной к оси абсцисс.
2. Вычислить угловой коэффициент касательной, проведённой к графику функции f  в точке А:

а)  f(x) = 3x² + 1,  A(1; 4).         Решение:   f ‘(x) = 6x,  k =f ‘(1) = 6.                                Ответ:   6.

б) f(x) = –3cos x,  A().       Решение:   f '(x) = –3sin x,  k =f ‘() = –3 sin= –3.    Ответ: –3.

3. Решите самостоятельно:   Вычислить угловой коэффициент касательной, проведённой к графику функции f  в точке А:

а)  f(x) =sin 3x,  A();         б) f(x) = 3x³ – x,  A(1; 2).      

___________________________________________________________________________

В – 2. Уравнение касательной к графику функции y = f(x).

1.      y = f(x₀)+f '(x₀)(x – x₀)

для нахождения уравнения касательной к графику функции y = f(x)  в точке с абсциссой  x₀ выполни следующие действия:

1)      Найди  f ‘(x).

2)      Вычисли  f ‘(x₀) и  f (x).

3) Подставь полученные данные в формулу  y = f(x₀)+f '(x₀)(x – x₀)

2.       Решите самостоятельно:    Напиши уравнение касательной к графику функции  y = f(x)  в точке с абсциссой  x₀,  заполнив таблицу.

Приложение 2

Обучающая самостоятельная работа по теме
«Арифметическая прогрессия»

В – I – 1

1.       В арифметической прогрессии (а_n) известны  а₁ = – 0,8, d = – 0,4. Найдите а₂, а₃, а₇ .

ИСПОЛЬЗУЙ ФОРМУЛЫ

а₂ = а₁ +d , а₃ = а₂ +d,

а_n = а₁ +d(n – 1) ?     а₇ = а₁ +d(7 – 1)

2.    Арифметическая прогрессия (а_n) задана последовательностью: 3; 7; … (здесь а₁ = 3 , а₂ = 7). Найдите d , а₃, а₄, а₁₁.

ИСПОЛЬЗУЙ ФОРМУЛЫ

d = а₂ – а₁, а₃ = а₂ +d, а₄ = а₃ +d

а_n = а₁ +d(n – 1) ? а₁₁ = а₁ +d(11 – 1)

3.      Найдите первый член а₁ арифметической прогрессии (а_n), если а₈ = 19, d = 1,2

В – I – 2

1.    В арифметической прогрессии (а_n) известны   а₁ = – 6, d = – 0,5. Найдите а₂, а₃, а₁₂ .

ИСПОЛЬЗУЙ ФОРМУЛЫ

а₂ = а₁ +d , а₃ = а₂ +d,

а_n = а₁ +d(n – 1) ? а₁₂ = а₁ +d(12 – 1)

2.       Арифметическая прогрессия (а_n) задана последовательностью: 2; 3,5; …   (здесь а₁ =2, а₂ = 3,5).

Найдите d , а₃, а₄, а₁₁.

ИСПОЛЬЗУЙ ФОРМУЛЫ

d = а₂ – а₁, а₃ = а₂ +d, а₄ = а₃ +d

а_n = а₁ +d(n – 1) ? а₁₁ = а₁ +d(11 – 1)

 3.   Найдите первый член а₁ арифметической прогрессии (а_n), если а₁₁ = –5, d = –0,7

В – I – 3

1.       В арифметической прогрессии (а_n) известны   а₁ = – 12,5, d = 1,5. Найдите а₂, а₃, а₁₀ .

ИСПОЛЬЗУЙ ФОРМУЛЫ

а₂ = а₁ +d , а₃ = а₂ +d,

а_n = а₁ +d(n – 1) ? а₁₀ = а₁ +d(10 – 1)

2.    Арифметическая прогрессия (а_n) задана последовательностью: 81; 77; … (здесь а₁ = 81, а₂ = 77). Найдите d , а₃, а₄, а₁₆.

ИСПОЛЬЗУЙ ФОРМУЛЫ

d = а₂ – а₁, а₃ = а₂ +d, а₄ = а₃ +d

а_n = а₁ +d(n – 1) ? а₁₆ = а₁ +d(16 – 1)

3.      Найдите первый член а₁ арифметической прогрессии (а_n), если а₁₆ = –11, d = –1

В – I – 4

1.       В арифметической прогрессии (а_n) известны   а₁ = 5,5, d = 2,5. Найдите а₂, а₃, а₁₁ .

ИСПОЛЬЗУЙ ФОРМУЛЫ

а₂ = а₁ +d , а₃ = а₂ +d,

а_n = а₁ +d(n – 1) ? а₁₁ = а₁ +d(11 – 1)

 2.   Арифметическая прогрессия (а_n) задана последовательностью: 2,6; 2,4; … (здесь а₁ =2,6, а₂ = 2,4).

Найдите d , а₃, а₄, а₂₁.

ИСПОЛЬЗУЙ ФОРМУЛЫ

d = а₂ – а₁, а₃ = а₂ +d, а₄ = а₃ +d

а_n = а₁ +d(n – 1) ? а₂₁ = а₁ +d(21 – 1)

3.    Найдите первый член а₁ арифметической прогрессии (а_n), если а₈ = 37, d = 3.

Контролирующая самостоятельная работа по теме
«Арифметическая прогрессия»

В – II – 1

1.   Арифметическая прогрессия (а_n) задана последовательностью: 2; 9;… Найдите d, а₃, а₄, а₂₁.

2.   Найдите разность d арифметической прогрессии (а_n), если а₁ = 5, а₈ = 19.

3.   Известны два члена арифметической прогрессии (а_n): а₈ = 11,2 и а₁₅=19,6. Найдите а₁ и d.

В – II – 2

1.   Арифметическая прогрессия (а_n) задана последовательностью: 17,6; 17,2;… Найдите d, а₃, а₄, а₂₁.

2.   Найдите разность d арифметической прогрессии (а_n), если а₁ = 2, а₈ = -5.

3.   Известны два члена арифметической прогрессии (а_n): а₁₀ =1,9 и а₁₆ =6,1.  Найдите а₁ и d.

В – II – 3

1.   Арифметическая прогрессия (а_n) задана последовательностью: -50; -38,8;… Найдите d, а₃, а₄, а₂₁.

2.   Найдите разность d арифметической прогрессии (а_n), если а₁ = –0,5, а₇ = 1,9.

3.   Известны два члена арифметической прогрессии (а_n): а₅ = 8,2 и а₁₀ =4,7.   Найдите а₁ и d

В – II – 4

1.   Арифметическая прогрессия (а_n) задана последовательностью: -15,3; -14,7;… Найдите d, а₃, а₄, а₂₁.

2.   Найдите разность d арифметической прогрессии (а_n), если а₁ = 16, а₈ = 37.

3.   Известны два члена арифметической прогрессии (а_n): а₄ =32,5 и а₁₂ =29,3.   Найдите а₁ и d.

В – II – 5

1.   Арифметическая прогрессия (а_n) задана последовательностью: 3,4; – 0,2;… Найдите d, а₃, а₄, а₂₁.

2.   Найдите разность d арифметической прогрессии (а_n), если а₁ = 4, а₁₆ = – 11.

3.   Известны два члена арифметической прогрессии (а_n): а₇ =4,9 и а₁₇ =10,9.  Найдите а₁ и d.

В – II – 6

1.   Арифметическая прогрессия (а_n) задана последовательностью: 18; 14;… Найдите d, а₃, а₄, а₂₁.

2.      Найдите разность d арифметической прогрессии (а_n), если а₁ = 17,5, а₁₆ = 40.

3.   Известны два члена арифметической прогрессии (а_n): а₆ =36,4 и а₁₈=31,6.  Найдите а₁ и d.

Ответы:

Приложение 3

Контролирующая самостоятельная работа по теме
«Геометрическая прогрессия»

В – 1

1.  Последовательность (b_n) – геометрическая прогрессия.   Найдите b₂ и b₇ , если b₁ =–24 и знаменатель q =0,5.

2.  Найдите сумму первых шести членов геометрической прогрессии (x_n), первый член которой равен 3, а знаменатель равен 2.

3.  Найдите сумму пяти первых членов геометрической прогрессии (b_n) с положительным знаменателем, зная, что b₃ = 0,05 и  b₅ =0,45.

4. Между числами 6 и 486 вставьте такие три числа, чтобы они вместе с данными образовывали геометрическую прогрессию. Возможны два варианта.

В – 2

1.  Последовательность (b_n) – геометрическая прогрессия.  Найдите b₂ и b₅ , если b₁ = 625 и знаменатель q = –1/5.

2.  Найдите сумму первых шести членов геометрической прогрессии (x_n), первый член которой равен 4, а знаменатель равен 2.

3.  Найдите сумму пяти первых членов геометрической прогрессии (b_n) с положительным знаменателем, зная, что b₃ = 0,04 и b₅ = 0,16.

4. Между числами и 27 вставьте такие три числа, чтобы они вместе с данными образовывали геометрическую прогрессию. Возможны два варианта.

В – 3

1.  Последовательность (b_n) – геометрическая прогрессия. Найдите b₂ и b₆ , если b₁ = 0,81 и знаменатель q = –1/3.

2.  Найдите сумму первых шести членов геометрической прогрессии (x_n), первый член которой равен 5, а знаменатель равен 2.

3.  Найдите сумму пяти первых членов геометрической прогрессии (b_n) с положительным знаменателем, зная, что b₃ = 1,2 и b₅ = 4,8

4. Между числами 15 и 1215 вставьте такие три числа, чтобы они вместе с данными образовывали геометрическую прогрессию. Возможны два варианта.

В – 4

1.  Последовательность (b_n) – геометрическая прогрессия. Найдите b₂ и b₅ , если b₁ = –125 и знаменатель q =1/5.

2.  Найдите сумму первых шести членов геометрической прогрессии (x_n), первый член которой равен 6, а знаменатель равен 2.

3.  Найдите сумму пяти первых членов геометрической прогрессии (b_n) с положительным знаменателем, зная, что b₃ = 3,6 и b₅ = 32,4.

4. Между числами 0,5 и 8 вставьте такие три числа, чтобы они вместе с данными образовывали геометрическую прогрессию. Возможны два варианта.

Приложение 4

Многовариативная самостоятельная работа по теме

«Определение производной»

В – 1

Пользуясь определением производной, найдите значение производной функции  f(x) = x² – 3  в точке  x₀ = –1.

В – 2

Пользуясь определением производной, найдите значение производной функции  f(x) = x² – 3  в точке  x₀ = –1.

Указание.   Используйте алгоритм:

1. Δx,  Δf = f(x₀ + Δx) – f(x₀),  где  x₀ = –1.
2. Найдите  .
3. Определите,  к чему стремится  при  Δx  стремящемся к 0?

В – 3

Пользуясь определением производной, найдите значение производной функции  f(x) = x² – 3  в точке  x₀ = –1.

Указание.   Выполни действия в соответствии с приведёнными ниже указаниями::

4. Пользуясь формулой  Δf = f(x₀ + Δx) – f(x₀),  найди  Δf,  т.е.  Δf = (f(x₀ + Δx)² – 3) – (x₀² – 3) = …  (продолжи).   

Найди  Δf   при  x₀ = –1.

5. Найдите    (Δf  бери в точке  x₀).
6. Определи,  к чему стремится  при  Δx  стремящемся к 0?

Многовариативная самостоятельная работа по теме

«Уравнение касательной»

Составьте уравнение касательной к графику функции f в точке с абсциссой  x₀.  Напишите уравнение одной из прямых параллельных этой касательной.

В – 1

f(x) = x² – 3x – 1,  x₀ = 1.

В – 2

f(x) = 2x² – 5x + 1,  x₀ = 2.

В – 3

f(x) = 3x² – 4x – 2,  x₀ = 1.

В – 4

f(x) = x² – 3x – 4,  x₀ = 1.

В – 5

f(x) = x² – 2x – 13,  x₀ = 12.

Указания:

1. Вспомните, когда две прямые параллельны.
2. Не забудьте, что прямые параллельны, когда равны их угловые коэффициенты.
3. а) Найдите уравнение касательной  y = f(x₀)+f '(x₀)(x – x₀).

б) Две прямые параллельны, когда равны их угловые коэффициенты. То есть, если уравнение касательной  y = kx + b, то уравнение прямой параллельной ей  y = kx + c,  где с – любое число.

Приложение 5

Вариант 1.

Образец:   Найдите число, если его 20% равны 80.

                   Решение:    20% =  = 0,2;      80 : 0,2 = 800 : 2 = 400

1. Найдите число, если 40% его равно 120.
2. Курящие дети сокращают жизнь на 10%, что составляет 7 лет. Определите, какова продолжительность жизни нынешних курящих детей.

Вариант 2.

Образец:   Найдите число, если его 30% равны 90.

                   Решение:    30% =  = 0,3;        90 : 0,3 = 900 : 3 = 300

1.  Найдите число, если 25% его равно 275.

2.      Курящие дети сокращают жизнь на 10%, что составляет 7 лет. Определите, какова продолжительность жизни нынешних курящих детей.

Вариант 3.

Образец:   Найдите число, если  его равны 160.

                   Решение:    160 :  =  = 280

1.  Найдите число, если   его равно 125.

2. Статистика показывает, что в одной из школ Санкт-Петербурга насчитывается курящих подростков , что составляет 650 человек. Определите, сколько курящих детей в этой школе?

Вариант 4.

Образец:   Найдите число, если  0,6  его равны 360.

                   Решение:    360 : 0,6 = 3600 : 6 = 600

1.  Найдите число, если  0,8 его равно 24.

2. Если у новорожденного ребёнка курит отец, то его вес будет меньше среднего на 12%, что составляет 360 г. Чему равен средний вес новорожденного ребёнка, у которого курит мать?

Приложение 6

Приложение 7

РЕШЕНИЕ УРАВНЕНИЯ (НЕРАВЕНСТВА СИСТЕМЫ)

 ГРАФИЧЕСКИМ МЕТОДОМ

1. Определить, можно ли преобразовать каким- нибудь способом уравнение (неравенство) к виду  f(x)=g(x)  (f(x)  <  g(x)).

2. Если п.1 имеет место, выполнить преобразования, выбрав f(x) и g(x) наиболее простого вида.

3. Построить графики функций y=f(x) и y=g(x)  в одной и той же системе координат.

4. Наити абсциссы точек пересечения графиков, каждая из них есть x₀ -корень данного уравнения.

5. Найти промежутки оси абсцисс (связанные с x₀), для которых график функции y=f(x) расположен выше графика функции y=g(x) , каждый из них есть решение данного неравенства.

6. Найти координаты точек  x₀-y₀,  каждая пара есть решение системы уравнений.

7. Записать ответ.

ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ.

В зависимости от того, что известно о функции, построить её график одним из следующих способов:

А. По точкам (на основании определения графика):

1. Задать  таблицу возможно большего количества пар соответствующих значений аргумента и функции, удобных для вычислений (или использовать микрокалькулятор).
2. Построить в выбранной системе координат точки с координатами, соответственно равными значениям аргумента и функции.
3. Соединить полученные точки плавной линией.

Б. По характеристическим точкам (если они существуют и общий вид графика известен, например у прямой или параболы):

1. Найти (вычислить координаты) и построить в выбранной системе координат характеристические точки графика данной функции.
2. Зная общий вид графика, соединить точки известной линией.

В. Путём сдвига и деформации графика известной функции y=f(x), связанной с данной некоторыми соотношениями, по правилам:

1. y=f(x)+b – параллельный перенос графика y=f(x) на вектор r(0;b).
2. y=f(x+a) – параллельный перенос графика y=f(x) на вектор r(-a;0).
3. y=k(x) – умножение ординаты графика y=f(x) на k (при k > 1 – растяжение,

при 0 <  k  <  1 –  сжатие к оси абсцисс).

4. y=-f(x) (частный случай предыдущего при k= -1) – симметрия графика y=f(x) относительно оси абсцисс.
5. y=f(kx) –деление ординаты графика y=f(x) на k (при k > 1 – сжатие, при  0 < k < 1 – растяжение к оси ординат).
6. y=f(-x) (частный случай предыдущего при k= -1) – симметрия графика функции y=f(x) относительно оси ординат.
7. y=|f(x)| –симметрия относительно оси абсцисс тех участков графика функции y=f(x), которые расположены ниже её.
8. y=f(|x|) –симметрия относительно оси ординат графика y=f(x), построенного на положительной полуоси абсцисс.
9. x=f(y) – симметрия относительно биссектрисы первого и третьего координатных углов.

Г. На основе общего исследования свойств функции и её графика с помощью производной  (установление точек экстремума, промежутков монотонности, вогнутости и выпуклости кривой и точек её перегиба).

Приложение 8

Лист оценки уровня самостоятельности учащихся

(отметить в каждом параметре один из показателей)

1.          1)Меня побуждает к самостоятельной деятельности несколько причин;

     2)   Меня побуждает одна постоянная причина;

     3)  Меня побуждает то одна причина, то другая;

     4)  Меня ничто не побуждает к самостоятельной деятельности.
2.  1).Я активен, если требуется исследование, нестандартное решение;

      2) Я предпочитаю не слишком трудные задания, но требующие размышления
           объяснения своими словами;

      3)  Я активно выполняю только несложные задания;

      4)  При выполнении самостоятельной работы я не проявляю активности.
3.  1)   Выполняя самостоятельную работу, я умею организовать свое рабочее
         место, умею планировать время, выстраивать план работы;

    2)  Умею организовать свое рабочее место, умею планировать время;

    3)  Умею организовать рабочее место;

    4)  Не умею организовать свою самостоятельную работу без помощи учителя.
4.   1)  Могу любую работу на уроках и дома выполнять без контроля со стороны
          взрослых; сам себя контролировать;

     2) Чаще в контроле не нуждаюсь;

     3)  Меня заставляет быть ответственным контроль со стороны взрослых;

     4)  К сожалению, заставить себя быть ответственным не могу ни я, ни взрослые.

5.  1)  Могу выполнить без помощи любое задание;

    2)  Без помощи могу выполнить не очень трудное задание;

    3)  Обычные задания выполняю при небольшой помощи учителя;

    4)  При выполнении заданий всегда нуждаюсь в помощи учителя.