

Министерство образования и науки Самарской области
государственное автономное профессиональное образовательное учреждение Самарской области
«ТОЛЬЯТТИНСКИЙ МАШИНОСТРОИТЕЛЬНЫЙ КОЛЛЕДЖ»
сборник методических указаний для ОБУЧАЮЩИХСЯ
по выполнению ПРАКТИЧЕСКИХ работ
НА ПРАКТИЧЕСКИХ ЗАНЯТИЯХ
ЕН.01 ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
программы подготовки специалистов среднего звена
09.02.07 Информационные системы и программирование
Тольятти, 2018
|
Составитель:
Рожнова Г.И. преподаватель ГАПОУ СО «ТМК».
Сборник методических указаний для обучающихся по выполнению практических работ на практических занятиях является частью программы подготовки специалистов среднего звена ГАПОУ СО «ТМК» по специальности 09.02.07 Информационные системы и программирование в соответствии с требованиями ФГОС СПО.
Сборник методических указаний по выполнению практических работ адресован обучающимся очной формы обучения при изучении дисциплины ЕН.01 Элементы высшей математики.
Настоящий сборник методических указаний включает в себя пояснительную записку, рекомендации по оформлению отчётов по выполняемым практическим работам, непосредственно методические указания по выполнению каждой работы в соответствии с рабочей программой дисциплины ЕН.01 Элементы высшей математики.
|
Содержание |
|
|
Пояснительная записка |
4 |
|
Введение |
5 |
|
Практическая работа №1 Решение задач с комплексными числами |
6 |
|
Практическая работа №2 Вычисление пределов с помощью замечательных пределов, раскрытие неопределённостей |
10 |
|
Практическая работа №3 Полное исследование функций. Построение графиков |
14 |
|
Практическая работа №4 Вычисление площадей плоских фигур и объемов тел вращения с помощью определённого интеграла |
20 |
|
Практическая работа №5 Вычисление частных производных и дифференциалов функций нескольких переменных |
25 |
|
Практическая работа №6 Вычисление двойных интегралов |
29 |
|
Практическая работа №7 Определение сходимости числовых рядов |
37 |
|
Практическая работа №8 Решение дифференциальных уравнений |
42 |
|
Практическая работа №9 Нахождение обратной матрицы |
54 |
|
Практическая работа №10 Решение системы линейных уравнений по формулам Крамера, методом Гаусса и с помощью обратной матрицы |
58 |
|
Практическая работа №11 Решение задач по аналитической геометрии
|
63 |
1. Пояснительная записка
Методические указания к выполнению практических занятий по дисциплине ЕН.01 Элементы высшей математики предназначены для закрепления теоретических знаний, полученных на лекциях, а также для овладения обучающимися умений и навыков применять эти знания при самостоятельной работе.
Перечень практических занятий соответствует рабочей программе по дисциплине ЕН.01 Элементы высшей математики.
Методические указания выполняют функцию управления самостоятельной работой обучающегося, поэтому каждое занятие имеет унифицированную структуру, включающую определение целей занятия, оборудования занятия, порядок выполнения работы, а также задания и контрольные вопросы для закрепления темы.
В результате освоения учебной дисциплины обучающийся должен уметь:
|
Код |
Наименование образовательного результата |
|
У1 |
Выполнять операции над матрицами и решать системы линейных уравнений |
|
У2 |
Решать задачи, используя уравнения прямых и кривых второго порядка на плоскости |
|
У3 |
Применять методы дифференциального и интегрального исчисления |
|
У4 |
Решать дифференциальные уравнения |
|
У5 |
Пользоваться понятиями теории комплексных чисел |
В результате освоения учебной дисциплины обучающийся должен знать:
|
Код |
Наименование образовательного результата |
|
З1 |
Основы математического анализа, линейной алгебры и аналитической геометрии |
|
З2 |
Основы дифференциального и интегрального исчисления |
|
З3 |
Основы теории комплексных чисел |
2. Введение
Уважаемый обучающийся!
Методические указания по дисциплине ЕН.01 Элементы высшей математики для выполнения практических работ созданы Вам в помощь для работы на занятиях, подготовки к практическим работам, правильного составления отчетов.
Приступая, к выполнению практической работы Вы должны внимательно прочитать тему и цель занятия, пояснениями к работе (учебный материал), ответить на вопросы для закрепления теоретического материала.
Все задания к практической работе Вы должны выполнять в соответствии с инструкцией, анализировать полученные в ходе занятия результаты по приведенной методике.
Отчет о практической работе Вы должны выполнить по приведенному алгоритму, опираясь на образец.
Наличие положительной оценки по практическим работам необходимо для получения зачета по дисциплине, поэтому в случае отсутствия на уроке по любой причине или получения неудовлетворительной оценки за практическую работу Вы должны найти время для ее выполнения или пересдачи.
Внимание! Если в процессе подготовки к практическим работам или при решении задач у Вас возникают вопросы, разрешить которые самостоятельно не удается, необходимо обратиться к преподавателю для получения разъяснений или указаний в дни проведения дополнительных занятий.
Время проведения дополнительных занятий можно узнать у преподавателя или посмотреть на двери его кабинета.
Ответ оценивается отметкой «5», если:
- работа выполнена полностью;
- в логических рассуждениях и обосновании решения нет пробелов и ошибок;
- в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
- работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
- допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
- допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
- допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Преподаватель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
3. Сборник практических работ
Тема практической работы № 1:
Решение задач с комплексными числами
Цель работы:
применить умения графического изображения комплексных чисел, выполнения арифметических операций с комплексными числами, заданных в различных формах.
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
|
Вариант 1 |
Вариант 2 |
|
1. Изобразите на плоскости заданные комплексные числа: |
|
|
Z1 = 4i Z2 = 3 + i Z3= - 4 +3i Z4= - 2 -5i |
Z1= -5i Z2= 4 + i Z3= -7 + 2i Z4= -3 – 6i |
|
2 . Вычислите модуль комплексного числа |
|
|
Z = 3 + 4i |
Z = 8 + 6i
|
|
3. Произведите сложение и вычитание комплексных чисел: |
|
|
Z1 = (3 + 5i) , Z2 = (7 – 2i) |
Z1 = (3 – 2i), Z2 = (5 + 3i) |
|
4. Выполните действие над комплексными числами: |
|
|
а)
(2 + 3i)(5 – 7i), в) (3 + 5i)2, г)
|
а)
(3 + 2i)(1 + 3i), в) (2 – 7i)2, г)
|
|
5. Решите уравнения: |
|
|
x2 – 4x + 13 = 0. |
2,5x2 + x + 1 = 0.
|
6. Представить данные комплексные числа в тригонометрической и показательной форме.
7. Вычислить в тригонометрической и показательной формах:
1) z1∙z2; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
|
Z1= 2- 2i; Z2= |
Z1= |
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Комплексные числа - числа вида Z
= a + ib, где a,b – вещественные числа, а i = ![]() - мнимая единица (i2 =
−1). Множество комплексных чисел обозначается C.
- мнимая единица (i2 =
−1). Множество комплексных чисел обозначается C.
Действительные числа a и b комплексного числа Z = a + ib, называются действительной и мнимой частью числа z и обозначаются, соответственно, Rez=x и Imz=y.
Два комплексных числа z1=a + ib и z2=c + id называются равными в том и только том случае, если a = c, b = d.
Запись Z=a + ib называют алгебраической формой комплексного числа z.
 Числа Z=a
+ ib и
Числа Z=a
+ ib и ![]() =a − ib называют комплексно
сопряженными.
=a − ib называют комплексно
сопряженными.
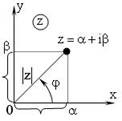
Геометрическое представление комплексного числа
Если рассмотреть плоскость с прямоугольной системой координат, то любому комплексному числу z = a + ib можно сопоставить точку на этой плоскости с соответствующими координатами (a;b), и радиус-вектор R комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу (рис. 1). Данная плоскость называется комплексной. Действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.
![]() - модуль комплексного числа - расстояние
от начала координат до соответствующей точки комплексной плоскости. Попросту
говоря, модуль – это длина радиус-вектора.
- модуль комплексного числа - расстояние
от начала координат до соответствующей точки комплексной плоскости. Попросту
говоря, модуль – это длина радиус-вектора.
![]() , где
, где ![]() - аргумент комплексного числа.
- аргумент комплексного числа.
Действия над комплексными числами в алгебраической форме.
Сложение: Z1 + Z2 = (a+ib)+(c+id) = (a+c) + (b+d)i.
Вычитание: Z1 - Z2 = (a+ib)-(c+id) = (a-c) + (b-d)i.
Умножение: Z1 · Z2 = (a+ib)(c+id)=(ac − bd)+(ad + cb)i.
Деление: ![]() .
.
Умножение на сопряженное: Z · ![]() =(a + bi)(a -bi)= a2 –b2i2=
a2 – b2·(-1) = a2 + b2 –
квадрат суммы
=(a + bi)(a -bi)= a2 –b2i2=
a2 – b2·(-1) = a2 + b2 –
квадрат суммы
Для всякого комплексного числа z = a + ib справедливо равенство:
z=R(cosφ+ isinφ) называют тригонометрической формой комплексного числа,
z = ![]() – называют показательной
формой комплексного числа
– называют показательной
формой комплексного числа
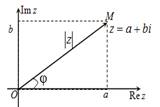 Здесь
Здесь ![]() - модуль комплексного числа - расстояние
от начала координат до соответствующей точки комплексной плоскости. Попросту
говоря, модуль – это длина радиус-вектора.
- модуль комплексного числа - расстояние
от начала координат до соответствующей точки комплексной плоскости. Попросту
говоря, модуль – это длина радиус-вектора.
Угол φ между
положительной полуосью действительной оси и радиус-вектором, проведенным из
начала координат к соответствующей точке, называется аргументом комплексного
числа - ![]() .
.
Действия над комплексными числами в тригонометрической форме.
|
В тригонометрической форме z1 =R1(cosφ1 + isinφ1), z2 =R2(cosφ2 + isinφ2) |
В показательной форме Z1
= |
|
|
Умножение |
Z1 ∙ Z2 = R1∙R2(cos(φ1+φ2) + isin(φ1+φ2)). |
Z1·Z2=
|
|
Деление |
|
|
|
Возведение в степень |
zn =Rn(cos nφ + isin nφ) - формула Муавра |
|
|
Извлечение корня |
|
k = 0,1,2.....n-1 |
При выполнении практической работы рассмотрите следующие примеры:
Пример 1.
Выполнить действия над комплексными числами, представив результат в алгебраической форме:
Z1 = 4+ 5i, Z2 = 6−9i.
Решение: 1) Z1 + Z2 = (4+ 5i) + (6−9i)= 4+6+5i -9i.= 10 – 4i
2) Z1 - Z2 = (4+ 5i) - (6−9i)= 4-6+5i +9i.= -2 + 14i
3) Z1 ·Z2 = (4+5i)(6− 9i)= 24 −36i + 30i− 45i2= 24 -6i - 45·(-1) = 69 -6i.
4) ![]()
Ответ: Z1 +
Z2 =10 – 4i, Z1 - Z2 = -2 + 14i,
Z1 ·Z2 =69 -6i, ![]()
Пример 2.
Раскрыть скобки, используя формулы сокращенного умножения:
1) (2+ 3i)2 = 22 + 2·2·3i + (3i)2 = 4 +12i + 9·(-1) = -5+12i,
2) (5 + 4i)(5 - 4i)= 52 –42i2= 25 – 16·(-1) = 25 + 16 =4,
3) (3-5i)2 = 32 - 2·3·5i + (-5i)2 = 9 - 30i + 25(-1) = -16- 30i.
 Пример 3.
Пример 3.
Изобразим на комплексной плоскости числа
Z1 = 2 + i; Z2 = 3i;
Z3 = -3 + 2i; Z4 = -1 – i.
Пример 4.
А) Представить числа z1
= ![]() ,
, ![]() в тригонометрической и
показательной форме,
в тригонометрической и
показательной форме,
Б) вычислить в
тригонометрической форме: 1) z1∙z2; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
Решение:
А). Получим тригонометрическую и показательную форму z1
= ![]() ,
,
1) Найдем модуль числа - ![]() , 2) Найдем аргумент числа -
, 2) Найдем аргумент числа - ![]() ,
,
3) запишем к.ч. в тригонометрической и показательной форме:
z1 = ![]() .
.
![]() ,
,
1) ![]() - модуль числа,
- модуль числа,
2) ![]() - аргумент числа
- аргумент числа
3) запишем к.ч. в тригонометрической и показательной форме:
![]() .
.
Б) Произведение:
z1∙z2 = ![]()
![]() .
.
Частное:
![]() =
=
![]() .
.
Возведение в степень:
![]()
![]() .
.
Извлечение из под знака корня:
![]() .
.
Пр k=0: ![]() ;
;
Пр k=1: ![]() .
.
Вопросы для закрепления теоретического материала к практическому занятию:
1. Дайте определение комплексного числа.
2. Какие числа называются комплексно – сопряженными?
3. Какие комплексные числа называются равными?
4. Как вычислить модуль комплексного числа?
5. Как производятся действия над комплексными числами в алгебраической форме?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Тема практической работы № 2:
Вычисление пределов с помощью замечательных пределов, раскрытие неопределённостей
Цель работы:
применить умения по вычислению пределов и раскрытию неопределенностей, используя принцип замены эквивалентными, I и II замечательные пределы.
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
I Вариант II Вариант
Вычислить пределы.
1) ![]() 1)
1)
![]()
2) ![]() 2)
2)
![]()
3) 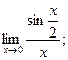 3)
3) ![]()
4) ![]() 4)
4)
![]()
5) ![]() 5)
5)
![]()
6) ![]() 6)
6)
![]()
7) ![]() 7)
7)
![]()
8) ![]() 8)
8)
![]()
9) ![]() 9)
9) ![]()
10) ![]() 10)
10)![]()
![]()
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
![]() - 1-й замечательный предел.
- 1-й замечательный предел.
Следствие.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() – 2-й замечательный предел.
– 2-й замечательный предел.
Следствие 1.
![]()
Следствие 2.
Сделаем
замену: ![]() = y
=> x =
= y
=> x = ![]() . Тогда при x→∞,
y→0.
. Тогда при x→∞,
y→0.
Две
бесконечно малые величины 𝛂(x) называются эквивалентными (или равносильными) при x→a, если ![]()
Таблица эквивалентных величин (всюду x→0)
sin![]() x
x
arcsin x![]() x
x
tg x![]() x
x
arctg x![]() x
x
ex-1![]() x
x
ln(1+x)![]() x
x
ax![]() x ln a ,
a≠1, a>0
x ln a ,
a≠1, a>0
loga(1+x)![]()
(1+x)𝛂 -1![]() 𝛂x, 𝛂
𝛂x, 𝛂![]() R
R
1-cos x![]()
При выполнении практической работы рассмотрите следующие примеры:
Пример 1.
![]()
Пример 2.
![]()
![]()
![]()
Пример 3.
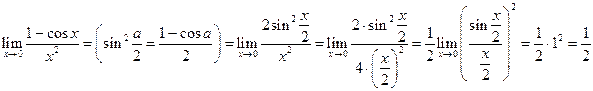
Пример 4.
![]()
Пример 5.
![]()
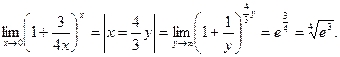
Пример 6.
![]()
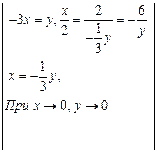 =
=![]()
Пример 7.
![]()
=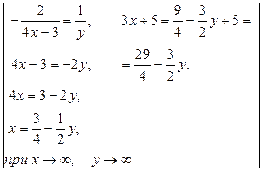 =
=
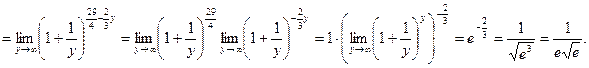
Пример 8.
![]()
Пример 9.
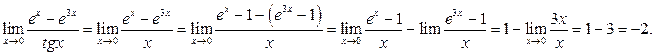
Вопросы для закрепления теоретического материала к практическому занятию:
1. Какие неопределённости вы знаете?
2. Назовите 1-й замечательный предел.
3. Назовите второй замечательный предел.
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Тема практической работы № 3:
Полное исследование функций. Построение графиков.
Цель работы:
применить умения дифференциального исчисления по исследованию функции по схеме и построению график функции на его основе.
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
|
I вариант |
II вариант |
Исследовать и построить графики следующих функций.
а) у![]() х3+х2-5х+3; а)
у
х3+х2-5х+3; а)
у![]() х3+6х2+9х+4;
х3+6х2+9х+4;
б) у =![]() . б)
у =
. б)
у =![]()
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Общая схема построения графиков функций.
График функции.
При выполнении практической работы рассмотрите следующие примеры:
Пример 1.
Исследовать функцию у=х3-5х2+3х-5 построить график.
Функция не является ни чётной ни нечётной.
3. точка пересечения с осью у:
x=0,у=03-5![]() 02+3
02+3![]() 0-5=-5
0-5=-5
(0;-5) – точка пересечения с осью у.
Точки пересечения с осью х найти затруднительно.
4. вертикальных асимптот нет, т.к. функция непрерывна на (-∞;∞).
Наклонная асимптота: у=kх+b.
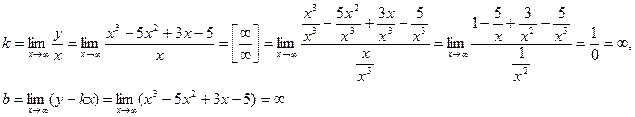 Наклонных асимптот нет.
Наклонных асимптот нет.
5. у/=(х3-5х2+3х-5)/=3х2-10х+3;
у/=0; 3х2-10х+3=0,
D=100-4![]() 3
3![]() 3=100-36=64,
3=100-36=64,
x1=![]()
x2= ![]() .
.
x1=3;х2 = ![]() -критические точки функции.
-критические точки функции.
|
x |
(- |
|
|
3 |
|
|
у/ |
+ |
0 |
- |
0 |
+ |
|
у |
|
|
|
-14 |
|
|
|
|
max |
|
min |
|
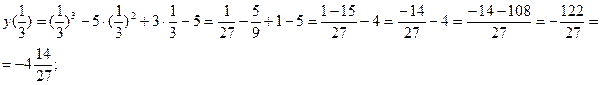
y(3)=33-5![]() 32+3
32+3![]() 3-5=27- 45+9-5= -14
3-5=27- 45+9-5= -14
(![]() ) – точка max; (3;-14) – точка min
) – точка max; (3;-14) – точка min
у//=0 ; 6х-10=0,
6х=10,
x=![]() ,
,
x= ![]() ,
,
x= 1![]() .
.
|
х |
|
|
|
|
у// |
- |
0 |
|
|
у |
|
|
|
|
|
|
точка перегиба |
|
у(![]()
![]() точка перегиба
точка перегиба
|
x |
y |
|
-1 |
-14 |
|
2 |
-11 |
|
4 |
-9 |
|
5 |
10 |
y x
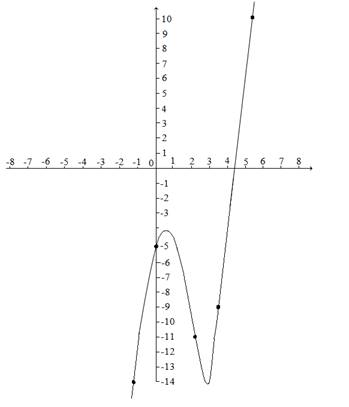
Пример 2.
Исследовать
функцию F(x)=![]() и построить её график.
и построить её график.
1) х-2≠0,
х≠2,
D(f)=(-∞;2)![]() (2;∞)
(2;∞)
2)f(-х)=![]() функция не является ни чётной, ни
нечетной.
функция не является ни чётной, ни
нечетной.
Функция не периодическая.
3) точка пересечения с осью Оу:
x=0; у=0
(0;0) – точка пересечения с осью Оу. Точки пересечения с осью Ох.
y=0, 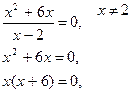
x=0 или х+6=0,
x=-6.
(0;0), (0;-6) – точки пересечения с осью Ох.
4) х=2 – точка разрыва II рода.
![]()
x=2 – вертикальная асимптота.
y= kx+b – наклонная асимптота.
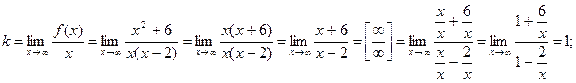
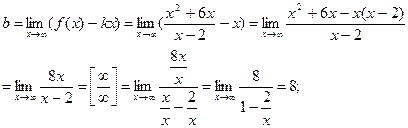
y=1![]() х+8;
х+8;
y= х+8 - наклонная асимптота.
5) ![]()
![]()
у/=0 ![]() , х≠2
, х≠2
х2-4х-12=0
D=16-4![]() 1
1![]() (-12)=16+48=64
(-12)=16+48=64
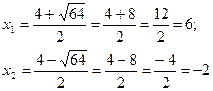
x1=6; х2=-2 – критические точки
|
х |
(-∞;-2) |
-2 |
(-2;2) |
2 |
(2;6) |
6 |
(6; ∞) |
|
у/ |
+ |
0 |
- |
|
- |
0 |
+ |
|
у |
|
2 |
|
|
|
18 |
|
|
|
|
max |
|
точка разрыва |
|
min |
|
y(-2)=![]()
y(6)=![]()
(-2;2) – точка max
(6;18) – точка min
6) у//=![]()
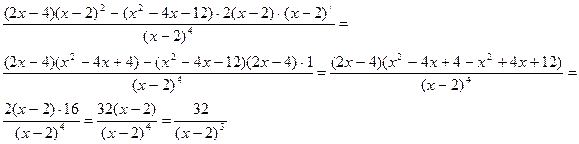
у//=0 ; ![]() х≠2.
х≠2.
32≠0
нет критических точек II рода.
|
х |
(-∞;2) |
2 |
(2; ∞) |
|
у// |
- |
|
|
|
у |
|
|
|
|
|
|
точка разрыва |
|
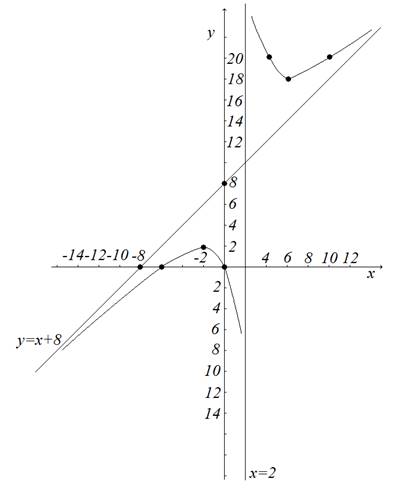 7) дополнительные
точки
7) дополнительные
точки
![]() х у
х у
4 20
10 20
Вопросы для закрепления теоретического материала к практическому занятию:
1. Какая функция называется чётной?
2. Какая функция называется нечётной?
3. Как найти критические точки функции?
4. Общий вид уравнения наклонной асимптоты.
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Тема практической работы № 4:
Вычисление площадей плоских фигур и объемов тел вращения с помощью определённого интеграла
Цель работы:
применить умения по нахождению геометрического смысла интеграла для вычисления площадей плоских фигур и объемов тел вращения
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
I Вариант II Вариант
1. Вычислите площади фигур, ограниченных указанными линиями.
а)![]() ,
, ![]() ,
,
![]() ,
, ![]() ; а)
; а)
![]() ,
, ![]() ,
,
![]() ,
, ![]() ;
;
б)
![]() ,
, ![]() ,
,
![]() ; б)
; б)
![]() ,
, ![]() ,
,
![]() ,
, ![]() ;
;
в)
![]() ,
, ![]() ,
,
![]() ; в)
; в) ![]() ,
, ![]() ,
,
![]() ;
;
г)
![]() ,
, ![]() . г)
. г)
![]() ,
, ![]() .
.
2. Найти объемы тел вращения, образованных вращением вокруг оси Оx площадей, ограниченных линиями.
y2 – 4x = 0, x – 2 = 0, x – 4 = 0, y = 0 y2 – 6x = 0, x – 2 = 0, x – 6 = 0, y = 0
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
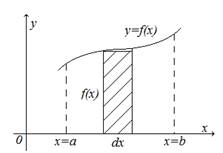
Найдём площадь S криволинейной
трапеции, ограниченной кривой ![]() , осью Ox и двумя прямыми x=a и x=b, где
, осью Ox и двумя прямыми x=a и x=b, где ![]() ,
, ![]() .
.
Так как дифференциал переменной площади S есть площадь
прямоугольника с основанием dx и высотой ![]() ,т.е.
,т.е.
![]() , то интегрируя это равенство в
пределах от a до b, получим
, то интегрируя это равенство в
пределах от a до b, получим 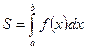 .
.
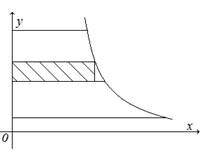
 Если криволинейная
трапеция прилегает к оси Oy так, что
Если криволинейная
трапеция прилегает к оси Oy так, что ![]() ,
,
![]() , то дифференциал переменной
площади S равен
, то дифференциал переменной
площади S равен ![]() , откуда
, откуда 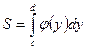 .
.
В том случае, когда криволинейная
трапеция, ограниченная кривой ![]() , осью Ox и прямым
, осью Ox и прямым ![]() и
и ![]() ,
лежит под осью Ox, площадь находится по формуле
,
лежит под осью Ox, площадь находится по формуле 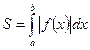 .
.
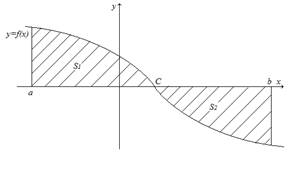
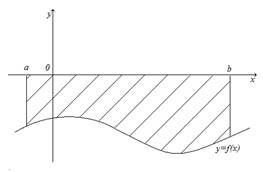
Если
фигура, ограниченная кривой ![]() , осью
Ox и прямыми
, осью
Ox и прямыми ![]() и
и ![]() ,
расположена по обе стороны от оси Ox, то
,
расположена по обе стороны от оси Ox, то 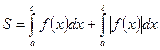 .
.
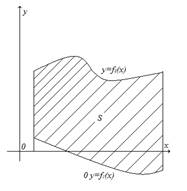
Пусть, наконец, фигура S ограничена двумя
пересекающимися кривыми ![]() и
и ![]() и прямыми
и прямыми ![]() и
и ![]() и
и
![]() . Тогда её площадь находится по
формуле
. Тогда её площадь находится по
формуле 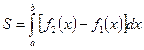 .
.
Объем тела вращения.
 Рассмотрим кривую, заданную уравнением y = f(x).
Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с
основаниями а и b вращать вокруг оси Ох, то получим так называемое тело
вращения.
Рассмотрим кривую, заданную уравнением y = f(x).
Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с
основаниями а и b вращать вокруг оси Ох, то получим так называемое тело
вращения.
Т.к. каждое сечение тела плоскостью x = const
представляет собой круг радиуса ![]() , то объем тела вращения может быть
легко найден по полученной выше формуле:
, то объем тела вращения может быть
легко найден по полученной выше формуле:
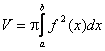
Формулы объемов тел вращения около:
оси Ох 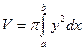 ; оси Оу
; оси Оу 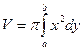
При выполнении практической работы рассмотрите следующие примеры:
Пример 1.
Вычислите площади фигур, ограниченных указанными линиями.
1)
![]() ,
, ![]() ,
,
![]() ,
, ![]()
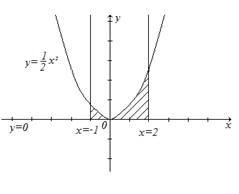 В данном случае
требуется вычислить площадь криволинейной трапеции, ограниченной параболой
В данном случае
требуется вычислить площадь криволинейной трапеции, ограниченной параболой ![]() , прямыми
, прямыми ![]() ,
, ![]() ,
и
,
и ![]() . Посмотрим эти линии.
. Посмотрим эти линии.
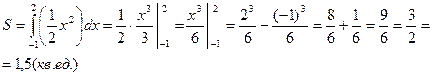
Ответ: 1,5 кв. ед.
2)
![]() ,
, ![]() ,
,
![]() ,
, ![]()
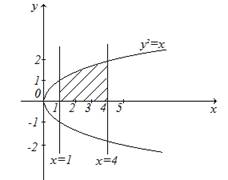
![]()
![]()
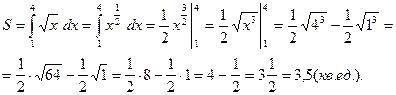
Ответ: 3,5 кв. ед.
3)
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
![]() -парабола
-парабола
![]() -парабола
-парабола
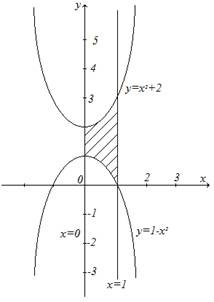
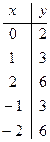
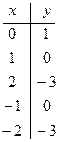
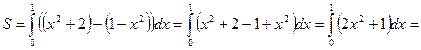
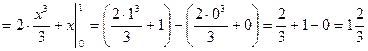 кв. ед.
кв. ед.
Ответ:![]() кв. ед.
кв. ед.
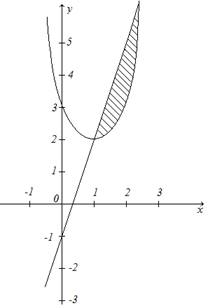 4)
4) ![]() ,
, ![]() .
.
![]() -парабола
-парабола
![]() ,
,
![]() ,
,
(1;2) - вершина параболы
![]()
![]() -прямая
-прямая
![]()
Для нахождения точек пересечения решим систему:
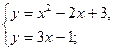
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
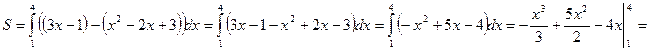
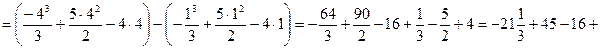
![]() кв.
ед.
кв.
ед.
Ответ: 9,5 кв. ед.
Пример 2.
Вычислить объем тела, образованного вращением вокруг оси Оx площадки, ограниченной линиями y2 = 4x и y = x.
![]()
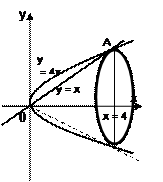 Решение. Решив систему находим точки
пересечения параболы и прямой: О (0; 0) и А (4; 4). Следовательно, пределы
интегрирования a = 0 и b = 4. Объем тела вращения представляет
собой разность объемов параболоида, образованного вращением кривой y2 = 4x (V1) и конуса,
образованного вращением прямой y = x (V2). Тогда
Решение. Решив систему находим точки
пересечения параболы и прямой: О (0; 0) и А (4; 4). Следовательно, пределы
интегрирования a = 0 и b = 4. Объем тела вращения представляет
собой разность объемов параболоида, образованного вращением кривой y2 = 4x (V1) и конуса,
образованного вращением прямой y = x (V2). Тогда
![]()
![]()
![]()
Ответ: ![]() (куб. ед.)
(куб. ед.)
Вопросы для закрепления теоретического материала к практическому занятию:
1.
Какова формула вычисления площади криволинейной трапеции, ограниченой кривой ![]() , осью Ox и прямые
, осью Ox и прямые ![]() и
и ![]() ?
?
2.
Какова формула вычисления полощади криволинейной трапеции, ограниченной кривой ![]() , осью Ox и прямыми
, осью Ox и прямыми ![]() и
и ![]() ,
лежит под осью Ox?
,
лежит под осью Ox?
3.
Какова площадь фигуры ограниченной двумя пересекающимися кривыми ![]() и
и ![]() и
прямыми
и
прямыми ![]() и
и ![]() , где
, где ![]() и
и
![]() ?
?
4.От чего зависит выбор формулы для нахождения объема тела вращения?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Тема практической работы № 5:
Вычисление частных производных и дифференциалов функций нескольких переменных
Цель работы:
применить умения по дифференциальному исчислению функции нескольких действительных переменных
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
I Вариант II Вариант
1. Найдите частные производные функции.
а) ![]() а)
а)
![]()
б) ![]() б)
б)
![]()
в) ![]() в)
в)
![]()
г) ![]() г)
г)
![]()
д) ![]() д)
д)
![]()
е) ![]() е)
е)
![]()
ж) ![]() ж)
ж)
![]()
2. Вычислите значение частной производной функции.
![]() в точке М(-1;2).
в точке М(-1;2). ![]() в точке М(-2;1).
в точке М(-2;1).
3. Вычислите полный дифференциал функции.
![]() в точке М(0;1).
в точке М(0;1). ![]() в точке М(1;0).
в точке М(1;0).
4. Найдите частные производные второго порядка.
![]()
![]()
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Частной
производной функции ![]() по переменной x называется
производная этой функции при постоянном значении переменной y; она обозначается
по переменной x называется
производная этой функции при постоянном значении переменной y; она обозначается
![]() или
или ![]() .
.
Частной
производной функции ![]() по переменной y при постоянном
значении переменной x; она обозначается
по переменной y при постоянном
значении переменной x; она обозначается ![]() или
или ![]() .
.
Частная производная функции нескольких переменных по одной переменной определяется как производная этой функции по соответствующей переменной при условии, что остальные переменные считаются постоянными.
Полным
дифференциалом функции ![]() в некоторой
точке М(x;y) называется
выражение
в некоторой
точке М(x;y) называется
выражение ![]() , где
, где ![]() и
и ![]() вычисляются в точке M(x;y), а
вычисляются в точке M(x;y), а
![]() ,
, ![]() .
.
Если
![]() и
и ![]() имеют
в точке М частные производные по переменным x и y, то они
называются частными производными второго порядка от функции Z(M) в этой точке и
обозначаются:
имеют
в точке М частные производные по переменным x и y, то они
называются частными производными второго порядка от функции Z(M) в этой точке и
обозначаются:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Частные
производные второго порядка вида ![]() ,
, ![]() называются смешанными частными
производными.
называются смешанными частными
производными.
Частные производные третьего порядка определяются как частные производные от частных производных второго порядка и т.д..
При выполнении практической работы рассмотрите следующие примеры:
Пример 1.
Найдите частные производные функции.
а)
![]() ;
;
![]() ;
;
![]() ;
;
б)
![]() ;
;
![]() ;
;
![]() ;
;
в)
![]() ;
;
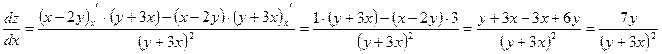
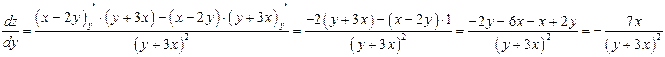 г)
г) ![]()
![]()
![]()
д)
![]()
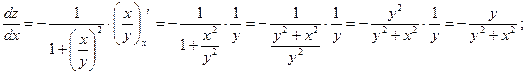
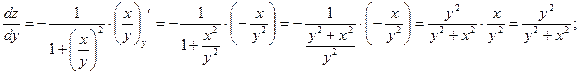
е)
![]() ;
;
![]()
![]()
Пример 2.
Вычислить значение частной производной функции в точке М(-2;-2).
![]()
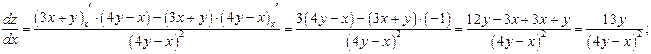
![]()
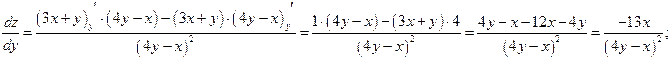
![]()
Пример 3.
Вычислить полный дифференциал функции в точке М(1;1).
![]()
![]()
![]()
![]()
![]()
По
формуле ![]() , получим
, получим ![]() .
.
Пример 4.
Найти частные производные второго порядка функции
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
Вопросы для закрепления теоретического материала к практическому занятию:
1. Что называется частичной производной по переменной x?
2. Что называется частичной производной по переменной y?
3. Что называется полным дифференциалом функции?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Тема практической работы № 6:
Вычисление двойных интегралов.
Цель работы:
применить умения по интегральному исчислению функции нескольких действительных переменных
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
I Вариант II Вариант
1. Вычислите повторные интегралы.
а) 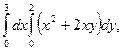 а)
а)
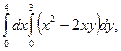
б) 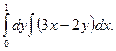 б)
б)
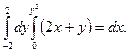
2. Вычислите двойной интеграл по областям, ограниченным указанным линиями.
![]()
![]()
3. Вычислите двойной интеграл по областям, ограниченным указанными линиями, предварительно разбив данную область на 2 области.
![]()
![]()
4. Измените порядок интегрирования в двойном интеграле.
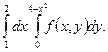
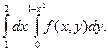
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Двойным интегралом функции f(x;y) по области D называться предел этой суммы:
![]() -
наибольший из диаметров элементарных областей
-
наибольший из диаметров элементарных областей
![]() .
Функция z = f(x;y), для которых
предел существует и конечен, называется интегрируемой в этой области.
.
Функция z = f(x;y), для которых
предел существует и конечен, называется интегрируемой в этой области.
В прямоугольных координатах дифференциал
площади ![]() , тогда двойной интеграл
примет вид
, тогда двойной интеграл
примет вид
![]()
Если f(x;y) > 0, то двойной
интеграл функции ![]() по области D равен объему
тела, органического сверху поверхностью
по области D равен объему
тела, органического сверху поверхностью ![]() ,
сбоку цилиндрической поверхностью,
,
сбоку цилиндрической поверхностью,
образующие которой параллельны оси Oz, а направляющей служит контур фигуры D, и снизу плоскостью z=0.
Основные свойства двойного интеграла.
1) ![]()
2)![]()
3)![]()
 Основные случаи
вычисления двойного интервала в прямоугольных координатах.
Основные случаи
вычисления двойного интервала в прямоугольных координатах.
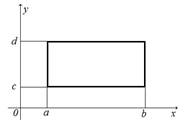
1) Если область D, в которой
рассматривается двойной интеграл, есть прямоугольник со сторонами,
параллельными координатным осям и заданным уравнениями ![]() ,
,![]() , у=с,
, у=с,![]() , то двойной интеграл вычисляется
по одной из формул.
, то двойной интеграл вычисляется
по одной из формул.
![]()
![]()
Интегралы в правых частях формул
называться повторными (или двукратными), а интегралы 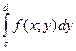 и
и 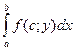 называются внутренними.
называются внутренними.
Под символом 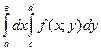 в формуле (1) подразумевается
дважды произведенное интегрирование. Первое интегрирование (внутреннее) по
переменной y совершается в
пределах от с до d в предположении, что x остается
постоянным; результат интегрируется по переменной x в пределах от a до b.
в формуле (1) подразумевается
дважды произведенное интегрирование. Первое интегрирование (внутреннее) по
переменной y совершается в
пределах от с до d в предположении, что x остается
постоянным; результат интегрируется по переменной x в пределах от a до b.
Если вычисление двойное интеграла выполняется по формуле (2), то порядок интегрирования меняется; внутренний интеграл вычисляется по переменной х, причем у сохраняет постоянное значение, а внешнее (повторное) интегрирование производиться по переменной y.
2) Если область D такова, что любая прямая, проходящая внутри этой области и параллельная оси Oy, пересекает ее границу в двух точках, то эта область называется простой относительно оси Ox и определяется системой неравенств вида
![]()
![]()
![]()
В этом случае двойной интеграл выражается через повторный интеграл по формуле.
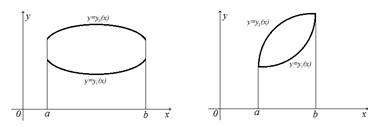
![]() (3)
(3)
3) Если граница области D пересекается в двух точках всякой прямой, проходящей внутри этой области и параллельной оси Oy и определяется системой неравенств вида
![]()
В этом случае двойной интеграл выражается формулой
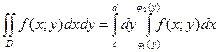 ,
,
где интегрирование сначала выполняется по переменной х, а затем по переменной y.
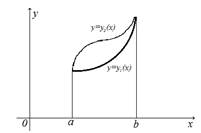
3)Если нижняя или верхняя линии границы состоят из нескольких участков, имеющих различные уравнения, то область D необходимо разбить прямыми, параллельными оси Oy, на такие части, чтобы каждый из участков выражался одним уравнением. В этом случае вычисление двойного интеграла сводиться к вычислению двух (и более) повторных интегралов.
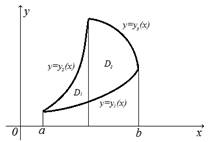 В случае,
изображенном на рисунке, область
В случае,
изображенном на рисунке, область ![]() определяется
системой неравенств
определяется
системой неравенств ![]() а область
а область ![]() - системой неравенств
- системой неравенств ![]() и значит
и значит
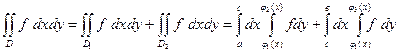 (4).
(4).
При выполнении практической работы рассмотрите следующие примеры:
Пример1.
Вычислите повторный интеграл.
а) 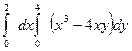 .
.
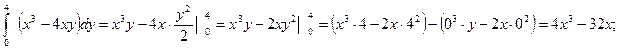
![]()
б) 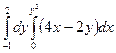
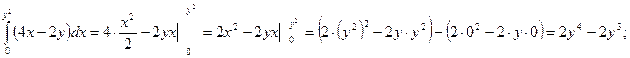
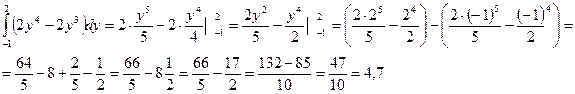
Пример 2.
Вычисление двойной интеграл по областям, ограниченным указанными линиями.
![]()
![]()
![]()
![]()
![]()
Находим точки пересечения этих линий:
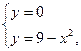
![]()
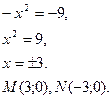
Область D определяется системой неравенств
![]()
![]()
Вычислим двойной интеграл по области D
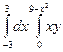
![]()
![]()
![]()
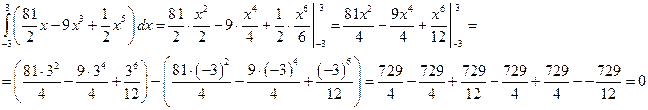
Пример 3.
Вычислите двойной интеграл по областям, ограниченным указанным линиями, предварительно разбив заданную область на 2 области.
![]() ,
, ![]()
![]() ,
,
![]() .
.
Находим точки пересечения этих линий:
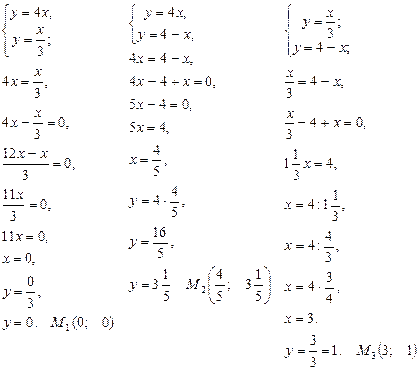
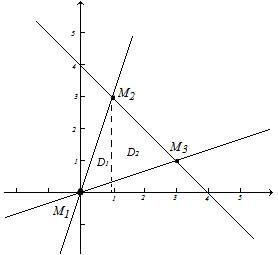
Область D разобьем на две
области ![]() и
и ![]() , которые соответственно
определяются системами неравенств.
, которые соответственно
определяются системами неравенств.
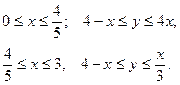
Вычислим двойной интеграл по области ![]() :
:
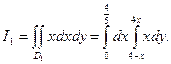
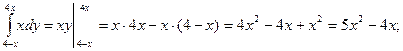
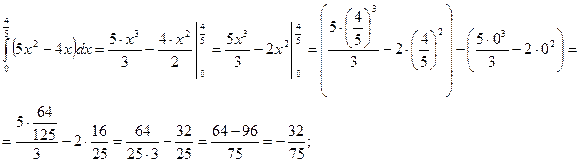
Вычислим двойной интеграл по области![]() :
:
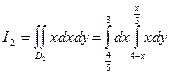
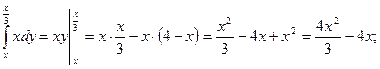
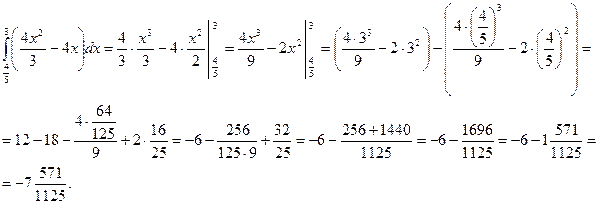
![]()
Пример 4.
Изменить порядок интегрирования в двойном интеграле.
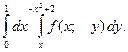
Запишем область интегрирования D в виде системы
неравенств![]() ,
,
Построим линии: ![]()
Найдем точку пересечения линий:
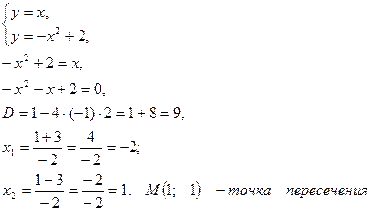
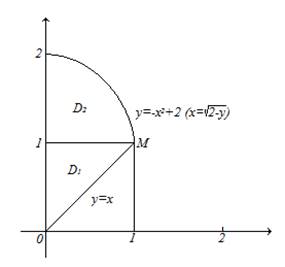
Область D является простой
относительно оси Ox. Рассмотрим область D относительно оси Oy. Через точку M(1; 1), в которой
стыкуются участки верхней границы области D, проведем прямую
параллельную оси Ox эта прямая делить область D на две области ![]() и
и ![]() ,
которые запишем в виде систем неравенств
,
которые запишем в виде систем неравенств ![]()
![]() и
и ![]()
![]()
Тогда согласно формуле 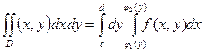 получим
получим
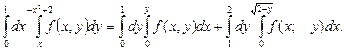
Вопросы для закрепления теоретического материала к практическому занятию:
1. Что называется двойным интегралом?
2.По какой формуле вычисляется двойной интеграл?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Тема практической работы № 7:
Определение сходимости числовых рядов
Цель работы:
применить умения на методы дифференциального исчисления, на определение сходимости числовых рядов.
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
I вариант II вариант
1. Найдите первые четыре члена ряда по заданному общему члену:
а) ![]() а)
а)
![]()
б) ![]() б)
б)
![]()
2. Найдите формулу общего члена ряда:
а) ![]() а)
а)
![]()
б) ![]() б)
б)
![]()
3. Вычислите сумму членов ряда:
![]()
![]()
4. Используя признак сравнения, исследуйте сходимость ряда:
![]()
![]()
5. Используя признак Даламбера, исследуйте сходимость ряда:
![]()
![]()
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Числовым рядом называется сумма вида ![]() , где числа
, где числа
![]() ,
, ![]() ,
,
![]() ,…,
,…,![]() ,…
называемые членами ряда, образуют бесконечную последовательность; член
,…
называемые членами ряда, образуют бесконечную последовательность; член ![]() называется общим членом ряда.
называется общим членом ряда.
Суммы
![]() ,
,
![]() ,
,
![]() ,
,
…………………..
![]() ,
,
составленные из первых членов ряда называются частичными суммами этого ряда.
Каждому
ряду можно сопоставить последовательность частичных сумм ![]() ,
, ![]() ,
,
![]() , …,
, …,![]() ,...
Если при бесконечном возрастании номера n частичная
сумма ряда
,...
Если при бесконечном возрастании номера n частичная
сумма ряда ![]() стремится к пределу S, то ряд называется сходящимся, а число S-суммой
сходящегося ряда, т.е.
стремится к пределу S, то ряд называется сходящимся, а число S-суммой
сходящегося ряда, т.е. ![]() или
или ![]() .
.
Эта
запись равносильна записи ![]()
Если
частичная сумма ![]() ряда при
неограниченном возрастании n не имеет конечного
предела (в частности стремится к
ряда при
неограниченном возрастании n не имеет конечного
предела (в частности стремится к ![]() или к
или к ![]() , то такой ряд называется
расходящимся. Если ряд сходится, то значение
, то такой ряд называется
расходящимся. Если ряд сходится, то значение ![]() при
достаточно большом n является приближенным
выражением суммы ряда S.
при
достаточно большом n является приближенным
выражением суммы ряда S.
Разность
![]() называется остатком ряда. Если ряд
сходится, то его остаток стремится к нулю, т.е.
называется остатком ряда. Если ряд
сходится, то его остаток стремится к нулю, т.е. ![]() , и наоборот, если остаток
стремится к нулю, то ряд сходится.
, и наоборот, если остаток
стремится к нулю, то ряд сходится.
Ряд
вида ![]() называется
гармоническим.
называется
гармоническим.
Ряд
![]() может сходиться только при
условии, что его общий член
может сходиться только при
условии, что его общий член ![]() при
неограниченном увеличении номера n стремится к нулю:
при
неограниченном увеличении номера n стремится к нулю: ![]()
Если
![]() , то ряд
, то ряд ![]() расходится – это достаточный
признак расходимости ряда.
расходится – это достаточный
признак расходимости ряда.
1. Признак сравнения рядов с положительными членами.
Исследуемый ряд сходится, если его члены не превосходят соответствующих членов другого, заведомо сходящегося ряда; исследуемый ряд расходится, если его члены превосходят соответствующие члены другого, заведомо расходящегося ряда.
При
исследовании рядов на сходимость и расходимость по этому признаку часто
используется геометрический ряд ![]() ,
который сходится при
,
который сходится при ![]() и расходится
при
и расходится
при ![]() и гармонический ряд
и гармонический ряд ![]() являющийся расходящимся.
являющийся расходящимся.
При
исследовании рядов используется также обобщённый гармонический ряд ![]()
Если р=1, то данный ряд обращается в гармонический ряд, который является расходящимся.
Если
p<1 , то члены данного ряда больше
соответствующих членов гармонического ряда и, значит, он расходится. При p>1 имеем геометрический ряд, в котором ![]() он является сходящимся. Итак,
обобщённый гармонический ряд сходится при p>1 и
расходится при
он является сходящимся. Итак,
обобщённый гармонический ряд сходится при p>1 и
расходится при ![]() .
.
2. Признак Даламбера.
Если
для ряда с положительными членами ![]() выполняется
условие
выполняется
условие ![]() , то сходится при
, то сходится при ![]() и расходится при
и расходится при ![]() .
.
Признак Даламбера не даёт ответа, если ![]() . В этом случае для исследования
ряда применяются другие приёмы.
. В этом случае для исследования
ряда применяются другие приёмы.
При выполнении практической работы рассмотрите следующие примеры:
Пример 1.
Найдите первые четыре члена ряда по заданному общему члену:
![]()
![]()
![]()
![]()
![]()
Пример 2.
Найдите формулу общего члена ряда:
![]()
Числители
членов ряда образуют натуральный ряд чисел, а соответствующие им знаменатели –
натуральный ряд чисел, начиная с 3. Знаки чередуются по закону ![]() или по закону
или по закону ![]() . Значит, n-й
член ряда имеет вид
. Значит, n-й
член ряда имеет вид
![]() или
или
![]()
Пример 3.
Вычислите сумму членов ряда.
![]()
Находим частичные суммы членов ряда:
![]()
![]()
![]()
![]()
………………………………………………….
Общий член этой последовательности:
![]()
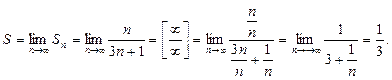
Последовательность
частных сумм имеет предел, равный ![]() . Итак,
ряд сходится и
. Итак,
ряд сходится и ![]() .
.
Пример 4.
Используя признак сравнения, исследуйте сходимость ряда:
а)
![]()
![]()
Необходимый признак сходимости ряда выполняется.
Сравним
данный ряд с геометрическим рядом ![]() ,
который сходится, так как
,
который сходится, так как ![]() .
.
Сравнивая
члены данного ряда, начиная со второго, с соответствующими членами
геометрического ряда, получим неравенства ![]() т.е. члены данного ряда, начиная со
второго, соответственно меньше членов геометрического ряда, откуда следует, что
данный ряд сходится.
т.е. члены данного ряда, начиная со
второго, соответственно меньше членов геометрического ряда, откуда следует, что
данный ряд сходится.
б)
![]()
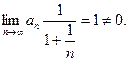
Здесь выполняется достаточный признак расходимости ряда, следовательно ряд расходится. При сравнении данного ряда с гармоническим также убеждаемся, что ряд расходится.
![]()
Пример 5.
Исследовать сходимость ряда, используя признак Даламбера:
а)
![]()
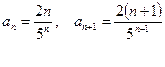
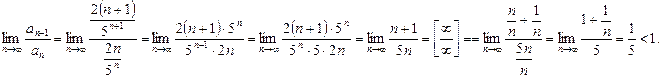
Следовательно, данный ряд сходится.
б)
![]()
![]()
![]()
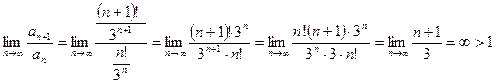 , т.е. ряд расходится.
, т.е. ряд расходится.
Вопросы для закрепления теоретического материала к практическому занятию:
1. Что называется числовым рядом?
2. Какой ряд называется расходящимся?
3. Какой ряд называется сходящимся?
4. Какой ряд называется геометрическим?
5. Какой ряд называется гармоническим?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Тема практической работы № 8:
Решение дифференциальных уравнений
Цель работы:
применить умения по решению дифференциальных уравнений
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
I Вариант II Вариант
![]()
![]()
2. Решите однородное дифференциальное уравнение первого порядка.
![]()
![]()
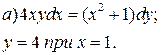
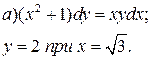
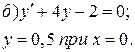
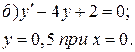
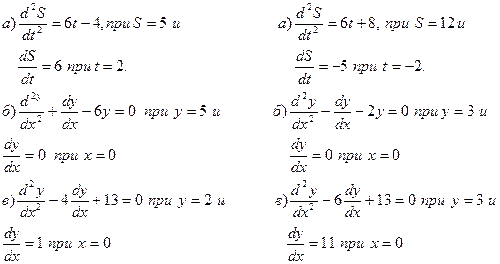
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию у и ее производное или дифференциалы.
Символически дифференциальное уравнение
записывается так: ![]()
![]() .
.
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Порядком дифференциального уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.
Решением (или интегралом) дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Общим решением (или общим интегралом) дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значимых произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных значениях аргумента или функции.
График частного решения дифференциального уравнения называется интегральной кривой.
Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.
Дифференциальным уравнениям первого порядка называются уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
Дифференциальным уравнением с разделяющимися переменными называются уравнения вида
![]()
Для решения этого уравнения нужно сначала разделить переменные:
![]() , а
затем проинтегрировать обе части полученного равенства:
, а
затем проинтегрировать обе части полученного равенства:
![]()
Уравнения вида ![]() называется однородным, если
называется однородным, если ![]() и
и![]() -однородные
функции одного измерения.
-однородные
функции одного измерения.
Функция ![]() называется однородной измерения m , если
называется однородной измерения m , если ![]() и
и![]() и
и![]()
С помощью подстановки ![]() однородное уравнение приводится к
уравнению с разделяющимися переменными.
однородное уравнение приводится к
уравнению с разделяющимися переменными.
Уравнение вида ![]() где
где![]()
![]() и
и ![]() -
функции от х, называется линейным дифференциальным уравнением первого
порядка. В частном случае
-
функции от х, называется линейным дифференциальным уравнением первого
порядка. В частном случае ![]() и
и ![]() могут быть постоянными величинами.
могут быть постоянными величинами.
Это уравнение приводит к уравнению с
разделяющимися переменными с помощью подстановки ![]() ,
где и
,
где и ![]() - новые функции от
- новые функции от ![]() .
.
Уравнение, содержащие производные (или дифференциалы) не выше второго порядка, называется дифференцированным уравнением второго порядка. В общем виде уравнение второго порядка записывается следующим образом:
![]()
Общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
![]() (1)
(1)
где p и q – постоянные величины.
Для
отыскания общего решения уравнения (1) заменой ![]() на соответствующие степени
на соответствующие степени ![]() причем сама функция
причем сама функция ![]() заменяется единицей.
заменяется единицей.
Тогда
общее решение дифференциального уравнения строится в зависимости от корней ![]() и
и ![]() характеристического
уравнения. Здесь возможны три случая.
характеристического
уравнения. Здесь возможны три случая.
I
случай. Корни ![]() и
и ![]() - действительны и различные. В этом
случае общее решение уравнения (1) имеет вид:
- действительны и различные. В этом
случае общее решение уравнения (1) имеет вид:
![]() (3)
(3)
II случай. Корни ![]() и
и ![]() -
действительные и равные:
-
действительные и равные: ![]() Тогда
общее решение уравнение (1) записывается так:
Тогда
общее решение уравнение (1) записывается так:
![]() (4)
(4)
III случай. Корни ![]() и
и ![]() -
комплексно-сопряженные:
-
комплексно-сопряженные: ![]() В
этом случае общее решение уравнения (1) записывается следующим образом:
В
этом случае общее решение уравнения (1) записывается следующим образом:
![]() (5)
(5)
При выполнении практической работы рассмотрите следующие примеры:
Пример 1.
Найдите общее решение уравнений с разделяющимися переменными.
а)
![]()
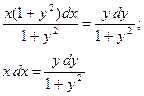
![]()
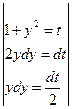 ;
;
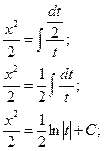
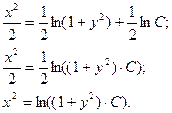
б) ![]()
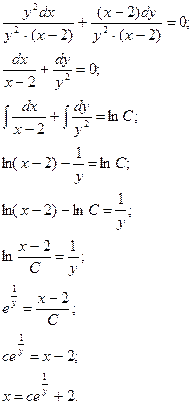
Пример 2.
Решите однородное дифференциальное уравнение первого порядка.
![]()
![]()
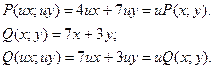
Замена:
![]()
![]()
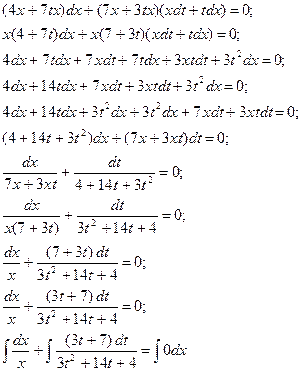
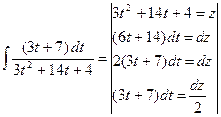 =
=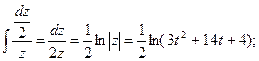
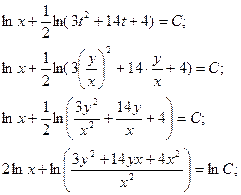
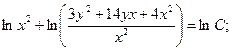
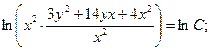
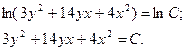
Пример 3.
Решите линейное дифференциальное уравнение первого порядка.
![]() -
- ![]() -
3 =0;
-
3 =0;
Положим
![]() . Продифференцируем по
. Продифференцируем по ![]() :
: ![]() =
=![]() +
+ ![]() .
.
Подставим эти выражения в уравнения, получим:
![]() +
+ ![]() -
- ![]() ;
;
![]() +
+ ![]() -
- ![]() -3=0;
(*)
-3=0;
(*)
![]() -
- ![]() ;
;
![]() -
- ![]() ;
;
![]() =
=![]() ;
;
![]() =
= ![]() ;
;
![]()
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
Подставим
теперь выражение для ![]() в уравнение
(*), тогда получим уравнение
в уравнение
(*), тогда получим уравнение
![]()
![]() -3=0;
-3=0;
![]()
![]() =3;
=3;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Зная
![]() и
и ![]() ,
теперь получаем общее решение данного уравнения:
,
теперь получаем общее решение данного уравнения:
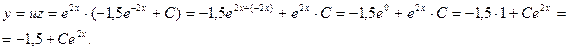
Пример 4.
Найдите частные решения дифференциальных уравнений.
![]()
![]()
![]()
![]()
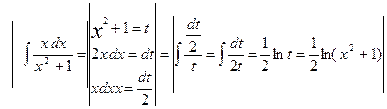
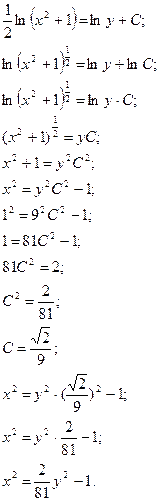
б)
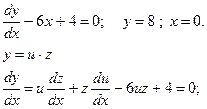
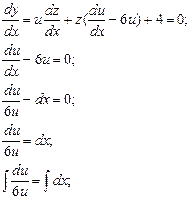
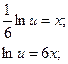
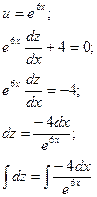
![]()
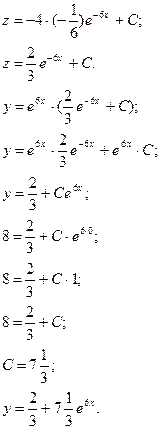
Пример 5.
Найдите частное решение уравнения, удовлетворяющее указанным начальным условием.
![]()
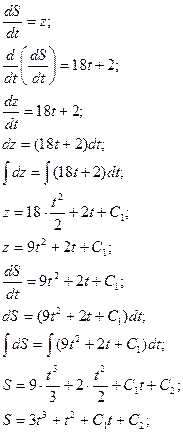
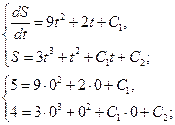
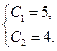
![]()
Пример 6.
Найдите частные решения дифференциальных уравнений.
а)
![]() при
при ![]() при
при ![]() .
.
Составим характеристическое уравнение и найдите его корни.
![]()
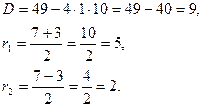
Так как корни характеристического уравнения действительны и различны, то общее решение данного дифференциального уравнения согласно формуле (3) запишется так:
![]()
Для
нахождения искомого частного решения нужно определить значения постоянных С1
и С2. Подставив в общее решение значения ![]() получим:
получим:
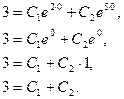
Продифференцировав
общее решение и подставив в полученное выражение ![]() , имеем:
, имеем:
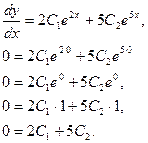
![]()
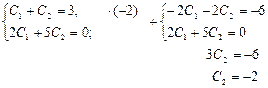
![]()
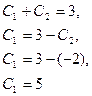
Таким образом, искомое частное решение имеет вид
![]()
б)
![]() .
.
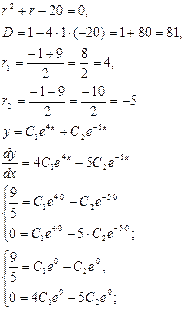
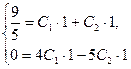
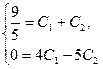
![]()
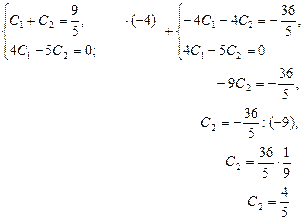
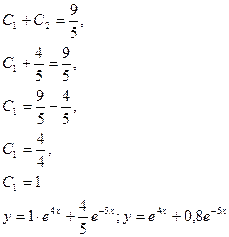
Вопросы для закрепления теоретического материала к практическому занятию:
1. Что называется дифференциальным уравнением?
2. Что называется решением дифференциального уравнения?
3. Что называется частными решениями дифференциального уравнения?
4. Какой вид имеет дифференциальное уравнение с разделяющимися переменными?
5. Какой вид имеет однородное дифференциальное уравнение?
6. Какой вид имеет линейное дифференциальное уравнение первого порядка.
7. Какое уравнение называется дифференциальным уравнением второго порядка?
8. Какой общий вид уравнения второго порядка?
9. какой общий вид линейного однородного дифференциального уравнения второго порядка с постоянным коэффициентами?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Тема практической работы № 9:
Нахождение обратной матрицы
Цель работы:
применить умения по линейной алгебре: выполнять операции над матрицами.
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
I вариант II вариант
1. Найти обратную матрицы с помощью формулы.
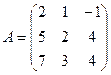
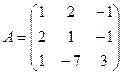
2.Найдите обратную матрицу с помощью элементарный преобразований.
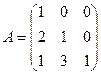
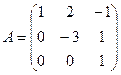
3. Найдите обратную матрицу
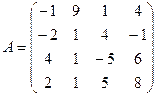
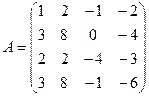
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Для каждого числа ![]() существует обратное число
существует обратное число ![]() такое, что произведение
такое, что произведение ![]() .
.
Матрица ![]() называется обратной по отношению к
квадратной матрице
называется обратной по отношению к
квадратной матрице ![]() , если при
умножении этой матрицы на данную как справа, так и слева получается единичная
матрица:
, если при
умножении этой матрицы на данную как справа, так и слева получается единичная
матрица: ![]() . Только квадратная
матрица имеет обратную; в этом случае и обратная матрица является матрицей того
же порядка.
. Только квадратная
матрица имеет обратную; в этом случае и обратная матрица является матрицей того
же порядка.
Не каждая
квадратная матрица имеет обратную. Для существования матрицы ![]() необходимым и достаточным условием
является требование
необходимым и достаточным условием
является требование ![]() .
.
Если определитель
матрицы отличен от нуля (![]() ), то
такая квадратная матрица называется невырожденной, или неособенной; в противном
случае (при
), то
такая квадратная матрица называется невырожденной, или неособенной; в противном
случае (при ![]() ) – вырожденной, или
особенной.
) – вырожденной, или
особенной.
Обратная матрица ![]() существует (и единственна) тогда и
только тогда, когда исходная матрица невырожденная.
существует (и единственна) тогда и
только тогда, когда исходная матрица невырожденная.
Алгоритм вычисления обратной матрицы.
1) Находим
определитель исходной матрицы. Если ![]() , то
матрица
, то
матрица ![]() вырожденная и обратной
матрицы
вырожденная и обратной
матрицы ![]() не существует.
не существует.
Если ![]() , то матрица
, то матрица ![]() невырожденная и обратная матрица
существует.
невырожденная и обратная матрица
существует.
2) Находим матрицу ![]() , транспонированную к
, транспонированную к ![]() .
.
3) Находим
алгебраические дополнения элементов транспонированной матрицы и составляем из
них присоединенную матрицу ![]() .
.
4) Вычисляем матрицу
по формуле: ![]()
Любую
невырожденную квадратную матрицу ![]() с
помощью отдельных элементарных преобразований только строк или только столбцов
можно привести к единичной матрице
с
помощью отдельных элементарных преобразований только строк или только столбцов
можно привести к единичной матрице ![]() того
же порядка. При этом те же преобразования, совершенные над матрицей
того
же порядка. При этом те же преобразования, совершенные над матрицей ![]() в том же порядке, приводят ее к
обратной матрице
в том же порядке, приводят ее к
обратной матрице ![]() . На этом
основан ещё один способ нахождения обратной матрицы. Удобно совершать
элементарные преобразования над матрицами
. На этом
основан ещё один способ нахождения обратной матрицы. Удобно совершать
элементарные преобразования над матрицами ![]() и
и
![]() одновременно, записывая их рядом
через черту.
одновременно, записывая их рядом
через черту.
При выполнении заданий рассмотрите примеры.
Пример 1.
Найти матрицу, обратную к данной:
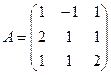
1) Находим
определитель матрицы ![]() .
.
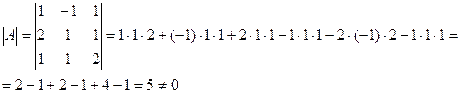
Т.к. ![]() , то матрица
, то матрица ![]() невырожденная и обратная матрица
невырожденная и обратная матрица ![]() существует.
существует.
2) Находим
транспонированную к ![]() матрицу
матрицу ![]() .
.
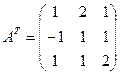
3) Находим
алгебраические дополнения элементов матрицы ![]() и
составляем из них присоединенную матрицу
и
составляем из них присоединенную матрицу ![]() .
.
![]() ;
; ![]()
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
![]() .
.
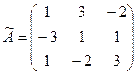 .
.
4) Вычислим по
формуле обратную матрицу ![]() .
.
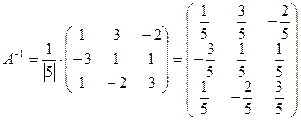 .
.
Пример 2.
Найти матрицу,
обратную к матрице ![]() , преобразуя
исходную матрицу в единичную
, преобразуя
исходную матрицу в единичную ![]() .
.
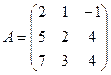 .
.
∙(-6) ∙(-6)
Следовательно,
матрица
![]() имеет обратную
имеет обратную
![]()
![]()
![]()
∙(-1) ∙(-1)
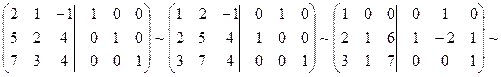
![]()
![]()
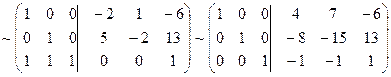
Слева получим
единичную матрицу. Найденная справа от черты квадратная матрица является
обратной к исходной матрице ![]() :
:
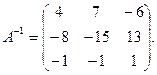
Вопросы для закрепления теоретического материала к практическому занятию:
1. Какая матрица называется обратной?
2. Сформулировать необходимое и достаточное условие существования обратной матрицы?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Тема практической работы № 10:
Решение системы линейных уравнений по формулам Крамера, методом Гаусса и с помощью обратной матрицы
Цель работы:
применить умения по линейной алгебре: решать системы линейных уравнений.
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
I вариант II вариант
1.Решите систему уравнений по правилу Крамера.
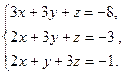
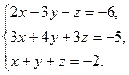
![]() 2.Решите систему уравнений
матричным методом.
2.Решите систему уравнений
матричным методом.
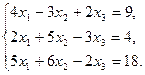
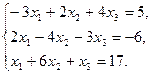
3. Решите систему линейных уравнений методом Гаусса.
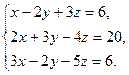
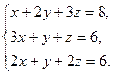
4.Решите систему
линейных уравнений любым способом.![]()
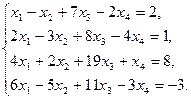
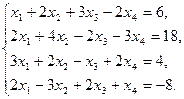
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Пусть дана система n алгебраических уравнений с n неизвестными видами.
![]()
![]()
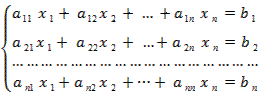
или в матричной форме AX = b, где
A= 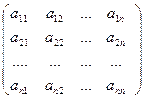 - матрица системы,
- матрица системы,
X=![]() - матрица –
столбец неизвестных,
- матрица –
столбец неизвестных,
B = ![]() - матрица –
столбец свободных членов данной системы.
- матрица –
столбец свободных членов данной системы.
Правило Крамера.
Если в системе ∆ ≠ 0 , т.е. матрица А невырожденная и имеет единственное решение.
X = A-1 ·В, или x![]() =
= ![]() , i = 1,2,…,n, где
, i = 1,2,…,n, где ![]() – определитель, получаемый из
определителя ∆ системы заменой i – го столбца на
столбец свободных членов.
– определитель, получаемый из
определителя ∆ системы заменой i – го столбца на
столбец свободных членов.
Метод Гаусса
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних
(по номеру) переменных, находятся все остальные переменные.
При выполнении заданий рассмотрите примеры.
Пример 1.
Решить систему уравнений по правилу Крамера.
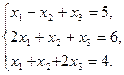
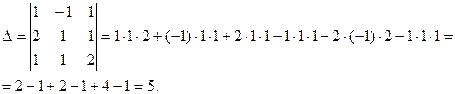
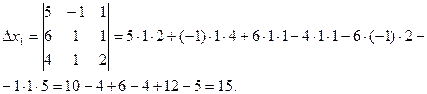
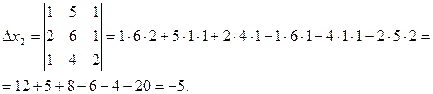
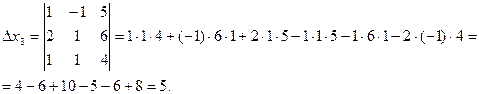
Тогда
![]()
![]()
![]()
Ответ: (3;-1;1).
Пример 2.
Решите систему линейных алгебраических уравнений матричным способом.
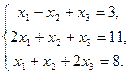
A =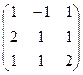 -
матрица системы уравнений,
-
матрица системы уравнений,
X = ![]() - матрица –
столбец неизвестных,
- матрица –
столбец неизвестных,
B= ![]() – матрица – столбец свободных
членов данной системы.
– матрица – столбец свободных
членов данной системы.
Тогда
в матричной форме данная система будет иметь вид: АX = B. Найдем
определитель матрицы ![]() .
.
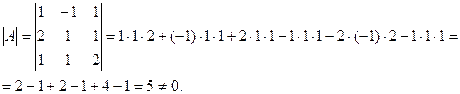
Так
как ![]() ≠ 0, то матрица A невырожденная, и
существует обратная матрица А -1.
≠ 0, то матрица A невырожденная, и
существует обратная матрица А -1.
Обратную матрицу А-1 находим по формуле:
![]()
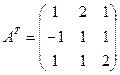
Находим
алгебраические дополнения элементов матрицы AТ и составляем из
них присоединенную матрицу ![]() .
.
A11 = (-1)1+1 ![]() = 2-1=1;
A21 = (-1)2+1
= 2-1=1;
A21 = (-1)2+1
![]() = - (4-1) = -3;
= - (4-1) = -3;![]()
A12 = (-1)1+2 ![]() =
-(-2-1)=3; A22 = (-1)2+2
=
-(-2-1)=3; A22 = (-1)2+2 ![]() = 2 – 1 = 1;
= 2 – 1 = 1;
A13 = (-1)1+3 ![]() = -1-1=-2;
A23 = (-1)2+3
= -1-1=-2;
A23 = (-1)2+3 ![]() = - (-1-2) = 1;
= - (-1-2) = 1;
A31 = (-1)3+1 ![]() = 2-1 = 1;
A33 = (-1)3+3
= 2-1 = 1;
A33 = (-1)3+3 ![]() = 1+2=3.
= 1+2=3.
A32 = (-1)3+2 ![]() = -(1+1) = -2;
= -(1+1) = -2;
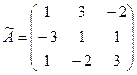 .
.
A-1 = ![]() ·
· 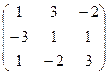 и решение системы найдем по формуле
и решение системы найдем по формуле
X = A-1 · В, т.е.
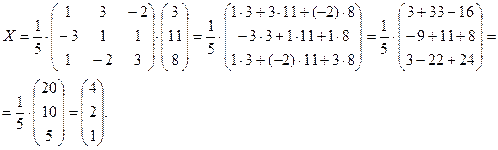
Ответ: (4;2;1)
Пример 3.
Решите систему методом Гаусса.
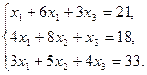
![]()
![]()
![]()
![]()
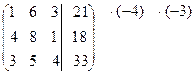
![]()
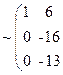
![]()
![]()
![]()
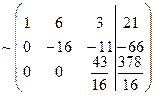 .
.
Получаем систему уравнений:
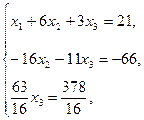 ;
; 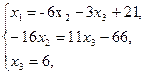
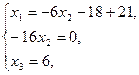
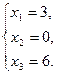
Ответ: (3;0;6)
Пример 4.
Методом Гаусса решите систему уравнений
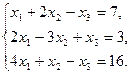
![]()
![]()
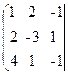
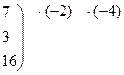
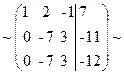
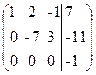
И так, уравнение, соответствующее третьей строке последней матрицы, противоречиво, т.к. в результате преобразований получено неверное равенство: 0= -1, следовательно, данная система несовместная.
Ответ: нет решений.
Вопросы для закрепления теоретического материала к практическому занятию:
1. Что называется решением системы линейных уравнений?
2. Какая система уравнений называется совместной?
3. Какими способами можно решить системы линейных уравнений?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Тема практической работы № 11:
Решение задач по аналитической геометрии
Цель работы:
применить умения по решению задач, используя уравнения прямых и кривых второго порядка на плоскости.
Оборудование:
1. Рабочая тетрадь в клетку.
2. Раздаточный материал: инструкционные карты-20шт.
3. Калькулятор простой.
Задание:
I Вариант
1. Построить прямые
а) ![]()
б) ![]()
в) ![]()
г) ![]()
2. Составьте уравнение прямой, проходящей через данную точку Мо и перпендикулярной данному вектору n: М0(-2;3), n=(4;-5).
3. На прямой ![]() найдите
точку равноудаленную от точек: А(5;1) и В(2;-4)
найдите
точку равноудаленную от точек: А(5;1) и В(2;-4)
4. Составьте уравнение прямой в отрезках на осях, если она пересекает оси координат в точках: А(-2;0) и В(0;3).
5. Составьте уравнение прямой, проходящей через точку (-1;1) и имеющей угловой коэффициент k=1.
6. Составьте уравнение прямой, проходящей через две точки: А(-3;-2), В(1;5).
7. Стороны АВ, ВС и АС треугольника АВС
даны соответственно уравнениями ![]() Определить координаты его вершин.
Определить координаты его вершин.
8. Даны вершины ![]() треугольника АВС. Составить
уравнения медианы, высоты и биссектрисы, проведенных из вершины
А.
треугольника АВС. Составить
уравнения медианы, высоты и биссектрисы, проведенных из вершины
А.
7. Найдите центр и радиус окружности и
постройте ее ![]()
8. Найдите вершины, фокусы, эксцентриситет, асимптоты гиперболы:
![]()
9. Построите параболу: ![]()
II Вариант
1. Построить прямые
а) ![]()
б) ![]()
в) ![]()
г) ![]()
2. Составьте уравнение прямой, проходящей через данную точку Мо и перпендикулярной данному вектору n:
М0(1;-1), n=(-3;4)
3. На прямой ![]() найдите точку равноудаленную от
точек: А(-8;-3) и В(-5;6).
найдите точку равноудаленную от
точек: А(-8;-3) и В(-5;6).
4. Составьте уравнение прямой в отрезках на осях, если она пересекает оси координат в точках: А(3;0) и В(0;-4).
5. Составьте уравнение прямой, проходящей через точку (2;0) и имеющей угловой коэффициент k=-2.
6. Составьте уравнение прямой, проходящей через две точки: А(-1;-3), В(3;5)
7. Стороны АВ, ВС и АС треугольника АВС даны соответственно уравнениями
![]() Определить координаты его вершин.
Определить координаты его вершин.
8. Даны вершины треугольника АВС: ![]() . Составить уравнения медианы,
высоты и биссектрисы, проведенных из вершины А.
. Составить уравнения медианы,
высоты и биссектрисы, проведенных из вершины А.
7. Найдите центр и радиус окружности и
постройте ее ![]()
8. Найдите вершины, фокусы, эксцентриситет, асимптоты гиперболы:
![]()
9. Построите параболу: ![]()
Порядок выполнения:
1. Внимательно прочитать тему и цель практической работы.
2. Изучить учебный материал по теме.
3. Ответить на вопросы.
4. Выполнить задания.
5. Подготовить отчет.
Пояснения к работе (учебный материал):
Уравнение
первой степени относительно x и
y, т.е. уравнение вида ![]() при условии, что коэффициенты A и B одновременно не
равны нулю, называется общим уравнением прямой.
при условии, что коэффициенты A и B одновременно не
равны нулю, называется общим уравнением прямой.
Частные случаи общего уравнения прямой.
|
Значение коэффициента |
Вид уравнения |
Положение прямой |
|
|
|
Проходит через начало координат |
|
|
|
Параллельна оси Oх |
|
|
|
Параллельна оси Oу
|
|
|
|
Совпадает с осью Ох
|
|
|
|
Совпадает с осью Оу |
![]() – каноническое уравнение прямой.
– каноническое уравнение прямой.
![]() - равнение прямой
в отрезках на осях где a и b – соответственно
абсцисса и ордината точек пересечения прямой с осями Ох и Оу.
- равнение прямой
в отрезках на осях где a и b – соответственно
абсцисса и ордината точек пересечения прямой с осями Ох и Оу.
![]() – уравнение прямой
с угловым коэффициентом, где
– уравнение прямой
с угловым коэффициентом, где ![]() –
угловой коэффициент.
–
угловой коэффициент.
![]() – уравнение
прямой, проходящей через данную точку
– уравнение
прямой, проходящей через данную точку ![]() в
заданном направлении, где
в
заданном направлении, где ![]() –
угловой коэффициент прямой.
–
угловой коэффициент прямой.
![]() – уравнение
прямой, проходящей через две точки
– уравнение
прямой, проходящей через две точки ![]() и
и ![]() .
.
Окружность.
Окружностью называется множество всех точек плоскости, равноудалённых от данной точки этой плоскости, называемой центром.
Уравнение окружности с центром в начале
координат и радиусом r имеет вид ![]() .
.
Уравнение окружности с центром в точке О1(а;b) и радиусом r имеет вид ![]() .
.
Уравнение окружности в общем виде записывается так:
![]() , где А,В,С,D – постоянные
коэффициенты.
, где А,В,С,D – постоянные
коэффициенты.
Гипербола.
Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (2а), меньшая расстояния между фокусами (2с).
Уравнение гиперболы, фокусы
которой лежат на оси Ох, имеет вид ![]() , где а – длина действительной
полуоси, b – длина мнимой
полуоси.
, где а – длина действительной
полуоси, b – длина мнимой
полуоси.
Зависимость между параметрами a,b,c выражается
соотношением ![]() .
.
Эксцентриситетом гиперболы называется отношение фокусного расстояния к ее действительной оси:
![]() .
.
Гипербола имеет две асимптоты, уравнения
которых ![]() .
.
Если действительная и мнимая оси гиперболы
равны (т.е. a=b), то гипербола
называется равносторонне. Уравнение равносторонней гиперболы записывается в
виде ![]() , а уравнения ее
асимптоты
, а уравнения ее
асимптоты ![]() .
.
Если фокусы гиперболы лежат на оси Оу,
то ее уравнение имеет вид ![]() , или
, или ![]() , а уравнения асимптоты такой
гиперболы
, а уравнения асимптоты такой
гиперболы ![]() .
.
Уравнения равносторонней гиперболы с
фокусом на оси Оу имеет вид ![]() .
.
Парабола с вершиной в начале координат.
Параболой называется множество точек на плоскости, равноудаленных от данной точки, называемой директрисой.
Уравнение параболы с вершиной в начале
координат, осью симметрии которой служит ось Ох и ветви направлены
вправо, имеет вид ![]() , где р>0
(параметр параболы) – расстояние от фокуса до директрисы.
, где р>0
(параметр параболы) – расстояние от фокуса до директрисы.
Уравнение параболы с вершиной в начале
координат, осью симметрии которой служит ось Ох и ветви направлены
влево, имеет вид ![]() (р>0)
(р>0)
Уравнение ее директрисы ![]() .
.
Уравнение параболы с вершиной в начале
координат, осью симметрии которой служит ось Оу и ветви направлены
вверх, имеет вид ![]() (р>0)
(р>0)
Уравнение ее директрисы ![]() .
.
Уравнение параболы с вершиной в начале
координат осью симметрии которой служит ось Оу и ветви направлены вниз,
имеет вид ![]() (р>0).
(р>0).
Уравнение параболы с вершиной в точке (а;b), с осью симметрии,
параллельной оси Ох, и ветвями, направленными вправо имеет вид ![]() .
.
Уравнение параболы с вершиной в точке (а;b), с осью симметрии,
параллельной оси Ох, и ветвями, направленным влево, имеет вид ![]() .
.
Уравнение параболы с вершиной в точке (а;b), с осью симметрии,
параллельной оси Оу, и ветвями, направленным вверх, имеет вид ![]() .
.
Уравнение параболы с вершиной в точке (а;b), с осью симметрии,
параллельной оси Ох, и ветвями, направленным вниз, имеет вид ![]() .
.
В каждом из уравнений параметр параболы p>0 – расстояние от фокуса параболы до ее директрисы.
При выполнении
заданий рассмотрите примеры:![]()
Пример 1.
Построить прямые: а) ![]() , б)
, б) ![]() ,
в)
,
в) ![]() .
.
Решение.
а) Найдите координаты точек пересечения с осями Ох и Оу.
Полагая ![]() ,
получим
,
получим
![]() ,
,
![]() ,
,
![]() .
.
![]() .
.
При х=0, получим
![]() ,
,
![]() ,
,
![]() .
.
![]()
Через точки А и В проводим искомую прямую.
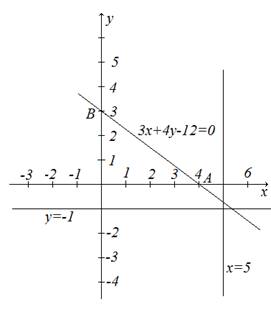
б) На оси Ох возьмем точку![]() . Через эту точку проведём прямую,
параллельную оси Оу.
. Через эту точку проведём прямую,
параллельную оси Оу.
в) На оси Оу возьмем точку![]() . Через эту точку проводим прямую,
параллельную оси Ох.
. Через эту точку проводим прямую,
параллельную оси Ох.
Пример 2.
Составить уравнение прямой, проходящей
через точку ![]() и перпендикулярной
вектору
и перпендикулярной
вектору ![]() .
.
Решение.
Пусть ![]() – произвольная точка искомой прямой.
Вектор
– произвольная точка искомой прямой.
Вектор ![]() перпендикулярен вектору
перпендикулярен вектору ![]() . Так как векторы перпендикулярны, то их
скалярное произведение равно нулю:
. Так как векторы перпендикулярны, то их
скалярное произведение равно нулю:![]() .
Записав произведение этих векторов в координатной форме, получим
.
Записав произведение этих векторов в координатной форме, получим
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
Ответ: ![]() .
.
Пример 3.
На прямой ![]() найти
точку М, равноудаленную от точек
найти
точку М, равноудаленную от точек ![]() и
и
![]()
Решение.
Обозначим
координаты точки М через ![]() ,
получим:
,
получим:
![]()
![]()
Приравняем правые части уравнений.
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Точка ![]() принадлежит
прямой
принадлежит
прямой ![]() , следовательно, ее
координаты удовлетворяют этому уравнению.
, следовательно, ее
координаты удовлетворяют этому уравнению.
Решаем систему уравнений
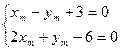
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ответ: ![]()
Пример 4.
Построить прямую ![]()
Решение. Перепишем уравнение так: ![]() , т.е.
, т.е. ![]() и
и
![]() . Таким образом, получаем точки
. Таким образом, получаем точки ![]() и
и ![]() . Строим
прямую, проходящую через точки А и В.
. Строим
прямую, проходящую через точки А и В.
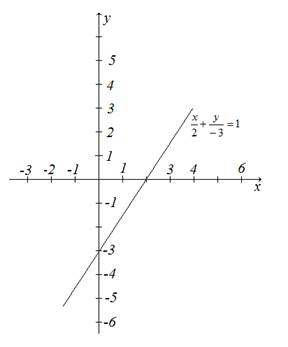
Пример 5.
Составим уравнение прямой пересекающей ось
Ох в точке ![]() , а ось ординат
– в точке
, а ось ординат
– в точке ![]() .
.
Решение.
![]() и
и ![]() . Следовательно,
. Следовательно, ![]() .
.
Ответ: ![]() .
.
Пример 6.
Составить уравнение прямой, проходящей
через точку ![]() и имеющей угловой
коэффициент
и имеющей угловой
коэффициент ![]()
Решение.
![]() ,
, ![]() ,
, ![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ответ: ![]() .
.
Пример 7.
Составить уравнение прямой, проходящей через точки А(2;-3) и В(-1;4).
Решение.
![]() ,
, ![]() ,
, ![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ответ: ![]() .
.
Пример 8.
Определить, какие из точек М1(3;1), М2(2;3), М3(6;3), М4(-3;-3),М5(3;-1),М6(-2;1) лежат на прямой L: 2х-3у-3=0 и какие не лежат на ней.
Решение.
Для того, чтобы определить, какие из точек лежат на данной прямой и какие не лежат на ней, надо подставить координаты данных точек в уравнение; если получим верное равенство, то точки лежат на прямой, в противном случае – нет.
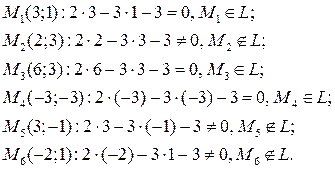
Ответ: точки ![]() и
и
![]() лежат на данной прямой; точки
лежат на данной прямой; точки ![]() и
и ![]() не
лежат на ней.
не
лежат на ней.
Пример 9.
Найти точку пересечения двух прямых ![]()
Решение.
Так как точка ![]() лежит на обеих прямых, то
координаты этой точки должны удовлетворять системе уравнений
лежит на обеих прямых, то
координаты этой точки должны удовлетворять системе уравнений
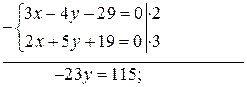
![]()
Ответ: ![]()
Пример 10.
Стороны АВ, ВС и АС
треугольника АВС даны соответственно уравнениями ![]() . Определить координаты его вершин.
. Определить координаты его вершин.
Решение.
Найдем точку В пересечения сторон АВ и ВС треугольника АВС.
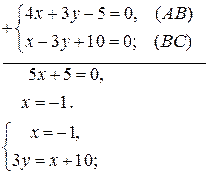
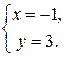
Точка ![]()
Найдем точку А пересечения сторон АВ и АС данного треугольника
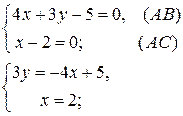
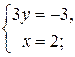
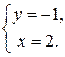
Точка ![]()
Найдем точку С пересечения сторон АС и ВС данного треугольника
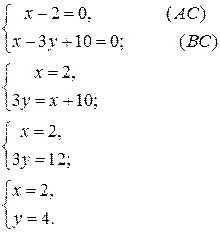
Точка ![]()
Ответ: ![]()
![]()
![]()
Пример 11.
Даны вершины ![]() треугольника АВС. Составить
уравнения медианы, высоты и биссектрисы, проведенных из вершины В.
треугольника АВС. Составить
уравнения медианы, высоты и биссектрисы, проведенных из вершины В.
Решение.
1) Пучок прямых,
проходящих через точку ![]() имеет вид
имеет вид ![]()
2) Найдем
уравнение медианы ![]() . Найдем
координаты середины
. Найдем
координаты середины ![]() отрезка АС
отрезка АС
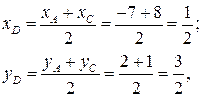
т.е. ![]() Найдем угловой коэффициент
Найдем угловой коэффициент 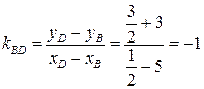 .
.
Подставляя k=-1 в формулу![]() , получаем уравнение медианы BD:
, получаем уравнение медианы BD: ![]() , или
, или![]() .
.
3) Найдем уравнение высоты BE. Найдем угловой
коэффициент AC 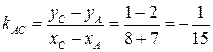 .
.
На основании условий перпендикулярности
двух прямых 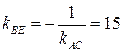 .
.
Следовательно по формуле ![]() уравнение высоты BE примет вид
уравнение высоты BE примет вид
![]() , или
, или ![]()
4) Найдем уравнение биссектрисы BF.
Первый способ. Угловой
коэффициент ![]() получаем из равенства
получаем из равенства ![]() :
:
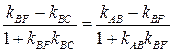
![]() , или
, или ![]()
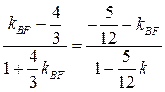 ,
,
(где 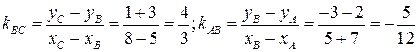 ),
),
Откуда после преобразований имеем ![]() и
и ![]() .
.
Так как биссектриса BF образует тупой
угол с осью Ox то ![]() .
.
Теперь по формуле ![]() уравнение BF примет вид
уравнение BF примет вид
![]() , или
, или ![]() .
.
Второй способ. По формуле![]() найдем уравнения сторон
треугольника AB и BC, учитывая, что
найдем уравнения сторон
треугольника AB и BC, учитывая, что ![]() :
:
![]() , или
, или ![]() (AB);
(AB);
![]() , или
, или ![]() (BC).
(BC).
Учитывая, что по свойству биссектрисы
расстояния ее от любой точки M(x;y) до сторон AB и BC равны, по формуле 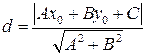
![]() получаем
ее уравнение
получаем
ее уравнение
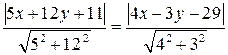
Записанному уравнению удовлетворяют два уравнения:
![]() , или (после
преобразований)
, или (после
преобразований) ![]() и
и ![]() , из которых последнее – уравнение
с отрицательным угловым коэффициентом.
, из которых последнее – уравнение
с отрицательным угловым коэффициентом.
![]() Пример 12.
Пример 12.
Найдите
координаты центра и радиус окружности ![]() .
.
Решение.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Центр окружности – точка (4;5).
Радиус r=7.
Пример 13.
Найдите
вершины, фокусы эксцентриситет и асимптоты гиперболы. ![]()
Решение.
Уравнение
данной гиперболы имеет вид ![]() , т.е.
фокусы ее лежат на оси Оу. Из уравнения получим
, т.е.
фокусы ее лежат на оси Оу. Из уравнения получим ![]() ,
, ![]() и
и
![]() ,
, ![]() .
.
Вершины гиперболы находятся в точках А1(0;8) и А2(0;8).
![]() ,
,
![]() ; следовательно, фокусами служат точки F1(0;-10) и F2(0;10).
; следовательно, фокусами служат точки F1(0;-10) и F2(0;10).
Эксцентриситет
вычислим по формуле ![]() ;
;
![]() .
.
Асимптоты
гиперболы найдём по формуле ![]() .
.
![]() .
.
Пример 14.
Построить
параболу ![]() .
.
Решение.
![]()
![]()
Найдем
вершину параболы, преобразовав уравнение ![]() к виду
к виду
![]()
![]()
![]() ,
,
![]()
![]()
Откуда a=1, b=-9
А(1;-9)
Найдем точки пересечения параболы с осями Ох и Оу.
С осью Ох:
![]()
![]()
![]()
![]()
Точки пересечения с осью Ох: (-2;0), (4;0).
С осью Оу: (0;-8).
Вопросы для закрепления теоретического материала к практическому занятию:
1. Назовите общий вид уравнения прямой?
2. Назовите уравнение прямой с угловым коэффициентом?
3. Назовите каноническое уравнение прямой?
4. Назовите уравнение прямой, проходящей через данную точку?
3. Что называется окружностью?
4. Что называется гиперболой?
5. Что называется параболой?
Содержание отчета:
Название практической работы.
Учебная цель.
Решение заданий практической работы.
Ответы на вопросы для закрепления теоретического материала.
Литература:
1. Григорьев В.П. Элементы высшей математики. –М.: ОИЦ «Академия», 2016.
2. Григорьев В.П. Сборник задач по высшей математике: Учеб. пособие для студентов учрежд. СПО / В.П.Григорьев, Т.Н.Сабурова. – М.: Издательский центр «Академия», 2017. – 160 с.
3. Григорьев Г.В Математика. М.ИЦ Академия, 2017 г.
4. Богомолов Н.В. Практические занятия по математике, учебное пособие для СПО. М.: «Высшая школа», 2016.
5. Богомолов Н. В., Самойленко П.И. Математика. Учебник для ссузов. М.«ДРОФА», 2017.
6. Пехлецкий И. Д. Математика: учебник для студентов образовательных учреждений специального профессионального образования – 3-е издание. – М.: Издательский центр «Академия», 2016.
9. Бардушкин В.В., Прокофьев А.А. Математика. Элементы высшей математики: учебник: в 2 т. Т. 2 / В.В., А.А.— М.: КУРС, НИЦ ИНФРА-М, 2018. — 368 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/
10. Шабунин М.И. Математика: Пособие /- 7-е изд., (эл.) - М.:Лаборатория знаний, 2016. - 747 с.: ISBN 978-5-93208-204-1 - Режим доступа: http://znanium.com/
11. Филипова Е.Е Математика: Учебное пособие /. - Вологда:ВИПЭ ФСИН России, 2015. - 378 с.: ISBN 978-5-94991-312-3 - Режим доступа: http://znanium.com/
12. Балдин, К.В. Математический анализ : учебник / К.В. Балдин, В.Н. Башлыков, Л.В. Рукосуев ; под общ. ред. К.В. Балдина. - 3-е изд., стер. - Москва : ФЛИНТА, 2015. - 361 с. - ISBN 978-5-9765-2067-7. - Режим доступа: http://znanium.com/
Критерии оценки за выполнение практического занятия
|
Оценка |
Критерии |
|
«Отлично» |
Показал полное знание технологии выполнения задания. Продемонстрировал умение применять теоретические знания/правила выполнения/технологию при выполнении задания. Уверенно выполнил действия согласно условию задания. |
|
«Хорошо» |
Задание в целом выполнил, но допустил неточности. Показал знание технологии/алгоритма выполнения задания, но недостаточно уверенно применил их на практике. Выполнил норматив на положительную оценку. |
|
«Удовлетворительно» |
Показал знание общих положений, задание выполнил с ошибками. Задание выполнил на положительную оценку, но превысил время, отведенное на выполнение задания. |
|
«Неудовлетворительно» |
Не выполнил задание. Не продемонстрировал умения самостоятельного выполнения задания. Не знает технологию/алгоритм выполнения задания. Не выполнил норматив на положительную оценку. |
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.