Пояснительная записка

 

При изучении различных учебных дисциплин ученики школы получают всесторонние знания о природе и обществе, но необходима интеграция этих знаний, нужно формировать синтезирующее мышление школьника способного осуществлять межпредметные связи при изучении основ наук.

Математика и физика находятся в неразрывной связи друг с другом. Математика дает физике средства и приемы общего и точного выражения зависимости между физическими величинами, которые открываются в результате эксперимента. Поэтому содержание и методы физики зависят от уровня математической подготовки учащихся.

         При решении задач включенных в данный сборник  рассматривается применение производной, интегралов, дифференциальных уравнений, элементов векторной алгебры, логарифмических и тригонометрических функций     Сборник содержит задачи и готовые решения к ним. Каждой группе задач предшествует краткий теоретический материал и приводится подробное решение задач разного уровня сложности

Пособие предназначено для учащихся 10-11 классов общеобразовательных школ с естественно-математическим направлением, а также для абитуриентов занимающихся подготовкой поступления в ВУЗ.

 

 
1 Раздел      Элементы векторной алгебры

 

         Различают величины векторные и скалярные. Скалярная величина может быть охарактеризована одним числом, выражающим отношение этой величины к соответствующей единице измерения. Примеры скалярных величин: длина, площадь,  объем, температура, сопротивление, электроемкость и т.д. Векторная величина характеризуется числом и направлением. Примеры векторных величин: сила, скорость, ускорение, напряженность электрического поля и т.д.

        Вектор характеризуется следующими элементами: начальной точкой, направлением, длиной. Обозначается вектор МК или  а, а длина вектора   МК  или  а  . Единичным вектором называется вектор, длина которого равна единице. Векторы, лежащие на параллельных прямых называются коллинеарными.  Суммой двух векторов  а  и   в         называется       третий         вектор   с,

              в                         определяемый по правилу параллелограмма. Сумма двух

                                  векторов обладает свойством      переместительности  и

                                  сочетательности .

а                                  а  +  в   =   в  +  а

                                     а  +  в  )   +  с  =  а  +  (  в  +  с  )

 

               а                        Разностью двух векторов а  и  в  называется    такой

                                        вектор   d   который     при     сложении   с     вектором                 

                                         в   дает   вектор  а .

   в                   d              Произведением  вектора    а   на число n называется

                                         новый вектор    na ,  длина   которого  в  n  раз

                                        больше длины    а   и направление а                              совпадает с направление вектора   а ( если n>0) и противоположна                                                                                           (если n < 0).

            2а                                    n ( a + b) =  na  +  nb

                                                    (-n)a  =  - ( na)   

           -2а                                    na  = 0  , если n = 0  

 

Скалярным произведением   двух  векторов  называется     число, равное произведению   их    длин на косинус угла между ними.

                                           а  в   =   а    в  cos  ( ав )

 

 

Примеры решения задач.

 

Задача №1

Найдите скалярное произведение двух векторов а и в, для которых     а    =  8,    в   =   5, в каждом  из следующих случаев:   = 60⁰,      = 120⁰

 

Решение:

Воспользуемся формулой  скалярного произведения векторов 

1. ав = а * в  cos    = 8*5*cos 60⁰  = 20

2. ab = a *b  cos      = 8*5*cos 120⁰  = -20

 

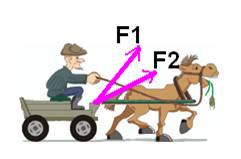Задача №2

На тело действуют две силы  F = 3 H.   F = 4 H составляющие с осью ОХ углы 10 и 40 соответственно.Вычислите равнодействующую сил действующих на тело.

 

Решение:

Векторная сумма сил запишется:                                          

F  =  + , где F – равнодействующая

F – направлена по диагонали параллелограмма                              

построенного на векторах  и , как на сторонах,                                   

численное значение F находим по теореме косинусов.

                                                               

                  

  Ответ: 6,8 Н                                                                                                                                                            

 

Задача № 3

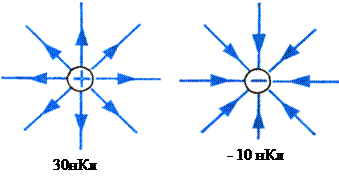Электрическое поле  создано двумя точечными зарядами 30нКл и –10 нКл. Расстояние между ними 20 см. Определить напряженность электрического поля в точке, находящейся на расстоянии 15 см от первого и на расстоянии 10 см от второго зарядов.

Решение:

 

По принципу суперпозиций напряженность электрического поля будет равна векторной сумме напряженностей создаваемых каждым зарядом.

Напряженность создаваемая зарядом равна

Абсолютное значение вектора напряженности найдем по теореме косинусов:

Е=, где угол  - найдем из треугольника со сторонами /

                                             

Подставляя найденные величины, получим итоговую формулу:

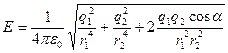
Сделаем вычисления:      Е= 16,7 кВ/м

 

ОТВЕТ:16,7 кВ/м

 

 

 

 

 

                                                                                      Е

                                                      

                                                                       

 

               +                         d                                      

 

 

 

 

Задача № 4

Складываются два колебания одинакового направления, выражаемых уравнениями

, где 

Определить начальные фазы  колебаний, найти амплитуду А  результирующего колебания.

 

Решение.

Уравнение гармонического колебания имеет вид:

   

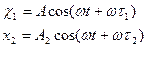
Для определения амплитуды результирующего колебания удобно воспользоваться векторной диаграммой и по теореме косинусов, получим:

учитывая что , А= 2,65 см

                               Ответ: 2,65 см

 

               У                 А                  

              А

 

                               

                                            

                                                                                 Х

 

2 раздел

Производная и ее применение

           Часто в задачах нужно вычислить не значение какой-либо величины, а ее изменение, например, работа – это изменение энергии, скорость – это отношение перемещения к промежутку времени в течение которого это перемещение произошло. Быстрота протекания физических процессов выражается с помощью производной.

         Производной функции Y = f ( x )  в точке х называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

          

Геометрическое значение производной. Производная функции   Y = f ( x ) для каждого значения х равна угловому коэффициенту касательной к графику данной функции в соответствующей точке.

               ,

где - угол, образуемый касательной к  графику с положительным направлением оси ОХ, этот угол является функцией аргумента Х Рассмотрим график функции  y = f ( x ):

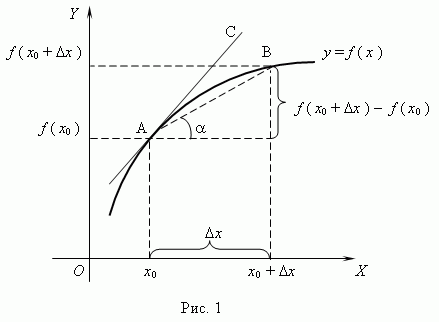
Из рис.1  видно, что для любых двух точек A и B графика функции:  

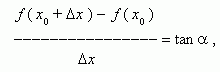
где  - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то  неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x₀ ,  f ( x₀  ) ). В общем случае уравнение прямой с угловым коэффициентом  f ’( x₀ )  имеет вид:

y = f ’( x₀ ) · x + b .

Чтобы найти b, воспользуемся тем, что касательная проходит через точку A:

f ( x₀ ) = f ’( x₀ ) · x₀ + b ,

отсюда,  b =  f ( x₀ ) – f ’( x₀ ) · x₀ , и подставляя это выражение вместо  b, мы получим  уравнение касательной:

y =  f ( x₀ ) +  f ’( x₀ ) · ( x – x₀  ) .

Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан:  координата  x  движущейся точки – известная функция  x ( t ) времени  t. В течение интервала времени от  t₀  до  t₀ +   точка перемещается на расстояние:  x ( t₀ + ) - x ( t₀ ) = , а её средняя скорость равна:  v_a = / . При  0  значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью  v ( t₀ )  материальной точки в момент времени  t₀ . Но по определению производной мы имеем:

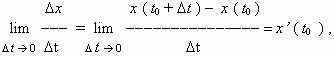
отсюда,  v ( t₀ ) = x’ ( t₀ ) , т.e. скорость – это производная координаты по времени. В этом и состоит  механический смысл производной. Аналогично, ускорение – это производная скорости по времени:  a = v’ ( t ).

 

Механическое значение производной.   Для функции S = F ( t ) меняющейся со временем, производная     есть скорость изменения функции в данный момент времени.

 Основные правила дифференцирования

 

 

 

 

 

 

 

 

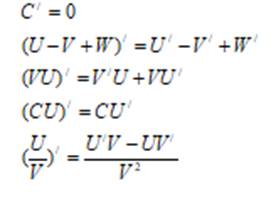
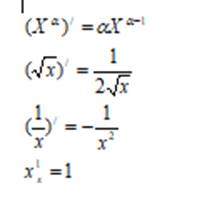
Примеры решения задач:

Задача № 1

Найти производную функции

Решение:

На основании формул производных степенных функций получаем:

 

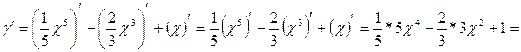
Задача  № 2

 

Нагреватель кипятильника состоит из четырех одинаковых элементов. Сопротивление каждого из них 1 Ом. Нагреватель питается от батареи с ЭДС 8В и внутренним сопротивлением 1 Ом. Элементы нагревателя включены так, чтобы вода нагревалась наиболее быстро. Найти  мощность, расходуемую батареей.

 

Решение:

 

Р max - мощность должна быть максимальной, т.к. t = t min:

P max = .

Мощность зависит от  внешнего сопротивления, выразим эту зависимость математически

                                                P = IR                    

                                              I = P =  = P(R)

Для нахождения максимальной мощности, необходимо исследовать функцию

P(R) = (*)

 

 

1)Найдем промежуток изменения аргумента: R.

 

2)Вычислим производную:

P(R) =  = =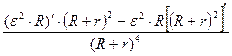

 

===

 

3) Найдем критические точки:

           (R) = 0

            r – R = 0, R = r

 

4) Докажем, что в точке R=r функция  (*) достигает  своего наибольшего значения:

Rr , r-R0       

                    Функция (R)0, R r , r-R0,  функция  (R)0.        

(R + r) 

 

Тогда сопротивление цепи:

R=+=R= r.

R==R= r.

 

Максимальная мощность:

P max = = = = 16

= = ==

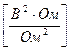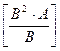Ответ:  P max= 16Вт

 

Задача № 3

 

Лыжник спускается с горы, он  движется по закону .Вычислите скорость, ускорение тела через 2 секунды после начала движения. Запишите уравнение движения скорости и ускорения тела.. Вычислите через какое время тело остановится.

 

Решение.

Зная, что скорость тела это первая производная перемещения, запишем уравнение скорости.

Это и есть уравнение скорости тела. Подставим значение времени.

Зная, что ускорение это первая производная скорости, запишем уравнением/

Подставим в данное уравнение значение времени:

м/

Ответ: 32 м/с²

 

Задача  № 4

 

Парусник должен в кратчайший срок перевозить груз на расстояние 1 км. Он может ускорять или замедлять свой ход только с одинаковым ускорением 0,9 м/с, переходя затем в равномерное движение или останавливаясь. Какую наибольшую скорость должен  развивать парусник, чтобы выполнить указанное требование?

                                                                      

Решение: 

 

 Из рисунка видно, что   S =SS+S = 2S+S 

 t = t+t+t= 2t+t

S= S; t = t, т. к. v= v = 0; v = const

В данной  задаче возможно несколько вариантов решения: время движения тележки будет минимальным в зависимости от первого промежутка времени t, или от первого участка пути S

Можно составить уравнения  t(t) и t(S).

1) Рассмотрим первый вариант:

(1)

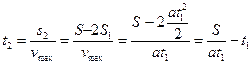Из уравнений кинематики с учетом того, что v имеем  (2)

Подставляем (2) в (1):

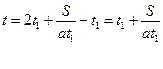
Исследуем функцию на экстремум. Для этого:

 

1. Определим промежуток  изменения аргумента: ;

2. Вычислим производную:

 

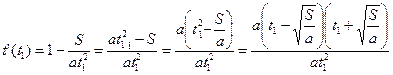
3. Найдем критические точки:

t

t

4. Исследуем знак производной и поведение  функции:

Таким образом, в точке   функция (*) достигает своего наименьшего значения. Значит:

 

Вычисляем максимальную скорость:

Ответ:

 

Задача № 5

 

 Зависимость угла поворота радиуса вращающегося колеса от времени дана уравнением   найти в конце первой секунды вращения угловую скорость колеса, а также полное ускорение точки, лежащей на ободе колеса, если его радиус 2см.

 

 

 

Решение:

 

 Согласно определению угловая скорость колеса , есть первая производная от перемещения 

 

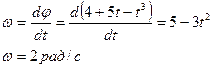
Вычислим угловое ускорение:

 

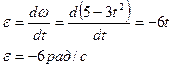
Тогда полное ускорение:

 

 ;

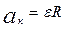Ответ:   м/

 

Задача № 6

 

Уравнение движения лодки дано в виде  Определить начальную скорость и ускорение движения лодки  через 5 мин  после начала движения

 

Решение:

 

Данную задачу можно решить двумя способами:

 

1 способ: Сравним данное уравнение двумя с уравнением движения в общем виде.

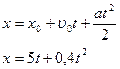                (1)

Очевидно, что х=0, коэффициент при t b t равны

 а=0,8м/с.

Координату тела через 5с найдем из уравнения (1)

Скорость тела через 5с определяется по формуле

 

2 способ: Координату х при t=5c найдем из уравнения (1). По определению скорости

 

 

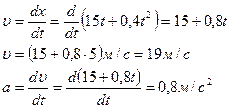
3 раздел

 

Определенный интеграл и его применение

 

Главной задачей механики является умение вычислить координату тела, но для того чтобы ее решить, нужно вычислить перемещение. Проще всего это сделать через площадь криволинейной  трапеции. Для вычисления площади криволинейной трапеции применяется следующая теорема:

Если f – непрерывная и неотрицательная на отрезке  функция, а F – ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке

                       S =  F (b)  –  F  (a)

С другой стороны, площадь криволинейной трапеции может быть вычислена через определенный интеграл.                                                                        

Теорема Ньютона-Лейбница: Определенный интеграл от непрерывной функции в данном промежутке равен разности значений любой первообразной функции для верхнего и нижнего пределов интегрирования: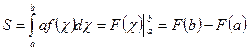        

Эта формула верна для любой функции f, непрерывной на  отрезке , поэтому интеграл можно применять для вычисления других физических величин, например: работы, объема, давления и т.д.

Правила вычисления интегралов:

·        Интеграл суммы равен сумме интегралов

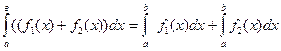
·        Постоянный множитель можно вынести за знак интеграла

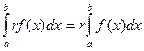
·        Если , то

·        Интегрирование по частям в определенном интеграле:

     

 

Примеры решения задач

 

Задача № 1

Определите площадь, ограниченную параболой  и координатными осями.

Решение:

Найдем пределы интегрирования. Так как фигура ограничена осью OY, то нижний предел интегрирования  а=0.  Кривая   пересекает ось ОХ в двух точках: ,, следовательно, верхний предел b=2. Таким образом,

 

 

 

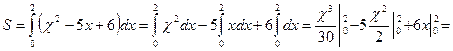
   Y

 

  6

 

            2              3                X

 

Задача № 2

 

Тело движется по закону:. Вычислите пройденный путь за промежуток  времени с первой по седьмую минуты после начала движения.

 

Решение:

Зная, что перемещение тела при неравномерном движении численно равно площади криволинейной трапеции, вычислим ее . Для определения пределов интегрирования найдем точки пересечения кривой с осью  ot. Для этого решая квадратное уравнение, найдем его корни.

 

      , 

Вычислим интеграл:

=()

 

 

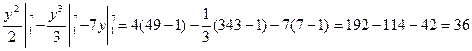   Y    

       7 

 

       1

 

                                                          X

Задача № 3

 

Найти изменение энтропии при нагревании воды массой 100 г от  до  и последующим превращением  воды в пар той же температуры.

 

Решение.

 

Найдем отдельно изменение энтропии при нагревании воды  и изменение энтропии при  превращении ее в пар .Полное изменение энтропии выразится суммой этих энтропий.

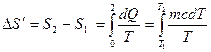
Вынесем за знак интеграла постоянные величины и произведем интегрирование, тогда получим

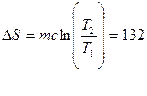Дж/К

При вычислении изменении   энтропии во время превращения воды в пар той же температуры постоянная температура выносится за знак интеграла.

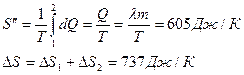
Ответ: 737 Дж/К

 

Задача № 4

 

В некотором объеме газа содержится число молекул, равное постоянной Авогадро N. Рассматривая этот газ как идеальный, определите число молекул N, скорости v которых меньше 0,001 наиболее вероятной скорости v

 

Решение.

 

Для решения задачи удобно воспользоваться распределением молекул по относительным скоростям u (u=). Число dN (u) молекул, относительные скорости u которых заключены в пределах от u до u+du , определяется формулой

 dN(u)= ,                      (1)

 где N– полное число молекул в рассматриваемом объеме.

 По условию задачи, максимальная скорость интересующих нас молекул v=0,001v , откуда u =0,001. Для таких значений u  выражение (1) можно существенно упростить. В самом деле, для u <<1 имеем . Пренебрегая значением u=(0,001)=10 по сравнению с единицей, выражение (1) запишем в виде

       dN(u)=                                                     (2)

Интегрируя это выражение по u  в пределах от 0 до u , получим

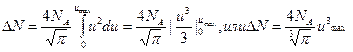
Подставив в последнюю формулу значения величинN,  и u и произведя вычисления, найдем

 Ответ:      молекул.

 

Задача № 5

 

Зная функцию f(p) распределения молекул по импульсам, определить среднее значение квадрата импульса <>.

 

Решение.

 

Среднее значение квадрата импульса <> можно определить по общему правилу вычисления среднего:

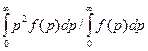<>=                 (1)

Функция распределения молекул по импульсам имеет вид

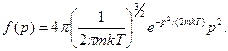              (2)

Эта функция распределения уже нормирована на единицу, т.е.

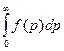  =1. С учетом нормировки формулу (1) перепишем иначе:

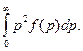
  <>=                               (3) 

Подставив выражение  по уравнению (2) в формулу (3) и вынесем величины, не зависящие от , за знак интеграла:

<>=

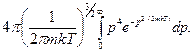
Этот интеграл можно свести к табличному 

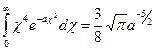   , положив    

В нашем случае этот даст

<>=

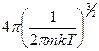
После упрощений и сокращений найдем

<>=

 

Задача № 6

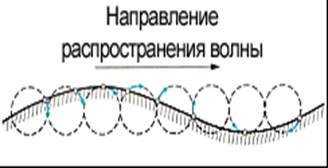
Поперечная волна распространяется вдоль упругого шнура со скоростью

Период  колебаний точек шнура равен 1,2с, амплитуда =2м. определить :1) длину волны   ;2) фазу  колебаний, смещение , скорость   и ускорение   точки, отстоящей на расстоянии =45м о источника волн в момент  =4с ;

3) разность фаз  колебаний двух точек,

 лежащих на луче и отстоящих от источника волн на расстояниях =20м и =30м.

 

Решение.

 

Длина волны равна расстоянию, которое волна проходит за один период, и может быть найдена из соотношения

подставив значения величин и , получим

             =18м.

Запишем уравнение волны:

           (1)

где  - смещение колеблющейся точки;  – расстояние точки от источника волн;  - скорость распространения волн.

Фаза колебаний точки с координатой   в момент времени  определяется выражением, стоящим в уравнении волны под знаком косинуса:

= или

где учтено, что .

произведя вычисления по последней формуле, получим

                =5,24 рад, или  =300.

 смещение точки определим, подставив в уравнение(1) значения амплитуды  и фазы:

=1 см.

скорость  точки находим, взяв первую производную от смещения по времени:

=

Подставив значения величин   и  и произведя вычисления, получим

=9  см/с.

Ускорение есть первая производная от скорости по времени, поэтому

Произведя вычисления по этой формуле, найдем

=27,4 см/ с

Разность фаз  колебаний двух точек волны связана с расстоянием  между этими точками соотношением

Подставив значения величин  , и вычислив, получим

Ответ: =3,49 рад, или =200

 

 

Задача №7

 

Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной .Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (), будет обнаружен в средней трети ящика.

 

Решение.

 

 Вероятность  обнаружить частицу в интервале определяется равенством

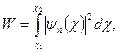    (1)

где   – нормированная собственная волновая функция, отвечающая данному состоянию.

Нормированная собственная волновая функция, описывающая состояние электрона в потенциальном ящике, имеет вид

=

Возбужденному состоянию () отвечает собственная функция

=                             (2)

Подставив  в подынтегральное выражение формулы (1) и вынося постоянные величины за знак интеграла, получим

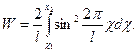
Согласно условию задачи,    и . Подставим эти пределы интегрирования в формулу (3), произведем замену =  и разобьем интеграл на два:

==

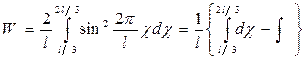Заметив, что а , получим

 Ответ:                            W=0,195.

 

 

Задача № 8

 

Углекислый газ массой 10г нагрет от 20 до 30 С при постоянном давлении. Найти работу расширения газа и изменение внутренней энергии.

 

Решение

 Изменение внутренней энергии углекислого газа при его нагревании от температуры

до температуры  найдем  по формуле

= 0,83=(303-293)Дж=83Дж.

Работа расширения углекислого газа

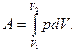                                           (1)

По условию задачи, давление углекислого газа p=const, тогда давление, как постоянную величину, можно вынести из-под знака интеграла и выражение (1) примет вид

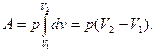                        (2)

Из уравнения  Клапейрона-Менделеева

Находим объем углекислого газа при температуре T:Следовательно, при температурах T и T углекислый газ будет занимать объемы

 и                          (3)

Подставим выражения (3) в (1):

 

Ответ:  А=

 

Задача № 9

 

Кислород массой 6г при температуре 30 расширяется при постоянном давлении, увеличивая свой объем в два раза вследствие притока теплоты извне. Найти работу расширения, изменение внутренней энергии газа и количества теплоты, сообщенное кислороду.

 

Решение.

 

 Изменение внутренней энергии кислорода при его нагревании на   находим по формуле

                                       (1)

Поскольку  расширение кислорода происходит при постоянном давлении p, то, используя закон Гей-Люссака

,

находим конечную температуру кислорода:

.                                (2)

Подставляя выражение (2) в (1), получаем

;

 

Найдем работу расширения:

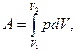
или, учитывая, что p = const,

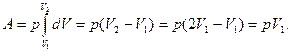           (3)

Из уравнения Клапейрона-Менделеева  найдем объем кислорода при температуре T:

                                                                              (4)

Подставим выражение (4) в (3):

Количество теплоты, сообщенное газу, найдем по первому началу термодинамики

Ответ: 21,44 кДж

 

Задача № 10

 

Какой заряд пройдет через поперечное сечение проводника за промежуток времени от 5 до 10 с от момента включения тока, если сила тока изменяется со временем по закону I=6+3t.

 

Решение:

Заряд может быть вычислен: q=

q===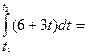  

 

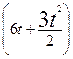
Сделаем вычисления: q = 142,5 Кл.

 

 

Задача № 11

 

Тело вращается так, что зависимость углов скорости от времени дается уравнением .Найти полное число оборотов, совершенных телом за 20с после начала обращения.

 

Решение:

По определению 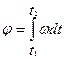  тогда:

       

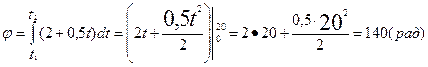
Тогда полное число оборотов тела     N=

Ответ: 22 оборота

 

Задача № 12

Скорость тела выражается формулой найти перемещение тела через 20с от начала движения.

 

Решение:

По определению S=     тогда:

  S=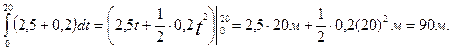     

Ответ: 90 м

 

4 раздел

 

Дифференциальные уравнения и их применение

      Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. (Темп изменения расстояния со временем определяется скоростью; следовательно, скорость – производная от расстояния; аналогично, ускорение – производная от скорости, так как ускорение задает темп изменения скорости со временем.) Большое значение, которое имеют дифференциальные уравнения для математики и особенно для ее приложений, объясняются тем, что к решению таких уравнений сводится исследование многих физических и технических задач. Дифференциальные уравнения играют существенную роль и в других науках, таких, как биология, экономика и электротехника; в действительности, они возникают везде, где есть необходимость количественного (числового) описания явлений (коль скоро окружающий мир изменяется во времени, а условия изменяются от одного места к другому).

Примеры. Следующие примеры позволяют лучше понять, как различные задачи формулируются на языке дифференциальных уравнений.

1) Закон распада некоторых радиоактивных веществ состоит в том, что скорость распада пропорциональна наличному количеству этого вещества. Если x – количество вещества в некоторый момент времени t, то этот закон можно записать так:

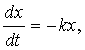
где dx/dt – скорость распада, а k – некоторая положительная постоянная, характеризующая данное вещество. (Знак «минус» в правой части указывает на то, что x убывает со временем; знак «плюс», подразумеваемый всегда, когда знак явно не указан, означал бы, что x возрастает со временем.)

2) Емкость первоначально содержит 10 кг соли, растворенной в 100 м³ воды. Если чистая вода вливается в емкость со скоростью 1 м³ в минуту и равномерно перемешивается с раствором, а образовавшийся раствор вытекает из емкости с такой же скоростью, то сколько соли окажется в емкости в любой последующий момент времени? Если x – количество соли (в кг) в емкости в момент времени t, то в любой момент времени t в 1 м³ раствора в емкости содержится x/100 кг соли; поэтому количество соли убывает со скоростью x/100 кг/мин, или

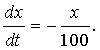
3) Пусть на тело массы m, подвешенное к концу пружины, действует возвращающая сила, пропорциональная величине растяжения пружины. Пусть x – величина отклонения тела от положения равновесия. Тогда по второму закону Ньютона, который утверждает, что ускорение (вторая производная от x по времени, обозначаемая d ²x/dt ²) пропорционально силе:

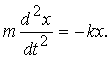
Правая часть стоит со знаком минус потому, что возвращающая сила уменьшает растяжение пружины.

4) Закон охлаждения тел утверждает, что количество тепла в теле убывает пропорционально разности температур тела и окружающей среды. Если чашка кофе, разогретого до температуры 90° С находится в помещении, температура в котором равна 20° С, то

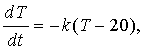
где T – температура кофе в момент времени t.

5) Министр иностранных дел государства Блефуску утверждает, что принятая Лиллипутией программа вооружений вынуждает его страну увеличить военные расходы на сколько это только возможно. С аналогичными заявлениями выступает и министр иностранных дел Лиллипутии. Возникающую в результате ситуацию (в простейшей интерпретации) можно точно описать двумя дифференциальными уравнениями. Пусть x и y – расходы на вооружение Лиллипутии и Блефуску. Предполагая, что Лиллипутия увеличивает свои расходы на вооружение со скоростью, пропорциональной скорости увеличения расходов на вооружение Блефуску, и наоборот, получаем:

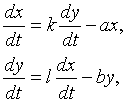
где члены -ax и -by описывают военные расходы каждой из стран, k и l – положительные постоянные. (Эту задачу впервые таким образом сформулировал в 1939 Л.Ричардсон.)

После того, как задача записана на языке дифференциальных уравнений, следует попытаться их решить, т.е. найти величины, скорости изменения которых входят в уравнения. Иногда решения находятся в виде явных формул, но чаще их удается представить лишь в приближенном виде или же получить о них качественную информацию. Часто бывает трудно установить, существует ли решение вообще, не говоря уже о том, чтобы найти его. Важный раздел теории дифференциальных уравнений составляют так называемые «теоремы существования», в которых доказывается наличие решения у того или иного типа дифференциальных уравнений.

Первоначальная математическая формулировка физической задачи обычно содержит упрощающие предположения; критерием их разумности может служить степень согласованности математического решения с имеющимися наблюдениями.

Примеры решения задач:

 

Задача № 1

 

Показать, что функция является решением дифференциального уравнения

 

Решение:

 

Найдем производную данной функции:  ,  ,  .

Подставляя выражения и у  в дифференциальное уравнение, получим:

Это решение является частным ,потому что не содержит произвольных постоянных.

 

Задача № 2

 

Моторная лодка движется в спокойной воде со скоростью 5 м/с. На полном ходу ее мотор выключается и через 40 с после этого, скорость лодки уменьшилась до 2 м/с. Определите скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

 

Решение:

На лодку действует сила сопротивления воды:     , где k – коэффициент пропорциональности. Составим систему уравнений:

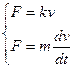
Учитывая,  что левые части уравнений равны, приравняем правые чвсти:

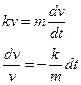
Проинтегрируем это уравнение и найдем общее решение:

, учитывая ,что скорость равна 5 м/с при t=0

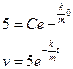
если t= 40 c. V=2 м/с,

     ,      

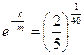
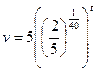
при t= 2 мин = 120 с

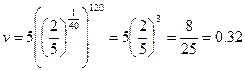 м/с

Ответ: 0,32 м/с

 

ЗАДАЧА №3

 

Автобус  движется по прямой линии с постоянным ускорением 2 .Найти закон движения мяча и вычислить  его перемещение через 12 с после начала движения.

 

Решение:

 

В качестве независимой переменной выберем время, тогда пройденный путь и скорость точки будут функциями времени. Так как ускорение точки при прямолинейном движении равно производной скорости по времени, то по условию задачи можно составить следующее дифференциальное уравнение первого порядка с разделяющимися переменными:

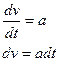
Интегрируя уравнение, получаем  . Значения С определяем из начальных условий:  при t=0.

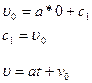
Подставляя  в формулу выражение для скорости через производную от пути по времени

 получим новое диф. уравнение первого порядка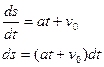

Интегрируя это уравнение, найдем общее решение задачи:

Сделаем вычисления: s=168 м

 

 

Задача  №4

 

Определите форму зеркала, отражающего лучи точечного источника параллельным пучком,

 

Решение:

 

Источник свете примем за начала координат, а ось ох направим параллельно отраженным лучам.

Пусть М(х,у) – произвольная точка кривой, являющаяся сечением зеркала плоскостью Оху. Проведем нормаль к кривой в точке М до пересечения с осью Ох в точке К(х,0). Обозначим   Согласно закону отражения

 

Так как ,  то  - равнобедренный, причем ОМ=ОК

ОМ=

Отрезок ОК определим из уравнения нормали:

  М                                              Е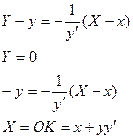                                          

              О                 Е                                

                                                   

                          Подставляя в равенство ОМ=ОК получаем                                                                              однородное дифференциальное уравнение:                                                                               =    Дифференцируя второе равенство по х, получим

   

                     

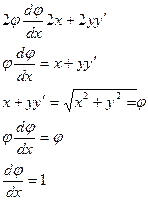
 таким образом,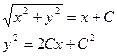

Ответ:  Кривые эти являются параболами. Поверхность искомого зеркала – параболоид вращения.

 

Задача  № 5

 

Лодка движется в спокойной воде со скоростью 2 м/с. На полном ходу мотор выключается и через 30 с после этого скорость лодки уменьшается до 1,5 м/с. Определите скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости лодки.

 

Решение:

 

Примем за независимую переменную время, тогда скорость лодки будет некоторой функцией времени. На движущуюся лодку действует сила , где k- коэффициент пропорциональности. С другой стороны, по закону Ньютона сила равна  

Составим дифференциальное уравнение с разделяющимися переменными:

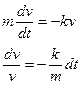
Интегрируя это уравнение находим его общее решение

                      , где С = =2 м/с

Задача № 6

 

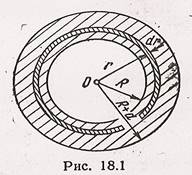
 Металлический шар радиусом R = 3 см  несёт заряд Q = 20 н Кл.

Шар окружен слоем парафина толщиной d = 2 см. Определить энергию W электрического поля, заключённого в слое диэлектрика.

 

Решение.

 

 Так как поле, созданное заряженным шаром, является неоднородным, то энергия поля в слое диэлектрика распределена неравномерно. Однако объемная плотность энергии будет одинакова во всех точках, отстоящих на равных  расстояниях от центра сферы, так как поле заряженного шара обладает сферической симметрией.

         Выразим  энергию в элементарном сферическом поле диэлектрика объемом dV:

         dW = dW,где    - объемная плотность энергии  (рис. 18.1)

Полная энергия выразится интегралом

 

,   (1)

где  r – радиус элементарного  сферического слоя; dr – его толщина. Объемная плотность энергии определяется по формуле , где  E – напряженность поля. В нашем случае  и, следовательно,

                             ,

Подставив это выражение плотности  в формулу (1) и вынеся за знак  интеграла постоянные величины, получим

 

Произведя вычисления по этой формуле, найдем           W=12 мкДж.

Задача № 7

 

 Диполь с электрическим моментом  p = нКл*м находится в однородном  электрическим поле  напряженностью E= 30 . Вектор  p составляет угол  с направлением силовых линий поля. Определить произведенную внешними силами работу А поворота диполя на угол .

 

Решение.

 Из исходного положения (рис.16.2, а) диполь повернуть на угол  = двумя способами: или  по часовой стрелке до угла (рис.16.2,б), или против часовой стрелки до угла (рис. 16.2,в)

В первом случае диполь будет повертываться под действием сил поля. Следовательно, работа  внешних сил при этом отрицательна. Во втором случае поворот  может быть произведен только под действием внешних сил, и, следовательно, работа  внешних сил при этом  положительна.

Работу, совершаемую при повороте диполя, можно вычислить двумя способами:  1) непосредственно интегрированием выражения элементарной работы; 2) с помощью соотношения между работой и изменением потенциальной энергии диполя в электрическом поле.

 

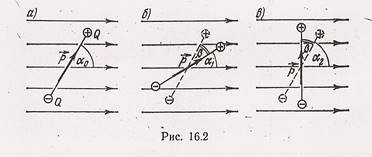
1-й способ. Элементарная работа при повороте диполя на угол

dA=Md

а полная работа при повороте на угол от  до

Произведя интегрирование, получим

().                      (1)

Работа внешних сил  при повороте диполя  по часовой стрелке

мкДж,

против часовой стрелки

мкДж.

 

Задача № 8

 

Электрическое поле создано длинным цилиндром радиусом R=1 см, равномерно заряженным  с линейной плотностью =20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстояниях  a= 0,5 см и а= 2 см от поверхности цилиндра, в средней его части.

 

Решение.

 

Для определения  разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциала , или    

Интегрируя последнее выражение, найдем  разность потенциалов двух точек, отстоящих на r и rот оси цилиндра:

                                                             (1)

Так как цилиндр  длинный и точки взяты  вблизи его средней части,  то для выражения напряженности поля можно воспользоваться формулой . Подставив  это выражение Е в равенство (1), получим

, или

 

.                                                 (2)

Так как величины  и  входят  в формулу в виде отношения, то их можно выразить в  любых, но только одинаковых единицах:

 .

Подставив значения величин , ,  и  в формулу (2) и вычислив, найдем

 

 

Задача № 9

 

 Электрическое поле создано тонким стержнем, несущим равномерно распределенный по длине заряд мкКл/м.  Определить потенциал  поля в точке, удаленной от концов стержня на расстояние, равное длине стержня.

 

Решение

 

Заряд, находящийся на стержне, нельзя считать точечным, поэтому непосредственно применять для вычисления потенциала формулу:

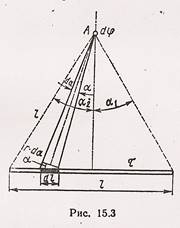
 ,                                        (1)

справедливую только для точечных зарядов, нельзя. Но если разбить стержень на элементарные отрезки dl, то заряд  dl, находящиеся на каждом из них можно рассматривать как точечный и тогда формула (1) будет справедлива. Применив эту формулу, получим

 

       

,                                        (2)

 где   r -  расстояние точки, в которой определяется потенциал, до элемента стержня.

Из рис.15.3 следует, что dl.

подставив это выражение dl  в формулу (2), найдем

.

 

Интегрируя полученное выражение в пределах от до , получим потенциал, создаваемый всем зарядом, распределенным на стержне:

.

В силу симметрии расположения точки А относительно концов стержня имеем  и поэтому

Следовательно, .

Так как      (см. табл. 2), то

.

Подставляя пределы интегрирования, получим

 .

Сделав вычисления по этой формуле, найдем

 

Задача №10

 

 Электрическое поле создано тонкой бесконечно длинной нитью, равнмерно заряженной с линейной плотностью   На расстоянии a = 20 см от нити находится плоская круглая площадка радиусом  r = 1 см. Определить поток  вектора напряженности  через  эту площадку, если   плоскость ее составляет угол  с линией напряженности, проходящей  через середину площадки.

 

Решение.

 

 Поле, создаваемое бесконечно равномерно заряженной нитью, является неоднородным. Поток вектора напряжённости в этом  случае  выражается  интегралом

                                                         

  

где En – проекция вектора  E на нормаль n к поверхности  площадки dS. Интегрирование  выполняется по всей  поверхности площадки, которую пронизывают линии напряжённости.     Проекция  En вектора напряжённости  равна, как видно из рис. 14.6,

 

  En = E cos,

 

где  - угол между направлением вектора и нормалью n.

С учётом этого формула (1) примет вид.

 

 Так как размеры поверхности площадки малы по сравнению  с расстоянием до нити (r <<), то электрическое поле в пределах площадки можно считать практическим однородным. Следовательно, вектор напряженности  Е очень мало меняется по абсолютному значению и направлению в пределах площадки, что позволяет заменить под знаком интеграла значения Е и cos  их средними значениями <E> и <cos> и вынести их за знак интеграла :

.

Выполняя интегрирование и заменяя <E> и <cos> их приближёнными значениями Е и cos, вычисленными для средней точки площадки, получим: .                                                  (3)               

Напряжённость  вычисляется по формуле  . Из рис. 14.6 следует                                                                                                        cos  

С учётом выражения  и cos равенство (3) примет вид:

       или      

 

Поставив в последнюю формулу данные и произведя вычисления, найдём: .

 

Задача № 11

 

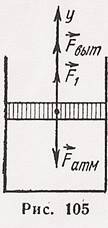В цилиндре под невесомым поршнем площадью 15см находится воздух массой 0,2 г при температуре 20С. Определить работу, которую надо совершить при медленном  равномерном подъеме поршня на высоту от 10 до 20 см. Атмосферное давление нормальное.

 

Решение.

 

 При равномерном подъеме поршня на него действуют: F- внешняя сила, F – сила давления со стороны воздуха, находящегося под поршнем, F - сила давления атмосферного воздуха (рис. 105). Найдём работу внешней силы по подъему поршня на h 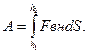                                          (1)

Чтобы найти внешнюю силу, запишем условие равновесия поршня в скалярной форме относительно оси Y:F+ F - F = 0, откуда:Согласно определению,   Здесь - атмосферное давление; p = mRT/(V)- давление воздуха, находящегося под поршнем, где V = Sh – обьём воздуха,  находящегося под поршнем, когда поршень находится на произвольной высоте h. Тогда выражение для силы давления воздуха,

находящегося под поршнем, примет вид F = mRT/(h). Подставляя формулы для  и F в выражение (1) и производя интегрирование, получаем

 

 

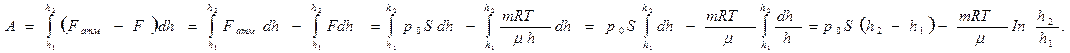
Поскольку движение поршня медленное, то температуру Т можно считать постоянной и вынести при интегрировании за знак интеграла:

 

 

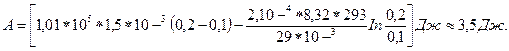
Задача  № 12

 

Атом водорода находится в состоянии 1s. Определить вероятность W пребывания электрона в атоме  внутри сферы радиусом r = 0,1 а (где а – радиус первой боровской орбиты). Волновая функция, описывающая это состояние, считается известной.

 

Решение

Вероятность обнаружить электрон в окрестности точки 0 координатами r,  в обьёме  dV определяется равенством:

В ls – состоянии волновая функция  сферически симметрична, т. е. зависит только от r, и поэтому

                                              (1)

 

где  - собственная нормированная волновая функция, отвечающая основному состоянию:

Благодаря сферической симметрии  - функции вероятность обнаружить электрон на расстоянии r одинакова по всем направлениям. Поэтому элемент объема сферического слоя радиусом r и толщиной

С учётом выражений  и dV формула (1) запишется в виде:

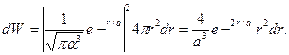
 При вычислении вероятности удобно перейти к атомным единицам, приняв в качестве единицы длины радиус первой боровской орбиты а. Если ввести безразмерную величину p = r/a, то

  и .

Вероятность найдём, интегрируя dW в пределах от  до а (или от до

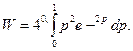
Этот интеграл может быть точно вычислен интегрированием по частям, однако при малых выражение можно разложить в ряд Маклорена:         

и произвести приближённое вычисление.

Пренебрегая всеми членами степени выше первой, запишем интеграл в виде: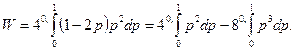

Первый и второй интегралы дают соответственно результаты:

 

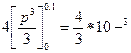и

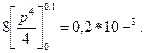
Таким образом искомая вероятность

Знак минус показывает, что в данном случае магнитный момент уменьшился. Подставив значение         

 

Задача №13

Определить заряд Q, прошедший по проводу  сопротивлением R = 3 Ом при равномерном нарастании напряжения на концах провода от UB до U = 4 B в течение t = 20 c.

 

Решение.

Так как сила тока в проводе изменяется, то воспользоваться для подсчёта заряда формулой Q = It нельзя. Поэтому возьмём дифференциал заряда dQ = Idt и проинтегрируем:

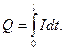                                                                         (1)

Выразив силу тока по закону Ома, получим

                                                                        (2)

Напряжение U в данном случае переменное. В силу равномерности нарастания оно может быть выражено формулой:

                                                                      (3)

где R – коэффициент пропорциональности. Подставив это выражение U в формулу (2) найдём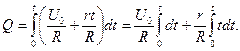                 

Проинтегрировав, получим               (4)

Значение коэффициента пропорциональности r найдём мз формулы (3), если заметим, что при t = 20 C  U = 4 B t

Подставив значения величин в формулу (4), найдём          

 

 

Задача № 15

 

Пылинки массой m= г взвешены в воздухе. Определить толщину слоя воздуха, в пределах которого концентрация пылинок различается не более чем на 1%. Температура т воздуха во всем объеме одинакова и равна 300К.

 

Решение.

 

 При равновесном распределении пылинок концентрация их зависит только от координаты  по оси, направленной вертикально. В этом случае к распределению пылинок можно применить формулу Больцмана

(1)              

Так как в однородном поле силы тяжести U=mgz, то

(2)             

По условию задачи изменение n концентрации с высотой мало по сравнению с n 

( =0,01), поэтому без существенной погрешности изменение концентрации  можно заменить дифференциалом  dn.

  Дифференцируя выражение (2) по  z, получим

Так как  , то

Отсюда находим интересующее нас изменение координаты:

Знак минус показывает, что положительным изменениям координаты (dz>0) соответствует уменьшение относительной концентрации (dn<0). Знак минус опустим (в данном случае он несуществен) и заменим дифференциалы dz и dn конечными приращениями и n

                         

подставим в эту формулу значения величин   =0,01,   Т=300К, m=10 кг, g=9,81м/с, произведя вычисления, найдем

как видно из полученного результата, концентрация даже таких маленьких пылинок (m=  г) очень быстро изменяется с высотой.

 

5раздел

 

Исследование  функции. Экстремумы

 

Решение многих практических задач часто сводится к нахождению наибольшего и наименьшего значения, непрерывной на отрезке функции.

Функция возрастает на множестве Р, если для любых    из множества Р, таких, что

, выполнено неравенство

Функция убывает на множестве Р, если для любых значений , из множества Р, таких, что , выполнено  неравенство

Для точек максимума и минимума функции принято общее название – их называют точками экстремума .  По теореме Ферма, необходимым условием экстремума является:

Если точка    является точкой экстремума функции и в этой точке существует производная то она равна нулю:

Точка будет точкой максимума функции, если в это точке производная меняет знак с плюса на минус.

 Точка  будет точкой минимума, если  в этой точке производная функции меняет знак  с минуса на плюс.

Наибольше и наименьшее значение непрерывной функции могут достигаться как внутри отрезка, так и на концах. Если наибольшего ( наименьшего) значения  функция достигает во внутренней точке отрезка, то эта точка является точкой экстремума.

Алгоритм отыскания наибольшего ( наименьшего ) значения непрерывной функции

                                               на отрезке

 

·        Найти

·        Найти точки, в которых  не существует, и отобрать из них те, что лежат внутри отрезка

·        Вычислить значение функции  в критических  точках  и на концах отрезка и выбрать из них наибольшее и наименьшее ,они и будут соответственно наибольшим и наименьшим значением функции

 

Примеры решения задач

 

Задача № 1

 

Найти наибольшее и наименьшее значение непрерывной функции  на отрезке

 

Решение.

 

Найдем производную:

·          существует при всех Х. Найдем точки, в которых . Имеем:

 

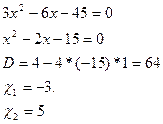
Отрезку принадлежит лишь точка х=5

·        вычислим значения функции в точках 0,5,6.

              

х	0	5	6
у	225	50	63

 

 Наибольшим из найденных значений функции является число 225, наименьшим    –   число 50.         Итак

 

Задача № 2

 

Тело движется по закону . Вычислит наибольшее значение скорости на промежутке сначала движения  по пятую минуты после начала движения.

 

Решение.

 

Найдем производную функции.

Найдем критические точки ()

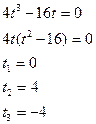
Условию удовлетворяют только точки  

Вычислим значение скорости в этих точках:

T	0	4	5
V	9	119	416

 

Наибольшее значение скорости было на 5 минуте после начала движения.

 

Задача № 3

 

Чему  равно наименьшее расстояние между предметом и его действительным изображением, которое дает собирающая линза  с  фокусным расстоянием 40см?

 

Решение:

 

Обозначим f + d = x (см. рис.)

Рассмотрим зависимость x от расстояния между предметом и собирающей

 линзой, т. е. от d; подставим f = x- d в формулу линзы:

 

= +                                                                                                    

Найдем x(d):     

                         F=

                          X = (*)

Исследуем функцию (*) на экстремум, для этого:

   1.Найдем промежуток изменения аргумента: d.

   2.Вычислим производную:

(d)====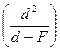

===.

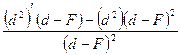d (d-2F)=0.

 

Найдем критические точки: d = 2F.

Исследуем знак производной и поведение функции:

 

Т. о. в точке d =2F функция  (*)  достигает своего максимального  значения .

  Найдем значение x:

== 4F

Вычислим минимальное расстояние между предметом и его действительным изображением:      = 4F =0,4 = 1,6

Задача № 4

 

Велосипед  с колесами радиусом  40см движется

со скоростью 10 по горизонтальной дороге. На какую максимальную высоту может быть заброшена грязь, срывающаяся с колес ?

 

Решение:

 

Предположим, что кусочек земли оторвался от колеса в точке А.Угол между радиусом, проведенным в точку и вертикалью  обозначим.

 

= (1)

  (2)

 

h=

Подставляем формулы(2) и (3) (1):

h=R

1.Исследуем функцию , для этого определим промежуток изменения аргумента:

2.Вычислим производную:

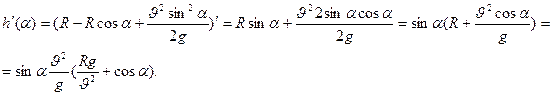
3.Найдем критические точки:

                              

 - не явл. кр. т.

Или

- не явл. кр. т.

4.Исследуем знак производной:

при всех значениях значит, знак зависит от

Вычисляем:

 

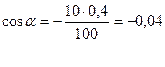
6 Раздел

 

Построение графика функции

Пусть нужно построить график функции . Для этого нужно рассмотреть некоторые свойства функции, что обычно сопровождается соответствующей иллюстрацией на координатной плоскости. Это помогает создать графический образ функции и обратно: графическое представление помогает лучше понять свойства функции, а иногда и предвидеть их.

План построения графика:

1.     найти область определения функции

2.     найти точки ,в которых   f (х)=0  ( это точки пересечения графика с осью абсцисс)

3.     отметить на оси ОХ точки ,найденные в п.2 и точки в которых функция не определена, эти точки разбивают ось ОХ на несколько промежутков, на каждом из которых функция сохраняет свой знак. Установить знак функции на каждом их промежутков.

4.     Исследовать функцию на четность и нечетность

5.     найти вертикальные и горизонтальные асимптоты

6.     исследовать функцию на экстремумы

7.     построить график

Для периодических функций полезно с самого начала найти основной период, и построить ветвь графика на промежутке Затем воспользовавшись периодичность, построить весь график.

 

Примеры решения задач

 

Задача№ 1

Постройте график функции 

 

Решение

 

1.     Функция определена при всех значениях Х

2.     Из уравнения находит точки пересечения с осью ОХ

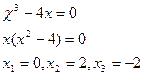
3.     точки –2,0,2 разбивают ось абсцисс на четыре промежутка.

 

 

                   -2                            0                                2     

4.     Исследуем функцию на четность и нечетность:

значит, функция нечетна, ее график симметричен относительно начала координат

5.     асимптот у графика нет

6.    

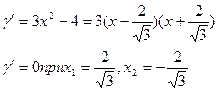
Вычислим значение функции в этих точках:

 

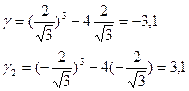
х	()	-2	(-2,0)	0	(0,2)	2	(2,)
		0	+	0		0	+
у		Min Y=-3.1		Y=0		Max Y=3.1

                                      

                                            У

 

 

 

 

 

 

                            2                0            2                           Х

 

 

 

Задача № 2

 

Скорость тела изменяется по закону  . Постройте график скорости и определите максимальное значение скорости за первые з минуты  движения

Решение.

 

1.        Функция определена  при всех значениях t.

 2.       Найдем точки пересечения графика с осью ot:

                                   

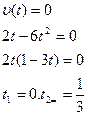
 3.         Найдем точки экстремума: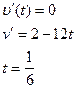                          

 4    Вычислим значение скорости в точке экстремума ( эта точка будет точкой максимального значения скорости)

 (м/с)

v

 

 

   0                                             Х     

 

 

 

 

 

7  раздел

 

Логарифмические  функции

 

При решение задач часто встречается показательная функция вида , где а >0,

Существует обратная ей функция – логарифмическая: , где а>0,

Логарифмическая функция обладает следующими свойствами:

·        область определения  

·        область значения   

·        функция  ни четная, ни  нечетная

·        функция возрастает на промежутке , убывает на  при 0<a<1

Среди показательных функций особый интерес представляет функция обладающая свойством: касательная к графику функции в точке (0,1) образует с осью Х угол . Основание  а такой функции принято обозначать буквой е, т.е. . Подсчитано, что е=2,71828…   Логарифмическую функцию обратную этой показательной функции принято обозначать 

 

Основные свойства логарифмов:

 

 

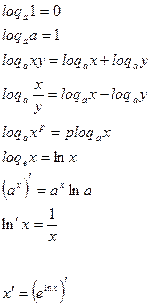
Примеры решения задач

 

Задача № 1

Найдите логарифм числа  по основанию

Решение. Учитывая, что , поэтому по определению логарифма

Задача:

 

Электрон с энергией Е=4,9 эВ движется в положительном направлении оси Х. Высота потенциального барьера равна 5 эВ. При какой ширине барьера вероятность прохождения электрона через него будет равна 0,2.

 

Решение:

 

Вероятность прохождения частицы через потенциальный барьер по своему физическому смыслу совпадает с коэффициентом прозрачности  D. Тогда вероятность того ,чтоэлктрон пройдет через прямоугольный потенциальный барьер, выразится соотношением

 , где m – масса электрона.

Потенцируя это выражение, получим

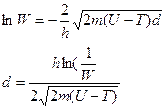
Сделаем вычисления:

D=0,495 нм

 

Задача № 2

 

Определите  период полураспада Ra,  если за 1 сутки из 1 миллиона атомов распадается 175000 атомов.

 

Решение.

 

Период  полураспада определяется по формуле:          (1)

Число распавшихся атомов определим:    ,

 где - число распавшихся атомов

         - число не распавшихся атомов в начальный момент времени

   - число не распавшихся атомов через одни сутки

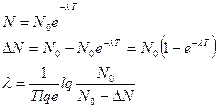  (2)

Подставим  (2) в (1)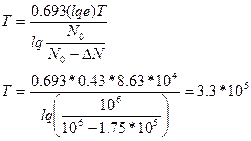     

Ответ: Т= 3,3.*(с)

 

Задача № 3

 

В цилиндре под поршнем находится водород массой 0,02 кг  при температуре 300К. Водород начал расширяться адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце расширении работу, совершенную газом.

 

Решение.

Температура и объем связаны между собой соотношением 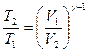     где у=1,4

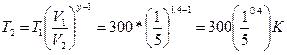
Прологарифмируем части этого выражения:

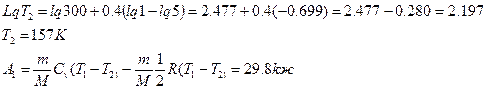
Работа газа при изотермическом сжатии выражается формулой

Знак минус показывает , что при сжатии газа работа совершена внешними силами.

Общая работа в двух процессах:

А=

 

Задача № 4

 

Радиоактивный натрий  распадается, выбрасывая -частицы. Период полураспада 14,8ч. Вычислите количество атомов, распавшихся в 1мг Na за 10ч.

 

Решение:

 

Число распавшихся атомов за время t

  где  - число нераспавшихся

 атомов в начальный момент

- число нераспавшихся атомов через  время  t      

           (2) 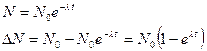   подставим (2) в (1)

Учитывая, что  (3)

 

 

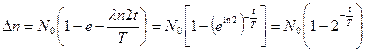
Выражение (3) примет вид

      

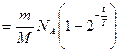
Сделаем  вычисления:   

                  

Скачано с www.znanio.ru