

Рекомендовано к изданию редакционно-издательским советом Лицея 180
Рецензенты:
М.А. Урутина , учитель высшей категории МБОУ СОШ №62 кандидат педагогических наук
Е.В. Корчагин, заслуженный учитель России
Л.А. Новожилова, учитель высшей квалификационной категории МАОУ лицей №180
Тела. Поля. Кинематика и Динамика материальной точки: учеб. Пособие Д.Н. Бибиков. Н.Новгород : МБОУ Лицей 180, 2014. – 116 с.
Данное учебное пособие посвящено разделу физики «Механика».
Учебное пособие содержит изложение теоретических и методологических основ физических явлений на макро- и микроуровне. В нем представлены цели, задачи и основные подходы к решению задач образования на основе Федерального закона Российской
Федерации от 29 декабря 2012 г. N 273-ФЗ "Об образовании в Российской Федерации"
Учебное пособие предназначено для учащихся, обучающихся по программам углублённого изучения физики и математики.
© Бибиков Д.Н.
2015
![]()
Физика – одна из ведущих естественных наук. «Фюзис» с греческого – природа. Всё, что окружает нас, мы называем материей. « Материя » – есть объективная реальность, данная нам через ощущения. Под ощущением мы понимаем не только наши органы чувств, но и различные приборы: телескопы, микроскопы, измерительные приборы и т. д. Материя постоянно изменяется в пространстве и во времени. Свойства пространства и времени зависят от материи. Основные свойства материи – движение и взаимодействие. Движение не только как перемещение, но как любое изменение: нагревание тела, превращение воды в пар и т.д. Взаимодействие в физике, воздействие тел или частиц друг на друга (притяжение или отталкивание), приводящее к изменению состояния их движения и изменению их формы. Для описания этих изменений (явлений) вводят количественные оценки (физические величины): скорость, температура, объем. Физическая величина, свойство, общее в качественном отношении многим физическим объектам (физическим системам, их состояниям и происходящим в них процессам), но в количественном отношении индивидуальное для каждого объекта. К физическим величинам, характеризующим свойства объектов, относятся длина, масса, электрическое сопротивление и т.п., к физическим величинам, характеризующим состояние системы, – давление, температура, магнитная индукция и т.п., к физическим величинам, характеризующим процессы, – скорость, мощность и др. Измерить физическую величину - значит сравнить её с однородной, эталонной величиной, принятой за единицу измерения. Длину стола можно сравнить с единицей длины метром, но не с килограммом! Для всякого измерения недостаточно знания единицы, нужен прибор, который измеряет эту величину. Например, линейка, штангенциркуль, амперметр, вольтметр и т.д.
 Все
единицы физических величин собраны в систему. В настоящее
время пользуются международной системой физических единиц – «СИ». В
любой системе есть основные единицы, принятые по договоренности, и производные,
которые выражаются через закономерности между физическими величинами.
Все
единицы физических величин собраны в систему. В настоящее
время пользуются международной системой физических единиц – «СИ». В
любой системе есть основные единицы, принятые по договоренности, и производные,
которые выражаются через закономерности между физическими величинами.
На современном этапе развития естествознания исследователи различают следующие виды материи: вещество, физическое поле и физический вакуум. Мы будем рассматривать два вида вещество (частицы) и поля (пространства с
определёнными свойствами), хотя на уровне элементарных частиц вещество может иметь свойства поля, а поля – свойства частиц.
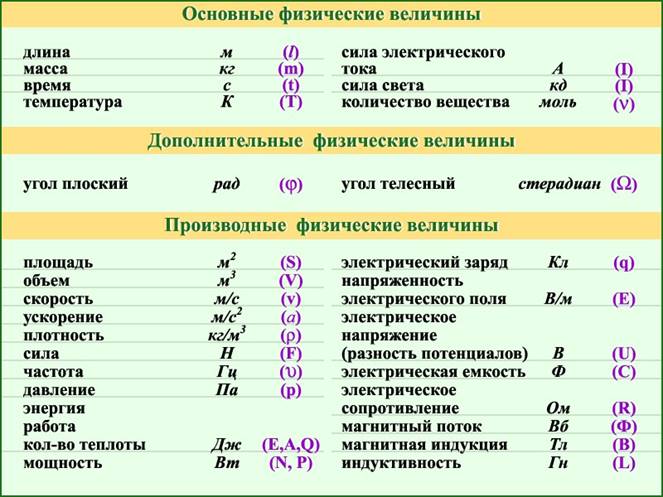
К веществу мы отнесём элементарные частицы, атомы, молекулы, макротела. Поля: гравитационное, электромагнитное, сильное и слабое. Основные единицы можно увеличивать и уменьшать, путем умножения или деления на 10, 100 и т.д. Это обозначается приставками : санти, мили, кило, мега и т.д.
По степени сложности вещество можно расположить следующим образом:
1. Микротела
2. Элементарные частицы.
3. Атомы (состоят из элементарных частиц).
4. Молекулы (состоят из атомов).
5. Макротела (состоят из молекул).
6. Тела, состоящие из множества молекул.
7. Малые космические тела(кометы, астероиды..)
8. Планеты.
9. Звёзды.
10. Звёздные скопления. Галактики. Вселенная.
Мы видим, что в природе существуют связанные системы. Наличие связанных систем говорит о том, что существует взаимное влияние частей системы друг на друга - взаимодействие.
Физические объекты проявляют себя в движении и взаимодействии. Существует четыре вида фундаментальных взаимодействий:
1. Гравитационные взаимодействия (тяготение).
2. Электромагнитные взаимодействия.
3. Сильные (ядерные) взаимодействия.
4. Слабые взаимодействия.
Взаимодействия передаются особым видом материи - полями, поэтому у них соответствующие названия. Но поля это самостоятельный вид материи и они могут существовать отдельно от вещества.
Основными величинами, характеризующими взаимодействие и движение, являются: сила, импульс, энергия. Между физическими величинами существуют устойчивые
связи, которые записываются в виде математических уравнений и называются
U
физическими законами: закон Архимеда F=ρgV, закон Ома I ![]() .
.
R
Все законы можно разделить на общие и частные. Общие законы имеют место во всех явлениях природы – это закон сохранения и превращения энергии, закон всемирного тяготения, закон взаимодействия заряженных тел, закон сохранения заряда и некоторые другие. Частные законы проявляют себя при определённых условиях, для небольшого круга физических явлений. Например, закон Архимеда, закон Шарля, закон Ома.
Физика теснейшим образом связана со многими науками, являясь часто для них фундаментом, особенно для технических наук. Большинство открытий физики послужили важнейшими вехами развития техники. Например, открытие электромагнитной индукции стало базой для электротехники, открытие электромагнитных волн — для радиотехники и т.д. Но и развитие техники, способствует более быстрому развитию физики, так как техника вооружает физику новейшими приборами для исследований и подчас ставит задачи для самих исследований.
Задачи
1. Перевести
36 км/час в м/с. ![]()
2. Перевести
15 м/с в км/час ![]()
3600
3. Перевести
30 м3/мин в литры/сек ![]()
4. Перевести
10000 литров/час в м3/с ![]()
Вопросы:
1. Что в переводе с греческого означает «фюзис».
2. Что такое материя?
3. Что мы понимаем под ощущениями?
4. Каковы основные свойства материи?
5. Что такое взаимодействие?
6. К чему приводит взаимодействие?
7. Что такое физическая величина?
8. Назовите некоторые физические величины.
9. Что значит измерить физическую величину?
10. Какие виды материи вы знаете?
11. Какие виды фундаментальных взаимодействий вы знаете?
12. Какова основная функция полей?
13. Какие поля вы знаете?
14. Что такое физический закон?
Домашнее задание 1:
1. Перевести 144 км/час в м/с
2. Перевести 100 м3/час в литры/сек
3. Перевести 100 см/мин в м/с
4. Перевести 70 м/с в км/час
5. Перевести 1000 см2/мин в м2/сек
Выполнение лабораторных работ связано с измерением различных физических величин.
Измерение – нахождение значения физической величины опытным путём с помощью средств измерений.
Прямое измерение – определение значения физической величины непосредственно средствами измерения.
Косвенные измерения – определение значения физической величины по формуле, связывающей её с другими величинами, определяемыми прямыми измерениями.
При измерениях всегда появляются неточности (погрешности).
Погрешность измерения — оценка отклонения измеренного значения величины от её истинного
значения. Погрешность измерения является характеристикой (мерой) точности измерения. Чем точнее прибор, тем меньше
погрешность. Для оценки качества измерений вводят понятия относительной и
абсолютной погрешностей. Абсолютная погрешность равна Δα=|αо-α|, где αо-
истинное значение величины (табличное или измеренное более точным прибором),
α – приближённое значение этой величины, полученное при измерении.
Относительная погрешность вычисляется по формуле εα ![]() Δα100% и выражается в процентах.
Δα100% и выражается в процентах.
αo
Погрешности, возникаемые при измерениях делятся на систематические и случайные.
Систематические погрешности - это погрешности, соответствующие отклонению измеренного значения от истинного значения физической величины всегда в одну сторону (повышения или занижения). При повторных измерениях погрешность остается прежней.
Причины возникновения систематических погрешностей:
1) несоответствие средств измерения эталону;
2) неправильная установка измерительных приборов (наклон, неуравновешенность);
3) несовпадение начальных показателей приборов с нулем и игнорирование поправок, которые в связи с этим возникают;
4) несоответствие измеряемого объекта с предположением о его свойствах (наличие пустот и т.д).
Случайные погрешности - это погрешности, которые непредсказуемым образом меняют свое численное значение. Такие погрешности вызываются большим числом неконтролируемых причин, влияющих на процесс измерения (неровности на поверхности объекта, дуновение ветра, скачки напряжения и т.д.). Влияние случайных погрешностей может быть уменьшено при многократном повторении опыта.
Если систематические погрешности малы, то учитываются случайные погрешности и погрешности прибора.
Введём следующие обозначения: А, В, С, - физические величины.
![]() а
– среднестатистическое значение искомой величины
а
– среднестатистическое значение искомой величины ![]()
∆аi
– случайная погрешность отдельного измерения ![]()
![]() – среднее значение случайной погрешности,
– среднее значение случайной погрешности,
![]()
При оценке погрешности измерения необходимо учитывать не только случайную погрешность, но и погрешность прибора.
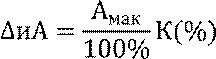
Пример: Максимальное напряжение, которое можно измерить вольт- метром по выбранной шкале, равно 500 В, класс точности K = 0.5. Для определения приборной погрешности следует вычислить
![]()
Если же неизвестен класс точности
прибора и нет других сведений о прибор- ной погрешности, то ∆иА считают равной цене наименьшего деления
шкалы (Фадеев М.А. 2002г. Элементарная обработка результатов измерения.). Общую
абсолютную погрешность результата находят по формуле: ![]()
Относительная погрешность ![]() или
или ![]()
Результат представляется следующим образом:
![]()
Эти выкладки справедливы для прямых измерений.
Для косвенных измерений
|
N o
|
Формула для физической величины |
Формула для относительной погрешности |
|
1 |
А=ВСD |
|
|
2 |
|
|
|
3 |
A=B±C |
|
|
4 |
|
|
Результаты измерений записываются следующим образом:![]()
![]() ; ɛ = ….%
; ɛ = ….%
1. Для иллюстрации работы с функцией
типа ![]() рассмотрим вычисление объема прямого кругового конуса V на основе прямых измерений его
диаметра основания d и
высоты h:
рассмотрим вычисление объема прямого кругового конуса V на основе прямых измерений его
диаметра основания d и
высоты h:
![]()
|
№ |
d (мм) |
(мм) |
∆d (мм) |
(мм) |
∆Аd (мм) |
h (мм) |
(мм) |
∆h (мм) |
(мм) |
∆Аh (мм) |
ɛd |
ɛh |
ɛV |
∆V (мм3) |
|
1 |
20 |
20 |
0 |
0,4 |
1,4 |
42 |
40 |
2 |
1,2 |
2,2 |
0,07 |
0,055 |
0,195 |
816 |
|
2 |
19 |
1 |
39 |
1 |
||||||||||
|
3 |
20 |
0 |
40 |
0 |
||||||||||
|
4 |
21 |
1 |
41 |
1 |
||||||||||
|
5 |
20 |
0 |
38 |
2 |
После проведения прямых измерений
были вычислены средние статистические значения ![]() диаметра и высоты соответственно, а также абсолютные
погрешности ∆Аd = 1,35 мм и
диаметра и высоты соответственно, а также абсолютные
погрешности ∆Аd = 1,35 мм и ![]() = 1,35 мм этих же величин.
= 1,35 мм этих же величин.
![]() = 20 – 20 = 0(мм)
= 20 – 20 = 0(мм)
∆d2=![]() –d2 = 20 – 19 = 1(мм)
–d2 = 20 – 19 = 1(мм)
![]() = 1(мм)
= 1(мм)
∆d5=![]() –d5 =
–d5 = ![]() = 0(мм)
= 0(мм)
![]() =0,4 (мм)
=0,4 (мм)
Погрешность прибора примем равной цене деления
линейки δ=1мм. ![]() = 1,4 (мм)
= 1,4 (мм)
∆h1=![]() –h1 =
–h1 = ![]() = 2(мм)
= 2(мм)
![]() = 1(мм)
= 1(мм)
∆h4=![]() –h4 =
–h4 = ![]() = 1(мм)
= 1(мм)
![]() = 2(мм)
= 2(мм)
![]() = 1,2 (мм)
= 1,2 (мм)
δ = 1(мм)
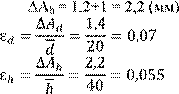
Численное значение объема
конуса ![]() вычисляется по формуле
вычисляется по формуле![]()
![]() )
)
Принимая во внимание характер
зависимости, сначала выразим относительную погрешность измерения объема конуса.
В выражении относительной погрешности пренебрежём погрешностью π: ![]()
Вычисляем абсолютную погрешность
∆V=ɛV·![]() = 0,195·4187 = 816 мм3,
тогда окончательный результат можно записать в виде:
= 0,195·4187 = 816 мм3,
тогда окончательный результат можно записать в виде:
V = (4189 ± 816) мм3 . ![]()
К систематическим погрешностям можно отнести и погрешности отсчёта. Погрешность отсчета получается от недостаточно точного отсчитывания показаний средств измерений.
В большинстве случаев абсолютную погрешность отсчета принимают равной половине цены деления. Исключения составляют измерения стрелочными часами (стрелки передвигаются рывками).
Абсолютную погрешность отсчета принято обозначать ∆оА. Например, абсолютная погрешность измерения высоты ∆оh, при измерении линейкой с ценой деления 1мм, будет равна 0,5мм.
При отсутствии случайных погрешностей полная абсолютная погрешность равна сумме погрешности отсчёта и погрешности измерительного прибора.
2. Вычислим погрешность измерения коэффициента трения с помощью динамометра. Опыт заключается в том, что брусок равномерно тянут по горизонтальной поверхности и измеряют прикладываемую силу: она равна силе трения скольжения.
![]()
С помощью динамометра взвесим брусок с грузами: N = 1,8 Н измерим силу трения Fтр=0,6 Н получаем μ=0,33.
Инструментальная погрешность динамометра (находим по таблице) составляет Δ иР
=0,05Н. Погрешность отсчета (половина цены деления)
Δ оР =0,05Н . Абсолютная погрешность измерения веса и силы трения 0,1 Н.
Относительная погрешность измерения
![]() ,
, ![]() следовательно абсолютная погрешность
косвенного измерения ∆μ составляет ∆μ = ɛ·µ =
0,22·0,33=0,074
следовательно абсолютная погрешность
косвенного измерения ∆μ составляет ∆μ = ɛ·µ =
0,22·0,33=0,074
Вывод:
При определении коэффициента трения в данной работе
получен следующий результат ![]()
3. Определить работу тока за 8 секунд при силе тока 1,5А и напряжении 4В
|
I |
U |
t |
А |
∆оI |
∆оU |
∆оt |
∆иI |
∆иU |
∆иt |
ɛ |
∆А |
|
(А) |
(В) |
(c) |
(Дж) |
(А) |
(В) |
(с) |
(А) |
(В) |
(с) |
(%) |
(Дж) |
|
1,5 |
4 |
8 |
48 |
0,05 |
0,1 |
0,2 |
0,05 |
0,15 |
1 |
44 |
21,1 |
![]() СА =0,1А; СV
=0,2В; класс точности амперметра и вольтметра К=2,5; Imax =2A;
Umax=6B
СА =0,1А; СV
=0,2В; класс точности амперметра и вольтметра К=2,5; Imax =2A;
Umax=6B
Абсолютная инструментальная погрешность амперметра равна
![]()
Абсолютная погрешность отсчета (половина цены деления) равна ∆оI = 0,05А
Абсолютная инструментальная погрешность вольтметра
равна ![]()
![]()
Абсолютная погрешность отсчета вольтметра (половина цены деления) ∆оU = 0,1B
Абсолютная погрешность отсчёта секундомера равна Δ оt = 0,5c
Абсолютная инструментальная погрешность секундомера с ценой деления Сt=1c равна
Δ иt = 0,5с
Относительная погрешность измерения работы тока равна
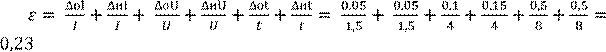
Абсолютная погрешность измерения работы тока равна
∆А = ɛ·А = 0,23·48 = 11,04 Дж. Работа тока равна А=48Дж ±11Дж при относительной погрешности ɛ = 23%
Вопросы:
1. Что означает измерить физическую величину?
2. Что такое измерение?
3. Назовите основные единицы измерения системы «СИ».
4. Какими приставками можно увеличивать единицу измерения?
5. Какими приставками можно уменьшать единицу измерения?
6. Какие бывают измерения?
7. Что такое погрешность?
8. Какие погрешности вы знаете?
9. Что такое абсолютная погрешность?
10. По какой формуле определяется относительная погрешность?
11. Какие погрешности называются систематическими?
12. Назовите причины возникновения систематических погрешностей.
13. Какие погрешности называются случайными?
14. Как найти среднестатистическое значение искомой величины?
15. Как определить абсолютную случайную погрешность отдельного измерения?
16. Как определить среднее значение случайной погрешности?
17. Как определить случайную погрешность прибора?
18. Как находится общая абсолютная погрешность измерения?
19. Чему равна относительная погрешность прямого измерения?
20. Чему равна относительная погрешность произведения?
21. Чему равна относительная погрешность степенной функции?
22. Как записывается результат измерения?
Домашнее задание 2:
1. Вычислить работу тока при напряжении 6В, силе тока 2А за 40с.
|
I |
U |
t |
А |
∆оI |
∆оU |
∆оt |
∆иI |
∆иU |
∆иt |
ɛ |
∆А |
|
(А) |
(В) |
(c) |
(Дж) |
(А) |
(В) |
(с) |
(А) |
(В) |
(с) |
(%) |
(Дж) |
|
|
|
|
|
|
|
|
|
|
|
|
|
СА =0,01А; СV =0,05В; класс точности амперметра и вольтметра К=0,5; Imax =2A;
Umax=7,5B
2. Вычислить погрешность измерения коэффициента трения с помощью динамометра и сделать вывод.
![]()
С помощью динамометра взвесим брусок с грузами: N = 3,8 Н измерим силу трения Fтр=1,3 Н
Инструментальная погрешность динамометра (находим по таблице) составляет Δ иР =0,05Н. Погрешность отсчета (половина цены деления), Δ оР =0,05Н .
 Основное
свойство материи – движение. Самое простейшее движение материи – механическое
движение. Все в мире происходит где-то и когда-то: в пространстве (где?) и во
времени (когда?). Каждое тело в любой момент времени занимает определенное
положение в пространстве относительно других тел. Если с течением времени
положение тела не изменяется, то говорят, что тело находится в покое. Если же с
течением времени положение тела изменяется, то это значит, что тело совершает
механическое движение. Механическим движением тела называется изменение его
положения в пространстве относительно других тел с течением времени.
Основное
свойство материи – движение. Самое простейшее движение материи – механическое
движение. Все в мире происходит где-то и когда-то: в пространстве (где?) и во
времени (когда?). Каждое тело в любой момент времени занимает определенное
положение в пространстве относительно других тел. Если с течением времени
положение тела не изменяется, то говорят, что тело находится в покое. Если же с
течением времени положение тела изменяется, то это значит, что тело совершает
механическое движение. Механическим движением тела называется изменение его
положения в пространстве относительно других тел с течением времени.
Изучить движение тела — значит узнать, как изменяется его положение с течением времени. Если это известно, то можно вычислить положение тела в любой момент времени. В этом и состоит основная задача механики - определять положение
 тела в любой
момент времени. Так, астрономы, пользуясь законами механики, могут
вычислять положения небесных тел друг относительно друга и с большой точностью
предсказывать такие небесные явления, как затмения Солнца или Луны.
тела в любой
момент времени. Так, астрономы, пользуясь законами механики, могут
вычислять положения небесных тел друг относительно друга и с большой точностью
предсказывать такие небесные явления, как затмения Солнца или Луны.
Чтобы решить основную задачу механики, нужно кратко и точно указать, как движется тело, как изменяется его положение с течением времени. Другими словами, надо найти математическое описание движения, установить связь между величинами, характеризующими движение.
Во многих случаях нет необходимости указывать положение каждой точки движущегося тела. Одинаково движутся все точки чемодана, который мы поднимаем с пола, кабины аттракциона «колесо обозрения» в парке, ступеньки эскалатора в метрополитене и т. д. Движение тела, при котором все его точки движутся одинаково, называется поступательным. При таком движении любая прямая, мысленно проведенная в теле, остается параллельной самой себе.
Если нас не интересует положение каждой точки твёрдого тела, например, положение корабля в океане, то тело принимается за материальную точку. Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой.
Вращательным движением называется такое движение твёрдого тела, при котором точки тела движутся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых находятся на этой оси.
Положение тела (точки) в пространстве определяется системой отчёта. В систему отсчёта входят: тело отсчета, система координат, связанная с ним, и прибор для измерения времени. Относительно выбранной системы отсчета и рассматривается любое движение.
Движение точки будет задано естественным способом, если будут известны:
1. Траектория точки;
2.
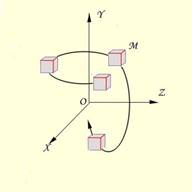
 Зависимость изменения
длины дуги от времени: ОМ=S=f(t). Эта зависимость называется уравнением
движения материальной точки.
Зависимость изменения
длины дуги от времени: ОМ=S=f(t). Эта зависимость называется уравнением
движения материальной точки.
3. Начало движения;
4. Начало отсчёта; направление отсчёта.
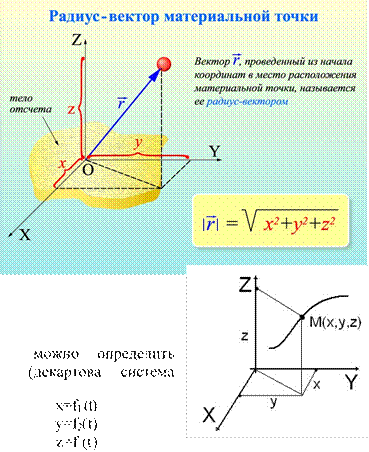
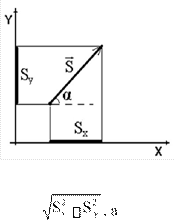
Положение точки в пространстве однозначно определяется радиусвектором 𝑟⃗ , проведённым из некоторого неподвижного центра в данную точку М. Зависимость изменения радиус-вектора от времени задаёт движение точки. Такой способ задания называется векторным. Положение точки в пространстве в этом случае будет определяться геометрическим местом концов векторов r, т.е. годографом её радиус-вектора.
𝑟⃗ = 𝑟⃗(𝑡)
При координатном способе задания движения, должны быть известны зависимости, по которым координаты точки в пространстве координат).
 3
3
Эти выражения называются уравнениями движения (зависимость координаты от времени) и выражают уравнение траектории в параметрической форме. Решая их совместно и исключая параметр t, можно получить уравнение линии. Зависимость f(x,y,z)=0 – это уравнение траектории. Перемещением тела (материальной точки) называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим
положением. Перемещение тела надо отличать от его траектории (линии вдоль которой происходит движение тела). Необходимо также ввести понятие пути. Длиной пути L называется сумма длин всех участков траектории, пройденной точкой за рассматриваемый промежуток времени.
Чтобы решить основную задачу механики необходимо знать перемещение. В системе координат вектор задаётся проекциями. Проекция вектора на ось равна Sx=Scosα, Sy=Ssinα. Модуль вектора можно найти по теореме ПифагораS
Sy
угол между вектором и осью Х равен α arctg![]()
Sx Задачи
1. Мальчик вышел из дому и прошел по прямым улицам сначала 2 квартала к востоку, а затем 2 квартала к северу (длина квартала 150 м). Определить путь и перемещение. 600м. 424м.
2. Расстояние между пунктами А и В по прямой линии 6 км. Человек проходит это расстояние туда и обратно за 2 ч. Чему равны путь и перемещение человека за 2 и 1 ч?
12км. 0,6км
3. Мячик упал с высоты 2 м, отскочил от земли и был пойман на половине высоты. Укажите величину пути и численное значение перемещения мячика.
3м. 1м.
4. Велосипедист движется равномерно по окружности радиусом 100 м и делает один оборот за 2 мин. Определите путь и перемещение велосипедиста за 1 мин и за 2 мин.
5. 314м. 200м. 628м. 0м. Дорожка имеет форму прямоугольника, меньшая сторона которого равна 21 м, а большая — 28 м. Человек обходит всю дорожку за 1 мин. Определите перемещение и путь человека за 1 мин и за 0,5 мин.
0,98м. 35м. 49м.
Вопросы:
1. Что называется механическим движением тела?
2. В чём состоит основная задача механики?
3. Что такое поступательное движение тела?
4. Что такое материальная точка?
5. Что называется вращательным движением тела?
6. Чем определяется положение тела в пространстве?
7. Что входит в систему отсчёта?
8. Какие способы задания движения вы знаете?
9. Как задаётся движение естественным способом?
10. Что такое уравнение движения при естественном способе задания движения?
11. В чём заключается векторный способ задания движения?
12. Что такое координатный способ задания движения?
13. Что такое уравнение движения при координатном способе задания движения?
14. Что такое перемещение тела?
15. Как найти перемещение при координатном способе задания движения на плоскости?
16. Что такое траектория движения?
17. Что такое путь?

 Домашнее
задание 3:
Домашнее
задание 3:
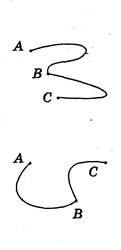
![]() По заданной траектории движения тела
найдите его перемещение
По заданной траектории движения тела
найдите его перемещение
𝑆𝐴𝐵 и 𝑆𝐴С Задачу решите графически.
2. Материальная точка движется по окружности с радиусом 2 м. Найдите путь и перемещение через 1/6 часть оборота, 1/4, 1/2 и полный оборот.
![]() 2/3π. 2. π. 2 2 . 2π. 4. 4π.
0.
2/3π. 2. π. 2 2 . 2π. 4. 4π.
0.
3. По заданной траектории движения тела найдите его перемещение
𝑆⃗𝐴𝐵. и 𝑆⃗𝐴С Задачу решите графически.
4. Автомобиль, двигаясь прямолинейно, проехал путь 10 м, затем сделал поворот, описав четверть окружности радиусом 10 м, и прошел далее по перпендикулярной улице еще 10 м. Сделайте в масштабе пояснительный чертеж, вычислите пройденный путь и найдите численное значение перемещения. 35,7м. 21,2м.
Мы рассмотрим сначала самый простой вид движения — прямолинейное равномерное движение.
Прямолинейное движение — это движение, при котором траектория тела (точки) - прямая линия. Примером может служить движение автомобиля по участку дороги, на котором нет подъемов, спусков, поворотов. А прямолинейным равномерным движением называют такое движение, при котором тело (точка) за любые равные промежутки времени совершает одинаковые перемещения. Для описания прямолинейного движения удобно направить одну из координатных осей, например ось X, вдоль той прямой, по которой движется тело.
Как найти (вычислить) перемещение тела за какой-то промежуток времени t. Для этого нужно знать перемещение тела за одну единицу времени. Скоростью равномерного прямолинейного движения называют постоянную векторную величину, равную отношению
S
перемещения
тела за любой промежуток времени к значению этого промежутка. υ ![]() Зная t
Зная t
скорость υ, мы найдем, и перемещение за любой промежуток времени t . В проекциях это выглядит так:
х Sx Sx υxt т.к. Sx xxo , то x xo υxt υ t
Выражение x xo υxt называется уравнением движения для равномерного прямолинейного движения.
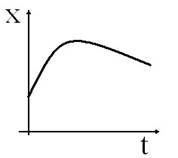
Формула x xo υxt показывает, как с течением времени изменяется координата тела (точки) при прямолинейном равномерном движении. Она, как говорят, описывает движение.
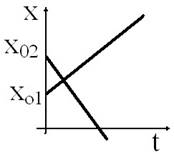 Но
описать движение тела можно и с помощью графика. Допустим, что тело (точка)
движется по некоторой прямой, вдоль горизонтальной оси отложим в масштабе
время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат)
— тоже в определенном масштабе — значения координаты тела, то полученный график
показывает, как изменяется координата тела со временем. Такой график называют
графиком движения (не следует путать с траекторией движения). График движения
есть такое же описание движения, как и формула. Для равномерного движения
графиком зависимости координаты от времени является прямая, выходящая из точки
равной начальной координате тела. Прямая наклонена под углом к оси ох, тангенс
которого равен скорости движения. Если скорость направлена вдоль оси ох, то
прямая направлена вверх. Если скорость направлена против оси – вниз.
Но
описать движение тела можно и с помощью графика. Допустим, что тело (точка)
движется по некоторой прямой, вдоль горизонтальной оси отложим в масштабе
время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат)
— тоже в определенном масштабе — значения координаты тела, то полученный график
показывает, как изменяется координата тела со временем. Такой график называют
графиком движения (не следует путать с траекторией движения). График движения
есть такое же описание движения, как и формула. Для равномерного движения
графиком зависимости координаты от времени является прямая, выходящая из точки
равной начальной координате тела. Прямая наклонена под углом к оси ох, тангенс
которого равен скорости движения. Если скорость направлена вдоль оси ох, то
прямая направлена вверх. Если скорость направлена против оси – вниз.
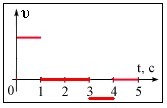 Наряду
с графиками движения часто пользуются графиками скорости. Их получают,
откладывая по оси абсцисс время, а по оси ординат - проекции скорости тела.
Такие графики показывают, как изменяется скорость с течением. В случае
прямолинейного равномерного движения «зависимость» скорости от времени состоит
в том, что скорость со временем не изменяется. Поэтому график скорости
Наряду
с графиками движения часто пользуются графиками скорости. Их получают,
откладывая по оси абсцисс время, а по оси ординат - проекции скорости тела.
Такие графики показывают, как изменяется скорость с течением. В случае
прямолинейного равномерного движения «зависимость» скорости от времени состоит
в том, что скорость со временем не изменяется. Поэтому график скорости
представляет собой прямую, параллельную оси времени
По графику скорости тоже можно определить перемещение тела за данный промежуток времени, оно численно равно площади под графиком скорости. Графическое представление движения это графики зависимости координаты от времени (перемещения от времени) и скорости от времени.
ЗАДАЧИ
1. Сколько времени потребуется скорому поезду длиной 100 м. чтобы проехать мост длиной 800 м, если скорость поезд равна 36 км/ч?
2. Один автомобиль, двигаясь равномерно со скоростью 15 м/с в течение 10 с, совершил такое же перемещение, что и другой за 25 с. Какова скорость второго автомобиля?
3.  Автомобиль,
двигаясь со скоростью 54 км/ч, проехал половину пути до места назначения за 2
ч. С какой скоростью он должен продолжать движение, чтобы достигнуть цели и
вернуться обратно за то же время?
Автомобиль,
двигаясь со скоростью 54 км/ч, проехал половину пути до места назначения за 2
ч. С какой скоростью он должен продолжать движение, чтобы достигнуть цели и
вернуться обратно за то же время?
4. Тело движется равномерно вдоль оси X. Модуль скорости равен 42 км/ч. Найдите положение тела через 15 с после начала движения, если начальная координата тела равнялась - 250 м. Чему равен путь, пройденный телом?
5. При движении вдоль прямой координата точки изменилась за 5 с от значения х 1= 8м до значения х2 = -10 м. Найти модуль скорости и направление движения точки.
6.
 Движение точки на плоскости описывается уравнениями х
= 2 + 3t, у = 2t. Определить траекторию движения точки и построить ее на
плоскости
Движение точки на плоскости описывается уравнениями х
= 2 + 3t, у = 2t. Определить траекторию движения точки и построить ее на
плоскости
ХОУ.
7. Уравнения движения двух тел заданы выражениями х1 = 12 - 6t и х2 = -9 + 3t. Найдите время и координату места встречи тел.
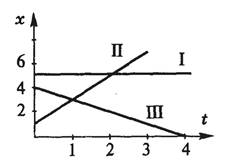
8. Написать уравнения движения тел, графики которых даны на рисунке.
9. По графику скорости записать уравнение движения, хо=0.
10. Даны уравнения движения: х1 = 3 +2t и х2 = 6 - t. Найти начальную координату, скорость, место и время встречи. Задачу решить аналитически и графически.
Вопросы:
1. Что называется прямолинейным равномерным движением?
2. Что такое скорость равномерного прямолинейного движения?
3. Что такое уравнение движения?
4. Как выглядит уравнение движения для равномерного прямолинейного движения?
5. Что является графическим представлением движения?
6. Как определить перемещение по графику зависимости скорости от времени?
ДОМАШНЕЕ ЗАДАНИЕ 4
1. По озеру буксир тянет баржу со скоростью 12 км/ч. Длина буксира с баржой 100 м. Сколько времени буксир с баржой будет проходить мимо теплохода, стоящего у пристани, если длина теплохода 50 м?
2. Поезд длиной 200 м, двигаясь равномерно, прошел мост за 1 мин. Какова скорость поезда, если длина моста 300 м?
3. Поезд длиной 100 м движется по мосту равномерно со скоростью 72 км/ч. За сколько минут он пройдет мост, если его длина 850 м?
4. Вдоль оси Х движутся две точки: первая - по закону х1 = 6 + 2t, а вторая по закону х2 = -1 + 5t. В какой момент времени они встретятся?
5. Тело движется против оси ОХ. Модуль скорости равен 36 км/ч. Начальная координата равна 10 м. Найдите положение тела через 6 с. Чему равен путь, пройденный телом?
6.
 Точка М совершает движение на плоскости ХОУ.
Координаты точки в зависимости от времени изменяются так: х = -2t, у = 3
+ 2t. Записать уравнение траектории у = у(х) точки М. Найти начальные
координаты движущейся точки и ее координаты через 2 с после начала движения.
Точка М совершает движение на плоскости ХОУ.
Координаты точки в зависимости от времени изменяются так: х = -2t, у = 3
+ 2t. Записать уравнение траектории у = у(х) точки М. Найти начальные
координаты движущейся точки и ее координаты через 2 с после начала движения.
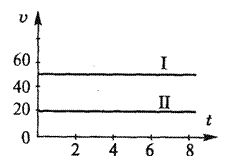
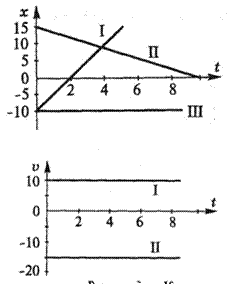
7. Написать уравнения движения тел, графики которых даны на рисунке.
8. По графику скорости записать уравнение движения. хо=0.
9. Даны уравнения движения: х1= 1+1,5t и х2= 6- 2t. Найти начальную координату, скорость, место и время встречи. Задачу решить аналитически и графически.
10. Даны уравнения движения: х1 = 10(2-t) и x2=2(-3+2t). Найти начальную координату, скорость, место и время встречи. Задачу решить аналитически и графически.
11. Даны уравнения движения: х1 = 1,5(2-t) и x2 = 1,2(t -2). Найти начальную координату, скорость, место и время встречи. Задачу решить аналитически и графически.
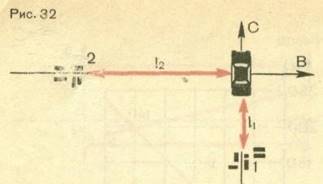 Положение
тела в пространстве всегда задается относительно какого-то другого тела — тела
отсчета. С этим телом связывают систему координат, и положение тела задается
его координатами. Но за тело отсчета можно выбрать любое тело и с каждым из них
связать систему координат. Тогда положение одного и того же
тела можно рассматривать относительно разных систем отсчета. Координаты одного
и того же тела относительно разных тел отсчета могут оказаться различными.
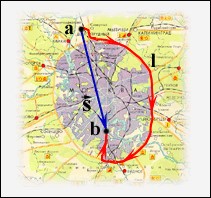
Например, положение автомобиля на дороге (рис. 32) можно задать, указав, что
он находится на расстоянии ℓ1 к северу от населенного
Положение
тела в пространстве всегда задается относительно какого-то другого тела — тела
отсчета. С этим телом связывают систему координат, и положение тела задается
его координатами. Но за тело отсчета можно выбрать любое тело и с каждым из них
связать систему координат. Тогда положение одного и того же
тела можно рассматривать относительно разных систем отсчета. Координаты одного
и того же тела относительно разных тел отсчета могут оказаться различными.
Например, положение автомобиля на дороге (рис. 32) можно задать, указав, что
он находится на расстоянии ℓ1 к северу от населенного
пункта 1. Но можно сказать, что автомобиль расположен на расстоянии ℓ2 к востоку от населенного пункта 2. Это и значит, что положение тела относительно: оно различно относительно разных систем координат. Но относительно не только положение тела. Относительно и его движение. В чем состоит относительность движения? Рассмотрим движение одного и того же тела относительно двух разных систем отсчета, движущихся одна относительно другой прямолинейно и равномерно. Одну из них мы будем условно считать неподвижной. Другая движется относительно нее прямолинейно и равномерно. Вот простой пример. Лодка пересекает реку перпендикулярно течению, двигаясь с некоторой скоростью относительно воды. Вода в реке движется относительно берега со скоростью течения реки. Представим себе, что за движением человека следят два наблюдателя: один неподвижный, расположился на берегу в точке О, другой — на плоту, плывущем по течению (со скоростью течения реки). Оба наблюдателя измеряют перемещение человека и время, затраченное на него. Относительно воды плот неподвижен, а по отношению к берегу, он движется со скоростью течения реки.
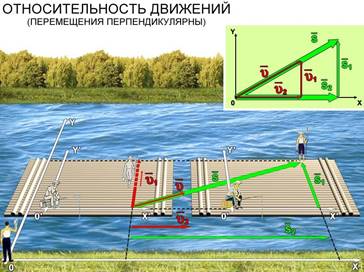 Проведем
мысленно через точку О систему координат ХОУ. Ось X направим вдоль
берега, ось У - перпендикулярно течению реки. Это неподвижная система отсчета.
Другую систему координат Х'О'У´ свяжем с плотом. Оси X' и У`
параллельны осям X и У. Это - подвижная система координат. Как движется
человек относительно наших двух систем?
Проведем
мысленно через точку О систему координат ХОУ. Ось X направим вдоль
берега, ось У - перпендикулярно течению реки. Это неподвижная система отсчета.
Другую систему координат Х'О'У´ свяжем с плотом. Оси X' и У`
параллельны осям X и У. Это - подвижная система координат. Как движется
человек относительно наших двух систем?
Наблюдатель на плоту, двигаясь вместе со «своей» системой координат по течению, видит, что человек удаляется от него к противоположному берегу все время перпендикулярно течению со скоростью υ1 , и совершает перемещение S1.
Совсем другим представится движение лодки неподвижному наблюдателю на берегу. Относительно «его» системы координат человек за то же время t совершил перемещение S. За это же время подвижная система отсчета вместе с плотом совершила перемещение S2. Схематически перемещения лодки показаны на рисунке. Из рисунков видно, что перемещение S лодки относительно неподвижной системы координат связано с перемещениями S1 и S2 формулой:
SS1 S2
Скорость υ лодки относительно неподвижной системы координат мы получим, разделив
S S S
![]() перемещение S на время t:
1
2
или υ
υ1 υ2 , это формула сложения
скоростей. t t t
перемещение S на время t:
1
2
или υ
υ1 υ2 , это формула сложения
скоростей. t t t
Скорость тела относительно неподвижной системы координат равна геометрической сумме скорости тела относительно подвижной системы координат и скорости подвижной системы относительно неподвижной.
Мы видим, что и перемещение и скорость тела относительно разных систем отсчета различны. Различны и траектории движения (СС' — относительно подвижной системы и ОС' - относительно неподвижной). В этом и состоит относительность движения.
В нашем примере мы считали неподвижной систему координат, связанную с берегом. Но мы могли бы условиться считать неподвижной систему координат, связанную с плотом. Тогда подвижным оказался бы берег и связанная с ним система координат, и мы рассматривали бы движение берега относительно плота и лодки. Формулы сложения перемещений и скоростей остались бы такими же. Мы уже и раньше говорили, что относительно не только движение, относителен и покой.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
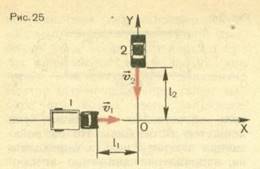 1. По
дороге навстречу друг другу движутся два автомобиля: один со скоростью 60 км/ч,
другой — 90 км/ч. У заправочной станции автомобили встретились и продолжили
свой путь. Определите положение каждого автомобиля через 30 мин после встречи и
расстояние между ними в этот момент.
1. По
дороге навстречу друг другу движутся два автомобиля: один со скоростью 60 км/ч,
другой — 90 км/ч. У заправочной станции автомобили встретились и продолжили
свой путь. Определите положение каждого автомобиля через 30 мин после встречи и
расстояние между ними в этот момент.
Решение. За начало координат примем заправочную станцию, а время будем отсчитывать от момента встречи автомобилей. Координатную ось X направим по направлению движения первого автомобиля. Тогда координаты автомобилей через 0,5 ч после встречи можно вычислить по формулам: х = хо + υxt
Начальные координаты хо1 и хо2 у обоих автомобилей равны нулю. Поэтому х1 = 60•0,5 =
30 (км), х2 = - 90•0,5 = 45 (км). Расстояние между автомобилями равно разности их координат ℓ = х1 – х2 = 30-(-45) = 75 (км)
2. Два автомобиля движутся по взаимно перпендикулярным дорогам, но направлению к перекрестку. В некоторый момент времени первый автомобиль, скорость υ1 которого равна 27 км/ч, находится на расстоянии ℓ1 = 300 м от перекрестка. Второй в тот же момент времени находится на расстоянии ℓ2 = 450 м от перекрестка. С какой скоростью υ2 движется второй автомобиль, если он достигает перекрестка через t= 5 с после первого?
Решение. За начало отсчета координат примем перекресток дорог, а отсчет времени начнем с момента, когда автомобили находились на расстояниях ℓ1 и ℓ2 от перекрестка Оси координат направим вдоль дорог. Первый автомобиль движется вдоль оси X, второй — противоположно направлению оси У. Поэтому при движении первого автомобиля изменяется со временем только координата х. Ее найдем по формуле: х = х0 + υ1t, 0 = -ℓ1 + υ1t1.
Для второго автомобиля y = yo – υ2(t1 + t), 0 = ℓ2 - υ2(t1 + t), решая совместно эти два
![]() уравнения, получим: υ2 2 2 υ2 4507,5
10 м/с
уравнения, получим: υ2 2 2 υ2 4507,5
10 м/с
1 t 1 υ1t 300 37,5 υ1
ВОПРОСЫ:
1. Чем определяется положение тел в пространстве?
2. Что такое система отсчёта?
3. Может ли координата быть отрицательной величиной?
4. Может ли изменение координаты быть отрицательной величиной?
5. Наблюдения показали: за время матча футболист пробежал 12 км. Что это - перемещение или путь?
6. Штурман, определяя утром положение корабля, обнаружил, что корабль находится в точке, расположенной на 100км к северу от пункта, в котором находился накануне вечером.
Что это – перемещение или путь?
7. Автомобиль движется к востоку со скоростью 40км/ч. Другой автомобиль движется к югу со скоростью 40км/ч. Можно ли сказать, что скорости автомобилей равны?
8. Можно ли зная начальное положение тела и его путь, найти конечное положение тела?
9. Как связать скорость тела с изменением его положения при движении?
10. В чем состоит относительность движения?
11. Как в примере с лодкой движутся вода и берег относительно лодки?
12. Комбайн, убирающий в поле хлеб, движется относительно земли со скоростью 2,5 км/ч и, не останавливаясь, ссыпает зерно в автомашину. Относительно какого тела отсчета автомашина движется и относительно какого покоится?
ДОМАШНЕЕ ЗАДАНИЕ 5:
1. Двигатель самолета сообщает ему скорость относительно воздуха, равную 900 км/ч. С какой скоростью движется самолет относительно Земли при попутном ветре, скорость которого равна 50 км/ч; при таком же встречном ветре?
2. Автомобиль движется в западном направлении со скоростью 80 км/ч. Другой автомобиль движется ему навстречу с такой же скоростью. В некоторый момент расстояние между автомобилями равно 10 км. Сколько времени пройдет до момента встречи автомобилей?
3. Самолет, стартовав в Москве, держит по компасу курс на север, летя на высоте 8 км со скоростью 720 км/ч. Какими будут координаты самолета относительно аэропорта через 2 часа после старта, если во время полета дует западный ветер со скоростью 10 м/с?
4. Скорость первого автомобиля относительно второго 100 км/ч. Определите скорость второго автомобиля относительно Земли, если скорость первого относительно Земли 60 км/ч. Автомобили движутся навстречу друг другу.
5. Скорость течения реки 1 км/ч. Моторная лодка идет против течения со скоростью 10 км/ч (относительно земли). С какой скоростью она будет двигаться по течению (относительно земли и относительно воды)?
6. Велосипедист едет со скоростью 30 км/ч. Скорость ветра 3 м/с. Определите скорость ветра относительно велосипедиста, если: а) ветер встречный; б) ветер боковой.
7. Неравномерное движение. Средняя скорость.
В реальной жизни при движении тел скорость не постоянна. При движении из состояния покоя автобус, например, увеличивает свою скорость, т.е. движется неравномерно, а при остановке тормозит – уменьшает свою скорость. В некоторых случаях, когда имеют дело с неравномерным движением, пользуются средней скоростью. Ее получают, разделив перемещение тела S на время, в течение которого оно совершено:
S
υср t
Если, например, поезд, двигаясь по прямой, проходит 600 км за 10 ч, то это значит, что в среднем он за каждый час проходит 60 км. Но ясно, что какую-то часть времени поезд вовсе не двигался, а стоял на остановке; трогаясь со станции, поезд увеличивал свою скорость, приближаясь к ней — уменьшал ее. Все это при определении средней скорости мы не принимаем во внимание и считаем, что поезд каждый час проходил по 60 км, каждые полчаса — по 30 км и т.д. Пользуясь формулой, мы, как бы считаем, что поезд двигался равномерно со скоростью 60 км/ч, хотя, быть может, за все эти 10 ч не было ни одного такого часа, за который поезд прошел бы именно 60 км. Знание средней скорости позволяет найти перемещение по формуле
Sυсрt .
Но надо помнить, что эта формула дает верный результат только для того участка траектории, для которого определена средняя скорость. Если, пользуясь значением средней скорости в 60 км/ч, вычислять перемещение поезда не за 10 ч, а за 2, 4 или 5 ч, то мы получим неверный результат. Средняя скорость за время 10 ч не равна средним скоростям за 2, 4 или 5 ч.
Таким образом, средняя скорость, вообще говоря, не позволяет вычислять перемещение, а значит, и координаты в любой момент времени.
ЗАДАЧИ
1. На горизонтальном участке пути автомобиль ехал со скоростью 72 км/ч в течение 20 мин, а затем проехал подъем со скоростью 36 км/ч за 40 мин. Чему равна средняя скорость на всем пути?
2. Автомобиль проехал первую половину пути со скоростью 40 км/ч, а вторую — со скоростью 60 км/ч. Определить среднюю скорость его движения.
3. Из одного пункта в другой мотоциклист двигался со скоростью 70 км/ч, обратный путь им был пройден со скоростью 15 м/с. Определите среднюю скорость мотоциклиста за все время движения.
4. Пешеход часть пути прошел со скоростью 4 км/ч, затратив на это 2/3 времени своего движения. За оставшуюся треть времени он прошел остальной путь со скоростью 5 км/ч. Определите среднюю скорость.
5. Скорость поезда между двумя пунктами равна 80 км/ч, средняя скорость на всем пути 60 км/ч, причем остановки занимают время 1 час. Найти расстояние между этими пунктами.
6. Автомобиль проехал половину пути со скоростью 60 км/ч, оставшуюся часть пути он половину времени шел со скоростью 15 км/ч, а последний участок — со скоростью 45 км/ч. Найти среднюю скорость автомобиля на всем пути.
7. Велосипедист ехал из одного города в другой. Половину пути он проехал со скоростью 12 км/ч. Далее половину оставшегося времени он ехал со скоростью б км/ч, а затем до конца пути шел пешком со скоростью 4 км/ч. Определить среднюю скорость движения велосипедиста на всем пути.
8. Самолет летит из пункта А в пункт В и возвращается назад в пункт А. Скорость самолета в безветренную погоду равна υ. Найти отношение средних скоростей всего перелета для двух случаев, когда во время перелета ветер дует: а) вдоль линии АВ; б) перпендикулярно линии АВ. Скорость ветра равна и.
![]() υ2 и2
υ2 и2
υ
9. Расстояние между двумя станциями 4 км. Поезд метро проходит со средней скоростью 54 км/ч. При этом на разгон он затрачивает время 30 с. Затем поезд идет равномерно некоторое время и на замедление до полной остановки тратит время 20 с. Построить график скорости движения поезда и определить наибольшую скорость поезда υmax?
Вопросы:
1. Какое движение называется неравномерным?
2. Какая скорость называется средней?
3. Почему средняя скорость не всегда решает основную задачу механики?
ДОМАШНЕЕ ЗАДАНИЕ 6
1. Двигаясь по шоссе, велосипедист проехал 90 м со скоростью 15 м/с, а затем по плохой дороге 40 м со скоростью 10 м/с. С какой средней скоростью он проехал весь путь?
2. Велосипедист проехал первую половину пути со скоростью 15 км/ч, а вторую половину пути со скоростью υ2. Как велика эта скорость, если известно, что средняя скорость его движения на всем пути равна 10 км/ч?
3. Скорость поезда на подъеме 20 км/ч, а на спуске — 80 км/ч. Определите среднюю скорость на всем участке пути, если спуск в два раза длиннее подъёма?
4. На первой половине пути автобус двигался со скоростью, в 8 раз большей, чем на второй. Средняя скорость автобуса на всем пути 16 км/ч. Определить скорость автобуса на обеих половинах пути.
5. Поезд первую половину пути шел со скоростью в 1,5 раза большей, чем вторую половину пути. Средняя скорость поезда на всем пути 43,2 км/ч. Каковы скорости поезда на первой и второй половинах пути?
6. Первую половину времени тело движется со скоростью 30 м/с под углом 30° к заданному направлению, а вторую — 120° к тому же направлению со скоростью 40 м/с. Найти среднюю скорость перемещения. Какой путь тело пройдет за время 4 с?
7. Расстояние между двумя станциями 9 км. Поезд метро проходит со средней скоростью 36 км/ч. При этом, на разгон он затрачивает время 25 с. Затем поезд идет равномерно некоторое время и на замедление до полной остановки тратит время 15 с. Построить график скорости движения поезда и определить наибольшую скорость поезда υmax?
8. Из городов А и В, расстояние между которыми L = 120 км, одновременно выехали навстречу две автомашины, скорости которых постоянны и равны υ1 = 20 км/ч, υ2= 60 км/ч. Машины, пройдя каждая 120 км, остановились. 1) Найти, через какое время t и на каком расстоянии ℓ от города С, находящегося на полпути между А и В, встретятся автомашины. 2) Решить задачу графически. 3) Построить график зависимости расстояния ℓ между машинами от времени t.
9. Один паровоз прошел половину пути S со скоростью υ1 = 80 км/ч, а другую половину — со скоростью υ2 = 40 км/ч. Другой паровоз шел половину времени t со скоростью υ1 = 80 км/ч, а половину времени — с υ2 = 40 км/ч. Какова средняя скорость каждого паровоза?
8. РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ. МГНОВЕННАЯ СКОРОСТЬ. УСКОРЕНИЕ.
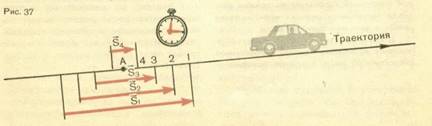 Средняя
скорость, не позволяет вычислять перемещение, а значит, и координаты в любой
момент времени. Для вычисления положения тела в любой момент времени Необходимо
знать мгновенную скорость.
Средняя
скорость, не позволяет вычислять перемещение, а значит, и координаты в любой
момент времени. Для вычисления положения тела в любой момент времени Необходимо
знать мгновенную скорость.
Мгновенная скорость. Всякое движущееся тело обладает скоростью. С другой стороны, при своем движении по траектории тело проходит через все ее точки. А таких
точек бесконечно много. Через каждую из них тело проходит в определенный момент времени. Таких моментов времени тоже бесконечно много. Выходит поэтому, что в каждый момент времени и в каждой точке траектории тело обладает какой-то скоростью. Вот эта скорость и называется мгновенной. Мгновенной скоростью тела называется скорость тела в данный момент времени или в данной точке траектории.
При прямолинейном равномерном движении скорость тела равна отношению его перемещения к промежутку времени, за который это перемещение совершено.
Допустим, что некоторое тело (как всегда, мы имеем в виду определенную точку тела) движется прямолинейно, но не равномерно. Нас интересует мгновенная скорость, например, в точке А его траектории (рис. 37). Выделим небольшой участок S1 на этой траектории, включающий точку А. Малое перемещение тела на этом участке обозначим через s1 а малый промежуток времени, в течение которого оно совершено, через t1. Разделив S1 на t1, мы получим среднюю скорость на этом участке; это именно средняя скорость, потому что скорость непрерывно изменяется, и в разных местах участка она разная. Уменьшим теперь длину участка. Выберем участок 2 (см. рис. 37), тоже включающий точку А. Перемещение теперь равно S2 (S2<S1), и совершает его тело за меньший промежуток времени t2. На этом участке скорость успевает измениться на меньшую величину. Но отношение дает нам и теперь среднюю скорость на этом меньшем участке. Еще меньше изменение скорости на протяжении участка 3 (также включающего в себя точку A). Будем продолжать уменьшать промежуток времени, за который мы рассматриваем перемещение тела. Вместе с ним будет уменьшаться и перемещение. В конце концов, промежуток времени станет так мал, что можно будет пренебречь изменением скорости за это время (движение станет как бы равномерным). Участок траектории, пройденный за этот, совсем уже малый, промежуток времени как бы стянется в точку А, а промежуток времени — в момент времени. Тогда-то средняя скорость и станет мгновенной скоростью тела в точке А.
Мгновенная скорость, или скорость в данной точке, равна пределу отношения перемещения на участке траектории, примыкающем к этой точке, к промежутку времени, в течение которого это перемещение совершается, при ∆t стремящемся к нулю.
, или первой производной перемещения по времени dt .
⃗ʋ⃗ = ⃗S⃗/
Мгновенная скорость — это векторная величина. Вектор мгновенной скорости направлен по касательной к траектории движения в данной точке. В дальнейшем, говоря о скорости неравномерного движения, мы будем иметь в виду именно мгновенную скорость.
О мгновенной скорости можно говорить и в случае равномерного движения. Разница только в том, что при равномерном движении мгновенная скорость в любой точке и в любой момент времени одна и та же. При неравномерном же движении она в разных точках и в различные моменты времени различна.
Мы видели раньше, что для вычисления координаты тела в любой момент времени нужно знать, как быстро она изменяется, т. е. каково ее изменение за единицу времени. Быстрота изменения координаты равна, как мы видели, проекции скорости на соответствующую координатную ось. Точно так же для вычисления скорости в любой момент времени нужно знать, как быстро изменяется скорость, насколько она изменяется за единицу времени. Быстрота изменения скорости называется ускорением. Мгновенное ускорение
|
a dυ dt |
![]() равно
𝑎⃗
= ⃗ʋ⃗/
равно
𝑎⃗
= ⃗ʋ⃗/
Равнопеременное движение. Для простоты мы будем
рассматривать такое неравномерное движение, при котором скорость тела за каждую единицу времени и вообще за любые равные промежутки времени изменяется одинаково. Такое движение называют равнопеременным. Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называется равнопеременным движением.
Если в некоторый начальный момент времени скорость тела равна υо, а через промежуток времени t она оказывается равной υ, то ускорение для равноускоренного движения найдём по формуле:
|
t |
∆υ⃗⃗
![]() ⃗
⃗
Ускорением тела при его равнопеременном движении называется величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Ускорение - величина векторная.
Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно разгоняется) или быстро теряет ее (при торможении).
За единицу ускорения в СИ принимается ускорение такого равноускоренного движения, при котором за 1 с скорость тела изменяется на 1 м/с. Следовательно, в СИ ускорение выражается в метрах в секунду за секунду или в метрах на секунду в квадрате (м/с2).
Проекции скорости и ускорения. Мы уже говорили, что при вычислениях нужно пользоваться формулами, в которые входят не векторы, а их проекции на оси координат.
υх υ
![]() ах ох
ах ох
При прямолинейном движении t .
υ υо аt , υx υox аxt
Если вектор ускорения, ⃗а⃗ сонаправлен вектору ⃗𝜐⃗⃗ , ⃗ʋ⃗ ↑↑ 𝑎⃗, то скорость увеличивается. Такое движение называется равноускоренным. При торможении вектор 𝑎⃗ направлен противоположно вектору ⃗𝜐⃗⃗ . ⃗ʋ⃗ ↑↓ 𝑎⃗ Это равнозамедленное движение.
Если скорость тела с течением времени уменьшается, (тело тормозит), то в какой-то момент времени скорость тела может стать равной нулю. Как оно движется после этого? Ясно, что, когда какая-либо величина, изменяясь, проходит через значение нуль, она изменяет свой знак на противоположный. В нашем случае изменяет знак скорость. Это значит, что после того, как скорость тела станет равной нулю, оно начнет двигаться в противоположном направлении.
Вопросы:
1. Какая физическая величина называется мгновенной скоростью?
2. Как находится мгновенная скорость?
3. Как направлен вектор скорости?
4. Что называется ускорением?
5. Как находится мгновенное ускорение?
6. Какое движение называется равнопеременным?
7. Как найти ускорение при равнопеременном движении?
8. Как определить скорость при равнопеременном движении?
9. Какое движение называется равноускоренным?
10. Какое движение называется равнозамедленным?
9. ПЕРЕМЕЩЕНИЕ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОПЕРЕМЕННОМ ДВИЖЕНИИ.
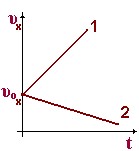
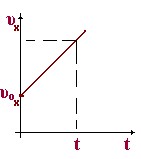 Формулу
для вычисления перемещения проще всего получить графическим методом. При
равноускоренном движении тела вдоль оси X скорость изменяется со временем
согласно формуле υx
υox axt . Так как время в эту формулу входит в первой
степени, то график для проекции скорости в зависимости от времени представляет
собой прямую, как это показано на рисунке. Прямая 1 на этом рисунке
соответствует
Формулу
для вычисления перемещения проще всего получить графическим методом. При
равноускоренном движении тела вдоль оси X скорость изменяется со временем
согласно формуле υx
υox axt . Так как время в эту формулу входит в первой
степени, то график для проекции скорости в зависимости от времени представляет
собой прямую, как это показано на рисунке. Прямая 1 на этом рисунке
соответствует
движению с положительной проекцией ускорения (скорость растет), прямая 2 — движению с отрицательной проекцией ускорения (скорость убывает). Оба графика относятся к случаю, когда в момент времени to = 0, тело имеет некоторую начальную скорость υо. Перемещение выражается площадью, заключённой под графиком. Перемещение за все время t численно равно площади трапеции. Площадь же трапеции, как известно из геометрии, равна
![]() Sx
υox υx t
Sx
υox υx t
произведению полусуммы ее оснований на высоту 2 , но υx υox аxt ,
|
a t2 Sx υoxt x 2 |
отсюда .
Таким образом, мы видим, что при равноускоренном движении перемещение растет со временем не так, как при равномерном движении: теперь в формулу входит квадрат времени. Это значит, что перемещение со временем растет быстрее, чем при равномерном движении и графиком зависимости координаты от времени является парабола.
Как зависит от времени координата тела? Теперь легко получить и формулу для вычисления координаты х в любой момент времени для тела, движущегося равноускоренно.
|
a t2 x xo υoxt x 2 |
Sx xxo , отсюда x xo Sx . Поэтому .
Для вычисления перемещения можно получить и другую полезную формулу, в которую время не входит.
|
|
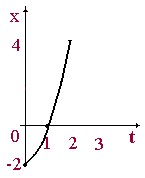 Из выражения υx
υox аxt получим выражение для t и подставим его в
формулу для перемещения, приведенную выше. Тогда получаем:
Из выражения υx
υox аxt получим выражение для t и подставим его в
формулу для перемещения, приведенную выше. Тогда получаем:
Эти формулы позволяют найти перемещение тела, если известны ускорение, а также начальная и конечная скорости движения.
Формулу перемещения можно получить, решая дифференциальное уравнение. Пусть тело движется с постоянным ускорением ⃗а⃗.
По определению a dυ → adt dυ , интегрируя обе части уравнения, получим dt
adt dυ →υ υo аt , или ![]() υо аt ,
υо аt ,
0 υo dt
Умножим обе части уравнения на dt,
dS υodtаtdt интегрируя ещё раз, получим dS υodtatdt →
0 0 0
|
S υot at2 2 |
2 2
Графическим представлением равнопеременного движения являются графики зави-
|
a t 2 x xo υoxt x 2 |
симости координаты от времени ,
скорости от времени υx υox аxt и ускорения от времени ах = const.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
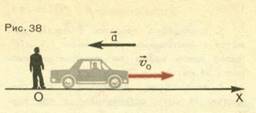
1. Автомобиль проезжает мимо наблюдателя, двигаясь со скоростью ТО м/с. В этот момент водитель нажимает на тормоз и автомобиль начинает двигаться с ускорением, по модулю равным 1,0 м/с2. Сколько времени пройдет до остановки автомобиля?
Решение. Выберем за начало отсчета координаты место нахождения наблюдателя, а координатную ось направим в сторону движения автомобиля (рис. 38). Обозначим скорость автомобиля в момент, когда он проходит мимо наблюдателя, через υо, а его ускорение после включения тормоза через а. Воспользуемся формулой υx υox аxt. В момент остановки υx
= 0. Ускорение при торможении направлено против скорости т.е. отрицательно. Следовательно, 0 = υох - ахt или t = υox/ax. Подставив в это выражение значения υox и аx, получим t = 10/1=10(c).
2. Тело движется прямолинейно с уменьшающейся скоростью. Ускорение а постоянно и по модулю равно 4 м/с2. В некоторый момент времени модуль скорости тела υ0 = = 20 м/с. Найдите скорость тела через t1 = = 4с и t2 = 8с после этого момента.
Решение. Направим координатную ось X по направлению вектора скорости υо. Тогда проекция υох положительна и равна модулю вектора υо . А так как скорость тела уменьшается, то проекция ускорения ах отрицательна и равна ах= - а.
Чтобы найти проекцию скорости в указанные в задаче моменты времени применим формулуυx υox аxt .Отсюда для момента времени t1 найдем: υ1=20 - 4•4 = 4(м/c), υ2=20 - 4•8 = -12(м/c),
Знак «минус» означает, что к исходу 8-й секунды тело двигалось в направлении, противоположном начальному. Очевидно, что перед тем, как начать движение в обратном направлении, тело должно было остановиться. В какой момент времени t это произошло? Проекция υ равна нулю, когда υ0х= - ахt. Отсюда t' = -20/-4=5 (с). Направление движения изменилось на обратное через 5 с после того момента, когда скорость тела была равна 20 м/с.
Двигаться так, как описано в этой задаче, могло бы, например, тело, которое толкнули вверх по наклонной плоскости.
3. Водитель автомобиля, движущегося со скоростью 72 км/ч, увидев красный свет светофора, нажал на тормоз. После этого скорость автомобиля стала уменьшаться на 5 м/с каждую секунду. Найдите расстояния, которые автомобиль проходит в первые 2 с после начала торможения и до полной его остановки.
Решение. Координатную ось X направим по направлению движения автомобиля (рис. 38), а за начало отсчета координаты примем то место на дороге, где началось торможение. Начало отсчета времени отнесем к моменту, когда водитель нажал на тормоз. Начальная скорость υо автомобиля со направлена с осью X, а ускорение направлено в противоположную сторону, так что проекция начальной скорости υох положительна, а проекция ускорения ах — отрицательна. Расстояния, пройденные автомобилем,— это проекции перемещения Sx,
S(2) υoxt axt2 S(2) 202 522 30(м)
2 → 2 ;
![]()
![]()
![]() полное υ2x υox2 → Sполное
υox2 → S
202
40(м)
полное υ2x υox2 → Sполное
υox2 → S
202
40(м)
-2ax -2ax полное -25
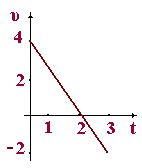 2. Определите
перемещение тела, график проекции скорости которого, показан на рисунке
2. Определите
перемещение тела, график проекции скорости которого, показан на рисунке
Решение: Перемещение равно площади под графиком скорости. За первые две секунды тело двигалось вдоль оси Х, а за третью секунду – против оси Х. Поэтому перемещение тела равно разности площадей треугольников. S = S042 – S23(-2), S = 2•4/2-1•2/2=
3(м).
ВОПРОСЫ:
1. Что такое ускорение и для чего его нужно знать?
2. При любом неравномерном движении изменяется скорость. Как ускорение характеризует это изменение?
3. Чем отличается «замедленное» прямолинейное движение от «ускоренного»?
4. Что такое равноускоренное движение?
5. Может ли тело двигаться с большой скоростью, но с малым ускорением?
6. Как направлен вектор ускорения при прямолинейном неравномерном движении?
7. Скорость - векторная величина, и изменяться может как модуль скорости, так и направление вектора скорости. Что именно изменяется при прямолинейном равноускоренном движении?
8. Может ли скорость движения тела быть равной нулю, а ускорение не равно нулю?
9. Чем отличается график скорости равномерного прямолинейного движения от графика скорости равноускоренного движения?
10. Как по графику проекции скорости равноускоренного движения определяют проекцию перемещения тела?
11. Чем различаются зависимости перемещения от времени при равномерном и равноускоренном движениях?
12. Что является графиком зависимости скорости от времени при равнопеременном движении?
13. Что представляет собой график зависимости координаты от времени при равнопеременном движении?
14. Что представляет собой график зависимости ускорения от времени при равнопеременном движении?
15. Как называются зависимости координаты от времени, скорости от времени, ускорения от времени?
16. Как называются графики зависимости координаты от времени, скорости от времени, ускорения от времени?
17. По каким формулам можно рассчитать перемещение при равнопеременном движении?
18. По какой формуле можно определить мгновенную скорость при равнопеременном движении?
19. По какой формуле рассчитывается ускорение при равнопеременном движении?
20. Что такое рывок в кинематике? Чему равен рывок? Является ли такое движение равнопеременным?
ДОМАШНЕЕ ЗАДАНИЕ 7
1. Троллейбус, трогаясь с места, движется с постоянным ускорением 1,5 м/с . Через какое время он приобретает скорость 54 км/ч?
2. Автомобиль, движущийся со скоростью 36 км/ч, останавливается при торможении в течение 4 с. С каким постоянным ускорением движется автомобиль при торможении?
3. Автомобиль, двигаясь с постоянным ускорением, на некотором участке пути увеличил свою скорость с 15 до 25 м/с. За какое время произошло это увеличение, если ускорение автомобиля равно 1,6 м/с .
4. Какая скорость движения была бы достигнута, если бы тело в течение 0,5 ч двигалось с ускорением 10 м/с2 при начальной скорости, равной нулю?
5. Постройте в координатных осях (υх, t) графики зависимости скорости от времени, для двух тел, движущихся равнопеременно: одно с возрастающей по модулю скоростью, другое — с убывающей. Начальные скорости и ускорения тел соответственно равны: 1 м/с и 0,5 м/с2; 9 м/с и 1,5 м/с2. Какой путь пройдет второе тело до остановки? Через какое время скорости обоих тел станут одинаковыми, и какой путь пройдет за это время первое тело?
6. На рисунке 44 изображены графики проекций скоростей движения трех тел, каков характер движения этих тел? Что можно сказать о скоростях движения тел в моменты времени, соответствующие точкам А и В графика? Определите ускорения и напишите выражения для скорости и перемещения этих тел.
7. Пользуясь приведенными на рисунке 45 графиками проекций скоростей трех тел,
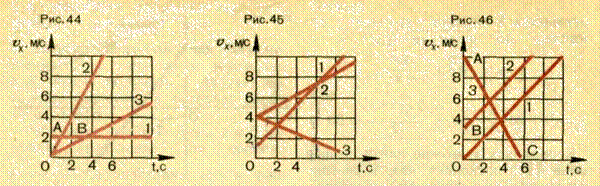
выполните следующие задания: а) определите ускорения этих тел; б) составьте для каждого тела формулу зависимости скорости от времени; в) найдите, в чем сходны и в чем различаются движения, соответствующие графикам 2 и 3?
8. На рисунке 46 приведены графики проекций скоростей движений трех тел. По этим графикам: а) определите, чему соответствуют отрезки ОА, ОВ и ОС на осях координат; 6) найдите ускорения тел; в) напишите выражения для скорости и перемещения каждого тела.
9. Самолет при взлете проходит взлетную полосу за 15 с и в момент отрыва от земли имеет скорость 100 м/с. С каким ускорением двигался самолет по взлетной полосе и какова ее длина?
10. Снаряд, летящий со скоростью 1000м/с, пробивает стенку блиндажа за 0,001 с, и после этого его скорость оказывается равной 200м/с. Считая движение снаряда в толще стенки равноускоренным, найдите ее толщину.
11. Ракета движется с ускорением 45 м/с' и к некоторому моменту времени достигает скорости 900 м/с. Какой путь она пройдет в следующие 2,5 с?
12. На каком расстоянии от Земли оказался бы космический корабль через 30 мин после старта, если бы он все время двигался прямолинейно с ускорением 9,8 м/с2 ?
13. Наблюдения показали, что скаковая лошадь достигает наибольшей скорости 15 м/с после того, как она, приняв старт, «разгонится» на протяжении 30м. Считая, что лошадь скачет с постоянным ускорением, найдите это ускорение.
14. Чтобы оторваться от земли, самолет должен набрать скорость 180 м/с. На каком расстоянии от места старта на взлетной полосе самолет достигает этого значения скорости, если его ускорение постоянно и равно 2,5 м/с2?
РЕШЕНИЕ ЗАДАЧ
1. Через 20 с после начала движения спидометр автомобиля показал скорость движения 72 км/ч. С каким ускорением двигался автомобиль?
2. За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,4 м/с2, пройдет 30 м?
3. Какую скорость будет иметь тело через 20 с от начала движения, если ускорение его движения равно 360 м/мин2?
4. Поезд метро, отходя от станции, может развить скорость 36 км/ч за 20 с. Определить ускорение его движения. Какой путь при этом поезд проходит?
5. Велосипедист, движущийся со скоростью 2 м/с, начинает спускаться с горы с ускорением 0,6 м/с2. Найдите длину горы, если спуск занял 10 с.
6. Начав торможение с ускорением 0,3 м/с2, поезд прошел до остановки 250 м. Какова была его скорость перед началом торможения?
7. Пуля, летящая со скоростью 300м/с, ударяет в земляной вал и проникает в него на глубину 56 см. Сколько времени двигалась она внутри вала? С каким ускорением? Какова была ее скорость на глубине 20 см?
8. Тело, имея начальную скорость 3 м/с, двигалось равноускоренно и приобрело, пройдя некоторое расстояние, скорость 12 м/с. Какова была скорость тела на половине этого расстояния?
9. По наклонной доске пустили катиться снизу вверх шарик. На расстоянии 50 см от начала пути шарик побывал дважды: через 2 с и через 4 с после начала движения. Определите начальную скорость и ускорение.
10. Тело, имея начальную скорость 2 м/с, прошло за пятую секунду путь, равный 8 м. Определить ускорение и путь, пройденный телом за 10 с.
ДОМАШНЕЕ ЗАДАНИЕ 8
1. Два велосипедиста едут навстречу друг другу. Первый, имея скорость 36 км/ч, начал подниматься в гору с ускорением 0,2 м/с2, а второй, имея скорость 9 км/ч, стал спускаться с горы с ускорением 0,2 м/с2. Через сколько времени и в каком месте они встретятся, если длина горы 100 м?
2. Санки скатываются с горы длиной 72 м в течение 12 с. Определите ускорение саней и скорость их в конце пути.
3. Пуля, летящая со скоростью 400 м/с, ударяет в земляной вал и проникает в него на глубину 36 см. Сколько времени двигалась она внутри вала? С каким ускорением? Какова была ее скорость на глубине 18 см?
4. Тело, имея начальную скорость 1 м/с, двигалось равноускорено и приобрело, пройдя некоторое расстояние, скорость 7 м/с. Какова была скорость тела на половине этого расстояния?
5. При равноускоренном движении из состояния покоя тело проходит за пятую секунду 90 см. Определить перемещение тела за седьмую секунду?
6.
 |
7. Два автомобиля вышли с остановки через время 1 мин один после другого и шли с ускорением 0,4 м/с2 каждый. Через какое время после выхода первого автомобиля расстояние между ними станет 2 км?
8. По наклонной доске пустили катиться снизу вверх шарик. На расстоянии 30 см от начала пути шарик побывал дважды: через 1 с и через 2 с после начала движения. Определите начальную скорость и ускорение.
10. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПО ОКРУЖНОСТИ. ЦЕНТРОСТРЕМИТЕЛЬНОЕ УСКОРЕНИЕ.
Криволинейное
движение более сложное, чем
Допустим, что тело движется по ней из точки А в точку В. Пройденный телом при этом путь — это длина дуги АВ, а перемещение — это вектор, направленный по хорде АВ. Теперь мы не можем сказать, что скорость всегда направлена вдоль вектора перемещения. Но проведем между точками А и В ряд хорд и представим себе, что тело движется именно по этим хордам. На каждой из них тело движется прямолинейно, и вектор скорости направлен вдоль хорды, т. е. вдоль вектора перемещения (рис. 52). Мгновенная скорость - по касательной. Сделаем наши прямолинейные участки более короткими (рис. 53). По-прежнему на каждом из них вектор скорости направлен вдоль хорды. Но видно, что эта ломаная линия уже больше походит на плавную кривую.
Продолжая уменьшать длину прямолинейных участков (и, конечно, увеличивая их число), мы как бы стягиваем их в точки, и ломаная линия превращается в плавную кривую.
Скорость же в каждой точке оказывается направленной по касательной к кривой в этой точке (рис. 54).
 В
том, что скорость при криволинейном движении действительно направлена по
касательной, убеждает нас, например, наблюдение за работой на точиле (рис. 55).
Если прижать к вращающемуся точильному камню конец стального прутка, то
раскаленные частицы, отрывающиеся от камня, будут видны в виде искр. Эти
частицы летят с той скоростью, которой они обладали в момент отрыва от камня.
Хорошо видно, что направление движения искр совпадает с касательной к
окружности в той точке, где пруток касается камня. По касательной движутся и
брызги от колес буксующего автомобиля (рис. 56). Таким образом, мгновенная
скорость тела в разных точках криволинейной траектории имеет различные
направления. Но даже если по модулю скорость тела не изменяется, ее все же
нельзя считать постоянной. Ведь скорость — величина векторная. А для векторных
величин модуль и направление одинаково важны, поэтому криволинейное движение —
это всегда движение с ускорением, даже если по модулю скорость постоянна. Мы
ограничимся рассмотрением именно такого криволинейного движения —
криволинейного движения с постоянной по модулю скоростью. Его называют
равномерным криволинейным движением. Ускорение при таком движении связано с
изменением направления скорости. Как направлено и чему равно это ускорение?
В
том, что скорость при криволинейном движении действительно направлена по
касательной, убеждает нас, например, наблюдение за работой на точиле (рис. 55).
Если прижать к вращающемуся точильному камню конец стального прутка, то
раскаленные частицы, отрывающиеся от камня, будут видны в виде искр. Эти
частицы летят с той скоростью, которой они обладали в момент отрыва от камня.
Хорошо видно, что направление движения искр совпадает с касательной к
окружности в той точке, где пруток касается камня. По касательной движутся и
брызги от колес буксующего автомобиля (рис. 56). Таким образом, мгновенная
скорость тела в разных точках криволинейной траектории имеет различные
направления. Но даже если по модулю скорость тела не изменяется, ее все же
нельзя считать постоянной. Ведь скорость — величина векторная. А для векторных
величин модуль и направление одинаково важны, поэтому криволинейное движение —
это всегда движение с ускорением, даже если по модулю скорость постоянна. Мы
ограничимся рассмотрением именно такого криволинейного движения —
криволинейного движения с постоянной по модулю скоростью. Его называют
равномерным криволинейным движением. Ускорение при таком движении связано с
изменением направления скорости. Как направлено и чему равно это ускорение?
Криволинейное движение — движение по дугам окружностей. Изменение скорости по направлению при криволинейном движении должно, конечно, зависеть от формы траектории. А различных форм кривых линий есть бесчисленное множество. Но оказывается, не нужно рассматривать движения по каждой отдельной кривой.
На рисунке 62 показана некоторая сложная криволинейная траектория. Из рисунка видно, что отдельные части криволинейной траектории представляют собой приблизительно дуги окружностей. Движение по любой криволинейной траектории можно приближенно представить как движение по дугам некоторых окружностей. Поэтому задача нахождения ускорения при равномерном криволинейном движении сводится к отысканию ускорения при равномерном движении тела по окружности.
Равномерное движение по окружности — это движение с ускорением, хотя по модулю скорость не изменяется. Наша задача выяснить, как направлено и чему равно это ускорение.
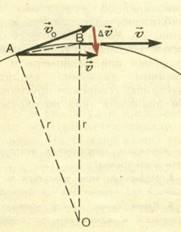
Докажем, что вектор ускорения направлен к центру окружности. Ускорение, как
известно, определяется равенством dt t .
Обозначим для краткости разность двух значений скорости ∆υ.
Ясно, что вектор а направлен так же, как вектор Δυ , потому что t — величина скалярная.
Допустим, что тело движется по окружности радиусом г и в некоторый момент времени, который мы примем за начальный (t = 0), оно находится в точке А. Скорость υo в этой точке направлена по касательной. Рассмотрим еще одну точку, очень близкую к точке А, — точку В, в которой тело, двигаясь по окружности, окажется через очень малый промежуток времени t. Будем считать, что точки A и В настолько близки друг к другу, что дуга АВ неотличима от хорды АВ, хотя на рисунке это и нельзя изобразить. Но как бы точка В ни была близка к точке А, скорость υ в точке В все же отличается от скорости υ направлением, хотя и не отличается от нее по модулю (υ = υ0). Теперь мы можем найти вектор ∆υ: перенесем вектор υ параллельно самому себе так, чтобы он и вектор υо исходили из точки А, и соединим концы обоих векторов отрезком прямой, направив его от υо к υ. Получившийся направленный отрезок и есть вектор ∆υ. Из рисунка видно, что вектор ∆υ направлен внутрь окружности. И если точки А и В будут предельно близки друг к другу, то вектор ∆υ, перенесенный в точку А, будет направлен к центру окружности. Туда же будет
направлен и вектор ускорения а . Таким образом, при равномерном движении тела по окружности его ускорение во всех точках окружности «устремлено» к ее центру. Его так и называют центростремительным ускорением. Обозначим его а.
Ускорение тела, равномерно движущегося по окружности в любой ее точке, центростремительное, т. е. направлено по радиусу окружности к ее центру. В любой точке вектор ускорения перпендикулярен вектору скорости. Эта особенность ускорения при равномерном движении по окружности показана на рисунке 61.
Чему равен модуль центростремительного ускорения? Числовое значение (модуль) ускорения мы легко найдем из рисунка 60. Треугольник, составленный из векторов υо, и υ, равнобедренный, так как υ = υо. Треугольник ОАВ на том же рисунке тоже равнобедренный, потому что стороны ОА и ОВ — радиусы окружности. Углы при вершинах обоих треугольников равны, так как они образованы взаимно перпендикулярными сторонами. Поэтому треугольники подобны, как равнобедренные с равными углами при вершинах. Из
Δυ υ АВ r
![]() подобия треугольников следует
пропорциональность сходственных сторон: .
Но,
подобия треугольников следует
пропорциональность сходственных сторон: .
Но,
как указывалось раньше, если точки А и В очень близки друг к другу, то хорда АВ неотличима от дуги АВ. Длина же дуги АВ - это путь, пройденный телом с по-
Δυ υ υt t
![]() стоянной по модулю
скоростью υ. Он равен υt. Поэтому можно написать:
или
стоянной по модулю
скоростью υ. Он равен υt. Поэтому можно написать:
или
![]()
![]() Δυ υ2 , т.е. a υ2 . Таким образом, при
равномерном движении по окружности во всех t r r
Δυ υ2 , т.е. a υ2 . Таким образом, при
равномерном движении по окружности во всех t r r
ее точках ускорение по модулю одно и то же - а. Но направлено оно всегда по радиусу к центру (см. рис. 61), так что направление ускорения от точки к точке изменяется. Равномерное движение по окружности нельзя назвать равноускоренным.
Напомним, что равномерное движение по окружности нас интересовало потому, что всякое движение по криволинейной траектории можно представить как движение по дугам окружностей различных радиусов.
Теперь мы можем сказать, что в любой точке криволинейной траектории тело движется с ускорением, направленным к центру той окружности, частью которой является участок траектории, содержащий эту точку. Модуль же ускорения зависит от скорости тела и от радиуса соответствующей окружности. На рисунке 62 показана некоторая сложная траектория, по которой движется тело, и центростремительные ускорения тела в различных ее точках.
В общем случае, когда скорость меняется и по модулю и по направлению вектор ускорения направлен под некоторым углом к вектору скорости. Обычно его представляют
![]()
![]() как сумму двух составляющих ааτ аn , тангенсальное ускорение aτ и направлено оно
по касательной к траектории и характеризует изменение модуля скорости aτ υtυо , an υr2 направлено по радиусу кривизны нормальное
ускорение (центростремительное)
как сумму двух составляющих ааτ аn , тангенсальное ускорение aτ и направлено оно
по касательной к траектории и характеризует изменение модуля скорости aτ υtυо , an υr2 направлено по радиусу кривизны нормальное
ускорение (центростремительное)
2 2 arctgan .
![]() траектории.
а а а . Угол между скоростью и
ускорением равен: α
траектории.
а а а . Угол между скоростью и
ускорением равен: α
τ n aτ
ВОПРОСЫ
1. Что такое путь при движении по окружности?
2. Что является перемещением при движении по окружности?
3. Как направлена скорость при криволинейном движении?
4. Как направлено центростремительное ускорение?
5. Чему равен модуль центростремительного ускорения?
6. Что характеризует тенгенсальное ускорение?
7. Чему равно полное ускорение тела, движущегося по окружности?
8. Как определить тангенсальное ускорение?
9. Как вычислить полное ускорение?
Домашнее задание 9
1. Автомобиль движется по закруглению дороги радиусом 120 м со скоростью 36 км/ч. Чему равно центростремительное ускорение автомобиля?
2. Радиус одного колеса 15 см, другого - 30 см, а линейные скорости точек на ободе колес соответственно равны 2,5 и 7,5м/с. Во сколько раз центростремительное ускорение точек на ободе одного колеса больше, чем на ободе другого?
3. Конькобежец движется со скоростью 12 м/с по окружности радиусом 50 м. Определите центростремительное ускорение при движении конькобежца.
4. С какой скоростью и в каком направлении должен лететь самолет над экватором на высоте Н, чтобы для него Солнце находилось все время на одной и той же высоте.
5. Шкив радиусом 20 см приводится во вращение грузом, подвешенным на нити, постепенно сматывающейся со шкива. В начальный момент груз был неподвижен, а затем стал опускаться с ускорением 2 см/с2. Найдите ускорение точки А в этот момент. Блок невесом, нить нерастяжима.
![]()
11. ПЕРИОД И ЧАСТОТА
ОБРАЩЕНИЯ. УГЛОВАЯ СКОРОСТЬ. СВЯЗЬ УГЛОВОЙ И ЛИНЕЙНОЙ СКОРОСТЕЙ.
![]() Движение
тела по окружности часто характеризуют не скоростью υ движения тела, а
угловой скоростью ω (омега) и промежутком времени, за который тело
совершает один полный оборот - период обращения Т. При равномерном вращении
угловая скорость находится как угол поворота радиус вектора ∆𝜑 или ω d
.
Движение
тела по окружности часто характеризуют не скоростью υ движения тела, а
угловой скоростью ω (омега) и промежутком времени, за который тело
совершает один полный оборот - период обращения Т. При равномерном вращении
угловая скорость находится как угол поворота радиус вектора ∆𝜑 или ω d
.
делённый на время поворота
Если взять полный угол поворота (2π), то время
будет равно периоду Т.![]() , а
, а
![]() . Так, например, в сообщениях о запуске очередного искусственного
спутника
. Так, например, в сообщениях о запуске очередного искусственного
спутника
Земли указывается именно период его обращения, а не скорость его движения по орбите. Но если известен период обращения Т, то легко найти и модуль скорости υ. Действительно, за время, равное периоду Т, тело проходит путь, равный длине окружности L=2πr, где r — радиус окружности, по которой движется тело T 2πr Отсюда линейная скорость равна υ
2πr υ . Движение тела (точки) по окружности, можно характеризовать еще одной величиT ной — числом оборотов по окружности в единицу времени. Ее называют частотой обращения и обозначают буквой n или f. n 1 Измеряется в об/сек или в Гц (Герц).
T
Центростремительное ускорение можно теперь найти по формуле а4π2n2r . Теперь можно сказать, что чем дальше от центра окружности, тем больше ускорение точек.
Вращательное движение твёрдого тела вокруг оси можно представить как движение множества точек. Скорости и ускорения точек будут различны. Чем дальше от оси, тем скорость и ускорения точек будут больше. А вот угловые характеристики для всех точек одинаковы. Поэтому при вращательном движении чаще пользуются угловыми характеристиками.
Период и угловая скорость связаны соотношением T ![]() . Угловая и линейная
. Угловая и линейная
скорость связаны соотношением υ ωr . В случае, когда угловая скорость не постоянна, а dω
изменяется с постоянной скоростью (угловое ускорение ε ![]() ), то по аналогии с
), то по аналогии с
dt t
|
εt2
|
прямолинейным движением можно записать:.
Это и есть уравнения движения для вращающегося тела.
ВОПРОСЫ
1. Что называется угловой скоростью?
2. Как определить угловую скорость при равномерном движении по окружности?
3. Что такое период?
4. По каким формулам можно рассчитать период вращения?
5. Как определить линейную скорость?
6. Что такое частота вращения?
7. Как выглядит уравнение движения для тела вращающегося вокруг неподвижной оси?
Домашнее задание 10
1. Частота обращения ветроколеса ветродвигателя 30 об/мин, якоря электродвигателя 1500 об/мин, барабана сепаратора 8400 об/мин, шпинделя шлифовального станка 96000 об/мин. Вычислить их периоды.
2. Найти частоту обращения Луны вокруг Земли.
3. Скорость точек рабочей поверхности наждачного круга диаметром 300 мм не должна превышать 35 м/с. Допустима ли посадка круга на вал электродвигателя, совершающего 1400 об/мин; 2800 об/мин?
4. Частота обращения воздушного винта самолета 1500 об/мин. Сколько оборотов делает винт на пути 90 км при скорости полета 180 км/ч?
5. Период обращения платформы карусельного станка 4 с. Найти скорость крайних точек платформы, удаленных от оси вращения на 2 м.
6. Радиус рукоятки колодезного ворота в 3 раза больше радиуса вала, на который наматывается трос. Какова линейная скорость конца рукоятки при поднятии ведра с глубины 10 м за 20 с?
7. При увеличении в 4 раза радиуса круговой орбиты искусственного спутника Земли период его обращения увеличивается в 8 раз. Во сколько раз изменяется скорость движения спутни ка по орбите?
8. Минутная стрелка часов в 3 раза длиннее секундной. Найти отношение скоростей концов стрелок.
9. Циркулярная пила имеет диаметр 600 мм. На ось пилы насажен шкив диаметром 300 мм, который приводится во вращение посредством ременной передачи от шкива диаметром 120 мм, насаженного на вал электродвигателя. Какова скорость зубьев пилы, если вал двигателя совершает 1200 об/мин?
10. Диаметр колеса велосипеда «Пенза» d = 70 см, ведущая зубчатка имеет zx = 48 зубцов, а ведомая z2 = 18 зубцов. С какой скоростью движется велосипедист на этом велосипеде при частоте вращения педалей п = 1 об/с? С какой скоростью движется велосипедист на складном велосипеде «Кама» при той же частоте вращения педалей, если у этого велосипеда соответственно d = 50 см, zl = 48 зубцов, z2 = 15 зубцов?
11. Каково центростремительное ускорение поезда, движущегося по закруглению радиусом 800 м со скоростью 20 м/с?
12. Скорость точек экватора Солнца при его вращении вокруг своей оси равна 2 км/с. Найти период обращения Солнца вокруг своей оси и центростремительное ускорение точек экватора.
13. Период обращения молотильного барабана комбайна «Нива» диаметром 600 мм равен 0,046 с. Найти скорость точек, лежащих на ободе барабана, и их центростремительное ускорение.
14. ![]() С
какой скоростью автомобиль должен проходить середину выпуклого моста радиусом
С
какой скоростью автомобиль должен проходить середину выпуклого моста радиусом
40 м, чтобы центростремительное ускорение было равно ускорению свободного падения?
15. Найти центростремительное ускорение точек колеса автомобиля, соприкасающихся с дорогой, если автомобиль движется со скоростью 72 км/ч и при этом частота обращения колеса 8 с-1.
16. ![]() Радиус
рабочего колеса гидротурбины в 8 раз больше, а частота обращения в 40 раз
меньше, чем у паровой турбины. Сравнить скорости и центростремительные
ускорения точек обода колес турбин.
Радиус
рабочего колеса гидротурбины в 8 раз больше, а частота обращения в 40 раз
меньше, чем у паровой турбины. Сравнить скорости и центростремительные
ускорения точек обода колес турбин.
17. Детский заводной автомобиль, двигаясь равномерно, прошел расстояние s за время t. Найти частоту обращения и центростремительное ускорение точек на ободе колеса, если диаметр колеса равен d.
18. Кольцо радиусом R катится без скольжения по горизонтальной поверхности с угловой скоростью ω. Найти зависимость координат точки кольца от времени. Начальные условия: XO= 0, уo = 0.
19. С какой скоростью должен ехать автомобиль, чтобы сорвавшийся с его колеса в точке А застрявший в шине камешек попал в ту же точку колеса, от которой оторвался? Радиус колеса 20 см.
20. Цилиндр радиусом R вращается между двумя параллельными рейками, движущимися в одну сторону со скоростями υ1> υ2 (скольжение отсутствует). Найти угловую скорость вращения цилиндра и скорость его центра.
21. Катушка с намотанной на ней нитью лежит на горизонтальном столе и может катиться по нему без скольжения. Внутренний радиус катушки г, внешний R.
С какой скоростью и в каком направлении будет перемещаться ось катушки, если конец нити тянуть в горизонтальном направлении со скоростью υ?
22. Круглый диск радиусом R катится без скольжения по горизонтальной плоскости. Угловая скорость диска равна ω. Найти скорость точек А, В, С, О диска в данный момент.
12. РАСЧЁТ ФРИКЦИОННЫХ, РЕМЁННЫХ И ЗУБЧАТЫХ ПЕРЕДАЧ.
Механическими передачами или просто передачами называют механизмы, служащие для передачи энергии движения, как правило, с изменением скоростей, моментов сил и с преобразованием видов и законов движения. По принципу работы передачи делятся на: передачи трением с непосредственным контактом тел качения (фрикционные а) и с
гибкой связью (ремённые г) передачи зацеплением с непосредственным контактом (зубчатые б, червячные в и винт-
гайка е) и с гибкой связью (цепные д).
Фрикционные передачи – это передачи, в которых движение от ведущего вала к ведомому передаётся силами трения покоя при непосредственном контакте фрикционных дисков, находящихся на этих валах. При этом линейные скорости крайних точек равны.
![]() υ1
= ω1R1; υ2 = ω2R2
, отсюда передаточное число (отношение угловой скорости ведомого вала к
угловой скорости ведущего вала) рано i = ω2/ω1
или i = R1/R2
υ1
= ω1R1; υ2 = ω2R2
, отсюда передаточное число (отношение угловой скорости ведомого вала к
угловой скорости ведущего вала) рано i = ω2/ω1
или i = R1/R2
Фрикционные передачи с плавным изменением передаточного числа называются вариаторами.
Ремённая передача широко применяется для передачи движения между удалёнными валами. Она осуществляется посредством шкивов, закреплённых на валах и надетых на эти валы плоских или клиновидных ремней. При этом передачи называются плоскоремёнными и клиноремёнными.
К недостаткам передач относятся большие габариты, непостоянство передаточного числа из-за проскальзывания.
К достоинствам бесшумность.
Без учёта проскальзывания скорость ремня и линейные скорости крайних точек валов равны. Поэтому передаточное число находится по аналогичным формулам. i = ω2/ω1 или i = R1/R2
Зубчатая передача является механизмом, который с помощью зубчатого зацепления передаёт или преобразует движение с изменением угловых скоростей и моментов сил.
Для передачи вращения между параллельными валами используют цилиндрические зубчатые колёса. Для передачи вращения между пересекающимися валами используют конические зубчатые колёса, для передачи вращения между перекрещивающимися - зубчатовинтовые колёса.
Передаточное число равно
![]()
Задачи
1. Определить радиус якоря электродвигателя, делающего 1200 об/мин, если линейная скорость его обмотки не должна превышать 12,56 м/с
2. Линейная скорость точек, лежащих на окружности точильного камня, равна 12,56 м/с, а его диаметр равен 0,8 м. Определить период вращения, частоту вращения, угловую скорость камня.
3. Диаметр фрикционного диска ведущего вала, 40 см, угловая скорость 6 рад/с. Диаметр ведомого диска 0,8 м. Определить угловую скорость ведомого вала, линейную скорость крайних точек ведущего и ведомого дисков и передаточное число.
4.
![]() Частота вращения ведущей шестерни 10Гц. Число зубьев 50.
Определить частоту вращения ведомой шестерни, если число зубьев её 150.
Частота вращения ведущей шестерни 10Гц. Число зубьев 50.
Определить частоту вращения ведомой шестерни, если число зубьев её 150.
5. Грузы 1 и 2 прикреплены к тросам, намотанным на ступенчатый барабан с радиусами ступеней R=0,6м, r=0,2м м. Груз 1 опускается с постоянным ускорением а1 =
3 м/с2 и имеет в данный момент времени скорость υ0 = 6 м/с. Определить в этот же момент времени угловые скорость и ускорение барабана, скорость и ускорение груза 2 и точки А барабана.
Ответ: ω = 10 рад/сек. ɛ = 5 рад/сек2 , υ2 = υA = 2 м/с, a2 = 1 м/с2, aA = 20,02 м/с2.
6. В ременной передаче шкив диаметра D1 = 500 мм начинает вращаться из состояния покоя с постоянный угловым ускорением 0,1рад/c2, приводя во вращение шкив диаметра D2 = 300 мм. Через какое время после пуска шкив диаметра D2 будет обладать угловой скоростью, соответствующей 200 об/мин? Ответ: 40 с.
Вопросы:
1. Что называется механическими передачами?
2. Как делятся передачи по принципу работы?
3. Какие передачи называются фрикционными?
4. Что такое вариатор?
5. Что такое плоскоремённая передача?
6. Как называется передача с помощью клиновидного ремня?
7. По какой формуле находится передаточное число фрикционных и ремённых передач?
8. Какая передача называется зубчатой?
9. Чему равно передаточное число зубчатой передачи?
10. Какие бывают зубчатые колёса?
ДОМАШНЕЕ ЗАДАНИЕ 11
1. Диаметр фрикционного диска ведущего вала, 30 см, угловая скорость 5 рад/с. Диаметр
![]() ведомого
диска 0,6 м. Определить угловую 3 скорость ведомого
вала, линейную скорость крайних точек ведущего и ведомого дисков и передаточное
число.
ведомого
диска 0,6 м. Определить угловую 3 скорость ведомого
вала, линейную скорость крайних точек ведущего и ведомого дисков и передаточное
число.
2. Частота вращения ведущей шестерни 5Гц. Число зубьев 50. Определить частоту вращения ведомой шестерни, если число зубьев её 100. В зубчатой передаче движение от ведущего колеса 1 радиуса 0,2 м через блок колес 2 передается колесу
3 радиуса 0,8 м Определить угловую скорость колеса 3 в момент времени 2 с, если колесо 1 вращается согласно закону φ = 4t3 , r1 = 0,2м, R2 = 0,6м, r2 = 0,3м, R3 = 0,8м. Ответ: ω3 = 6 рад/сек.
13. КАК ИЗМЕНЯЮТСЯ КООРДИНАТЫ ТЕЛА СО ВРЕМЕНЕМ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ПО ОКРУЖНОСТИ.
Допустим, что некоторое тело равномерно движется по окружности радиусом г. Систему координат удобно (хотя и необязательно) выбрать так, чтобы начало координат совпадало с центром окружности, а оси X и Y были направлены вдоль двух взаимно перпендикулярных диаметров (рис. 63).
Пусть при своем движении тело в какой-то момент времени находится в точке М на окружности. Координата х в этот момент равна отрезку ОА на горизонтальном диаметре, а координата у — отрезку ОВ на вертикальном.
х = rсоsφ, y = rsinφ или с учётом угловой скорости х = rсоsωt, y = rsinωt.
Тригонометрические функции являются периодическими. Координаты повторяются через промежуток времени, который называется период обращения Т. Тело снова окажется в точке М и его координаты х и у будут снова равны ОА и ОВ соответственно. Такими же они будут и через два периода, и через три периода и т. д. Это и есть главная особенность движения по окружности — координаты тела через каждый период обращения повторяются.
Равномерное движение по окружности— это периодическое движение. Из того, что мы уже знаем о скорости и ускорении тела, равномерно движущегося по окружности, ясно, что и эти величины тоже изменяются периодически: через каждый период повторяются и численные значения, и направления скорости и ускорения.
Такого рода периодические изменения величин называют колебаниями.
![]() Построение графиков х
= rсоsφ с помощью окружности.
Построение графиков х
= rсоsφ с помощью окружности.
Начертим окружность радиуса R. Разделим её на равные части, например, на 32 части. Начертим систему координат (х,φ), та, чтобы ось φ походила через центр окружности. На оси φ отложим отрезки дуг и опустим в них перпендикуляры. Через точки на окружности проведём вспомогательные
прямые, параллельные оси φ. Получим искомые точки синусоиды плавно соединим их.
Получили график функции х=sinφ
ВОПРОСЫ:
1. Как направлена мгновенная скорость при криволинейном движении?
2. Чем различаются изменения скорости при прямолинейном и криволинейном движениях?
3. Могут ли при криволинейном движении совпадать направления векторов скорости и ускорения?
4. Может ли тело двигаться по криволинейной траектории без ускорения?
5. Какая связь между криволинейным движением и движением по окружности?
6. Как направлено ускорение тела, движущегося по окружности с постоянной по модулю скоростью?
7. Можно ли считать центростремительное ускорение постоянным, а равномерное движение по окружности равноускоренным?
8. Если при движении тела по окружности модуль скорости изменяется, будет ли ускорение тела направлено к центру окружности?
9. Катер со спортсменом на водных лыжах движется по окружности. Спортсмен может следовать за катером по той же окружности, но может двигаться и вне и внутри окружности. Каково соотношение скоростей спортсмена и катера в этих трех случаях?
10. Что такое период обращения?
11. Что такое частота обращения?
12. Как связаны между собой период и частота обращения?
13. Как выражается центростремительное ускорение через период обращения?
14. Как выражается центростремительное ускорение через частоту обращения?
15. Точильный круг радиусом 10 см делает один оборот за 0,2 с. Найдите скорость точек, наиболее удаленных от оси вращения.
16. Автомобиль движется по закруглению дороги радиусом 100 м. Чему равно центростремительное ускорение автомобиля, если он движется со скоростью 54 км/ч?
17. Период обращения первого космического корабля — спутника Земли «Восток» равнялся 90 мин. Средняя высота спутник; над Землей была равна 320 км. Радиус Земли 6400 км. Вычислите скорость корабля.
18. Какова скорость движения автомобиля, если его колеса радиусом 30 см делают 600 оборотов в минуту?
19. Луна движется вокруг Земли на расстоянии 380 000 км от нее, совершая один оборот за 27,3 сут. Вычислите центростремительное ускорение Луны.
ДОМАШНЕЕ ЗАДАНИЕ 12
1. Автомобиль движется по закруглению дороги радиусом 220 м со скоростью 72 км/ч. Чему равно центростремительное ускорение автомобиля?
2. Вал диаметром 30 см при вращении делает один оборот за 0,6 с. Определите линейную скорость точек на поверхности вала
3. Диск диаметром 60 см равномерно перекатывают на расстояние 8 м за 4 с. Какова угловая скорость вращения диска?
4. Радиус одного колеса 30 см, другого - 60 см, а линейные скорости точек на ободе колес соответственно равны 2,5 и 7,5м/с. Во сколько раз центростремительное ускорение точек на ободе одного колеса больше, чем на ободе другого?
5. Пропеллер самолета радиусом 2 м вращается при посадке с частотой 1500 мин-1, посадочная скорость самолета относительно Земли равна 144 км/ч. Определите скорость точек на конце пропеллера. Какова траектория движения этой точки?
6. Найти радиус вращающегося колеса, если известно, что линейная скорость точки лежащей на ободе в 4 раза больше линейной скорости точки, лежащей на 6 см ближе к оси колеса.
7. Первая в мире орбитальная космическая станция двигалась со скоростью 7,8 км/с и имела период обращения 88,85 мин. Считая ее орбиту круговой, найти высоту станции над поверхностью Земли. Радиус Земли принять равным 6400 км.
8. Постройте график функции х=2соsφ
9. Постройте график функции х=3соs(φ+π/6)
10. Постройте график функции х=2sinφ +1
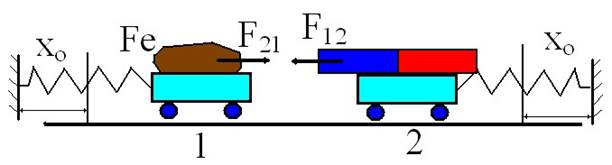
Физические объекты проявляют себя в движении и взаимодействии. Мерой взаимодействия тел или частиц, из которых состоят тела, является сила. Результатом взаимодействия тел является либо деформация (изменение размеров), либо ускорение (изменение скорости). Каждое из этих проявлений силы может быть использовано для её измерения. Измерить величину деформации часто проще, чем измерить ускорение. Поэтому основной деталью прибора для измерения сил – динамометра – является пружина, степень деформации которой зависит от величины измеряемой силы.
Рассмотрим опыт по взаимодействию магнита с куском железа (смотри рисунок). Динамометры, прикреплённые к обоим телам, регистрируют одинаковые по величине деформации. Это значит, что действие одного тела на другое равно действию другого тела на первое. То есть сила действия одного тела на другое равна силе действия второго на первое.
Это III закон Ньютона. F12 F21
Опираясь на этот закон можно определять силу, действующую на одно тело с помощью измерения силы действующей на другое тело.
Из практики известно, что чем большую деформацию мы желаем создать, тем большее усилие нужно приложить к деформируемому телу. При малых деформациях величина деформации пропорциональна приложенной силе (закон Гука).
F = k(ℓ − ℓ0) = kΔℓ
где F – абсолютная величина силы, ℓо – первоначальная длина тела, ℓ - длина
деформированного тела и К – коэффициент упругости.
Из закона Гука следует, что шкала динамометра должна быть равномерной.
Всякая сила имеет направление, причём результат действия силы зависит не только от её величины, но и от направления силы. Например, ударяя по мячу в разные стороны, футболист сообщает мячу ускорение разного направления. Сила – векторная величина.
В реальности на тело могут действовать множество сил. Сила, действие которой эквивалентно действию всех сил, действующих на тело, называется равнодействующей всех сил. Если линии действия сил сходятся в одной точке, то такая совокупность сил называется системой сходящихся сил (пучком сил). Равнодействующая системы сходящихся сил, действующих на тело равна геометрической сумме сил. k
⃗F⃗ = ∑ ⃗F⃗i i=1
![]() Силы
могут быть сосредоточенными, действующими в одной точке
и распределёнными, действующими на определённую часть поверхности.
Силы
могут быть сосредоточенными, действующими в одной точке
и распределёнными, действующими на определённую часть поверхности.
Автомобиль, стоящий на мосту – сосредоточенная сила, действующая на мост. Поезд, проходящий по мосту - распределённая сила (нагрузка).
![]() Вычислить
силу можно по ускорению, которое тело приобретает под действием этой силы. Из
курса физики 7 класса известно, что сила тяжести равна F=mg, где m – масса тела, g – ускорение
свободного падения. Масса входящая в эту формулу называется
гравитационной, т.к. является мерой взаимодействия
тела с Землёй.
Вычислить
силу можно по ускорению, которое тело приобретает под действием этой силы. Из
курса физики 7 класса известно, что сила тяжести равна F=mg, где m – масса тела, g – ускорение
свободного падения. Масса входящая в эту формулу называется
гравитационной, т.к. является мерой взаимодействия
тела с Землёй.
Рассмотрим движение тела по окружности. Тело движется равномерно по окружности радиуса R с угловой скоростью ω под действием силы упругости F=kx определяемой с помощью динамометра. Под действием этой силы тело приобретает центростремительное ускорение а=ω2R. Проделав опыты с телами различной массы, убедимся, что сила пропорциональна массе и центростремительному ускорению. Масса, входящая в данную формулу называется инертной т.к. влияет на изменение скорости движения. Будем считать, что инертная и гравитационная массы равны. Причём произведение массы на центростремительное ускорение будет равно силе, которую показывает динамометр. Эта сила называется центростремительной. 𝐹⃗ = 𝑚𝑎⃗. Эта формула выражает II закон Ньютона (основной закон динамики поступательного движения). Итак силу можно измерить по изменению движения, то есть по ускорению.
![]() Если
действующие на материальную точку можно заменить одной силой - равнодействующей
системы сил, то возможно и обратное действие – силу, действующую на
материальную точку можно разложить на несколько сил, сумма которых равна данной
силе. Например: на кронштейне подвешено тело. Его вес действует на точку
подвеса. Чтобы найти силы, возникающие в стержнях необходимо разложить силу
веса по направлениям, параллельным стержням. Тогда 𝐹⃗ 1, является
растягивающей силой, а 𝐹⃗
2 сжимающей
силой. Из подобия треугольников следует:
Если
действующие на материальную точку можно заменить одной силой - равнодействующей
системы сил, то возможно и обратное действие – силу, действующую на
материальную точку можно разложить на несколько сил, сумма которых равна данной
силе. Например: на кронштейне подвешено тело. Его вес действует на точку
подвеса. Чтобы найти силы, возникающие в стержнях необходимо разложить силу
веса по направлениям, параллельным стержням. Тогда 𝐹⃗ 1, является
растягивающей силой, а 𝐹⃗
2 сжимающей
силой. Из подобия треугольников следует: ![]()
![]() .
.
ВОПРОСЫ:
1. Как проявляют себя физические объекты?
2. Что является результатом взаимодействия тел?
3. Что такое сила?
4. Как можно измерить силу?
5. Сформулируйте III закон Ньютона.
6. Сформулируйте закон Гука.
7. Что означает выражение «сила – векторная величина»?
8. Что называется равнодействующей сил?
9. Чему равна равнодействующая сходящихся сил?
10. Какие бывают силы?
11. Сформулируйте II закон Ньютона
1. Под действием силы пружина, жёсткостью 1кН/м растянулась на 1см. Определить модуль силы.
2. Под действием какой силы пружина, имеющая жесткость 10000 Н/м, сжалась на 4 см?
3. Чему равна жесткость латунного стержня, если под действием груза 1000 Н он удлинился на 1 мм?
4. Определите удлинение пружины, если на нее действует сила 10 Н, а жесткость пружины 500 Н/м.
5. Паровоз толкнул вагон массой 30 т, стоящий на горизонтальном пути. Вагон начал двигаться со скоростью 0,5 м/с. Определите силу удара, если его длительность 1 с.
6. Снаряд массой 15 кг при выстреле приобретает скорость 600 м/с. Найдите среднюю силу, с которой пороховые газы давят на снаряд, если длина ствола орудия 1,8 м. Движение снаряда в стволе считайте равноускоренным.
7. На кронштейне подвешено тело весом 10Н. АВ=30см, ВС= 60см АС=70см. Определить реакции связи (силы упругости в стержнях). Начертите чертёж.
8. На кронштейне подвешено тело весом 10Н. АВ=30см, ВС= 50см АС=40см. Определить реакции связи (силы упругости в стержнях). Начертите чертёж.
ДОМАШНЕЕ ЗАДАНИЕ 13
1. Под действием силы пружина, жёсткостью 2кН/м растянулась на 4см. Определить модуль силы.
2. Чему равна жесткость латунного стержня, если под действием груза 2000 Н он удлинился на 0,5 мм? Пружина жесткостью 100 Н/м под действием силы удлинилась на 5 см. Какова жесткость другой пружины, которая под действием такой же силы удлинилась на 1 см?
3. Паровоз толкнул вагон массой 30 т, стоящий на горизонтальном пути. Вагон начал двигаться со скоростью 0,5 м/с. Определите силу удара, если его длительность 1 с.
4. За какое время тело массой 100 г изменит свою скорость от 5 м/с до 15 м/с под действием силы 0,5 Н?
5. Снаряд массой 15 кг при выстреле приобретает скорость 600 м/с. Найдите среднюю силу, с которой пороховые газы давят на снаряд, если длина ствола орудия 1,8 м. Движение снаряда в стволе считайте равноускоренным.
6. На кронштейне подвешено тело весом 20Н. АВ=30см, ВС= 50см АС=60см. Определить реакции связи (силы упругости в стержнях). Начертите чертёж.
7. На кронштейне подвешено тело весом 30Н. АВ=40см, ВС= 60см АС=40см. Определить реакции связи (силы упругости в стержнях). Начертите чертёж.
15. ИМПУЛЬС. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА. II ЗАКОН НЬЮТОНА. ВЗАИМОДЕЙСТВИЕ ДВУХ ИЛИ НЕСКОЛЬКИХ ТЕЛ.
Вернёмся к 3 закону Ньютона . Два тела сталкиваясь, действуют друг на друга силами F12 F21 отсюда 𝑚1⃗а⃗1 = 𝑚2⃗а⃗2 илиm1Δυ1m2Δυ2 , откуда
![]() υ
υ
m1 1 m2υ2 m m2υ12
в замкнутой системе сумма импульсов тел до взаимодействия равна сумме
импульсов тел после взаимодействия.
Это закон сохранения импульсов тел. Произведение массы на скорость тела называется количеством движения или импульсом тела ⃗р⃗ и измеряется в килограмм-метрах в секунду (кг•м/с).
В замкнутой системе сумма импульсов тел - величина постоянная.
![]() . Если за m2 принять
эталонную массу, то
. Если за m2 принять
эталонную массу, то
определённая таким способом масса называется инертной и характеризует способность тела сохранять свою скорость. Инертная масса – физическая величина, характеризующая инертность тел.
Пример1: Вагон массой 20 т, движущийся со скоростью 0,3 м /с, нагоняет вагон массой 30 т, движущийся со скорость 0,2 м /с, после упругого столкновения второй вагон стал двигаться со скоростью 0,25 м /с. Определить скорость первого вагона?
![]() Дано: Записываем закон сохранения m1=20т
импульса в векторной форме: υ1=0,3м/с m1υ1 m2υ2 m1υ11 m2υ12 m2=30т
спроектируем вектора на ось ОХ υ2=0,2м/с m1υ1х +
m2υ2х = m1υ1х| + m2
υ2х|
Дано: Записываем закон сохранения m1=20т
импульса в векторной форме: υ1=0,3м/с m1υ1 m2υ2 m1υ11 m2υ12 m2=30т
спроектируем вектора на ось ОХ υ2=0,2м/с m1υ1х +
m2υ2х = m1υ1х| + m2
υ2х|
υ2|=0,25м/с m
m2υ2x m2υ12x = υ1|=?
υ11 ![]() 1υ1x
1υ1x
m1
![]()
=0,225м/с
Ответ: после столкновения первый вагон будет двигаться со скоростью 0,225м/с знак “ + “ говорит о том, что скорость υ1| направлена вдоль оси ОХ.
Пример 2. С судна массой 600т произведен выстрел из пушки под углом 60o к горизонту. Какова стала скорость судна, если оно не двигалось? Скорость снаряда 1000 м /с, а его масса 50 кг.
![]() Дано:
Запишем закон сохранения импульса m1 = 600 m1υ1 m2υ2 m1υ11 m2υ12 υ1 = 0
Дано:
Запишем закон сохранения импульса m1 = 600 m1υ1 m2υ2 m1υ11 m2υ12 υ1 = 0
m2 = 50 кг Рассмотрим движение судна вдоль оси υ2 = 0 Х. Систему можно считать замкнутой υ1 = ? только в начальный момент времени.
Спроектируем импульсы на ось ОХ.
О + О = m1υ1| + m2υ2|cosφ
![]()
![]() υ11
m2υ2 cos
5010000,5
0,042м/с
m1 600000
υ11
m2υ2 cos
5010000,5
0,042м/с
m1 600000
Знак “ - “ говорит о том, что υ1| направлена против оси ОХ Ответ: после выстрела корабль приобретёт скорость 0,042м/с.
Пример 3. Вагон массой 10 т двигается со скоростью 0,1 м/с. Навстречу ему двигается вагон массой 30т со скоростью 0,5 м/с. Определить скорость вагонов после срабатывания автосцепки.
![]()
![]() Дано: Записываем закон сохранения импульса m1 = 10 т m1υ1
m2υ2 m1υ11 m2υ12 υ1 = 0,1 м /с спроектируем на
ось ОХ; m2 = 30 т m1υ1 - m2υ2 = (
m1 + m2)υ υυ2 == ? 0.5 м
/с υ m1υ1
m2υ2
Дано: Записываем закон сохранения импульса m1 = 10 т m1υ1
m2υ2 m1υ11 m2υ12 υ1 = 0,1 м /с спроектируем на
ось ОХ; m2 = 30 т m1υ1 - m2υ2 = (
m1 + m2)υ υυ2 == ? 0.5 м
/с υ m1υ1
m2υ2
m1 m2
υ
![]()
0,35м/с
0,35м/с
Ответ: после срабатывания автосцепки скорость вагонов будет равна 0,35м/с и направлена против оси х.
Но вернемся к закону сохранения импульса в виде m1Δυ1 m2Δυ2
разделим обе части равенства на время воздействия, ведь оно у тел одно и тоже.
![]()
![]() m1Δυ1
m2Δυ2 , а это сила
поэтому - это вторая запись второго закона t t ∆𝐭
m1Δυ1
m2Δυ2 , а это сила
поэтому - это вторая запись второго закона t t ∆𝐭
Ньютона, или ![]() , или 𝐹⃗ = ⃗𝑝⃗⃗⃗|. Сила, действующая на
тело равна первой производной импульса тела по времени.
, или 𝐹⃗ = ⃗𝑝⃗⃗⃗|. Сила, действующая на
тело равна первой производной импульса тела по времени.
![]() Но вернёмся к Fma
Fmυυo Ft
mυ-mυo Ft
p
t
Но вернёмся к Fma
Fmυυo Ft
mυ-mυo Ft
p
t
Это запись закона сохранения импульса для не замкнутой системы. Импульс внешней силы (Ft) равен изменению количества движения ∆(mυ) или изменению импульса тела.
Ft - называется импульсом силы и измеряется в ньютон-секундах (Н•с). Импульс силы равен изменению импульса тела.
ЗАДАЧИ
1. Движение материальной точки описывается уравнением х = 2 – 3t + t2. Приняв ее массу равной 4 кг, найти импульс через 2 с и через 5 с после начала отсчета времени.
2. Материальная точка массой 2 кг равномерно движется по окружности со скоростью 8 м/с. Найти изменение импульса за одну четверть периода; период.
3. С какой скоростью должна лететь хоккейная шайба массой 100 г, чтобы ее импульс был равен импульсу пули массой 8 г, летящей со скоростью 400 м/с.
4. Снаряд массой 15 кг, летящий горизонтально со скоростью 400 м/с, попадает в платформу с песком массой 10 т и застревает в песке. С какой скоростью стала двигаться платформа?
5. Охотник стреляет из ружья с движущейся лодки по направлению ее движения. Какую скорость имела лодка, если она остановилась после четырех, быстро следующих друг за другом выстрелов? Масса охотника с лодкой 90 кг, масса заряда 20 г средняя скорость дроби и пороховых газов 500 м/с.
ВОПРОСЫ:
1. Что называется импульсом тела?
2. Сформулируйте закон сохранения импульса для замкнутой системы.
3. Что называется инертной массой?
4. Что называется импульсом силы?
5. Сформулируйте закон сохранения импульса для не замкнутой системы.
6. Запишите второй закон Ньютона через изменение импульса 7. Как называется масса, измеренная при помощи столкновения тел?
8. Как называется масса, измеренная взвешиванием?
9. Что называется инертностью?
10. Сформулируйте закон сохранения импульса для незамкнутой системы
ДОМАШНЕЕ ЗАДАНИЕ 14
1. Движение материальной точки описывается уравнением х = 1 – 3t + 6t2. Приняв ее массу равной 3 кг, найти импульс через 2 с и через 8 с после начала отсчета времени.
2. Материальная точка массой 3 кг равномерно движется по окружности со скоростью 12 м/с. Найти изменение импульса за одну четверть периода; период.
3.
![]() С какой скоростью должна лететь хоккейная шайба массой 200
г, чтобы ее импульс был равен импульсу пули массой 8 г, летящей со скоростью
700 м/с.
С какой скоростью должна лететь хоккейная шайба массой 200
г, чтобы ее импульс был равен импульсу пули массой 8 г, летящей со скоростью
700 м/с.
4. Снаряд массой 25 кг, летящий горизонтально со скоростью 700 м/с, попадает в платформу с песком массой 12 т и застревает в песке. С какой скоростью стала двигаться платформа?
7. Охотник стреляет из ружья с движущейся лодки по направлению ее движения. Какую скорость имела лодка, если она остановилась после пяти, быстро следующих друг за другом выстрелов? Масса охотника с лодкой 120 кг, масса заряда 20 г средняя скорость дроби и пороховых газов 500 м/с.
8. Молекула массой 5 1026 кг, летящая со скоростью 500 м/с, упруго ударяется о стенку под углом 30° к перпендикуляру. Найти импульс силы, полученный стенкой при ударе.
4,35 10-23 Нс
16. РЕАКТИВНОЕ ДВИЖЕНИЕ. УРАВНЕНИЕ МЕЩЕРСКОГО.
ФОРМУЛА ЦИОЛКОВСКОГО.
Практическим применением закона сохранения импульса является реактивное движение. Так называют движение, которое возникает, когда от тела отделяется и движется с некоторой скоростью какая-то его часть. Например, пушка стреляет в одну сторону, судно двигается в другую (явление отдачи). В ракете продукты горения (газ) с большой скоростью движутся в одну сторону, а ракета в другую.
Пусть в момент времени to = 0 ракета массой m двигалась со скоростью υо. За малый промежуток времени ∆t из ракеты выбрасывается масса газа ∆m со скоростью и относительно ракеты, т.е. со скоростью V1=и + υ относительно Земли. По закону сохранения
импульса имеем mυo (mΔm)υΔmV1 . Подставив значения V1=и + υ и υ=υо +∆υ,
получим: mΔυΔmи . Разделим обе части уравнения на ∆t и вспомнив, что ∆υ/∆t=a -
ускорение, а ∆m /∆t = μ – ежесекундный расход топлива получим maμи . Это реактивная сила тяги. Тогда для движения тела с переменной массой второй закон Ньютона
![]() запишется
так: ma
FFр1 Fр2, где F – главный вектор всех сил,
действующих на тело (равнодействующая всех сил) Fр1 - реактивная
сила тяги присоединяющейся массы, Fр2 - реактивная сила тяги
отделяющейся массы. Это уравнение называется уравнением МЕЩЕРСКОГО. При
отсутствии внешнего воздействия F=0, а для ракетного двигателя сила со стороны
поступающего воздуха Fр1=0. Получим maμиили
m dυ и dm . Разделим
запишется
так: ma
FFр1 Fр2, где F – главный вектор всех сил,
действующих на тело (равнодействующая всех сил) Fр1 - реактивная
сила тяги присоединяющейся массы, Fр2 - реактивная сила тяги
отделяющейся массы. Это уравнение называется уравнением МЕЩЕРСКОГО. При
отсутствии внешнего воздействия F=0, а для ракетного двигателя сила со стороны
поступающего воздуха Fр1=0. Получим maμиили
m dυ и dm . Разделим
dt dt
dυ dm υ dυ m dm
![]()
![]()
|
М eиυ m |
|
до υ, а масса ракеты изменяется от М до m. Если скорость истечения газа и постоянна то υ 0 υ М
![]()
![]() получим lnm
lnМ или
ln
или . Эта формула называется u u u m
получим lnm
lnМ или
ln
или . Эта формула называется u u u m
формулой Циолковского. Cкорость ракеты можно вычислить из уравнения Циолковского
М υ υo uln ![]() .
.
m
ЗАДАЧИ:
1. Чему равен ежесекундный расход топлива в момент старта ракеты массой 10т, если она стартует вертикально с ускорением 4м/с2. Скорость истечения газов относительно ракеты 5000м/с.
2. Определите ускорение ракеты массой 105кг через 2мин после старта при ежесекундном расходе топлива μ = 6•103кг/с. Скорость истечения газов относительно ракеты постоянна и равна 3•103м/с. Ракета движется вертикально вверх.
3. Масса ракеты с топливом М = 106кг. Рассчитайте расход топлива, необходимый для достижения первой космической скорости 8 км/с, если скорость газовой струи относительно ракеты равна 8•103 кг/с.
4. Масса с топливом 300т. Определить полезную массу ракеты, если ракета достигла скорости 13 м/с. Скорость истечения газов 6•103м/с. Без учёта влияния силы тяжести.
Вопросы:
1. Какое движение называется реактивным?
2. Приведите примеры реактивного движения в технике.
3. Приведите примеры реактивного движения в природе.
4. Как вычислить реактивную силу тяги?
5. Запишите уравнение Мещерского.
6. Запишите формулу Циолковского.
ДОМАШНЕЕ ЗАДАНИЕ 15
1. Чему равен ежесекундный расход топлива в момент старта ракеты массой 106 кг, если она стартует вертикально с ускорением 3м/с2. Скорость истечения газов относительно ракеты 4000м/с.
Отв: 3,25•103 кг/с.
2. Чему равен ежесекундный расход топлива в момент старта ракеты массой 10т, если она стартует вертикально с ускорением 1м/с2. Скорость истечения газов относительно ракеты 5000м/с.
3. Определите ускорение ракеты массой 106кг через 1мин после старта при ежесекундном расходе топлива μ = 7,5•103кг/с. Скорость истечения газов относительно ракеты постоянна и равна 2•103м/с. Ракета движется вертикально вверх.
Отв:17,3 м/с2.
4. ![]() Масса ракеты
с топливом М = 106кг. Рассчитайте расход топлива, необходимый для
достижения первой космической скорости 8 км/с, если скорость газовой струи
относительно ракеты равна 4•103 кг/с.
Масса ракеты
с топливом М = 106кг. Рассчитайте расход топлива, необходимый для
достижения первой космической скорости 8 км/с, если скорость газовой струи
относительно ракеты равна 4•103 кг/с.
Отв: 8,65•105 кг.
5. Масса с топливом 200т. Определить полезную массу ракеты, если ракета достигла скорости 8 м/с. Скорость истечения газов 5•103м/с. Без учёта влияния силы тяжести.
17. ЭНЕРГИЯ. МЕХАНИЧЕСКАЯ РАБОТА И МОЩНОСТЬ.
Энергия
Ещё одна важнейшая характеристика состояния материи - энергия. Энергия (др.-греч. ἐνέργεια — «действие, деятельность, сила, мощь») — скалярная физическая величина, являющаяся единой мерой различных форм движения и взаимодействия материи, мерой перехода движения материи из одних форм в другие. Введение понятия энергии удобно тем, что в случае, если физическая система является замкнутой, то её энергия сохраняется в этой системе на протяжении времени, в которое система будет являться замкнутой. Это утверждение носит название закона сохранения энергии. Понятие введено Аристотелем в трактате «Физика». Существует несколько видов энергии: механическая, внутренняя, энергия электромагнитного взаимодействия, ядерная энергия и т.д.
Один вид энергии может преобразовываться в другой, например энергия электрического тока может преобразовываться в энергию движения в электродвигателе. Сама по себе энергия определяет состояние системы тел и нам особо ничего не даёт, а вот изменение энергии даёт нам работу.
Работа является мерой изменения энергии.
Работа
Обиходное представление о работе это перемещение тел под действием силы. Перемещение грузов, вскапывание земли, забивание гвоздей и т.д. В физике под работой понимается скалярное произведение вектора силы и вектора перемещения.
А = (𝐹⃗ ∙ 𝑆⃗ ) или А = 〈𝐹⃗ ∙ 𝑆⃗〉
Скалярное произведение двух векторов равно произведению модулей векторов на косинус угла между ними.
В общем случае А = |⃗𝑭⃗⃗| · |𝑺⃗⃗| · 𝐜𝐨𝐬 𝝋- для постоянной силы.
Пусть человек равномерно поднимает груз на высоту Н, при равномерном движении равнодействующая всех сил равна нулю. На груз действуют сила тяжести со стороны Земли и сила тяги со стороны человека. Запишем II закон Ньютона для, поднимаемого тела.
![]() FT Fтяги ma . В
проекциях на ось ОY получим: Fтяги-Fт=0, или Fтяги=Fт,
умножим обе части формулы на высоту Н, получим FтягихН=FтхН,
Н- это путь FтягихS=FтхS. Работа одной силы (ускоряющей)
равна работе другой силы (тормозящей). При равномерном движении сумма работ
всех сил равна нулю. Работа измеряется в джоулях (Дж).
FT Fтяги ma . В
проекциях на ось ОY получим: Fтяги-Fт=0, или Fтяги=Fт,
умножим обе части формулы на высоту Н, получим FтягихН=FтхН,
Н- это путь FтягихS=FтхS. Работа одной силы (ускоряющей)
равна работе другой силы (тормозящей). При равномерном движении сумма работ
всех сил равна нулю. Работа измеряется в джоулях (Дж).
Итак, при равномерном движении работа одних сил равна работе других сил.
А1=А2
При равномерном движении автомобиля работа двигателя (работа силы тяги) равна работе сил трения и сопротивления.
![]() Работу можно
вычислить графически, если на оси ОУ откладывать значения силы, а на оси ОХ
перемещение, то площадь фигуры под графиком будет числено равна
Работу можно
вычислить графически, если на оси ОУ откладывать значения силы, а на оси ОХ
перемещение, то площадь фигуры под графиком будет числено равна
А = FS, если сила является переменной, то работа всё равно численно равна площади под графиком зависимости силы от перемещения.
Пример: Какую работу совершает сила тяжести, действующая на дождевую каплю массой 20мг, при её падении с высоты 2км?
![]() Дано: Работу найдём
по формуле А=Fscosα. Угол α между m =20x10- вектором силы
и вектором перемещения равен нулю. Отсюда
Дано: Работу найдём
по формуле А=Fscosα. Угол α между m =20x10- вектором силы
и вектором перемещения равен нулю. Отсюда
6кг A=FS
Н = 2х103 Сила тяжести равна FТ=mG или FT=mg. Перемещение
м это Н
А = ? А=mgН, А=2х10-7х9,8х2х103=40х10-4Дж
Ответ: Сила тяжести совершает работу по перемещению капельки равную 4х10-3Дж.
Пример: Какую работу совершает человек при подъёме груза массой 2кг на высоту 1м с ускорением 3м/с?
![]() Дано: Запишем закон II
Ньютона. Fma
F FТЯГИ FT . В m = 2 кг проекциях
FТЯГИ-FT=ma, откуда FТЯГИ=m(a+g). Работу
Дано: Запишем закон II
Ньютона. Fma
F FТЯГИ FT . В m = 2 кг проекциях
FТЯГИ-FT=ma, откуда FТЯГИ=m(a+g). Работу
H = 1 м 2 перемещением и силой тяги) FТЯГИScosS=H, отсюда А=. =0 (угол между m(a+g)S найдём по формуле А=
а = 3 м/с
А =? A=2x(3+9,8)x1=26 Дж
Ответ: Человек совершает работу в 26 Дж.
Работа, произведённая в единицу времени называется мощностью. Обозначается N и
A
измеряется в
ваттах (Вт). N ![]() . Если представить работу как силу
умноженную на t
. Если представить работу как силу
умноженную на t
перемещение, то получим NFυ . Из этой формулы следует, что при постоянной мощности двигателя автомобиля для увеличения силы тяги, например на подъёме, необходимо уменьшить скорость с помощью переключения на пониженную передачу и наоборот.
18. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Пусть тело движется по горизонтальной поверхности под действием силы тяги. Сила
2 2
υ υo , трения равна нулю,
тогда работа силы тяги A=Fтяги S, (cosφ=1, т.к.φ=0). Fтяги=ma,
S ![]()
2a
2 2
|
2 2 |
![]() υ
υo
отсюда A ma
, или
υ
υo
отсюда A ma
, или
2a
𝑚𝜐2 ![]() назовём кинетической энергией тела.
назовём кинетической энергией тела.
2
Работа силы (или равнодействующей сил) равна изменению кинетической энергии тела. Это утверждение называется теоремой о кинетической энергии.
Работа является мерой изменения энергии.
Пример: Какую работу нужно совершить для увеличения скорости поезда υ1=72км/час, до скорости υ2=108км/час? Масса поезда 1000т. Какова должна быть сила тяги локомотива, если это увеличение должно произойти на участке длиной 2000м?
![]() Дано:
Для определения работы используем
Дано:
Для определения работы используем
![]() υо=72км/час
- A
mυ2 mυo2
103 302 103 202
υо=72км/час
- A
mυ2 mυo2
103 302 103 202
20м/с формулу 2 2 2
υ=108км/час-30 =2,5х108Дж Если A=FS, то F=A/S
м/с F=2,5х108/2000=1,25х105Н
m=1000т - Ответ: При увеличении скорости поезда, 103кг совершается работа 2,5х108Дж и развивается
|
S=2000м А=? Fтяги=?
|
тяговое усилие 125кН.
|
Работу можно производить медленно или быстро. Быстрота
производимой работы называется мощностью. ![]() и измеряется в Ваттах
(Вт). При равномерном движении имеем:
и измеряется в Ваттах
(Вт). При равномерном движении имеем: ![]() . При постоянной
мощности можно увеличить силу тяги за счёт
. При постоянной
мощности можно увеличить силу тяги за счёт
уменьшения скорости (пониженная передача) на подъёме Или наоборот увеличить скорость на ровном участке шоссе, но при этом уменьшится сила тяги.
Вопросы :
1. Что такое энергия?
2. Какие виды энергии вы знаете?
3. Что является мерой изменения энергии?
4. Что такое работа?
5. Чему равно скалярное произведение двух векторов?
6. Как графически определить работу?
7. Что называется мощностью?
8. По какой формуле вычисляется мощность?
9. Что называется кинетической энергией тела?
10. О чём гласит теорема о кинетической энергии?
ДОМАШНЕЕ ЗАДАНИЕ 16
1. Какую работу нужно совершить для увеличения скорости поезда υ1=54км/час, до скорости υ2=72км/час? Масса поезда 1500т. Какова должна быть сила тяги локомотива, если это увеличение должно произойти на участке длиной 2000м?
2. Сплавщик передвигает багром плот, прилагая к багру силу 200 Н. Какую работу совершит сплавщик, переместив плот на 10 м, если угол между направлением силы и направлением перемещения 45° ?
1,4 кДж
3. При равномерном спуске груза по наклонному настилу тормозящая сила 1 кН направлена под углом 150° к направлению движения груза. Определите работу тормозящей силы, если длина настила 5 м.
-4,3 кДж
4. Сила тяги сверхзвукового самолета при скорости полета 2340 км/ч равна 220 кН. Найти мощность двигателей самолета в этом режиме полета.
143 МВт
4. Мощность электровоза равна 4000 кВт. Найдите силу тяги электровоза при скорости движения 72 км/ч.
200 кН
![]()
19. ВЕКТОРНЫЕ ПОЛЯ.
Существует четыре фундаментальных взаимодействия: гравитационное, электромагнитное, сильное и слабое. Вся совокупность элементарных частиц с их взаимодействиями проявляет себя в форме вещества и поля. Поле в отличие от вещества обладает особыми свойствами. Оно распределено в пространстве и передаёт взаимодействие.
Электромагнитное поле может существовать самостоятельно, например свет, радиоволны.
![]() Они имеют конечную скорость распространения.
Они имеют конечную скорость распространения.
Гравитационное поле реально ощутимо вокруг массивных тел. Источником электромагнитного поля являются движущиеся заряженные частицы. Взаимодействие зарядов происходит по схеме частица – поле – частица. Схема гравитационного взаимодействия, вероятно, такая же. В некоторых условиях поле может оторваться от источника и свободно распространяться в пространстве. Такое поле носит волновой характер.
Состояние материальной точки задавалось её положением в пространстве и её скоростью. Такой способ описания непригоден для полей. Основное свойство полей - передача взаимодействия (силы). Поле определено, если для каждой точки пространства известны значения вектора напряжённости. Напряжённость поля – вектор численно равный силе действующей на тело, обладающего единицей величины, характеризующей данное взаимодействие. Линии, в каждой точке которой вектор напряжённости является касательным, называются силовыми линиями или линиями вектора напряжённости.
Для описания векторных полей очень удобным оказываются понятия потока и циркуляции поля.
Элементарный поток векторного поля ⃗В⃗⃗⃗ через поверхность ΔS равен
![]() ΔФ=В𝑛 ∙ ∆𝑆
, где ΔФ – элементарный поток вектора ⃗В⃗⃗,
Вn – проекция вектора ⃗В⃗⃗
на нормаль к поверхности, ΔS – элементарная поверхность. Для того, что бы
вычислить полный поток вектора ⃗В⃗⃗
через поверхность необходимо сложить элементарные потоки.
ΔФ=В𝑛 ∙ ∆𝑆
, где ΔФ – элементарный поток вектора ⃗В⃗⃗,
Вn – проекция вектора ⃗В⃗⃗
на нормаль к поверхности, ΔS – элементарная поверхность. Для того, что бы
вычислить полный поток вектора ⃗В⃗⃗
через поверхность необходимо сложить элементарные потоки.
![]() =
=
(Bn)1∙ΔS1+(Bn)2∙ΔS2+(Bn)3∙ΔS3+(Bn)4∙ΔS4+(Bn)5∙ΔS5+
….+(Bn)n∙ΔSn
В короткой записи это выглядит так: Ф = ∫ 𝐵𝑛 ∙ 𝑑𝑆
![]()
Элементарная циркуляция векторного поля ⃗В⃗⃗ вдоль замкнутого контура равна
ΔГ=Вτ·Δℓ, где ΔГ – элементарная циркуляция вектора ⃗В⃗⃗,
Вτ – проекция вектора ⃗В⃗⃗ на касательную к точке контура, Δℓ
- длина элементарного участка контура. Полную циркуляцию по замкнутому контуру можно вычислить, если
сложить элементарные циркуляции.
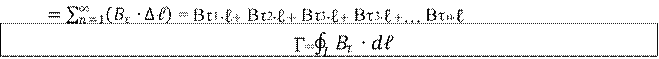 Г или
Г или
ВОПРОСЫ:
1. Какие фундаментальные взаимодействия вы знаете?
2. Какие функции выполняют поля?
3. Что называется напряжённостью поля?
4. Что называется линиями напряжённости поля?
5. Что называется элементарным потоком векторного поля ⃗В⃗⃗⃗ через поверхность ΔS?
6. Что называется элементарной циркуляцией вектора напряжённости вдоль замкнутого контура?
20. ЛАМИНАРНОЕ ТЕЧЕНИЕ ЖИДКОСТИ
![]() Движение
жидкости и газа описывается векторным полем скоростей. Рассмотрим движение воды
в ручье. Движение спокойное без водоворотов (ламинарное). У ручья есть исток и
сток. Если для каждой точечной массы воды изобразить вектор скорости, то
совокупность этих векторов будет являться векторным полем - полем скоростей.
Траектории движения частиц - создадут линии тока.
Движение
жидкости и газа описывается векторным полем скоростей. Рассмотрим движение воды
в ручье. Движение спокойное без водоворотов (ламинарное). У ручья есть исток и
сток. Если для каждой точечной массы воды изобразить вектор скорости, то
совокупность этих векторов будет являться векторным полем - полем скоростей.
Траектории движения частиц - создадут линии тока.
В каждой точке линии тока скорость является касательной. Поверхность, образованная линиями тока, проведёнными через все точки малого замкнутого контура, называется трубкой тока. Часть жидкости или газа, заключённая в трубке тока называется струйкой.
Движение жидкости называется установившемся или стационарным, если поле её скоростей не изменяется.
Пусть за одну секунду через поперечное сечение S1 проходит количество воды объёмом Ф=V/t. Ф – поток жидкости или объёмный расход.
![]() .
.
Поток вектора скорости через поверхность S равен Ф=υScosα, где α – угол между вектором скорости и нормалью (перпендикуляр) к поверхности. Пусть каждая частица,
поглощаясь
поверхностью S1 действует на неё с силой ![]() или
или ![]() . Найдём силу, действующую со стороны всех частиц. Для этого
необходимо умножить обе части уравнения на число частиц, падающих на
площадку.
. Найдём силу, действующую со стороны всех частиц. Для этого
необходимо умножить обе части уравнения на число частиц, падающих на
площадку. ![]() или
или ![]() ⃗ ⃗ ⃗.
⃗ ⃗ ⃗.
![]() 𝑣
𝑣
– средняя
скорость, которая равна ![]() .
.
2
Найдём давление, производимое на поверхность. Для этого разделим обе части уравнения на площадь S1.
Тогда
получим  . За промежуток времени t значение скорости меняется от υ до 0.
Δυ = υ.
. За промежуток времени t значение скорости меняется от υ до 0.
Δυ = υ.
![]()
Давление, производимое на поверхность, перпендикулярную скорости равно плотности кинетической энергии. Это давление называется динамическим или скоростным напором.
Поток жидкости имеет начало – исток, и конец – сток. Заметим, что линии тока выходят из истока, а входят в сток.
ВОПРОСЫ:
1. Что такое «линии тока»?
2. Что называется трубкой тока?
3. Что называется струйкой?
4. Что называется потоком жидкости через поперечное сечение?
5. Чему равен скоростной напор?
21. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОСТИ. ВИХРЕВОЕ ПОЛЕ.
![]()
Турбулентное течение - форма течения жидкости или газа, при которой вследствие наличия в течении многочисленных вихрей различных размеров жидкие частицы совершают хаотическое неустановившиеся движения по сложным траекториям. Рассмотрим вихревое поле скоростей. Примером вихревого поля скоростей может служить водный водоворот в ванне, когда мы начинаем спускать воду, воздушные вихри-смерчи. Идеальное вихревое поле – поле линии напряжённости которого являются замкнутыми. Элементарная циркуляция вектора скорости частиц воды по участку контура ℓ равна ΔГ = υτ·Δℓ, если в качестве контура взять окружность, то из соображений симметрии, значение скорости в каждой точке будет одинаково по модулю и скорость тела будет являться касательной к каждой точке окружности. Тогда циркуляция вектора скорости равна
Г=υ·2πr , откуда
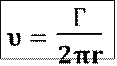
ВОПРОСЫ:
1. Что называется элементарной циркуляцией вектора напряжённости вдоль замкнутого контура?
2. Что называется вихревым полем?
3. Как определить скорость воды в любо точке?
Задачи
1. Определить объёмный расход воды, движущейся со скоростью 50см/с по трубе диаметром 200мм. Скорость считать одинаковой по всему сечению
2. Ежесекундный расход 2л/с. Определить диаметр трубы, если скорость движения воды 1500мм/мин. Скорость считать одинаковой по всему сечению.
3. Определить скоростной напор в трубе диаметром 500мм, если скорость движения жидкости 30000 мм/мин. (Скоростной напор является давлением, выраженным в единицах
![]() 2
2
длины
4. На расстоянии 0,02км от центра смерча скорость воздуха составляет 36км/час. Определить циркуляцию вектора скорости. Определить скорость на расстоянии 0,1км от центра смерча.
5. Скорость воды на расстоянии 100 мм от сливного отверстия 20см/с. Определить циркуляцию вектора скорости, а также скорость воды на расстоянии 250 мм от сливного отверстия.
ДОМАШНЕЕ ЗАДАНИЕ 16
1. Определить объёмный расход воды, движущейся со скоростью 25 см/с по трубе диаметром 100мм. Скорость считать одинаковой по всему сечению
2. Ежесекундный расход 1л/с. Определить диаметр трубы, если скорость движения воды 1200 мм/мин. Скорость считать одинаковой по всему сечению.
3. Определить скоростной напор в трубе диаметром 200 мм, если скорость движения жидкости 10000 мм/мин. (Скоростной напор является давлением, выраженным в единицах
![]() 2
2
длины .
4. На расстоянии 0,03км от центра смерча скорость воздуха составляет 72км/час. Определить циркуляцию вектора скорости. Определить скорость на расстоянии 0,1км от центра смерча.
5. Скорость воды на расстоянии 10 мм от сливного отверстия 10 см/с. Определить циркуляцию вектора скорости, а также скорость воды на расстоянии 100 мм от сливного отверстия.
Гравитационное поле – особый вид материи, передающий гравитационное взаимодействие. Это пространство вокруг массивных тел. Примером гравитационного взаимодействия является взаимодействие между Землёй и Луной, Солнцем и планетами, и т.д. Частный случай гравитационного взаимодействия – сила тяжести. Внесём в гравитационное поле Земли небольшое тело. В данной точке отношение силы тяжести к массе тела величина постоянная и зависит только от массы Земли. Для гравитационного поля напряжённость поля равна
![]()
![]()
Для изображения полей используют линии напряжённости. Линии напряжённости это линии в каждой точке которой вектор напряжённости является касательным. Напряжённость – как скорость в потоке воды, а линии напряжённости – линии тока.
Для описания полей используют понятия поток поля и циркуляция поля.
![]()
![]() Элементарный
поток векторного поля равен произведению нормальной составляющей вектора на
площадь поверхности, которую он пронизывает.
Элементарный
поток векторного поля равен произведению нормальной составляющей вектора на
площадь поверхности, которую он пронизывает.
𝜟Ф=Вn·𝜟S или dФ=В·dS·cos(𝐵⃗⃗,𝑛⃗⃗). Для вычисления полного потока через некоторую поверхность необходимо проинтегрировать данное выражение.
Представим сферу вокруг Земли. Поток напряжённости пронизывает сферу. Полный поток напряжённости
гравитационного поля Земли равен
Ф=GS,
где S – площадь сферы, G- напряжённость гравитационного поля Земли.
Поток напряжённости гравитационного поля Земли пропорционален источнику поля, т.е. массе Земли М. Ф = кМ.
![]()
![]() Отсюда
GS = кМ, откуда напряжённость гравитационного, поля кM образованного
Землёй, или другим сферическим телом равна или
Отсюда
GS = кМ, откуда напряжённость гравитационного, поля кM образованного
Землёй, или другим сферическим телом равна или
![]()
![]() ,
,
где γ – гравитационная постоянная
Найдём силу, действующую на тело массой m.
![]() ,
,
Эта формула выражает закон всемирного тяготения.
Два сферических или точечных тела притягиваются с силой прямо пропорциональной произведению масс и обратно пропорциональной квадрату расстояния между их центрами.
γ = ( 6,670 ± 0,006 )х10-11Н м / кг
Вблизи поверхности Земли ускорение, с которым движутся тела, можно считать постоянным и оно называется ускорением свободного падения 𝑔⃗ . Силу можно вычислить по второму закону Ньютона. F=mg. Эта сила называется силой тяжести, но F=Gm отсюда ⃗𝑮⃗⃗ = ⃗𝒈⃗⃗. Напряжённость гравитационного поля равна ускорению свободного падения.
Массу определяют взвешиванием.
![]() , где Fт – сила тяжести.
, где Fт – сила тяжести.
Первоначально (XVII—XIX века) масса характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться изменению скорости от приложенной силы (инертность), так и гравитационные свойства — вес.
В современной физике понятие «количество вещества» имеет другой смысл, а концепцию «массы» можно трактовать несколькими способами:
• Пассивная гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями — фактически эта масса положена в основу измерения массы взвешиванием в современной метрологии.
• Активная гравитационная масса показывает, какое гравитационное поле создаёт само это тело — гравитационные массы фигурируют в законе всемирного тяготения.
• Инертная масса характеризует инертность тел и фигурирует в одной из формулировок второго закона Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные исходно неподвижные тела, этим телам приписывают одинаковую инертную массу.
![]() Гравитационные
и инертная масса равны друг другу (с высокой точностью — порядка 10−13
— экспериментально, а в большинстве физических теорий, в том числе всех,
подтверждённых экспериментально — точно), поэтому в том случае, когда речь идёт
не о «новой физике», просто говорят о массе,
не уточняя, какую из них имеют в виду. Масса при скоростях много меньших
скорости (классическая механика) света является постоянной, а при скоростях
близких к скорости света зависит от скорости движения тела (релятивистская
механика).
Гравитационные
и инертная масса равны друг другу (с высокой точностью — порядка 10−13
— экспериментально, а в большинстве физических теорий, в том числе всех,
подтверждённых экспериментально — точно), поэтому в том случае, когда речь идёт
не о «новой физике», просто говорят о массе,
не уточняя, какую из них имеют в виду. Масса при скоростях много меньших
скорости (классическая механика) света является постоянной, а при скоростях
близких к скорости света зависит от скорости движения тела (релятивистская
механика).
ВОПРОСЫ:
1. Что называется гравитационным полем?
2. Чему равна напряжённость гравитационного поля по определению?
3. Чему равна напряжённость гравитационного поля сферического тела?
4. Как связаны напряжённость гравитационного поля и ускорение свободного падения?
5. Сформулируйте закон всемирного тяготения.
6. Что называется инертной массой?
7. Что называется гравитационной массой?
ЗАДАЧИ:
1. Расстояние между центрами двух шаров 1 м, масса каждого – 1 кг. Определить сила тяготения между ними.
2. Космонавт, находясь на Земле, притягивается к ней с силой 700 Н, с какой силой он будет притягиваться к Марсу, находясь на его поверхности. Радиус Марса в 2 раза, а масса – в 10 раз меньше, чем у Земли.
3. Искусственный спутник обращается по круговой орбите на высоте 600 км от поверхности планеты. Радиус планеты равен 3400 км, ускорение свободного падения равно 4 м/с2. Какова скорость движения спутника по орбите?
ДОМАШНЕЕ ЗАДАНИЕ 18
1. На каком расстоянии находятся два тела массой 15т, если сила гравитационного взаимодействия между ними равна 1,5 ·10-20 Н
2. Искусственный спутник обращается по круговой орбите на высоте 600 км от поверхности планеты со скоростью 3,4 км/с. Радиус планеты 3400 км. Чему примерно равно ускорение свободного падения на поверхности планеты?
3. Подлетев к неизвестной планете, космонавты придали своему кораблю горизонтальную скорость 11 км/с. Эта скорость обеспечила полет корабля по круговой орбите радиусом 9100 км. Каково ускорение свободного падения у поверхности плац ты, если ее радиус 8900 км? 14 м/с2
5. Определить минимальный период обращения спутника нейтронной звезды, плотность вещества которой 1017 кг/м3.
1,210-3 с
![]()
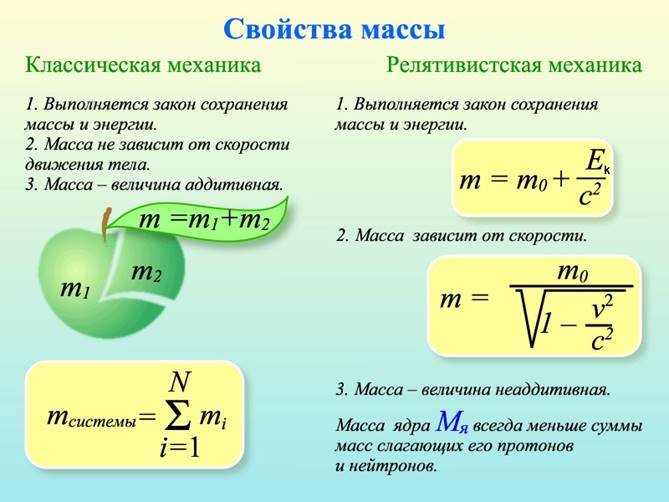
23. СТРОЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ.
Сегодня большинство исследователей считает, что Солнце, подобно другим звёздам, возникло в результате конденсации материи в центральной части огромного роя холодной пыли и газа под действием гравитационных сил.
При загорании звезды, часть вещества, выброшенная из центра, образовала планеты. Может быть, согласно другой теории, Солнце захватило такое облако. И в том и в другом случае под действием сил тяготения Солнца первоначально бесформенный рой межзвёздного вещества сгустился и превратился во вращающееся облако мелких твёрдых частиц и газа. Лёгкие частицы выносились «солнечным ветром» в среднюю часть облака, а тяжёлые и тугоплавкие остались вблизи Солнца.
Частицы вещества, вращаясь вокруг Солнца, сталкивались, объединялись и образовали планеты.
Вблизи от Солнца формировались небольшие (не хватило вещества), но плотные планеты. В средней части протопланетного диска (облака) выросли планеты с меньшей плотностью, но большой массой, с большим содержанием водорода, гелия, аммиака, углекислого газа, метана.
Вокруг Солнца вращаются девять планет: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон. По физическим характеристикам их объединяют в две группы, разграниченные поясом астероидов ( малых планет).
Планеты земной группы (Меркурий, Венера, Земля, Марс) находятся внутри пояса астероидов. Планеты небольшие, имеют плотность близкую к плотности Земли и обладают атмосферами (кроме Меркурия). Земля и Марс имеют спутники.
Планеты, движущиеся за кольцом астероидов, образуют группу планет-гигантов:
Юпитер, Сатурн, Уран, Нептун. Плутон мало изучен и не отнесён ни к одной из групп (Плутон является двойной планетой как Земля). Планеты-гиганты обладают значительными размерами и массами, малой средней плотностью, быстрым вращением, гелиевоводородными, с содержанием аммиака и метана атмосферами. Планеты имеют большое количество спутников (некоторые из них по размерам близки к планетам земной группы) и кольца, образованные из мелких частиц и пыли. Особенно заметно кольцо у Сатурна.
Между двойными системами (Земля- Луна, двойные звёзды) есть точка сила гравитации в которой равна нулю. Это так называемая точка Лагранжа L1. Сфера данного радиуса называется полостью Роша. Полость Роша — область вокруг звезды в двойной системе, границей которой служит эквипотенциальная поверхность, содержащая первую точку Лагранжа L1.
В системе координат, вращающейся вместе с двойной звездой, для пробного тела, находящегося в этой области, притяжение звезды, находящейся в полости Роша, преобладает и над притяжением звезды-компаньона, и над центробежной силой.
![]() В точке Лагранжа L1 полости Роша
компонентов двойной системы соприкасаются:
равнодействующая притяжений обеих звёзд обращается в ней в нуль. Это приводит к
возможности перетекания вещества от одной звезды к другой при заполнении одной
из них полости Роша в ходе её эволюции. Такие перетекания играют важную роль
при эволюции тесных двойных звёздных систем (Аккреция).
В точке Лагранжа L1 полости Роша
компонентов двойной системы соприкасаются:
равнодействующая притяжений обеих звёзд обращается в ней в нуль. Это приводит к
возможности перетекания вещества от одной звезды к другой при заполнении одной
из них полости Роша в ходе её эволюции. Такие перетекания играют важную роль
при эволюции тесных двойных звёздных систем (Аккреция).
Пример: Определить линейную скорость движения Земли по орбите вокруг Солнца. Если масса Солнца 1,98 х 1030 кг, а расстояние между центрами Земли и Солнца r = 1,49 х 1011 м. Земля движется вокруг Солнца по окружности с ускорением aц=υ2/r под действием силы
всемирного тяготения, но a =F/m
aц= γ M/r2 приравниваем υ2/r= γ M/r2
![]() υ γM 6,6721011 1,981030 4 м/с
υ γM 6,6721011 1,981030 4 м/с
r = 1,49 11 = 2, 98 х 10
10
Пример: Определить первую космическую скорость, т.е. скорость при которой искусственный спутник Земли будет двигаться по окружности вблизи Земли на расстоянии r ≈ Rз.
Rз = радиус Земли = 6,37x106 м,
М – масса Земли = 5,98 х 1024 кг
![]()
![]() Спутник движется
вокруг Земли по окружности с центростремительным ускорением ац=υ2/r
это ускорение можно определить из второго закона Ньютона a =F/m, F – сила
всемирного тяготения υr2
γmM/rm 2 υr2 γMr2 υ γMr 6,672106,3711105,986 1024 7,9103м/с или, приняв
центростремительное ускорение, примерно равным ускорению свободного падения
имеем: g
Спутник движется
вокруг Земли по окружности с центростремительным ускорением ац=υ2/r
это ускорение можно определить из второго закона Ньютона a =F/m, F – сила
всемирного тяготения υr2
γmM/rm 2 υr2 γMr2 υ γMr 6,672106,3711105,986 1024 7,9103м/с или, приняв
центростремительное ускорение, примерно равным ускорению свободного падения
имеем: g ![]() υ2
υ gr
9,86,37106 7,9103м/с
υ2
υ gr
9,86,37106 7,9103м/с
r
Пример: Определить ускорение, с которым движется спутник на расстоянии 10R от Луны и 60 R от Земли; R – радиус Земли. Известно, что масса Луны в 81 меньше массы Земли. Угол между направлениями со спутника на Луну и на Землю 90o.
![]() Дано: Ускорение
найдем из второго закона Ньютона a =F/m Мз =
Дано: Ускорение
найдем из второго закона Ньютона a =F/m Мз =
81Мл F – равнодействующая сил.
rл = 10 Fл – сила притяжения Луны. R Fз - сила притяжения Земли. rз = 60 Равнодействующую находим по правилу сложения
R векторов, а т.к. угол между направлениями = 90o , то F а = ? находим по теореме Пифагора F2 = Fз2 = Fл2
![]() F FЗ2 FЛ2 γmMЗ
F FЗ2 FЛ2 γmMЗ
FЗ rЗ2 - сила, действующая на спутник со
стороны Земли.
γmMЛ
FЛ ![]() rЛ2 - сила, действующая
на спутник со
rЛ2 - сила, действующая
на спутник со
стороны Луны. Заменим Мл =MЗ/81
![]() FЛ
FЛ
![]() 8100γmMRЗ2 FЗ
8100γmMRЗ2 FЗ ![]() 3600γmMRЗ2 F
100γMRЗm2 811 2 361 2 100gm 0,03 a 0,0003g и
направлено под углом α к направлению на Землю tg α = FЛ/FЗ
= 36/81 = 0,44 α = arсtq 0,
3600γmMRЗ2 F
100γMRЗm2 811 2 361 2 100gm 0,03 a 0,0003g и
направлено под углом α к направлению на Землю tg α = FЛ/FЗ
= 36/81 = 0,44 α = arсtq 0,
44 α = 24o
Ответ: ускорение спутника 0,0003g м/c2
ЗАДАЧИ
1. С какой силой притягивается к Земле тело массой 40 кг, находящееся на высоте 400 км от поверхности Земли? Радиус Земли принять равным 6400 км.
350 Н
2. Определите ускорение свободного падения на Луне, если масса Луны 7,31022 кг. Радиус Луны принять равным 1700 км.
2
1,6 м/с
3. Каково расстояние между покоящимися шарами массой 100 кг каждый, если они притягиваются друг к другу с силой, равной 0,1 Н?
2,58 мм
4. Корабль-спутник «Восток» во время полета находился над землей примерно на высоте 320 км. Радиус Земли 6400 км. С какой силой притягивался корабль к Земле? Масса корабля 4725 кг. 4104 Н
5. Определите ускорение свободного падения на высоте, равной радиусу Земли.
2
2,4 м/с
6. На каком расстоянии от поверхности Земли сила притяжения космического корабля к ней станет в 100 раз меньше, чем на поверхности Земли?
9R3
7. Оцените во сколько раз отличаются силы притяжения вашего тела к Земле и к Солнцу. Расстояние до Солнца считай равным 1,5 108 км.
В 1600 раз
8. Оцените массу Солнца, считая расстояние до Солнца равно 1,5108 км. 21030 кг
Вопросы:
1. Как образовалось Солнце?
2. Как образовалась Солнечная система?
3. Какие планеты Вы знаете?
4. Как классифицируются планеты?
5. Какие точки называются точками Лагранжа?
6. Что называется полостью Роше?
7. Что такое аккреция?
ДОМАШНЕЕ ЗАДАНИЕ 19
1. Найти массу и среднюю плотность Земли. Радиус Земли принять 6400 км. 61024 кг 5,5103кг/м3
2. На каком расстоянии от поверхности Земли ускорение сил тяжести равно 1 м/с2?
13600 км
3. Космическая станция запущена на Луну. Определить точку Лагранжа L1, то есть, на каком расстоянии от центра земли станция будет притягиваться Землей и Луной с одинаковой силой? Считать, что масса Земли больше массы Луны в 81 раз, а расстояние между их центр ми равно 60 земных радиусов.
Х1=54R X2=67,5R
4. На какой высоте над поверхностью Земли сила тяготения уменьшилась на 10%? Радиус Земли считать 6400 км.
350 км
5. Тело подняли на высоту 1600 км над поверхностью Земли. На сколько процентов уменьшилась сила тяготения, действующая на тело?
36 %
24. ВЕС ТЕЛА.
![]() Часто
приходится слышать: «мой вес 70кг». С точки зрения физики это либо, устаревшее
утверждение, либо неверное.
Часто
приходится слышать: «мой вес 70кг». С точки зрения физики это либо, устаревшее
утверждение, либо неверное.
Вес тела – это сила, с которой тело вследствие его притяжения к Земле, действует на опору или натягивает нить подвеса.
Вес – сила, а значит, измеряется в ньютонах, а не килограммах. 70 кг – это ваша масса, а не вес. А сохранилось это с тех времен, когда силу измеряли в килограммах – силы. Сейчас такая единица измерения силы не применяется, поэтому правильно говорить:
«моя масса 70кг»
|
Pm(ga) |
![]() Вес тела
движущегося с ускорением.
Вес тела
движущегося с ускорением.
Поскольку вес тела это сила со стороны опоры, значит он зависит от того как движется эта опора.
Пусть тело находится в лифте, а лифт движется с ускорением направленным вверх. Вес тела Р–сила, с которой тело давит на
пол лифта, но по третьему закону Ньютона эта сила равна силе
реакции опоры PN .
Запишем второй закон Ньютона для тела FТ N ma ,
заменим силу реакции опоры на вес тела FT Pma . Выразим
вес тела PFT ma . Вспомним, что сила тяжести равна
FT mG или FT mg, откуда
Проанализируем этот результат:
1. если лифт движется равномерно или находится в покое а=0 то Р=mg т.е. вес равен силе тяжести.
2. если лифт движется с ускорением, направленным вверх, то в проекциях на ось oy получим: Р = mg-(-a), или Р=m(g+a) - вес больше силы тяжести.
3. если лифт движется с ускорение направленным вниз, то Р = m(g-a) - вес меньше силы тяжести.
4. если лифт будет двигаться с ускорением g вниз , то Р = m(g-g) Р=0 т.е. наступает невесомость. Тело будет свободно падать в месте с лифтом, и не будет давить на опору. Такое состояние наблюдается при движении космических кораблей по орбите вокруг Земли.
Изменение веса тела происходит при движении по выпуклым и вогнутым поверхностям.
Пример: Определить вес мальчика в положениях А и В, движущегося по «американской горке». Радиус кривизны равен 20м, а скорость движения – 5м/с. Масса мальчика равна
40кг.
ДаноВес тела найдём по формуле P m(ga).
: Для случая А в проекциях на y: Р=m(g+a), т.к.
![]() m = ускорение «а» центростремительное и направлено к 40кг центру
окружности, т.е. против оси y. υ = Для случая В: Р=m(g-a), т.к. ускорение
5м/с направлено вдоль оси y (по радиусу).
m = ускорение «а» центростремительное и направлено к 40кг центру
окружности, т.е. против оси y. υ = Для случая В: Р=m(g-a), т.к. ускорение
5м/с направлено вдоль оси y (по радиусу).
R = 2
20м PA m(g ![]() υ ) PA=40(9,8+52/20)=500Н
υ ) PA=40(9,8+52/20)=500Н
Р = ? R2
PB m(g ![]() υ ) PA=40(9,8-52/20)=350Н
υ ) PA=40(9,8-52/20)=350Н
R
Ответ: Вес мальчика в положении А – 500Н, в положении В – 350Н.
ЗАДАЧИ
1. На верхней смотровой площадке телевизионной башни ускорение свободного падения на 0,15 см/с2 меньше, чем у ее основания. На сколько уменьшается сила тяжести, действующая на человека массой 80 кг, при подъеме его на верхнюю смотровую площадку?
2. Космическая ракета при старте с поверхности Земли движется вертикально с ускорением 25 м/с2. Найти вес летчик космонавта в кабине, если его масса 80 кг.
3. Космический корабль на некотором участке вблизи поверхности Земли движется вертикально вверх с ускорением 30 м/с2. С какой силой давит космонавт на кресло кабины, если масса его 80 кг? Какова сила тяжести, действующая на космонавта?
4. Ракета поднимается вертикально вверх с ускорением а = 4g. Каков будет в ней вес тела массой 100 кг? Какая сила тяжести действует на тело?
1. С какой силой давит человек массой 60 кг на пол лифта, движущегося с ускорением 1,2 м/с2: 1) вверх; 2) вниз? С каким ускорением должен двигаться лифт, чтобы человек не давил на пол?
2. Определить силу тяжести, действующую на тело массой 10 кг, поднятое над Землей на расстояние, равное одной четверти земного радиуса.
3. На какой высоте над поверхностью Земли сила тяжести тела будет в три раза меньше, чем на ее поверхности?
4. Парашютист, достигнув в затяжном прыжке скорости 60 м/с, раскрыл парашют, после чего за 4 с его скорость уменьшилась до 10 м/с. Найти вес парашютиста во время торможения, если его масса 80 кг.
ДОМАШНЕЕ ЗАДАНИЕ 20
1. На верхней смотровой площадке Останкинской телевизионной башни ускорение свободного падения на 0,1 см/с2 меньше, чем у ее основания. На сколько уменьшается сила тяжести, действующая на человека массой 80 кг, при подъеме его на верхнюю смотровую площадку?
810-2 Н
2. Космическая ракета при старте с поверхности Земли движется вертикально с ускорением 20 м/с2. Найти вес летчик космонавта в кабине, если его масса 90 кг.
2,7 кН
3. Космический корабль на некотором участке вблизи поверхности Земли движется вертикально вверх с ускорением 40 м/с2. С какой силой давит космонавт на кресло кабины, если масса его 70 кг? Какова сила тяжести, действующая на космонавта?
3,5 кН 700 Н
4. Ракета поднимается вертикально вверх с ускорением а = 3g. Каков будет в ней вес тела массой 10 кг? Какая сила тяжести действует на тело?
5. С какой силой давит человек массой 70 кг на пол лифта, движущегося с ускорением 0,8 м/с2: 1) вверх; 2) вниз? С каким ускорением должен двигаться лифт, чтобы человек не давил на пол?
6. Определить силу тяжести, действующую на тело массой 12 кг, поднятое над Землей на расстояние, равное трети земного радиуса.
66 Н
7. На какой высоте над поверхностью Земли сила тяжести тела будет в два раза меньше, чем на ее поверхности?
2560 км
8. Парашютист, достигнув в затяжном прыжке скорости 55 м/с, раскрыл парашют, после чего за 2 с его скорость уменьшилась до 5 м/с. Найти вес парашютиста во время торможения, если его масса 80 кг. 2,8 кН
25. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
![]()
Из курса 8 класса известно, что все тела состоят из атомов. Атомы состоят из положительного ядра и электронов. Возьмём положительно заряженное тело зарядом Q (тело у которого не хватает некоторого количества электронов, Q = ne, где n – число
потерянных электронов е – заряд одного
электрона, а заряд мера электрического взаимодействия) и внесём в него
небольшой  пробный заряд q. Заряженное тело Q будет
отталкивать тело зарядом q, как будто из Q вытекает некая жидкость (эфир,
физический вакуум) и уносит тело q. Вокруг заряженного тела Q создаётся
электрическое поле, которое передаёт взаимодействие на тело q. Тогда
напряжённость поля, созданного большим зарядом (сила, действующая на единичный,
положительный заряд, внесённый в поле заряда Q), будет
пробный заряд q. Заряженное тело Q будет
отталкивать тело зарядом q, как будто из Q вытекает некая жидкость (эфир,
физический вакуум) и уносит тело q. Вокруг заряженного тела Q создаётся
электрическое поле, которое передаёт взаимодействие на тело q. Тогда
напряжённость поля, созданного большим зарядом (сила, действующая на единичный,
положительный заряд, внесённый в поле заряда Q), будет
направлена от центра большого заряда![]()
![]() где
q – величина, характеризующая электрическое взаимодействие и называемая зарядом
(измеряется в Кулонах). Линии напряжённости (линия, в каждой точке которой
вектор напряжённости является касательным), будут выглядеть так, как на
рисунке. Куда бы мы не поместили пробный заряд, на него будет действовать сила,
направленная по линии, соединяющей центры тел. Положительный заряд, будет
отталкиваться от положительного, вытекать из источника и притягиваться к
отрицательному заряду, втекать в сток.
где
q – величина, характеризующая электрическое взаимодействие и называемая зарядом
(измеряется в Кулонах). Линии напряжённости (линия, в каждой точке которой
вектор напряжённости является касательным), будут выглядеть так, как на
рисунке. Куда бы мы не поместили пробный заряд, на него будет действовать сила,
направленная по линии, соединяющей центры тел. Положительный заряд, будет
отталкиваться от положительного, вытекать из источника и притягиваться к
отрицательному заряду, втекать в сток.
Представим вокруг заряда Q
сферу. Тогда поток вектора напряжённости электрического поля Е⃗⃗ равен
Ф=EScosα. По теореме Остроградского-Гаусса Ф=![]() 𝑄 , где Q – сумма
зарядов, находящихся внутри сферы или заряд образующий поле, ε -
относительная диэлектрическая проницаемость среды, εо –
электрическая постоянная. Тогда ES=Q/εεо, а 𝑆 = 4𝜋𝑅2.
Отсюда
𝑄 , где Q – сумма
зарядов, находящихся внутри сферы или заряд образующий поле, ε -
относительная диэлектрическая проницаемость среды, εо –
электрическая постоянная. Тогда ES=Q/εεо, а 𝑆 = 4𝜋𝑅2.
Отсюда
Е= ,
![]() 𝜋𝜀𝜀о
𝜋𝜀𝜀о
тогда сила взаимодействия между точечными или сферическими телами
равна
![]() F=qE
или
F=qE
или ![]() F
F
Эта формула выражает закон Кулона
![]() Сила взаимодействия между покоящимися точечными
заряженными телами прямо пропорциональна произведению зарядов и обратно
пропорциональна квадрату расстояния между ними.
Сила взаимодействия между покоящимися точечными
заряженными телами прямо пропорциональна произведению зарядов и обратно
пропорциональна квадрату расстояния между ними.
Электрическое взаимодействие осуществляется по схеме тело-поле-тело.
Электромагнитное взаимодействие – это взаимодействие электронов и протонов. Классическое представление о строении атома (планетарная модель) таково: в центре атома находится ядро, состоящее из протонов и нейтронов (частиц, не имеющих заряда), а вокруг ядра подобно планетам движутся электроны по
своим орбитам. Положительный заряд ядра равен отрицательному заряду всех электронов и в сумме заряд равен нулю, т.е. атом нейтрален. Сумма протонов и нейтронов приблизительно равна массе ядра, выраженной в атомных единицах массы, и называется массовым числом. Сумма протонов называется зарядовым числом.
Проведём аналогии между полем скоростей и электрическим полем. С точки зрения математики всё, что написано ниже одно и то же, только буквы разные. Если считать, что источником струйки или потока жидкости является массовый расход жидкости, то
Ф=υS;
Ф=![]() 1 (𝑚);
1 (𝑚); ![]()
![]() 1 Если
считать, что источником электрического поля является заряд, а аналогична
1 Если
считать, что источником электрического поля является заряд, а аналогична ![]() ,
,
то
Ф=ЕS;
Ф=![]() ; p
; p![]()
Поэтому, если для потока жидкости давление равно плотности кинетической энергии, то для электрического поля давление, оказываемое на заряженную плоскость, находящуюся в электрическом поле равно плотности энергии электрического поля.
Найдём энергию электрического поля, образованного двумя разноимённо
заряженными параллельными пластинами (конденсатор). Плотность энергии
электрического поля равна![]()
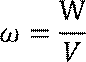
Где ω – плотность энергии, W – энергия электрического поля, V – объём поля. Отсюда W=ωV. Объём между пластинами равен V=dS, где d – расстояние между пластинами,S – площадь пластины.
![]() . Из курса физики 8класса известно, что напряжение между
пластинами
. Из курса физики 8класса известно, что напряжение между
пластинами
конденсатора U, это работа по перемещению единичного положительного заряда. Работа по определению это сила, умноженная на перемещение. Тогда для единичного заряда имеем qU = qEd, U=Ed, где d – перемещение заряда вдоль силовой линии. Подставляя в формулу для
энергии электрического поля ![]() получаем
получаем ![]() , или
, или![]() , или
, или
![]()
![]() , где
, где ![]() - электрическая ёмкость
плоского конденсатора.
- электрическая ёмкость
плоского конденсатора.
Задачи
Пример: В вершинах при основании прямоугольного равнобедренного треугольника расположены одинаковые точечные заряды Q1 = Q2 = 2х10-8 Кл. Расстояние AB между зарядами равно 0,6 м. Определить силу, действующую на заряд Q3 = -3 х10-8 Кл,
находящийся в вершине угла C.
![]() Дано:
Дано:
Q1 = Q2 =
2х10-8 Кл
Q3 = - 3х10-8
Кл L = AB = 0,6 м F = ?
Силу F найдем, как
FF1 F2 ΔАВС равнобедренный АС= ВС;
∠АСВ = 90о, значит все параллелограммы, образованные на сто-ронах АС и СВ будут прямоугольниками, а ΔСFF2 прямо-угольным. Поэтому
![]() F F12 F22 ,
F F12 F22 ,
![]() F1
F1 ![]() k Qr12Q3 , F2
k Qr12Q3 , F2 ![]() k Qr22Q3 , r = AC = CD Q1=Q2
F1 = F2, F= 2F1 = 2F2 ,
k Qr22Q3 , r = AC = CD Q1=Q2
F1 = F2, F= 2F1 = 2F2 ,
L2=R2+R2
![]()
![]() R2=L2/2 F= 2
Q1 rQ2 3 2 , F= 9109 21008,632 108 2
2 , F=424107 (H) Ответ: сила, действующая
на заряд Q3 равна 4,2х10-5Н.
R2=L2/2 F= 2
Q1 rQ2 3 2 , F= 9109 21008,632 108 2
2 , F=424107 (H) Ответ: сила, действующая
на заряд Q3 равна 4,2х10-5Н.
Пример: Заряд электрона е = 1, 6x10-19 Кл.
Определить скорость движения электрона по орбите атома водорода, если её радиус равен
R=5,3x10-11м.
![]()
![]() Дано:
Электрон и протон взаимодействуют по
Дано:
Электрон и протон взаимодействуют по
19 e =-1,6x10-закону Кулона F= 4Qππε1 Qor22 , по второму закону Кл
m=9,11х10-
31кг = 8, Ньютона ускорение а=υF=ma2, где а /r – центростре-мительное εo
![]()
![]() 85x10 r = 5,3x10–12 -11
4Qπ1εQor22 =m υr2 υ= 4πeε2orm
85x10 r = 5,3x10–12 -11
4Qπ1εQor22 =m υr2 υ= 4πeε2orm
м
υ = ? υ=
(1,61019)2
12 5,31011 9,111031
43,148,8510
υ=2200x103м/с υ=2200км/с
Ответ: скорость электрона в атоме водорода 2200 км / сек.
![]() Определим частоту
вращения электрона вокруг ядра: υ=2πrn
n=υ/2πr n= 2π22005,31010311 14 1
Определим частоту
вращения электрона вокруг ядра: υ=2πrn
n=υ/2πr n= 2π22005,31010311 14 1
6610 сек
Частота вращения электрона вокруг ядра атома водорода n равна 66х1014 сек-1.
Взаимодействовать электрически могут и нейтральные системы, у которых заряды расположены не симметрично. Система, состоящая из двух зарядов q, равных по абсолютной величине, но противоположных по знаку называется диполем. Рассмотрим взаимодействие двух диполей, расстояние между которыми много больше плеча диполя ( расстояние между его зарядами).
Сила взаимодействия складывается из 4-х компонентов
![]() F (q)(2q) (q)(q2 ) (q)(q) 2 (q)(q) 2
F (q)(2q) (q)(q2 ) (q)(q) 2 (q)(q) 2
4εor 4or 4o (r L) 4o (r L) q2 2 1 1
![]() F 4πo r2 (rL)2 (rL)2
F 4πo r2 (rL)2 (rL)2
6q2L2 (r2 L2 3)
F 2 2 2 2 , пренебрегая L- по сравнению с r получим
4πo r (r L )
F ![]() 6q2L42 ,
6q2L42 ,
4πor
итак, два диполя будут притягиваться, причем силы будут быстро убывать с
расстоянием.

ВОПРОСЫ:
1. Какие элементарные заряженные частицы вы знаете?
2. Как устроен атом?
3. Что такое заряженное тело?
4. Что такое электрическое поле?
5. Что такое напряжённость электрического поля по определению?
6. В каких единицах измеряется напряжённость электрического поля?
7. Что называется линиями напряжённости электрического поля?
8. Как направлены линии напряжённости точечного положительного заряда?
9. Как направлены линии напряжённости отрицательного точечного заряда?
10. Как направлены линии напряжённости диполя?
11. Чему равна напряжённость электрического поля, образованного точечным или сферическим зарядом?
12. Сформулируйте закон Кулона
13. Чему равна плотность энергии электрического поля?
14. Чему равна энергия плоского конденсатора?
15. Чему равна ёмкость плоского конденсатора?
ЗАДАЧИ
1. Два одинаковых точечных заряда взаимодействуют в вакууме с силой 0,3 Н. Расстояние между зарядами 2м. Найти величину этих зарядов.
2. Два заряда по 1,1•10-8 Кл, Разделённые слоем слюды, взаимодействуют с силой 54•102 Н. Определить толщину слоя слюды, если её диэлектрическая проницаемость равна 8.
3. Заряд в 1,9•10-9 Кл в керосине на расстоянии 0,002м притягивает к себе второй заряд с силой 1,5•10-4 Н. Найдите величину второго заряда. Диэлектрическая проницаемость керосина равна 2.
4. Проводящий шарик, несущий заряд 2,8•10-8 Кл, привели в соприкосновение с такими же двумя шариками, один из которых имел заряд -0,8•10-8 Кл, а другой был не заряжен. Как распределился заряд между шариками? С какой силой будут взаимодействовать в вакууме два из них на расстоянии 4 см один от другого?
5. В ядре атома меди 63 частицы, из них 29 протонов. Сколько нейтронов и электронов находится в этом атоме?
6. Два точечных заряда действуют друг на друга с силой 12 Н. Какой будет сила взаимодействия, если уменьшить величину каждого заряда в 2 раза не меняя расстояние.
7. Как изменится модуль напряжённость электрического поля, созданного точечным зарядом, при увеличении расстояния от этого заряда до точки наблюдения в N раз?
8. Как изменится ёмкость плоского воздушного конденсатора, если площадь обкладок увеличить в 2 раза, а расстояние между ними уменьшить в 2 раза?
9. В вершинах равностороннего треугольника со стороной а находятся заряды +q, +q и -
q. Найти напряженность поля в центре треугольника.
E=6kq/a2
ДОМАШНЕЕ ЗАДАНИЕ 21
1. Два одинаковых точечных заряда взаимодействуют в вакууме с силой 0,1 Н. Расстояние между зарядами 6м. Найти величину этих зарядов.
0,2 мкКл
2. Два заряда по 3,3•10-8 Кл, Разделённые слоем слюды, взаимодействуют с силой 5•10-2 Н. Определить толщину слоя слюды, если её диэлектрическая проницаемость равна 8.
-3 м.
5•10
3. Заряд в 1,3•10-9 Кл в керосине на расстоянии 0,005м притягивает к себе второй заряд с силой 2•10-4 Н. Найдите величину второго заряда. Диэлектрическая проницаемость керосина равна 2.
-9 Кл.
0,8•10
4. Проводящий шарик, несущий заряд 1,8•10-8 Кл, привели в соприкосновение с такими же двумя шариками, один из которых имел заряд -0,3•10-8 Кл, а другой был не заряжен. Как распределился заряд между шариками? С какой силой будут взаимодействовать в вакууме два из них на расстоянии 5 см один от другого?
-8 Кл.
0,5•10
5. Два заряда, один из которых по модулю в 4 раза больше другого, расположены на расстоянии а друг от друга. В какой точке пространства напряженность поля равна нулю, если заряды разноименные?
На прямой, соединяющей заряды, на расстоянии а от меньшего и 2а от большего.
6. Ромб составлен из двух равносторонних треугольников со стороной, длина которой равна 0,2 м. В вершинах при острых углах ромба помещены одинаковые положительные заряды по 6 • 10-7 Кл. В вершине при одном из тупых углов помещен отрицательный заряд 8
• 10-7 Кл. Определить напряженность электрического поля в четвертой вершине ромба.
4,5•104 В/м
7. Как изменится ёмкость плоского воздушного конденсатора, если площадь обкладок и расстояние между ними уменьшить в 4 раза?
8. Определить ёмкость плоского конденсатора, если перекрываемая площадь пластин 2см2, расстояние между пластинами 0,01мм, между пластинами слюда.
26. МАГНИТНОЕ ПОЛЕ
![]() При
движении одноимённых зарядов в одном направлении сила взаимодействия
(отталкивания) уменьшается, а в разных – увеличивается. Силу взаимодействия
можно представить как
При
движении одноимённых зарядов в одном направлении сила взаимодействия
(отталкивания) уменьшается, а в разных – увеличивается. Силу взаимодействия
можно представить как
F = Fэ – Fм (υ), где
F – сила электромагнитного взаимодействия, Fэ - сила электрического взаимодействия между покоящимися зарядами, – сила электрическая,
![]() электростатическая,
кулоновская, электрическая составляющая электромагнитного
взаимодействия. Fм(υ) - сила магнитного взаимодействия. В
чистом виде магнитное взаимодействие наблюдается между проводниками
с током, когда электрическое взаимодействие
компенсируется. Вокруг проводника с током возникает магнитное поле, которое
передаёт взаимодействие второму проводнику с током и наоборот. Характеристикой
магнитного поля является напряжённость магнитного поля. За направление
напряжённости магнитного поля берётся направление свободно установившейся
магнитной стрелки. Рассмотрим магнитное поле прямого тока. Магнитные стрелки
(компасы) выстраиваются перпендикулярно проводнику (опыт Эрстеда). Линии
напряжённости будут представлять собой окружности. Магнитное поле,
образованное проводником с током является вихревым и описывается циркуляцией
вектора ⃗Н⃗⃗
, но чаще пользуются другой характеристикой магнитного поля вектором
магнитной индукции поля
электростатическая,
кулоновская, электрическая составляющая электромагнитного
взаимодействия. Fм(υ) - сила магнитного взаимодействия. В
чистом виде магнитное взаимодействие наблюдается между проводниками
с током, когда электрическое взаимодействие
компенсируется. Вокруг проводника с током возникает магнитное поле, которое
передаёт взаимодействие второму проводнику с током и наоборот. Характеристикой
магнитного поля является напряжённость магнитного поля. За направление
напряжённости магнитного поля берётся направление свободно установившейся
магнитной стрелки. Рассмотрим магнитное поле прямого тока. Магнитные стрелки
(компасы) выстраиваются перпендикулярно проводнику (опыт Эрстеда). Линии
напряжённости будут представлять собой окружности. Магнитное поле,
образованное проводником с током является вихревым и описывается циркуляцией
вектора ⃗Н⃗⃗
, но чаще пользуются другой характеристикой магнитного поля вектором
магнитной индукции поля ![]() . Вектор
магнитной индукции аналогичен напряжённости магнитного поля Н⃗ . В⃗ = 𝛍𝛍𝟎Н⃗⃗ и численно
равен силе, действующей на проводник с током длиной 1 метр, находящийся в
магнитном поле по которому протекает ток 1 ампер. μμо –
соответственно относительная магнитная
проницаемость среды и магнитная постоянная.
. Вектор
магнитной индукции аналогичен напряжённости магнитного поля Н⃗ . В⃗ = 𝛍𝛍𝟎Н⃗⃗ и численно
равен силе, действующей на проводник с током длиной 1 метр, находящийся в
магнитном поле по которому протекает ток 1 ампер. μμо –
соответственно относительная магнитная
проницаемость среды и магнитная постоянная.
![]() .
.
За направление вектора магнитной индукции берётся направление свободно установившейся магнитной стрелки. Куда бы мы ни поставили компас (магнитную стрелку) около провода с током, всегда она будет располагаться, перпендикулярно проводу (опыт Эрстеда). Из опыта Эрстеда следует, что линии вектора магнитной индукции – концентрические окружности.
Циркуляция вектора магнитной индукции вдоль окружности равна:
![]() .
.
Исходя из симметрии окружности и однородности пространства - В – постоянная величина. Тогда
Г=В(∆ℓ1+∆ℓ2+∆ℓ3+∆ℓ4+…). Г=Вℓ, Г=В·2πR. Источником магнитного поля являются токи. Закон полного тока гласит: циркуляция индукции магнитного поля пропорциональна сумме токов охваченных контуром Г=μμ0I, отсюда В·2πR= μμ0I, а
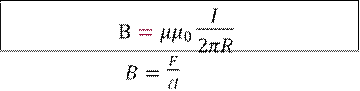 Из формулы , следует, что сила,
действующая на проводник с током в однородном магнитном поле равна F=ВℓI.
С учётом того, что [⃗В⃗⃗
· ⃗ℓ⃗] – векторное произведение, модуль силы равен
Из формулы , следует, что сила,
действующая на проводник с током в однородном магнитном поле равна F=ВℓI.
С учётом того, что [⃗В⃗⃗
· ⃗ℓ⃗] – векторное произведение, модуль силы равен
F=ВℓIsinα.
Это сила Ампера. Сила, действующая на проводник с током в магнитном поле. Очевидно, что если сила Ампера действует на проводник с током (движущимися зарядами), то на каждый движущийся заряд действует сила.
Сила тока – это заряд, проходящий по проводнику за единицу времени.I=Q/t,
Тогда
![]() , где q заряд одной частицы, а N – число частиц, а если разделить
обе части уравнения на число частиц, находящихся в проводнике, то получим
силу, действующую на один заряд – силу Лоренца.
, где q заряд одной частицы, а N – число частиц, а если разделить
обе части уравнения на число частиц, находящихся в проводнике, то получим
силу, действующую на один заряд – силу Лоренца.
𝐹л = 𝑞𝑣𝐵 sin 𝛼,
где α – угол между скоростью и вектором магнитной индукции. Направление силы (сила
Лоренца) и силы Ампера определяется по правилу левой руки.
Линии магнитной индукции входят в ладонь. Четыре пальца по направлению силы тока или по направлению движения положительного заряда, против отрицательного. Большой отогнутый палец даёт направление силы Ампера и силы Лоренца.
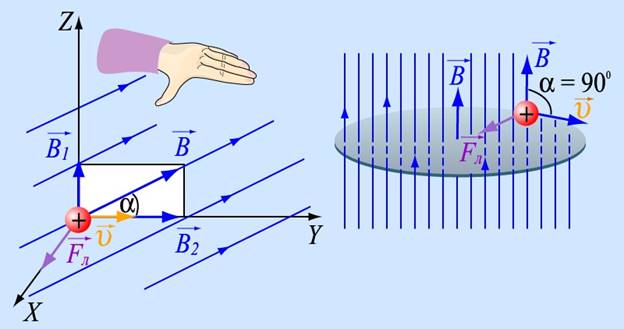
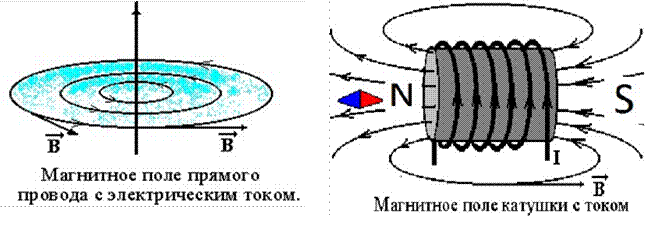
Магнитное поле изображается линиями магнитной индукции. Линия магнитной индукции – это линия в каждой точке которой, вектор индукции магнитного поля является касательным. Линии индукции магнитного поля являются замкнутыми линиями, а магнитное поле, называется вихревым полем.
Направление линий определяется по северному концу магнитной стрелки.
Направление линий магнитной индукции определяется так же по правилу «буравчика»: Если направление поступательного движения буравчика (правого винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линии магнитной индукции и наоборот, если направление вращения ручки буравчика совпадает с направлением электрического тока в катушке, то поступательное движение буравчика совпадает с направлением линий магнитной индукции.
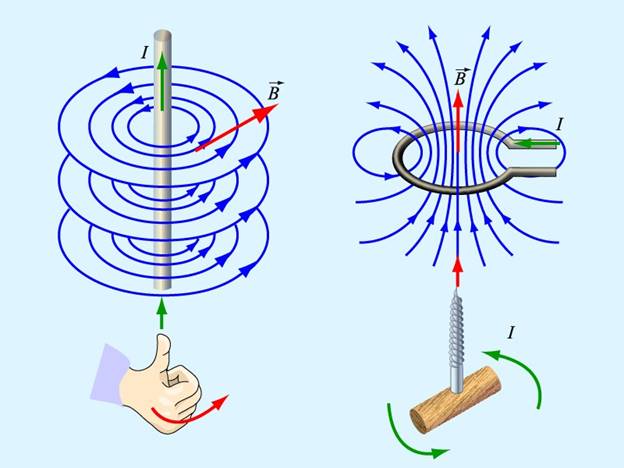
Рисунок 1 правило правой руки и правило "буравчика"
Если длина соленоида (электрической катушки) много больше её диаметра, то магнитное поле внутри можно считать однородным. Линии магнитной индукции параллельны, а величина вектора магнитной индукции одинакова во всех точках.
Определим индукцию магнитного поля внутри длинной катушки (соленоид). Выберем замкнутый контур (линия красного цвета). Циркуляция вектора магнитной индукции по замкнутому контуру равна:
Г=![]() . Г = Ввнутр(∆ℓ1+∆ℓ2+∆ℓ3+∆ℓ4+…)+ Ввнеш(∆ℓ1+∆ℓ2+∆ℓ3+∆ℓ4+…).
. Г = Ввнутр(∆ℓ1+∆ℓ2+∆ℓ3+∆ℓ4+…)+ Ввнеш(∆ℓ1+∆ℓ2+∆ℓ3+∆ℓ4+…).
Поле вне катушки приравняем к нулю, в данный момент оно нас не интересует. Тогда Г=Вℓ, где ℓ - длина катушки. По закону полного тока В·ℓ= μμ0IW, где N – число витков катушки. Отсюда
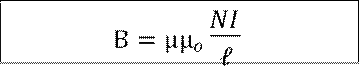
Магнитное поле также обладает энергией. Плотность энергии рассчитывается по формуле, аналогичной плотности энергии векторных полей (поля скоростей и поля электростатического).
![]() 𝜌𝜐2
𝜌𝜐2
ω = ![]()
2
Или используя вектор магнитной индукции
B2
𝜔
= ![]() 2µµо
2µµо
Определим энергию магнитного поля катушки с током.
W=ωV, 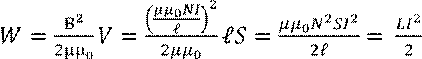
Где L![]() - индуктивность катушки.
- индуктивность катушки.
|
𝒎𝝊𝟐 𝑾к = |
|
𝑪𝑼𝟐 𝑾э =
|
|
𝑳𝑰𝟐 𝑾м = |
|
𝟐 𝟐 𝟐
Что касается силы взаимодействия между движущимися заряженными частицами, то она
|
q q q q F F F 1 2 1 1 2 2 э м 4πεε r2 4c2r2 o 0 |
будет равна:
Вопросы:
1. Как меняется сила взаимодействия между электрическими зарядами при их движении?
2. Как можно представить силу взаимодействия между движущимися зарядами?
3. Где наблюдается чисто магнитное взаимодействие?
4. Как происходит взаимодействие двух проводников с током?
5. Что берётся за направление вектора напряжённости магнитного поля?
6. Чему равен модуль вектора магнитной индукции по определению?
7. Как связаны вектор напряжённости магнитного поля и вектор магнитной индукции?
8. О чём говорит закон полного тока?
9. По какой формуле определяется вектор магнитной индукции от прямого тока?
10. Чему равна сила Ампера?
11. Что такое сила Лоренца?
12. Чему равна сила Лоренца?
13. Как определить направление силы Лоренца?
14. Как определить направление силы Ампера?
15. Как изображается магнитное поле?
16. Что называется линиями магнитной индукции?
17. Как направлены линии магнитной индукции?
18. Сформулируйте правило буравчика.
19. Чему равен вектор магнитной индукции внутри соленоида?
20. Чему рано динамическое давление жидкости?
21. Чему равна плотность энергии электрического поля?
22. Чему равна плотность энергии магнитного поля?
23. Чему равна энергия магнитного поля соленоида?
24. Чему равна индуктивность соленоида?
25. Чему равна энергия движущегося тела?
26. Чему равна энергия конденсатора? 27. Как найти энергию магнитного поля катушки?
Задачи: 1. Какова индукция магнитного поля, в котором на проводник с длиной активной части 5 см действует сила 50 мН? Сила тока в проводнике 25 А. Проводник расположен перпендикулярно индукции магнитного поля.
40 мТл
2. В однородном магнитном поле с индукцией 0,8 Тл на проводник с током в 30 А, длина активной части которого 10 см, действует сила 1,5 Н. Под каким углом к вектору индукции расположен проводник?
39о
3. Какова сила тока в проводнике, находящемся в однородном магнитном поле с индукцией 2 Тл, если длина активной части проводника 20 см, сила, действующая на проводник, 0,75 Н, а угол между направлением линий индукции и током 49°?
2,5 А
ДОМАШНЕЕ ЗАДАНИЕ 22
1. Какова индукция магнитного поля, в котором на проводник с длиной активной части 4 см действует сила 40 мН? Сила тока в проводнике 25 А. Проводник расположен перпендикулярно индукции магнитного поля.
2. Какова сила тока в проводнике, находящемся в однородном магнитном поле с индукцией 1,5 Тл, если длина активной части проводника 10 см, сила, действующая на проводник, 0,6 Н, а угол между направлением линий индукции и током 49°?
29. ДВИЖЕНИЕ ТЕЛА В ОДНОРОДНЫХ ПОЛЯХ.
1. Движение тела в однородном гравитационном поле.
a) Движение тела, брошенного вертикально.
Пример: с балкона на высоте 25м от земли вертикально вверх бросили мяч со скоростью 20м/с. Определить время движения до Земли и скорость во время падения?
Запишем второй закон Ньютона Fma.
Дано:
![]() υо=20м/с Сила
тяжести равна FmG aG или yo=25м ag
. Запишем уравнение движения at2
υо=20м/с Сила
тяжести равна FmG aG или yo=25м ag
. Запишем уравнение движения at2
Gt==9? ,8Н/кг S
υot ![]() 2 . Спроецируем его на
оси
2 . Спроецируем его на
оси
υo=? y=yo+υot-gt2/2
в момент падения y=0, поэтому 0=25+20t-5t2 t2-4t-5=0 t=5 c.
υ υo gt в проекциях υ=υо-gt υ=20-9,8x5=-30 м/с
Ответ: время нахождения в полёте – 5 секунд, скорость при падении – 30 м/с, скорость направлена против оси y.
a) Движение тела, брошенного горизонтально.
Пример: С самолета произведен выстрел горизонтально с начальной скоростью 800 м/с. На сколько снаряд отклонился от горизонтали, если до цели 500м?
![]() Дано: Наравим oсь y
вниз. υо=800м/с Запишем второй закон Ньютона
Дано: Наравим oсь y
вниз. υо=800м/с Запишем второй закон Ньютона
S=500м Fma,на тело действует только h=? сила тяжести.
FmG ag
Запишем уравнение движения:
S
υot ![]() , в проекциях –
, в проекциях –
2
![]() Sx=
υot t = Sx/υo
Sx=
υot t = Sx/υo
Sy = gt2/2 Sy=
h= g ![]() 2Sυ2xo2
2Sυ2xo2
9,85002
h= ![]() 28002 1,9м
28002 1,9м
Ответ: снаряд сместится вниз от горизонтального движения на 1,9 метра.
b) Движение тела, брошенного под углом к горизонту.
Пример: Найти высоту подъема и дальность полета сигнальной ракеты, выпущенной со скоростью 40 м/с под углом 60o к горизонту?
Дано: Запишем второй закон Ньютона Fma,
о
![]() α=60 на
тело действует только сила тяжести
α=60 на
тело действует только сила тяжести
υо=40м/с FmG, поэтому aG или ag
Нmax-?
L - ? Запишем at2 уравнение движения:
2
В проекциях на оси координат:
Sx=υoxt
Sy=υoyt-gt2/2
![]()
![]() υox=υocosα
xo=0 x = υotcosα υoy=υosinα
yo=0 y = υotsinα –gt2/2
υox=υocosα
xo=0 x = υotcosα υoy=υosinα
yo=0 y = υotsinα –gt2/2
При падении y=0 0=34,64t-5t2 t=7c L=х= υotcosα =20x7=140м
![]() S υυo , на максимальной Для
нахождения высоты полёта воспользуемся формулой
S υυo , на максимальной Для
нахождения высоты полёта воспользуемся формулой
2a
![]() υoy2 35 высоте υy=0
Sy Hmax , Н= 61,25м 2g 29,8
υoy2 35 высоте υy=0
Sy Hmax , Н= 61,25м 2g 29,8
Ответ: время полёта – 7 секунд, дальность полёта – 140 метров, высота подъёма – 61,25 м.
2. Движение в однородном электрическом поле.
1. Пусть заряженное тело находится в однородном электрическом поле υо=0. Тогда на
него действует сила FЭ Еq, но по второму
закону
Ньютона Fma Eq
ma
a ![]() - движение
- движение
m
Еq
равноускоренное. υ ![]() t скорость возрастает,
поэтому поле называется ускоряющим.
t скорость возрастает,
поэтому поле называется ускоряющим.
m
2
Eqt
Перемещение
находим по формуле S ![]() 2m
2m
2. Пусть положительное тело движется против силовых линий.
![]()
Запишем второй закон Ньютона Fma . На тело действует только сила со стороны электрического поля
qE qE
FЭ qE
a ![]() υх =
υox - axt υx υox
υх =
υox - axt υx υox ![]() m m
m m
qEt2
Sx υoxt ![]() - движение равнозамедленное,
скорость
- движение равнозамедленное,
скорость
2m
уменьшается. Такое поле называют тормозящим.
3. Электрон движется перпендикулярно силовым линиям напряженность поля E = 5 В/м со скоростью υo= 500 м /с. На сколько произойдет смещение от прямолинейного движения при длине поля S= 0,01 м?
![]() ,
в проекциях на оси:
,
в проекциях на оси:
ох
Sy ![]() 2m 2 или h
2m 2 или h
![]() 21,61027 5002
0,01м
21,61027 5002
0,01м
υox
Ответ: электрон отклоняется от горизонтального движения в поперечном электрическом поле на 0,01 м.
Изменяя величину и направление напряженности электрического поля, можно отклонить частицу (потоки частиц) в ту или другую сторону, что используется в измерительной технике, осциллографах.
1. Положительно заряженная капелька жидкости находится в равновесии в однородном электрическом поле, направленном вертикально вверх напряженностью 98 Н/Кл. Определить заряд капельки, если её масса 10-4 г.
Дано: Капелька находится в
![]() E
= 98 Н/Кл однородном гравитационном G = 9,8 Н/ кг поле
Земли и в электрическом m = 10-7 кг поле.
На неё действуют силы: q = ? FТ mG и
E
= 98 Н/Кл однородном гравитационном G = 9,8 Н/ кг поле
Земли и в электрическом m = 10-7 кг поле.
На неё действуют силы: q = ? FТ mG и
FЭ qЕ . Запишем второй
закон Ньютона Fma или
FТ FЭ ma в проекциях на ось y
FТ-FЭ=0 так как капелька нахо-
дится в равновесии
Gm
Eq
= Gm q = ![]()
E
q = ![]() 9,8107 108 Кл.
9,8107 108 Кл.
98
Ответ: чтобы капелька находилась в равновесии, заряд капельки должен равняться 10-8 Кл.
2. В тормозящее электрическое поле толщиной 2см и напряжённостью 100 Н/Кл влетает заряженная частица массой 0,1г и зарядом 2·10-4Кл. С какой начальной скоростью должна лететь частица, чтобы преодолеть это поле?
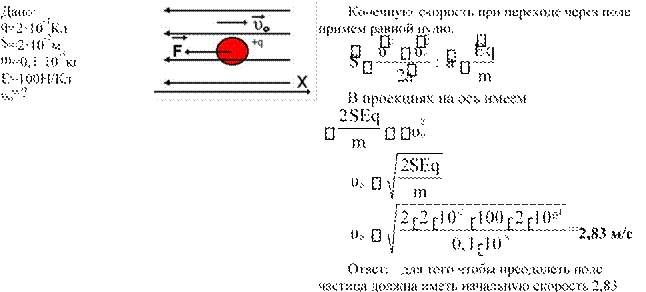
м/с.
3. Движение частицы в магнитном поле.
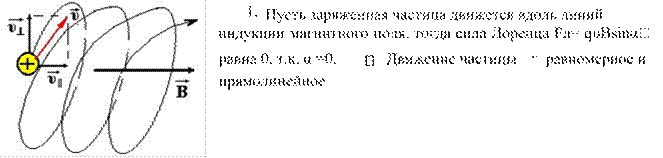
2. Пусть скорость частицы перпендикулярна линиям магнитной индукции однородного
магнитного поля, т.е. Bυ, тогда сила Лоренца является центростремительной силой, т.к.
направлена перпендикулярно скорости и движение будет происходить по окружности,
радиус которой можно определить. Запишем II-й закон Ньютона Fma , но F=qυB отсюда mυ 2 mυ
![]()
qBυ
r
qBυ
r ![]() r qB
r qB
3. Частица движется под углом к силовым линиям. Тогда скорость υ можно разложить
на υ - перпендикулярную B иυ параллельную B . Тогда υ задает движение частицы по
окружности, а υ - это скорость с которой окружность движется вдоль вектора магнитной
индукцииВ , а итогом будет движение частицы по винтовой линии.
С помощью магнитных полей можно управлять движением заряженных частиц, что широко используется в телевидении и ускорительной технике.
Пример: Электрон влетает в однородное магнитное поле со скоростью 16000 кмм/с перпендикулярно его линиям магнитной индукции. Определить модуль магнитной индукции поля, если электрон движется по окружности радиусом 1 см.
Дано: На электрон, влетающий в однородное
![]() υ=1,6·107м/с
магнитное поле, действует сила Лоренца, поэтому α=90о mυ2
υ=1,6·107м/с
магнитное поле, действует сила Лоренца, поэтому α=90о mυ2
r=10-2м Besin ![]() m=9?1·10-31кг r
m=9?1·10-31кг r
q=1,6·10-19Кл B ![]() mυ
; В=? ersinα
mυ
; В=? ersinα
9,110-31 1,6107 3
B ![]() 9,110 Të
9,110 Të
1,610-19 102
Ответ: индукция магнитного поля равна 9,1·10-3 Тл.
Пример: на какой угол от первоначального движения отклонится электрон в магнитном поле толщиной 5см и индукцией 2х10-4 Тл, если скорость его 3,5х 106 м/с
![]() Дано Магнитное поле
направлено
h= 5х10-2м чертежу за чертеж. Электрон будет
Дано Магнитное поле
направлено
h= 5х10-2м чертежу за чертеж. Электрон будет
двигаться по дуге окружности
В= 2х10-4Тл
радиуса r и, вылетев из поля, будет
υ= 3,5х106м/с двигаться равномерно и m=9,1х10-31кг прямолинейно. Как видно из
чертежа угол α равен
e= 1,6х10-19кл
α=? h
α=
90-β , сosβ ![]() , радиус r
, радиус r
2
найдем из 2-го закона Ньютона Fл =ma, где сила Лоренца Fл=
qυB, а ![]() υ -
υ -
r
mυ hqB 5102 1,61019 2104
центростремительное ускорение r
![]() qB
cosβ
qB
cosβ
![]() m = 9,1 1031 3,5106 0,5
m = 9,1 1031 3,5106 0,5
υ
=arccos0,5=60o α= 90o-60o=30o
Ответ: электрон отклонился в магнитном поле на угол 30о от первоначального движения.
ДОМАШНЕЕ ЗАДАНИЕ 23
1.С балкона на высоте 40м от земли вертикально вверх бросили мяч со скоростью
25м/с. Определить время движения до Земли и скорость во время падения?
![]()
2.Электрон влетает в электрическое поле против силовых линий. Напряжённость поля 2•10-8 В/м. Сколько времени потребуется ему для возврата в исходную точку, если начальная скорость электрона 2•106 м/с.
3.С самолета, летящего со скоростью 200 м/с произведен выстрел горизонтально с начальной скоростью 600 м/с. На сколько снаряд отклонился от горизонтали, если до цели 500м? 4. Капелька жидкости находится в равновесии в восходящем потоке воздуха, направленном вертикально вверх. Определить массу капельки, если сила сопротивления воздуха
2•10-4 Н.
5. Положительно заряженная капелька жидкости находится в равновесии в однородном электрическом поле, направленном вертикально вверх напряженностью 196 Н/Кл. Определить заряд капельки, если её масса - 2•10-4 г.
6. С какой начальной скоростью необходимо бросить мяч вертикально вверх, чтобы он преодолел высоту 30м.
7. В тормозящее электрическое поле толщиной 3см и напряжённостью 200 Н/Кл влетает заряженная частица массой 0,2г и зарядом 4·10-4Кл. С какой начальной скоростью должна лететь частица, чтобы преодолеть это поле?
8. Электрон влетает в однородное магнитное поле со скоростью 16000 кмм/с перпендикулярно его линиям магнитной индукции. Определить модуль магнитной индукции поля, если электрон движется по окружности радиусом 1 см.
9. Электрон, влетающий в однородное магнитное поле под углом 60о к направлению поля, движется по винтовой линии радиусом 5см с периодом обращения 60мкс. Какова скорость электрона, индукция магнитного поля и шаг винтовой линии?
10.
На какой угол от первоначального движения отклонится электрон в
магнитном поле толщиной 4см и индукцией 2х10-4 Тл, если скорость его
2,5х 105 м/с ![]() .
.
11. Два тела брошены вертикально вверх из одной точки вслед одно за другим с интервалом времени τ и с одинаковыми начальными скоростями υо. Через сколько времени оба тела встретятся?
12. Мяч брошен с поверхности земли под углом 30о к горизонту с начальной скоростью υо = 14 м/с. На расстоянии 11 м от точки бросания находится гладкая стена. На каком расстоянии от точки броска мяч упадёт на землю после абсолютного удара о стену?
![]() 28. СИЛЫ ТРЕНИЯ.
КОЭФФИЦИЕНТ ТРЕНИЯ. ТРЕНИЕ В ЖИДКОСТЯХ И ГАЗАХ. УЧЁТ И
28. СИЛЫ ТРЕНИЯ.
КОЭФФИЦИЕНТ ТРЕНИЯ. ТРЕНИЕ В ЖИДКОСТЯХ И ГАЗАХ. УЧЁТ И
ИСПОЛЬЗОВАНИЕ ТРЕНИЯ В БЫТУ И ТЕХНИКЕ.
1. Сила трения
сила, возникающая при
соприкосновении поверхностей двух тел и препятствующая взаимному перемещению. Она приложена к телу вдоль поверхности их соприкосновения и направлена против силы сдвигающей тело или относительной скорости перемещения.
Поверхность твердого тела даже хорошо отшлифованного, далеко неровная. На ней имеются микро выступы и впадины. При желании сдвинуть тела относительно друг друга выступы деформируются, и возникает
сила упругости, дающая силу трения. Также в местах близкого расположения молекул одного тела и молекул второго тела возникают силы притяжения между молекулами разных тел. Это тоже препятствует движению. Итак, силы трения – это силы электромагнитной природы.
Предположим, что у вас в комнате стоит шкаф. На него действуют силы тяжести и сила реакции опоры. Вы хотите передвинуть шкаф на другое место и прикладываете силу тяги, Fтяги, но шкаф остается на месте. Если шкаф остается на месте, то возникла сила равная, противоположная по направлению Fтяги. Это сила трения покоя Fтр. Вы прикладываете еще большую силу, но все безрезультатно. Значит, сила трения покоя тоже возросла. Сила трения покоя может, изменятся от 0 до некоторого максимального значения. Вы позвали на помощь родителей и сдвинули шкаф. Но все равно передвигать его тяжело. На тело действует сила трения скольжения. Она постоянна. Сила трения скольжения равна максимальной силе трения покоя Fтр= Fтр покоя max и как показывают опыты зависит от величины прижимающей силы и рода и качества поверхности. Fтр= μN, где N – cила реакции опоры μ – коэффициент трения-скольжения.
![]() Сила
трения-скольжения прямо пропорциональна силе нормального давления и не зависит
от площади соприкосновения. Для уменьшения трения применяется смазка. Между
соприкасающимися поверхностями помещают жидкость (масло). Сила жидкого трения
много меньше сухого трения. Например, находясь в лодке, вы легко можете,
оттолкнутся шестом от берега и двигаться, если лодка на берегу шест вам не
поможет.
Сила
трения-скольжения прямо пропорциональна силе нормального давления и не зависит
от площади соприкосновения. Для уменьшения трения применяется смазка. Между
соприкасающимися поверхностями помещают жидкость (масло). Сила жидкого трения
много меньше сухого трения. Например, находясь в лодке, вы легко можете,
оттолкнутся шестом от берега и двигаться, если лодка на берегу шест вам не
поможет.
Сила трения может быть как полезной, так и вредной. С помощью силы трения покоя мы ходим, автомобиль отталкивается колесами от дороги, но колеса автомобиля находятся на осях, подшипниках, трение которых нежелательно.
Пример: С каким максимальным ускорением может двигаться достаточно мощный автомобиль, если коэффициент трения скольжения равен 0,3
ДанАвтомобиль движется за счёт силы трения покоя.
![]() о: Максимальная сила
покоя равна силе трения =0, скольжения.
о: Максимальная сила
покоя равна силе трения =0, скольжения.
3 Силу трения скольжения найдём по формуле Fтр=N.
аmaxПри движении по горизонтальной поверхности сила
=? реакции опоры по модулю равна силе тяжести, а сила тяжести
равна FT=mG или FT=mg, отсюда Fтр=mg. Если колесо не проскальзывает (точки соприкосновения находятся в относительном покое), то Fтяги=Fтр, однако автомобиль движется с ускорением, поэтому Fтяги=ma, отсюда имеем ma = mg a = g. amax= 0,3x9,8 3м/с2.
Ответ: Автомобиль может двигаться с наибольшем ускорением 3м/с2
2. Сила сопротивления среды.
1. Сила гидростатического сопротивления.
(вывод формулы давления потока смотри в разделе «Потоки»)
![]() Поток
частиц оказывает давление на поверхность р=ρυ2(1+R), если
мы будем двигать поверхность в покоящейся среде частиц со скоростью υ, то
давление на поверхность будет таким же, для абсолютно упругого удара
р=2ρυ2. Возьмём клин с углом α, и будем перемещать
его со скоростью υ. Сила сопротивления давления будет равна Fc=F1+F2,
где F1- сила давления на верхнюю поверхность, а F2- сила
давления на нижнюю поверхность. F1=2Sρυ2cos2(90-α/2),
Fc=2F1cos(90-α/2), Fc=2x2Sρυ2cos2(90-α/2)xcos(90-α/2),
2Scos(90-α/2)=So, отсюда Fc=2Soρυ2cos2(90-α/2),
или Fc=2Soρυ2sin2α/2,
где So- площадь перпендикулярная потоку (скорости частиц).
Поток
частиц оказывает давление на поверхность р=ρυ2(1+R), если
мы будем двигать поверхность в покоящейся среде частиц со скоростью υ, то
давление на поверхность будет таким же, для абсолютно упругого удара
р=2ρυ2. Возьмём клин с углом α, и будем перемещать
его со скоростью υ. Сила сопротивления давления будет равна Fc=F1+F2,
где F1- сила давления на верхнюю поверхность, а F2- сила
давления на нижнюю поверхность. F1=2Sρυ2cos2(90-α/2),
Fc=2F1cos(90-α/2), Fc=2x2Sρυ2cos2(90-α/2)xcos(90-α/2),
2Scos(90-α/2)=So, отсюда Fc=2Soρυ2cos2(90-α/2),
или Fc=2Soρυ2sin2α/2,
где So- площадь перпендикулярная потоку (скорости частиц).
Анализируя формулу приходим к выводу, что при α=0о Fc=0 минимальна, а при α=180о Fc- максимальна. Отсюда ясно, почему такая форма носа у самолётов и кораблей. Для тела произвольной формы формула имеет вид
2
Fc CSo ![]() ρυ , где С – коэффициент сильно зависящий от 2
ρυ , где С – коэффициент сильно зависящий от 2
формы тела, его удобообтекаемости и свойств самой среды. Для шара С=0,4-0,2. Для каплеобразного тела С= 0,04.
2. Сила сопротивления вязкого трения.
В жидкости и в реальном газе молекулы взаимодействуют друг с другом, поэтому возникает так
называемое вязкое трение. Сила сопротивления вязкого трения пропорционально скорости движения тела в жидкости или газе. При больших скоростях существенную роль играет сила сопротивления давления, поэтому сила сопротивления пропорциональна квадрату скорости. При малых скоростях большую роль играет сила вязкого трения, которая пропорциональна скорости в первой степени. Fc=kυ
![]()
Пример1: Движение тел в восходящем потоке жидкости.
Задача о движении тел в восходящем потоке жидкости представляет значительный интерес при бурении нефтяных и газовых скважин, при выносе разбуренной породы на поверхность земли с помощью жидкости. Найдём наименьшую скорость восходящего потока (скорость витания), при которой порода будет подниматься на
поверхность земли. При равномерном движении породы сила тяжести равна сумме силы
2/2,
сопротивления и выталкивающей силы. FT FA FC 0 , FТ=mg, FA=ρжgV, FC=CSρжυ
![]()
![]() отсюда
FA-FT=FC, или Vg(ρт-ρж)=СSρжυ2/2,
поэтому
отсюда
FA-FT=FC, или Vg(ρт-ρж)=СSρжυ2/2,
поэтому
3 2 πd πd
υ
шара V
![]() , S
, S ![]() ,С=0,09,
,С=0,09,
6 4
.
(Е.З. Рабинович. «Гидравлика». М. Недра. 1980г.)
Пример2.
Падение тел в жидкости или газе.
При падении тела в жидкости или газе на него действуют сила тяжести, сила
сопротивления и сила Архимеда. Второй закон Ньютона выглядит так: ma FT FA FC.
Из трёх сил только одна является переменной. При увеличении скорости увеличивается сила сопротивления, а значит, уменьшается ускорение. Наконец ускорение становится равным нулю, и тело движется равномерно. FT=FA+FC. Если жидкость вязкая, то скорость установившегося движения невелика. Например, если стальной шарик падает в глицерине, то сила сопротивления пропорциональна скорости FC=6πηυr. (экспериментальная формула Стокса. Стр.320 Б.М. Яворский и А.А. Детлаф. «Справочник по физике» М.1963г). Скорость
2
![]() установившегося движения
найдём из равенства 6πηυr=mg-ρжgV
υ 2r g(ρ ρж) . В 9η
установившегося движения
найдём из равенства 6πηυr=mg-ρжgV
υ 2r g(ρ ρж) . В 9η
случае падения, например, капли воды в воздухе сила Архимеда незначительна, а скорость
ρ 2 2mg
![]()
![]() большая, поэтому mg CS гυ ,
откуда υ , где ρг-плотность
воздуха.
большая, поэтому mg CS гυ ,
откуда υ , где ρг-плотность
воздуха.
2 CSρг
Пример: Автомобиль движется со скоростью 72км/ч по ветру, скорость которого относительно земли равна 15м/с. Во сколько раз увеличится сила сопротивления воздуха при движении автомобиля с той же скоростью против ветра? Считать, что сила сопротивления пропорциональна квадрату относительной скорости.
![]() Дано: В первом случае
относительная скорость υА=20автомобиля
равна
Дано: В первом случае
относительная скорость υА=20автомобиля
равна
м/с υ1= υА-υВ, во втором υ2= υА+υВ, поэтому υВ=15СSρυA υB 2
м/с 2
F
![]() FC2 =? FC2C1
CSρυA2 υB 2 = υυAA υυBB 2 ;
FC2 =? FC2C1
CSρυA2 υB 2 = υυAA υυBB 2 ;
FC1
2
FC2 = ![]() (20 15)22 =49
(20 15)22 =49
FC1 20 15
Ответ: Сила сопротивления увеличилась в 49 раз. ( А.П. Рымкевич «Сборник задач по физике» М. Просвещение.1992г. №260)
ВОПРОСЫ
1. Что называется силой трения?
2. Куда направлена сила трения?
3. Чему равна сила трения покоя?
4. Чем обусловлена сила трения?
5. Какова природа силы трения?
6. По какой формуле находится сила трения скольжения?
7. Как уменьшить силу трения скольжения?
8. Что такое подшипник?
9. Какие подшипники вы знаете?
10. Какие вы знаете силы сопротивления среды?
11. Чем обусловлена сила гидростатического сопротивления?
12. Чем обусловлена сила вязкого трения?
ЗАДАЧИ
1. Сила, прижимающая деревянный ящик к полу, 500 Н. Чтобы его сдвинуть с места, потребовалось приложить силу 200 Н. Определите коэффициент трения покоя.
2. При помощи динамометра ученик перемещал деревянный брусок массой 600 г по горизонтально расположенной доске. Каков коэффициент трения, если динамометр показывал 0,6 Н?
3. Коэффициент трения между железной осью и бронзовым вкладышем подшипника без смазки равен 0,2. Сила, прижимающая вкладыш, 8000 Н. Какова в этом случае сила трения?
ДОМАШНЕЕ ЗАДАНИЕ 24
1. Сила, прижимающая деревянный ящик к полу, 400 Н. Чтобы его сдвинуть с места, потребовалось приложить силу 200 Н. Определите коэффициент трения покоя.
0,5
2. На столике в вагоне поезда лежит коробка конфет и яблоко. Почему в начале движения яблоко покатилось назад (относительно вагона), а коробка конфет осталась на месте?
3. При помощи динамометра ученик перемещал деревянный брусок массой 200 г по горизонтально расположенной доске. Каков коэффициент трения, если динамометр показывал 0,6 Н?
0,3
4. Почему коэффициент трения — безразмерная величина?
5. Коэффициент трения между железной осью и бронзовым вкладышем подшипника без смазки равен 0,18. Сила, прижимающая вкладыш, 10000 Н. Какова в этом случае сила трения?
1800 Н
6. Определить наименьшую скорость воды в скважине для подъёма частиц породы диаметром 5см и плотностью 2300 кг/м3. С =0,08
7. Определить установившуюся скорость падения града диаметром 1см.
29. ДВИЖЕНИЕ ТЕЛ ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ.
Пример: Автомобиль массой 5 тонн трогается с места с ускорением 0,6 м/с2. Найти силу тяги, если коэффициент трения 0,04.
![]() Дано Для простоты
приложим силы к одной m = точке, которая называется центром масс.
Дано Для простоты
приложим силы к одной m = точке, которая называется центром масс.
5т=5000 кг Запишем второй закон Ньютона в векторной a = 0,6 м/с2 форме:
μ = 0,04 Fтр Fт Fтяги N ma
Fтяги=?
Спроектируем на ось ОХ:
Fтяги- Fтр = ma, Fтр= μN Fтяги= ma+ μN
Сила реакции опоры неизвестна. Спроектируем на ось ОУ N-Fт=0 , так как ускорение направлено вдоль оси ОХ. N =mg, отсюда
Fтяги = ma+ μmg
Fтяги = m(a+ μg)=5000(0,6+0,04х9,8)=5000(Н)
Ответ: автомобиль будет двигаться с ускорением 0,6 м/с2, если сила тяги равна Fтяги =
5000Н
Пример: Мотоцикл, двигаясь по горизонтальной дороге, на повороте описывает дугу радиусом 100м. С какой максимальной скоростью может он ехать, если коэффициент трения резины о грунт 0,4?
Дано: Запишем второй закон Ньютона в векторной форме:
R=100м N FТ FТр ma μ=0,4
Спроектируем на ось ОХ:
υ=?
F = ma
тр , при движении по окружности Fтр – сила
![]() трения покоя.
Максимальная сила трения покоя равна F= μN, а центростремительное
ускорение направлено к центру окружности, для нахождения силы реакции опоры N
запи-
трения покоя.
Максимальная сила трения покоя равна F= μN, а центростремительное
ускорение направлено к центру окружности, для нахождения силы реакции опоры N
запи-
шем II закон Ньютона в проекциях на ось ОУ:
mυ2
N-FТ = 0
N = FТ, сила тяжести равна FТ=mG, или FТ=mg,
отсюда μmg= ![]() υ=
υ=
![]()
![]() R μgR υ= 0,49,8100 20м/с
R μgR υ= 0,49,8100 20м/с
Ответ: мотоцикл может двигаться без скольжения со скоростью не более 20 м/с.
Пример: Поезд массой 3000 т движется в низ под уклон равный 0,003. Коэффициент трения скольжения равен 0,008. С каким ускорением движется поезд, если сила тяги 300 кН?
![]() Дано: Запишем второй
закон Ньютона m=3000т в векторной форме
Дано: Запишем второй
закон Ньютона m=3000т в векторной форме
μ=0,008 тяги N ma
Fтяги=300кН
Спроектируем на ось tgα=0,003 а=?
- Fтр+FТsinα Fтр =N
Спроектируем на ось
N-Fтcosα=0, отсюда
Fтяги-mgcosα + mg sinα=ma
![]() Fтяги μmgcosα mgsinα a
Fтяги μmgcosα mgsinα a
m
а
![]()
0,05м/с2 cosα1
0,05м/с2 cosα1
Ответ: поезд движется под уклон с ускорением 0,05 м/с2
Пример: На шнуре перекинутым через неподвижный блок помещены грузы 0,3кг и 0,2 кг. С каким ускорением движется система? Какова сила натяжения шнура?
![]() Дано: Если нить нерастяжима.
Силы натяжения Т1 и Т2 m1=0,3кг равны.
Равны и ускорения, с которыми движутся тела. m2=0,2кг Запишем второй
закон Ньютона в векторной форме для а=? Т=? первого и второго тела:
Дано: Если нить нерастяжима.
Силы натяжения Т1 и Т2 m1=0,3кг равны.
Равны и ускорения, с которыми движутся тела. m2=0,2кг Запишем второй
закон Ньютона в векторной форме для а=? Т=? первого и второго тела:
F1 T1 m1a ; F2 T2 m2a
Спроектируем на ось ОУ:
1. T –FТ1= -m1a,
2. T-FТ2=m2a F1-m1a=F2+m2a FТ1-FТ2=(m1+m2)a
a mm11mm22g 0,30,30,20,29,8 1,96 м/с2
Т=m1g - m1a Т=m1(g - а) Т=0,3(9,8-2)=2,34 (Н)
Ответ: Тела движутся с ускорением 1,96м/с2. Сила натяжения равна 2,34 Н.
Пример: Груз, подвешенный на нити длиной l=60см, двигаясь равномерно, описывает окружность. Нить находится под углом 60о к плоскости окружности. Найти скорость груза.
![]() Дано: Запишем II
закон Ньютона TFT ma,
в проекциях l=0,6м Ox) Tcos=mυ2/R
(ускорение центростремительное)
Дано: Запишем II
закон Ньютона TFT ma,
в проекциях l=0,6м Ox) Tcos=mυ2/R
(ускорение центростремительное)
=60о
![]() υ=? Оy) Tsin-mg=0, отсюда
υ TR cosα , R=lcos m
υ=? Оy) Tsin-mg=0, отсюда
υ TR cosα , R=lcos m
gcos2α 9,80,60,52
![]() υ υ =1,3м/с sinα 0,87
υ υ =1,3м/с sinα 0,87
Ответ: Скорость груза равна 1,3 м/с.
ЗАДАЧИ
1. В шахту опускается бадья массой 0,3 т. Первые 0,1 мин она проходит 25 м. Найти силу натяжения каната, к которому подвешена бадья.
2. Груз массой 200 кг начали поднимать, когда он находился на высоте 4 м от поверхности земли. На какой высоте будет находиться груз через промежуток времени 6 с после начала подъема, если на тело со стороны каната действует постоянная сила 2000 Н?
3. Поезд массой 80 кг за 2 минуты увеличил скорость с 54 до 72 км/ч. Найти силу тяги, если коэффициент сопротивления движению 0,004.
4. Груз массой 250 кг лежит на дне кабины опускающегося лифта и давит на дно лифта с силой 2800 Н. Определить величину и направление ускорения лифта.
5. При помощи ленточного транспортера с углом наклона 20° поднимают вверх груз массой 50 кг. Какой должна быть сила трения, чтобы груз не скатывался по ленте?
6. Масса автомобиля с грузом 2 т, а скорость его движения 30 м/с. Чему будет равна сила давления автомобиля в верхней точке выпуклого моста, радиус кривизны которого 70 м?
7. Коэффициент трения скольжения между шинами автомобиля и асфальтом 0,5.
Определите радиус закругления на повороте, если автомобиль проходит его со скоростью 35 м/с.
ДОМАШНЕЕ ЗАДАНИЕ 24
1. В шахту опускается бадья массой 0,5 т. Первые 0,2 мин она проходит 35 м. Найти силу натяжения каната, к которому подвешена бадья.
4,65 кН
2. Груз массой 100 кг начали поднимать, когда он находился на высоте 2 м от поверхности земли. На какой высоте будет находиться груз через промежуток времени 4 с после начала подъема, если на тело со стороны каната действует постоянная сила 1080 Н? 10 м
3. Поезд массой 106 кг за 1 минуту увеличил скорость с 54 до 72 км/ч. Найти силу тяги, если коэффициент сопротивления движению 0,003.
80 кН
4. Груз массой 150 кг лежит на дне кабины опускающегося лифта и давит на дно лифта с силой 1800 Н. Определить величину и направление ускорения лифта.
2,2 м/с2 Лифт тормозится
5. При помощи ленточного транспортера с углом наклона 30° поднимают вверх груз массой 40 кг. Какой должна быть сила трения, чтобы груз не скатывался по ленте?
200 Н
6. Масса автомобиля с грузом 3 т, а скорость его движения 20 м/с. Чему будет равна сила давления автомобиля в верхней точке выпуклого моста, радиус кривизны которого 50 м?
6 кН
7. Коэффициент трения скольжения между шинами автомобиля и асфальтом 0,4.
Определите радиус закругления на повороте, если автомобиль проходит его со скоростью 28 м/с.
196
8. К бруску приложена сила, в результате чего он равномерно скользит по горизонтальному столу. Найти силу, если известны угол α, масса m и коэффициент трения μ между бруском и столом.
30. РАБОТА СИЛЫ ТЯЖЕСТИ
1.
![]() Тело движется вертикально вверх. Вычислим работу силы
тяжести
Тело движется вертикально вверх. Вычислим работу силы
тяжести
A=FтScos, угол между F и S равен 180о , сos180о = -1, A= -FтS, Fт=mg,
А= - mg(h2-h1). А = - (mgh2 – mgh1). Удобно U = mgh – принять за вид энергии, зависящей от положения тела. Из курса 7-го класса известно что это потенциальная энергия тела, поднятого над землёй.
А= - (U2 – U1).
Работа сил тяжести равна изменению потенциальной энергии с противоположным знаком. Если высоту, с которой бросили тело h1
принять равной нулю (нулевой уровень), то A= -mgh. Работа силы тяжести отрицательна.
2. Если тело движется вертикально вниз A=FтSсos, = 0о сos 0о =1 A=FтS, Fт=mg A=mgh.
При движении вниз работа силы тяжести положительна.
3. Движение тела по произвольной траектории
Тело массой m переместилось из точки А в точку В. Разобьем траекторию на отдельные участки. На участке АС работа силы тяжести A1=FтS1сos1 или A1=Fтh1, т.к. S1сos
1=h1. На участке СВ A2=FтS2сos 2, но S2сos 2=h2, значит A2=Fтh2. Полная работа силы тяжести А= А1+А2 или A =Fт (h1 +h2)
A =mgh
Вывод:
1. Работа силы тяжести не зависит от формы траектории, а зависит только от изменения высоты над поверхностью Земли, т.е. только от положения тела в пространстве. Силы, работа которых не зависит от формы траектории, а зависит от начального и конечного положения тела называются консервативными (потенциальными).
2. Работа силы тяжести по замкнутой траектории равна нулю.
И действительно выйдя из точки А и вернувшись в неё - тело, не изменило свою высоту
A =mg(h1 –h1 )=0
Если тело падает, то долетая до
некоторой высоты, оно имеет и скорость, и находится на некоторой высоте.
Значит, оно имеет и кинетическую энергию E ![]() и потенциальную U =
mgh . Полная
механическая энергия равна сумме кинетической и потенциальной энергий. W = E+U.
Полная механическая энергия в замкнутой системе является величиной постоянной.
Докажем это. Пусть тело брошено с некоторой высоты (h0 ≠ 0) без начальной скорости
υ0= 0. Энергия тела равна W = U = mgh0. Через
некоторое время оно будет иметь скорость υ = gt и окажется на высоте h
и потенциальную U =
mgh . Полная
механическая энергия равна сумме кинетической и потенциальной энергий. W = E+U.
Полная механическая энергия в замкнутой системе является величиной постоянной.
Докажем это. Пусть тело брошено с некоторой высоты (h0 ≠ 0) без начальной скорости
υ0= 0. Энергия тела равна W = U = mgh0. Через
некоторое время оно будет иметь скорость υ = gt и окажется на высоте h![]() Подставляя эти значения в выражение для полной энергии получим
Подставляя эти значения в выражение для полной энергии получим
![]() = mgh0, т.е. полная механическая энергия
не изменилась.
= mgh0, т.е. полная механическая энергия
не изменилась.
В замкнутой системе полная механическая энергия постоянна. Это закон сохранения механической энергии. Его можно записать в другом виде.
Е1 + U1 = E2 + U2
Сумма энергия до взаимодействия равна сумме энергий после взаимодействия.
Пример: Какой высоты достигнет тело, брошенное по вертикали вверх с начальной скоростью 50 м/с?
![]() Дано: Запишем закон
сохранения энергии U1+К1=U2+К2 υ=50h=? м/с h =0,
υ2=0, поэтому
Дано: Запишем закон
сохранения энергии U1+К1=U2+К2 υ=50h=? м/с h =0,
υ2=0, поэтому ![]() m2υ12 mgh h=
m2υ12 mgh h= ![]() 2υg12 ,
2υg12 ,
=125м/с
Тело, брошенное вертикально вверх со
скоростью 50м/с достигнет высоты 125м.
Вопросы
1. Чему равна работа силы тяжести?
2. Чему равна потенциальная энергия тела поднятого над землёй?
3. Зависит ли работа силы тяжести от траектории?
4. Как называются силы, работа которых по замкнутой траектории равна нулю?
5. Чему равна полная механическая энергия тела? 6. Сформулируйте закон сохранения энергии.
31. РАБОТА СИЛЫ УПРУГОСТИ
![]() Растянем пружину. При
равномерном движении наша сила должна равняться силе упругости пружины Fупр
=-кх, а сила внешняя Fвнеш = кх, при увеличении Х увеличивается
сила, поэтому работу вычислять простым умножением F на S нельзя. Схитрим,
построим график зависимости F(X), разделим Х на мелкие участки Δх , на
которых силу можно считать постоянной. Тогда элементарная работа будет
Растянем пружину. При
равномерном движении наша сила должна равняться силе упругости пружины Fупр
=-кх, а сила внешняя Fвнеш = кх, при увеличении Х увеличивается
сила, поэтому работу вычислять простым умножением F на S нельзя. Схитрим,
построим график зависимости F(X), разделим Х на мелкие участки Δх , на
которых силу можно считать постоянной. Тогда элементарная работа будет
равняться ΔА=F1Δх, т.е. площади маленького прямоугольника. Полная работа равна площади трапеции
![]() A
F1 F2 X2 X1; A
A
F1 F2 X2 X1; A ![]() k(X2
X1)(X2 X1) ; A
k(X2
X1)(X2 X1) ; A
![]() k(X22
X12 ) ; A kX22 kX12 .
k(X22
X12 ) ; A kX22 kX12 .
2 2 2 2 2
Мы нашли работу внешней силы. Работа силы упругости будет с противоположным
![]() знаком. A
kX2 22
kX212 ,
к
знаком. A
kX2 22
kX212 ,
к![]() 2х2
2х2![]() = U назовём потенциальной
энергией
= U назовём потенциальной
энергией
упругодеформированного тела (пружины) работа силы упругости равна изменению потенциальной энергии пружины взятой с минусом. Сила упругости пружины является консервативной в отличии от силы трения, которая относится к диссипативным силам, работа которых по замкнутой траектории не равна нулю.
kX12 kX22
![]() A
.
При растяжении работа силы упругости отрицательна, а при сжатии
A
.
При растяжении работа силы упругости отрицательна, а при сжатии
2 2
работа силы упругости положительна.
Пример: Сжатая пружина, жёсткость которой 10000Н/м, действует на прикреплённое к ней тело с силой 400Н. Какую работу совершит сила упругости пружины, если ей дать возможность восстановить первоначальную форму?
![]() Дано:
Работу
силы упругости найдём по формуле
Дано:
Работу
силы упругости найдём по формуле
Fk=10000=400H
H/м , где Х2=0, поэтому A
![]() kX212
kX212
А=?
Х – найдём из закона Гука. Fупр=кХ1, откуда
![]() Х1=Fупр/к; A
kFкупр22 Fупр2 A 10000
Х1=Fупр/к; A
kFкупр22 Fупр2 A 10000![]() 4002
16Дж
4002
16Дж
к
Ответ: Сила упругости пружины совершит работу 16 Дж.
Пример: По графику зависимости силы упругости от величины деформации определить работу силы упругости при удлинении пружины от 1 см до 3 см.
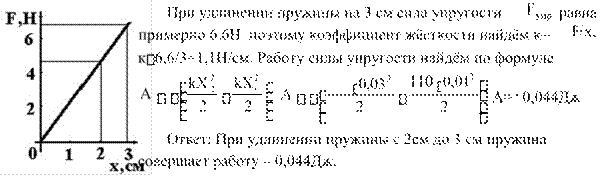 110
110
Пример: К пружинным весам подвешен груз. При этом, груз опустился и стрелка остановилась на цифре 3. Какова потенциальная энергия пружины, если шкала весов проградуирована в ньютонах, а расстояние между соседними делениями - 5мм
![]() Дано: Потенциальную
энергию пружины найдём по формуле
Дано: Потенциальную
энергию пружины найдём по формуле
N=3
ΔX=5мм . Х – величина деформации. Х =NΔX,
U=? где N-число делений, ΔX- расстояние между делениями.
![]() Коэффициент упругости
пружины найдём из закона к=F/X. U
FX2 FNΔN U
Коэффициент упругости
пружины найдём из закона к=F/X. U
FX2 FNΔN U ![]() 335103 =22,5х10-3
335103 =22,5х10-3
2X 2 2
Дж.
Ответ: Пружина имеет потенциальную энергию 22,5 Дж.
Пример: Пружина игрушечного пистолета жесткостью 800 Н/м сжали на 5 см. Какую скорость приобретет при выстреле пуля массой 20 г в горизонтальном направлении?
![]() При выстреле
энергия пружины полностью пули, которая изменяет свою
При выстреле
энергия пружины полностью пули, которая изменяет свою
кинетическую энергию. Запишем закон сохранения энергии. U1+К1=U2+К2, Х2=0, υ1=0, поэтому
2
Ответ: После выстрела пуля будет иметь скорость 10 м/с
ДОМАШНЕЕ ЗАДАНИЕ 24
1. К концу сжатия пружины детского пружинного пистолета на 3 см приложенная к ней сила была равна 20 Н. Найти потенциальную энергию сжатой пружины.
0,3 Дж
2. На пружине подвешен груз 300 кг, под действием которого она удлинилась на 6 см. Определите запас энергии деформированной пружины. 90 Дж
3. Определить запас энергии, который получает буферная пружина при сжатии ее на 5 см, если известно, что для сжатия пружины на 1 см нужно приложить силу 30 кН. 3,78 кДж
4. Определите величину деформации пружины при растяжении, если ее потенциальная энергия стала равной 1 Дж, а под действием силы 3 Н пружина удлиняется на 1 см.
8 см
5. Длина недеформированной пружины 15 см. В результате деформации ее длина удвоилась. Какой запас энергии получила пружина, если ее жесткость 400 Н/м?
4,5 Дж
32. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ
Закон сохранения механической энергии справедлив только для консервативных сил. Однако всегда присутствуют силы трения и сопротивления. Тогда закон сохранения механической энергии примет другой вид U1+K1=U2+K2+Aтр, Aтр – работа силы трения. kX2
Пусть пружина игрушечного пистолета
сжата и имеет энергию U ![]() .
.
2
При выстреле часть энергии пружины идет на увеличение кинетической энергии, а часть тратится на преодоление силы трения U1=K2+ Aтр , U1– затраченная энергия, энергия получаемая от пружины, К2 – полезная энергия пули. Ведь нам надо, чтобы пуля приобрела как можно большую скорость для полета. Отношение полезной работы (энергии) к затраченной работе (энергии) называется коэффициентом полезного действия – КПД, обозначается – η. Он выражается десятичной дробью или в процентах. КПД выстрела равен
Аполезная
η ![]() 100%. Пусть энергия пружины равна 5Дж, а пуля приобретает
кинетическую
100%. Пусть энергия пружины равна 5Дж, а пуля приобретает
кинетическую
Азатраченная
энергию 4.5Дж, тогда коэффициент полезного действия
выстрела равен η
![]()
0,9, или η
0,9, или η
![]() 100%
90%.
Закон сохранения энергии, тогда запишется
100%
90%.
Закон сохранения энергии, тогда запишется
ηАзатрач= Аполезн , или ηU1=К2
КПД ставиться перед затраченной энергией (работой).
Пример: найти КПД наклонной плоскости длиной 1м и высотой 0,6м, если коэффициент трения при движении по ней равен 0,1; как зависит КПД от угла наклона.
Дано: Мы поднимаем груз на
![]() S=1м высоту h, т.е.
действуем против h=0,6м силы тяжести совершая работу μ=0,1 А=mgh
– это полезная работа. η=? На самом деле нам надо двигать тело с
силой Fтяги, совершая работу затраченную
S=1м высоту h, т.е.
действуем против h=0,6м силы тяжести совершая работу μ=0,1 А=mgh
– это полезная работа. η=? На самом деле нам надо двигать тело с
силой Fтяги, совершая работу затраченную
Азатр= FтягиS.
Запишем второй закон Ньютона Fтяги Fтр N FT ma в проекциях на оси ох и оy:
Fтяги Fтр Fт sinα 0
N-Fтcosα0 Fтяги=mg(sinα+μcosα); Азатр= mg(sinα+μcosα)S, КПД-это
Aполез mgh
отношение полезной работы к затраченной. η ![]() η
η ![]() ;
sinα=h/S, Азатрач mg(sinα
μcosα)S
;
sinα=h/S, Азатрач mg(sinα
μcosα)S
откуда
η ![]() , если
вынести за скобку cosα, то η
, если
вынести за скобку cosα, то η
![]() , если sinα, тоη
, если sinα, тоη ![]()
η=0,6/(0,6+0,1х0,8)=0,88 sinα=h/S=0,6 α=37o cos37=0,8 Ответ: КПД наклонной плоскости 0,88 или 88 %
Пример: Насос с мотором мощностью 3кВт поднимает воду из колодца глубиной 20 м. Найдите массу воды, поднятую за 2 часа, если КПД= 70%.
![]()
![]() Дано:
Запишем закон сохранения энергии
Дано:
Запишем закон сохранения энергии
N=3000Вт Анасоса=Асилы тяжести
h=20м Коэффициент полезного действия, который t=2х3600с учитывает потери, поставим перед затраченной η=0,7 энергией (работой). Её можно узнать по
первоочередности. Сначала заработал насос, а потом m=?
вода стала подниматься, преодолевая силу тяжести.
ηАнасоса=Асила тяжести
ηNt=mgh m=ηNt/gh
m 77143кг
Ответ: за два часа насос поднимет 77143кг воды.
Пример: Самолёт летит прямолинейно и равномерно со скоростью 900км/ч. Какова сила сопротивления воздуха, если развиваемая двигателем мощность 1800кВт.
![]() Дано: При равномерном
движении сила тяги υ=250м/с равна силе сопротивления воздуха, поэтому
Дано: При равномерном
движении сила тяги υ=250м/с равна силе сопротивления воздуха, поэтому
N=1800000Вт N=Fυ, Fcопр=N/υ
Fсопр=? Fсопр=1800000/250=7200 (H).
Ответ: На самолёт действует сила сопротивления воздуха, равная 7200Н.
ВОПРОСЫ
1. Чему равна работа силы тяжести?
2. Какой природы сила тяжести?
3. Как называются силы, работа которых по замкнутой траектории равна нулю?
4. Как определить работу силы упругости?
5. Какой природы сила упругости?
6. Какие силы называются диссипативными?
ЗАДАЧИ
1. Какую работу совершает сила тяжести, действующая на тело массой 200г, при его падении с высоты 20км?
2. Какую работу совершает человек при подъёме груза массой 3кг на высоту 10м с ускорением 2м/с?
3. Какую работу нужно совершить для увеличения скорости поезда υ1=81км/час, до скорости υ2=120км/час? Масса поезда 12000т. Какова должна быть сила тяги локомотива, если это увеличение должно произойти на участке длиной 10000м?
4. Сжатая пружина, жёсткость которой 5000Н/м, действует на прикреплённое к ней тело с силой 300Н. Какую работу совершит сила упругости пружины, если ей дать возможность восстановить первоначальную форму?
5. К пружинным весам подвешен груз. При этом, груз опустился и стрелка остановилась на цифре 4. Какова потенциальная энергия пружины, если шкала весов проградуирована в ньютонах, а расстояние между соседними делениями - 5мм
6. Пружина игрушечного пистолета жесткостью 900 Н/м сжали на 4 см. Какую скорость приобретет при выстреле пуля массой 10 г в горизонтальном направлении?
7. Какой высоты достигнет тело, брошенное по вертикали вверх с начальной скоростью 90 м/с?
8. Найти КПД наклонной плоскости длиной 2м и высотой 1м, если коэффициент трения при движении по ней равен 0,1; как зависит КПД от угла наклона.
ДОМАШНЕЕ ЗАДАНИЕ 25
1. С плотины ежеминутно падает 18000 м3 воды с высоты 20 м. Какая при этом совершается работа? 36 108 Дж
2. Башенный кран поднимает в горизонтальном положении стальную балку длиной 5 м и сечением 100 см2 на высоту 12 м. Какую полезную работу совершает кран? 46 Дж
3. Автомобиль массой 10 т движется с выключенными двигателями под уклон по дороге, составляющей с горизонтом угол, равный 4°. Найти работу силы тяжести на пути 100м. 700 кДж
4. Груженая шахтная клеть массой 10 т поднимается с ускорением 0,5 м/с2. Определите работу по подъему клети за первые 10 с движения.
3 МДж.
33. ПОТЕНЦИАЛ. РАБОТА И РАЗНОСТЬ ПОТЕНЦИАЛОВ. ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ.
1. Потенциальная энергия тяготения. Потенциал.
Мы выяснили, что потенциальная энергия системы Земля и тело равна U=mgh, где h – расстояние от нулевого уровня потенциальной энергии, который мы можем выбрать сами.
M
Вспомним,
что напряженность гравитационного поля равна G
g γ ![]() R2 , тогда
R2 , тогда
U
γ ![]() MRm2 h
. Возьмем за нулевой уровень не поверхность земли, а центр Земли тогда h =
MRm2 h
. Возьмем за нулевой уровень не поверхность земли, а центр Земли тогда h =
![]() R
и U γ
mRM2R
γ mRM
, или
R
и U γ
mRM2R
γ mRM
, или
|
U γ M m R |
|
,
где U - потенциальная энергия гравитационного взаимодействия.
Знак минус указывает на то, что при увеличении R энергия стремится к нулю, то есть возрастает, ведь гравитационные силы являются силами притяжения.
Поместим в точку А гравитационного поля, созданного телом массой М тело небольшой m M
массы m1 – пробное тело. Оно обладает в этой точке
энергией U
γ ![]() 1 . Разделим обе
1 . Разделим обе
R
части уравнения на массу пробного тела m1. Внесем в точку А тело массой m2 и найдём отношение потенциальной энергии U к массе тела m.
U M
![]() γ
= m1 R
γ
= m1 R
![]() γ =
m2 R
γ =
m2 R
Отношение потенциальной энергии тела в точке А гравитационного поля к его массе величина постоянная и зависит от тела создающего поле и расстояния до выбранной точки.
U
Эта
величина, называется потенциалом гравитационного поля. ![]() (Дж/кг). Для грав m
(Дж/кг). Для грав m
сферических и точечных тел потенциал находится по формуле
M
γ ![]() , грав R
, грав R
где R – расстояние от центра тела, создающего гравитационное поле до точки, в которой
вычисляется потенциал.
Отсюда потенциальная энергия тела, находящегося в гравитационном поле равна
![]()
2. Работа и разность потенциалов
Работа силы тяжести равна А= - (U2-U1), или А = - (φграв2 – φграв1)m. A = (φграв1 – φграв2)m, A = Δφm, где Δφ – Разность потенциалов (не путать с изменением потенциала). Работа, совершаемая гравитационным полем при перемещении тела из одной точки поля в другую,
равна произведению массы тела на разность потенциалов начальной и конечной точки.
Как же связаны две характеристики гравитационного поля G – напряженность гравитационного поля (силовая характеристика) и Δφ разность потенциалов гравитационного поля (энергетическая характеристика гравитационного поля).
В однородном поле над поверхностью Земли, работу можно выразить через напряженность. А = FS, А=Gm(h1-h2) и через разность потенциалов А=m(φ1-φ2) приравнивая правые части, получим GΔh=Δφ,
G=Δφ/Δh,
где h расстояние вдоль силовой линии.
Пример: Определить потенциал гравитационного поля Земли на расстоянии 10000км от центра.
![]()
![]() Дано:
Потенциал поля найдём по формуле
Дано:
Потенциал поля найдём по формуле
R=107м M
24кг M=6х10грав γ R 24
=?
ãðàâ
6,67
10-11 ![]() 6 107 =40х106Дж/кг
6 107 =40х106Дж/кг
10
Ответ: Потенциал гравитационного поля Земли на расстоянии 10000км равен 40х106Дж.
Пример: Найти потенциал гравитационного поля образованного Землёй и Луной в точке удалённой от Земли на расстояние 5х108м и от Луны на расстояние 2х108м.
![]() Дано:
Потенциал в
точке А найдём по
Дано:
Потенциал в
точке А найдём по
R1=5x108м принципу суперпозиции. = З + Л , где З
R2=2x108м – потенциал от поля Земли, а Л – потенциал
MЗ=6х1024кг от поля Луны.
МЛ=7,4х1022кг MЗ MЛ
![]() =? = γ RЗ
γ RЛ ,
=? = γ RЗ
γ RЛ ,
-11 61024 7,41022
![]() = 6,67 10
8 2108
=
= 6,67 10
8 2108
=
510
= - 8,25х105Дж/кг.
Ответ: Потенциал гравитационного поля в точке А равен – 8,25х105Дж/кг
3. Потенциальная энергия электростатического взаимодействия. Потенциал электростатического поля.
Сравнивая закон всемирного тяготения
и закон Кулона, получим: Fграв γ ![]() m1R2m2 Fк k
m1R2m2 Fк k ![]() q1R2q2
q1R2q2
по аналогии введем понятие потенциальной энергии электростатического
взаимодействия
U γ ![]() m1
m2 U k
m1
m2 U k ![]() q1 q2 , или U
q1 q2 , или U
![]() q1 q2 грав R к R к 4πoR
q1 q2 грав R к R к 4πoR
Если заряды q1 и q2 имеют одинаковый заряд, то между ними действует сила отталкивания, а потенциальная энергия является положительной величиной. Если заряды q1 и q2 имеют разные знаки, то возникает сила притяжения и энергия будет отрицательной.
Для потенциала имеем
M Q
γ![]()
![]() грав R k 4εoR
грав R k 4εoR
U U
![]()
![]() . грав m k q Потенциал кулоновского
(электростатического) поля измеряется в Джоудь/Кулон или вольтах (В).
. грав m k q Потенциал кулоновского
(электростатического) поля измеряется в Джоудь/Кулон или вольтах (В).
Для работы
Аграв= mΔφграв АK=qΔφК
Для связи напряженности и разности потенциалов
Δφграв=Gh ΔφК=Еd,
где h и d соответственно расстояния вдоль силовой линии гравитационного и
электростатического (кулоновского) полей.
Напряжённость электростатического поля может быть выражена
![]() E
E
![]() Δk , E U где
Δφ разность потенциалов электрического поля равна напряжению
Δk , E U где
Δφ разность потенциалов электрического поля равна напряжению
d d ,
U и измеряется в вольтах, поэтому напряжённость электростатического поля имеет размерность В/м.
![]()
![]() 4.
Эквипотенциальные поверхности
4.
Эквипотенциальные поверхности
Точки с одинаковым потенциалом образуют поверхности равного потенциала или эквипотенциальные поверхности. Для точечных и сферических тел
эквипотенциальные поверхности представляют собой
концентрические сферы. Для однородного поля вблизи поверхности Земли эквипотенциальные поверхности являются плоскостями. Работа поля по перемещению тела по эквипотенциальной поверхности равна нулю т.к. разность потенциалов равна нулю.
![]() Эквипотенциальные поверхности поля тяготения Земли
– концентрические сферы. Спутник, движущийся вокруг Земли
по круговым орбитам, может оставаться на орбите сколь угодно долго, так как
работа не совершается, а значит и энергия не изменяется.
Эквипотенциальные поверхности поля тяготения Земли
– концентрические сферы. Спутник, движущийся вокруг Земли
по круговым орбитам, может оставаться на орбите сколь угодно долго, так как
работа не совершается, а значит и энергия не изменяется.
Электрическое поле заряженных пластин называется однородным, т,к, линии напряжённости являются
параллельными. Эквипотенциальные поверхности – параллельные плоскости. Для точечных или сферических тел эквипотенциальные поверхности являются концентрическими сферами.
Пример: Напряжённость электростатического поля равна 25В/м. Определить расстояние между эквипотенциальными поверхностями с потенциалами 4 и 6 вольт.
![]() Дано: Связь между
напряжённостью и потенциалом Е=25В/м электростатического поля определяется
формулой
Дано: Связь между
напряжённостью и потенциалом Е=25В/м электростатического поля определяется
формулой
1=4В Δk
2=6В E ![]() d , отсюда d=?
d , отсюда d=?
![]() d
Δk d 2
6 =
- 0,16м.
d
Δk d 2
6 =
- 0,16м.
E 25
Знак минус говорит о том, что d направлено против напряжённости электростатического поля, т.е. вдоль линии напряжённости потенциал убывает.
Ответ: Расстояние между эквипотенциальными поверхностями равно 0,16м.
Пример: Разность потенциалов между точками, лежащими на одной силовой линии на расстоянии 5 см друг от друга, равна 150 В. Найти напряжённость электростатического поля, если известно, что оно однородно.
Дано:=150 В Связь между
напряжённостью и потенциалом E
![]() Δk . Отсюда E
Δk . Отсюда E
![]() 150 d=0,05м d 0,05
150 d=0,05м d 0,05
Е=? = =3000В/м
Ответ: Напряжённость электростатического поля равна 3000В/м.
Пример: Определить потенциал электростатического поля, образованного сферическим зарядом 2х10-4Кл. в точке удалённой от центра тела на расстояние 6см.
![]() Дано: Q
Дано: Q
QR=0=2,06мx10-4
Кл Потенциал найдём по формулеk ![]() 4πoR
4πoR
=? k
![]() 4
3,14 128,8510-41012 0,06 =0,3x108В.
4
3,14 128,8510-41012 0,06 =0,3x108В.
Ответ: Потенциал равен 0,3х108 В.
ЗАДАЧИ
1. Определить потенциал гравитационного поля Земли на расстоянии 15000км от центра.
2. Найти потенциал гравитационного поля образованного Землёй и Луной в точке удалённой от Земли на расстояние 7х108м и от Луны на расстояние 2,5х108м.
3. Напряжённость электростатического поля равна 40В/м. Определить расстояние между эквипотенциальными поверхностями с потенциалами 6 и 10 вольт.
4. Разность потенциалов между точками, лежащими на одной силовой линии на расстоянии 15 см друг от друга, равна 300 В. Найти напряжённость электростатического поля, если известно, что оно однородно.
5. Определить потенциал электростатического поля, образованного сферическим зарядом 4,5х10-4Кл. в точке удалённой от центра тела на расстояние 1,5см.
ДОМАШНЕЕ ЗАДАНИЕ 27
1. Определить потенциал гравитационного поля Земли на расстоянии 25000км от центра. 2. Найти потенциал гравитационного поля образованного Землёй и Луной в точке удалённой от Земли на расстояние 3х108м и от Луны на расстояние 2х108м.
3. Электрические потенциалы двух изолированных проводников, находящихся в воздухе, равны 110В и – 110В. Какую работу совершит электрическое поле этих двух зарядов при переносе заряда 5•10-4 Кл с одного проводника на другой?
4. Заряд ядра атома цинка равен 4,8•10-18 Кл. Определить потенциал электростатического поля, созданного ядром атома цинка, на расстоянии 10 нм.
5. Какую скорость может сообщить электрону, находящемуся в состоянии покоя, ускоряющая разность потенциалов 1000 В? Масса электрона 9,1•10-31 кг.
6.
![]() Между двумя плоскими пластинами, к которым приложена
разность потенциалов 500 В, находится во взвешенном состоянии пылинка массой 10-7
г. Расстояние между пластинами 5 см. Определить электрический заряд пылинки.
Между двумя плоскими пластинами, к которым приложена
разность потенциалов 500 В, находится во взвешенном состоянии пылинка массой 10-7
г. Расстояние между пластинами 5 см. Определить электрический заряд пылинки.
7. В вершинах квадрата расположены заряды (в нКл): q1=+1, q2=-2 q3=+3 q4=-4. Найти потенциал электрического поля в центре квадрата. Диагональ квадрата равна 20см.
8. Определить работу электрических сил при перемещении заряда q =10-8
Кл из точки С в точку D, если q1=
5•10-6 Кл, q2= 2•10-6 Кл, ℓ = 0,4 м. АС
= 0,3 м.
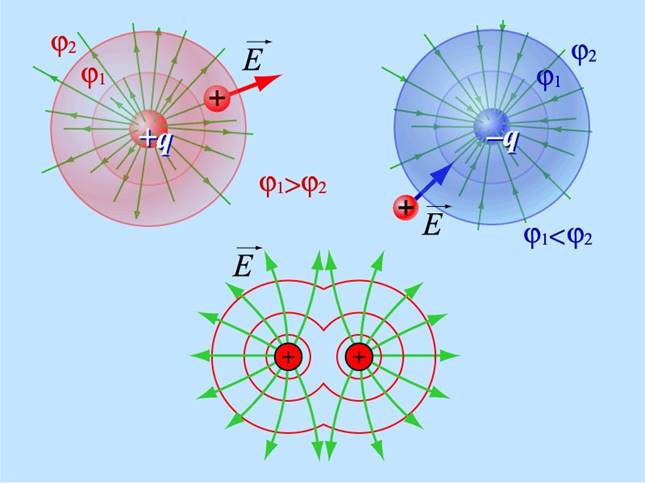
Электрическое поле точечных положительного, отрицательного и двух положительных зарядов.
34. ЁМКОСТЬ. ТЕПЛОЁМКОСТЬ. ЭЛЕКТРОЁМКОСТЬ. КОНДЕНСАТОРЫ.
Во многих случаях для определения количества жидкости в сосуде пользуются уровнем – специальной, тонкой, стеклянной трубкой. Если в сосуд наливать по объёмной единице жидкости, например по одному кубическому метру и на трубке отмечать их количество, то затем по высоте жидкости в трубке можно определить массу жидкости в сосуде. Δm=СΔh. ∆𝑚
![]() Величину С =
Величину С = ![]() - назовём ёмкостью сосуда С. Ёмкость
сосуда – величина, показывающая какое количество жидкости необходимо добавить в
сосуд для того, что бы её уровень поднялся на один метр. Для геометрически
правильных сосудов наша ёмкость численно равна площади основания умноженной на
плотность жидкости.
- назовём ёмкостью сосуда С. Ёмкость
сосуда – величина, показывающая какое количество жидкости необходимо добавить в
сосуд для того, что бы её уровень поднялся на один метр. Для геометрически
правильных сосудов наша ёмкость численно равна площади основания умноженной на
плотность жидкости.
В средние века учёные считали процесс теплопередачи перетеканием специальной жидкости (теплород) от одного тела к другому. Поэтому количество теплоты, требуемое на нагревание, находится по аналогичной формуле Q = CΔt, где Q – количество
теплоты, переданное от одного тела к другому, С – теплоёмкость тела (количество теплоты, необходимое для нагревания тела на один градус), Δt – количество градусов на которые нагрелось или остыло тело. Чаще пользуются удельной теплоёмкостью c – теплоёмкостью, которой обладает килограмм массы данного тела. Формула для расчёта количества теплоты выглядит так Q = cmΔt.
Возьмем два проводника произвольной формы, и будем перекачивать электроны с одного на другой с помощью электрофорной машины. При этом между проводниками возникает разность потенциалов, опыты показывают, что зависимость между зарядами и разностью потенциалов прямо пропорциональная q = СΔφ, С – назовем электроёмкостью системы проводников. Единица измерения - (Ф) фарада. Этот коэффициент зависит от геометрических размеров проводников, их взаимного расположения и пространства вокруг них. Для уединённого шара q = c(φ1-φ2). Потенциал на расстоянии r = ∞ равен нулю, поэтому q
c ![]() , или с=4πεεоr.
, или с=4πεεоr.
![]() Тела
с большой ёмкостью (объёмной для жидкости, тепловой и электрической) могут
использоваться как накопители данной величины. В засушливых районах строят
большие водохранилища, которые во время весеннего паводка заполняются водой, а
затем всё лето питают реки водой, спасая их от пересыхания. Другим примером
является «русская печь» - днём её топят, и она запасает тепло, а ночью
отдаёт тепло комнате. Электрический конденсатор
заряжается от сети (накапливает заряд), а затем может питать,
например лампу-вспышку фотоаппарата. Устройства с большими ёмкостями служат для
стабилизации данных величин. Например, водохранилище поддерживает
постоянный уровень воды в реке. Во время паводка оно задерживает
Тела
с большой ёмкостью (объёмной для жидкости, тепловой и электрической) могут
использоваться как накопители данной величины. В засушливых районах строят
большие водохранилища, которые во время весеннего паводка заполняются водой, а
затем всё лето питают реки водой, спасая их от пересыхания. Другим примером
является «русская печь» - днём её топят, и она запасает тепло, а ночью
отдаёт тепло комнате. Электрический конденсатор
заряжается от сети (накапливает заряд), а затем может питать,
например лампу-вспышку фотоаппарата. Устройства с большими ёмкостями служат для
стабилизации данных величин. Например, водохранилище поддерживает
постоянный уровень воды в реке. Во время паводка оно задерживает
часть воды, не давая подняться уровню реки, а во время
засухи - спасает от пересыхания. Динозавры – холоднокровные животные. Для
поддержания постоянной температуры им необходима была большая масса, т.е.
теплоёмкость. Днём огромный динозавр не успевал сильно нагреться, а ночью не
успевал сильно охладиться, таким образом, поддерживалась достаточно стабильная
температура. В электротехнике при пульсации напряжения параллельно потребителю
ставится конденсатор. При увеличении напряжения в сети часть тока идёт на
зарядку конденсатора, уменьшая ток нагрузки. При уменьшении напряжения
конденсатор подпитывает потребителя, тем самым, стабилизируя его ток. Из этого
следует, что конденсатор обладает энергией. Для конденсатора q = cΔφ,
а Δφ=U, где U – напряжение между пластинами, q – заряд пластины.
Напряжение в процессе разрядки конденсатора убывает прямо пропорционально
заряду. Среднее значение напряжения равно Uср =U/2. qU Работа по
перемещению заряда равна А=qUcр, или А= ![]() .
Работа по перемещению заряда – 2
.
Работа по перемещению заряда – 2
это энергия электрического поля конденсатора, поэтому
qU cU2 q2
W= ![]() , W=
, W= ![]() , W=
, W= ![]() .
.
2 2 2c
Конденсаторы как накопители электрических зарядов и энергии широко применяются в различных радиоэлектронных приборах. Они применяются для сглаживания пульсаций в выпрямителях переменного тока, для разделения постоянной и переменной составляющих тока, для накопления больших запасов электрической энергии.
![]() В
целях экономии материалов металлические электроды конденсаторов изготавливают
из тонкой фольги. В качестве изолирующей прокладки используется
парафинированная бумага, полистирол, слюда, керамика, воздух. Всё это помещают
в металлический или фарфоровый корпус. По типу диэлектрика
конденсаторы называются бумажными, слюдяными, и т.д. По характеру изменения
ёмкости они делятся на конденсаторы постоянной ёмкости, переменной
ёмкости и подстроечные. Электроёмкость обычно регулируется изменением взаимного
расположения пластин (площади пластин, находящихся друг против друга). Кроме
того, их делят на низко- и
высоковольтные, низко- и высокочастотные.
В
целях экономии материалов металлические электроды конденсаторов изготавливают
из тонкой фольги. В качестве изолирующей прокладки используется
парафинированная бумага, полистирол, слюда, керамика, воздух. Всё это помещают
в металлический или фарфоровый корпус. По типу диэлектрика
конденсаторы называются бумажными, слюдяными, и т.д. По характеру изменения
ёмкости они делятся на конденсаторы постоянной ёмкости, переменной
ёмкости и подстроечные. Электроёмкость обычно регулируется изменением взаимного
расположения пластин (площади пластин, находящихся друг против друга). Кроме
того, их делят на низко- и
высоковольтные, низко- и высокочастотные.
Вспомним как выводится формула энергии плоского конденсатора. W=ωV. Плотность энергии
равна![]()
|
|
|
|||
|
Где |
С = 0𝑆 𝜀𝜀 |
- ёмкость плоского конденсатора. |
|
|
𝑑
Пример: Конденсатор имеет электроёмкость 5пФ. Какой заряд находится на каждой из его обкладок, если напряжение между ними 1000В? Какова энергия электрического поля конденсатора?
Дано: Заряд конденсатора найдём по формуле q = сU
12 С=5х10- q =521012510001012100051029Кл. -6 Ф.
U=1000В. W= ![]() сU W=
сU W= ![]() =2,5х10 Дж. q=? 2 2
=2,5х10 Дж. q=? 2 2
Ответ: Заряд конденсатора равен 5х10-9Кл. Энергия конденсатора равна 2,5х10-6Дж.
Пример: Во сколько раз изменится энергия конденсатора, отсоединённого от источника тока, если пространство между его обкладками заполнить диэлектриком с диэлектрической проницаемостью равной 3?
![]() Дано:ε=3 W=q WW12 = qq22/2C/2C12 = CC12 =
Дано:ε=3 W=q WW12 = qq22/2C/2C12 = CC12 =
2/2C, заряд конденсатора не изменяется, поэтому
![]() W2 ? 1oS /d =1 W2 = 1
W2 ? 1oS /d =1 W2 = 1
W1 2oS /d 2 W1 3
Ответ: Энергия конденсатора уменьшится в 3 раза.
ЗАДАЧИ
1. При сообщении теплоприёмнику количества теплоты 8•105 Дж его температура поднялась на 10Со. Определить теплоёмкость устройства.
2. При сообщении электрическому конденсатору заряда 2•10-4 Кл разность потенциалов на его обкладках равна 2 В. Определить его ёмкость.
3. Теплоёмкость печи 2•105Дж/Со. Печь нагрета до80Со. Каждую секунду печь отдаёт 555,6 Дж тепла. Определить за какое время печь остынет до 20Со. Остывание считать равномерным.
4. Электроёмкость конденсатора 30 пФ. Он заряжен до напряжения 100В. Определить заряд конденсатора.
5. Во сколько раз изменится энергия конденсатора, отсоединённого от источника тока, если пространство между его обкладками заполнить диэлектриком с диэлектрической проницаемостью равной 12?
Вопросы:
1. Какая величина называется ёмкостью сосуда?
2. Что называется удельной теплоёмкостью тела?
3. Что называется электроёмкостью тела?
4. Чему равна электроёмкость шара?
5. Как находится энергия конденсатора?
6. Чему равна ёмкость плоского конденсатора?
ДОМАШНЕЕ ЗАДАНИЕ 28
1. Электроёмкость конденсатора 30 пФ. Он заряжен до напряжения 100В. Определить заряд конденсатора.
2. В паспорте конденсатора указано: «150 мкФ, 200 В». Какой наибольший допустимый электрический заряд можно сообщить данному конденсатору? 3·10-2 Кл
3. Конденсатор ёмкостью 2 мкФ заряжают до напряжения 110 В, затем отключив от сети, замыкают на конденсатор неизвестной ёмкости. Определить электрическую ёмкость второго конденсатора, если напряжение на нем стало 44 В. 3 мкФ
35. СОЕДИНЕНИЕ ЭЛЕКТРИЧЕСКИХ КОНДЕНСАТОРОВ.
Из курса физики 8го класса известно, что элементы электрической цепи могут быть соединены последовательно или параллельно.
![]() При
последовательном соединении общее напряжение равно сумме напряжений на
участках. U=U1+U2. Заряд конденсаторов одинаков,
т.к.
При
последовательном соединении общее напряжение равно сумме напряжений на
участках. U=U1+U2. Заряд конденсаторов одинаков,
т.к.
заряд пластин 2 и 3 в сумме должен быть равен нулю. q=q1=q2. Поэтому
![]() q q1 q2 → 1 1 1 . При последовательном
можно записать
q q1 q2 → 1 1 1 . При последовательном
можно записать
C C1 C2 C C1 C2
соединении конденсаторов можно пользоваться тремя уравнениями:
U=U1+U2
1/С=1/С1+1/С2 q=q1=q2
При параллельном соединении напряжения на потребителях одинаково U=U1=U2.Общий заряд равен сумме зарядов на каждом конденсаторе q=q1+q2. Заменяя заряды, через напряжение и ёмкость получим: СU=C1U+C2U → C=C1+C2.
U=U1=U2 C=C1+C2 q=q1+q2
При смешанном соединении расчёт схемы ведётся методом замещения: находятся участки с параллельным или последовательным соединениями заменяются одним конденсатором, затем процесс повторяется до полного расчёта общей ёмкости.
Пусть два конденсатора соединены параллельно. Ёмкость первого С1=20мкФ, а второго
С2=30мкФ. Напряжение 100В. Определить общий заряд батареи. Заряд конденсатора равен q=CU , q=q1+q2 → q=C1U+C2U. q=50∙10-6∙100=5∙10-3Кл=5мКл
ЗАДАЧИ
1.
![]() Определить электроёмкость батареи конденсаторов, если С1=С2=4нФ и С3=600пФ.
Определить электроёмкость батареи конденсаторов, если С1=С2=4нФ и С3=600пФ.
2. Определить электроёмкость батареи конденсаторов, если С1=0,2 мкФ, С2=0,5мкФ и С3=0,62мкФ.
3. Определить электроёмкость батареи конденсаторов, если С1=1мкФ, С2=4мкФ и С3=5мкФ. С4=1,8 мкФ, С5=4мкФ.
ДОМАШНЕЕ ЗАДАНИЕ 29
1. Определить электроёмкость батареи конденсаторов, если С1=С2=2нФ и С3=500пФ.
Отв. 444,4пФ.
2. Определить электроёмкость батареи конденсаторов, если С1=0,1 мкФ, С2=0,4мкФ и С3=0,52мкФ.
Отв. 0,6мкФ.
3. Определить электроёмкость батареи конденсаторов, если С1=2мкФ, С2=4мкФ и С3=1мкФ. С4=2 мкФ, С5=6мкФ.
Отв. 1,5мкФ.
4. Определить электрическую ёмкость батареи конденсаторов, если конденсаторы имеют одинаковую ёмкость, равную 0,6мкФ.
Отв. 0,24мкФ.
36. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РАВНОМЕРНО ДВИЖУЩЕЙСЯ ПО ОКРУЖНОСТИ. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ.
Пусть точка М равномерно движется по окружности со скоростью
υ. Координата х точки М изменяется по закону х = х0cos φ, если φ = ωt, где ω–угловая скорость, то x = x0cos ωt. Проекция вектора
скорости т.М на ось ox - υx = -υocos (π/2 - φ) или υx = -cos ( π/2 - ωt) или υx = -υo sin ωt (тригонометрические функции дополнительного аргумента). Точка М движется с центростремительным ускорением, проекция которого на ось ох равна ax = - a0 cos ωt. Уравнения движения:
![]()
![]() x = x
cos ωt, y = y0 sin
ωt, υx
= -υ0 sin ωt, υy =
υ0 cos
ωt, ax
= - a0 cos ωt ay = - a0 sin
ωt..
x = x
cos ωt, y = y0 sin
ωt, υx
= -υ0 sin ωt, υy =
υ0 cos
ωt, ax
= - a0 cos ωt ay = - a0 sin
ωt..
Выразим линейную скорость и центробежное ускорение через угловую скорость: υо= ωR, aо = υо2 /R = ω2R, где R = xо, тогда x = xоcos ωt, υx = -ωxоsin ωt, ax = - ω2xоcos ωt,
но тогда уравнения движения т.М в проекциях на ось ох запишутся:
x = xоcos ωt или в общем случае x = xо cos(ωt + φо) υх = -ωxо sin ωt υх = - ωxо sin(ωt + φо) aх = - ω2x0 cos ωt aх = - ω2xо cos(ωt + φо) где φ0 – значение угла в момент времени t=0.
Аналогично для oy. Проекция точки М на ось ох совершает колебательное движение.
Колебания
Среди всевозможных движений большее распространение имеют колебания. Колебания совершают электроны и молекулы, детали машин. Благодаря колебаниям мы видим и слышим.
Механическими колебаниями называют периодически повторяющиеся движения.
механические колебания подразделяются на
• свободные или собственные колебания - происходящие без переменного внешнего воздействия и поступления энергии извне (маятник, тело подвешенное на пружине);
• ![]() периодические
- при которых значения координаты, скорости и ускорения циклически повторяются
через определённые промежутки времени (если это условие не выполняется, то
колебания апериодические);
периодические
- при которых значения координаты, скорости и ускорения циклически повторяются
через определённые промежутки времени (если это условие не выполняется, то
колебания апериодические);
• вынужденные - вызываемые и поддерживаемые переменной во времени внешней силой;
• параметрические - вызываемые изменением во времени динамических параметров системы ( жесткости, массы или момента инерции, демпфирования и др.);
• автоколебания - стационарные колебания, возбуждаемые и поддерживаемые за счет энергии поступающей от источника не колебательного характера, в которой поступление энергии регулируется движением самой системы;
Характеристики колебательного движения:
А, х0, хmax – амплитуда колебаний – наибольшее смещение [метр] ω – круговая или циклическая частота [рад/сек] T – время одного полного колебания [сек]
𝑡
Если
за время t тело совершает N колебаний, то ![]() ν – частота -
число колебаний в секунду [Гц] - герц ν = 1/ ω = 2π /T ω
= 2πν T = 2π/ω (ωt +
φо) – фаза колебаний, φо – начальная фаза.
ν – частота -
число колебаний в секунду [Гц] - герц ν = 1/ ω = 2π /T ω
= 2πν T = 2π/ω (ωt +
φо) – фаза колебаний, φо – начальная фаза.
Если закон движения материальной точки выражается в виде синусоидальной функции зависимости координаты от времени, то говорят, что эта точка совершает гармонические колебания. Проекция точки М, равномерно движущейся по окружности на ось х совершает гармонические колебания т.к. уравнения движения:
x = Аcos(ωt + φо) υ = - ωxо sin(ωt + φо) a = - ω2А cos(ωt + φо)
Графики смещения, скорости и ускорения
![]() Как
видно из графиков скорость отличается по фазе от смещения на π/2, а
ускорение на π.
Как
видно из графиков скорость отличается по фазе от смещения на π/2, а
ускорение на π.
Пример: Дано уравнение колебаний материальной точки x = 0.2 sin (2πt +π) определить параметры колебаний
x = 0.2 sin (2πt +π);
x = A sin (ωt + φ);
A = 0.2; ω = 2 π; φ = π; T = 2π /ω = 2π/2π = 1 c; ν = 1/T = 1Гц.
ВОПРОСЫ
1. Какое движение называется механическими колебаниями?
2. Какие колебания называются свободными?
3. Какие колебания называются вынужденными?
4. Какие колебания называются периодическими?
5. Какое движение называется вынужденными колебаниями?
6. Что такое автоколебания?
7. Что такое амплитуда колебаний?
8. Что называется периодом колебаний?
9. Что такое частота колебаний?
10. Как связаны период и частота колебаний?
11. Что такое фаза колебаний?
12. Какие колебания называются гармоническими?
ДОМАШНЕЕ ЗАДАНИЕ 30
1. Материальная точка за 3 мин совершила 300 колебаний. Определить период и частоту колебаний.
2. Материальная точка колеблется с частотой ν=10 кГц. Определить период и число колебаний в минуту.
3. Определить смещение от положения равновесия в моменты t1=0, t2=T/12, t3=T/4, t4=T/2 материальной точки, совершающей гармонические колебания. Начальная фаза колебаний равна нулю, амплитуда колебаний равна 2м.
4. Записать уравнения гармонических колебаний при следующих параметрах: 1) А =10,0 см, φо==π/4, ω=2π; 2) А=5,0 см, φо= л/2, Т=2,0 с; 3) А =4,0 см, φо=π, ν=2,0 Гц.
5. Материальная точка совершает гармонические колебания по закону х=2sin[(π/4)t+π], где х выражено в сантиметрах, t — в секундах. Определить амплитуду колебаний, начальную фазу, период колебаний.
6. Записать уравнение гармонических колебаний при следующих параметрах: A==5,0·10-2 м, φо==0. Длина нити математического маятника 40м. Определить частоту колебаний, циклическую частоту.
7. Материальная точка совершает гармонические колебания по закону х=4sin[(π/6)t+π/2], где х выражено в сантиметрах, t — в секундах. Определить амплитуду колебаний, начальную фазу, период колебаний.
8.
![]() Тело массой 0,2 кг совершает гармонические колебания по
закону x=0,10sin(628t+л/3). Определить амплитуду смещения, начальную
фазу, частоту колебаний, период колебаний, амплитуду скорости, максимальную
кинетическую энергию, максимальную потенциальную энергию, полную энергию.
Тело массой 0,2 кг совершает гармонические колебания по
закону x=0,10sin(628t+л/3). Определить амплитуду смещения, начальную
фазу, частоту колебаний, период колебаний, амплитуду скорости, максимальную
кинетическую энергию, максимальную потенциальную энергию, полную энергию.
9. По графику зависимости смещения от времени определить амплитуду колебаний, период, частоту, начальную фазу.
37. Вынужденные гармонические колебания.
Колебания тела, которые создаются внешней, периодической силой, называются вынужденными колебаниями. Рассмотрим движение кривошипно–шатунного механизма. При равномерном вращении кривошипа r движение через шатун АМ= передается точке М поршня.
Поршень совершает колебания. т.А движется из т хо. Проекция т. А на ОХ совершает гармонические колебания х=rcosωt. Координата тМ складывается из отрезков ОХ+ХМ, ОХ=rcosφ,
![]()
![]() ХМ
= r
sin .
Уравнение движения т М
x =r cosωt + 2 r2 sin2,
Если
ХМ
= r
sin .
Уравнение движения т М
x =r cosωt + 2 r2 sin2,
Если
>>r, то x = r cosωt +
Если систему координат перенести в центр между крайними положениями т М, то уравнение в новых координатах будет выглядеть х = r cosωt или х = А cosωt, где А – амплитуда колебаний, ω – циклическая частота, т.е. движение поршня, является гармоническими колебаниями, т.е., подчиняющимися законам синуса или косинуса. Пример: дано уравнение колебаний материальной точки x = 0,2 sin (2πt+π)
определить параметры колебаний.
х = 0,2 sin (2πt+π) x = Аsin (ωt+ φ0), φ0 – начальная фаза.
А=0,2; ω=2π; φ0= π; Т=2π/ω=2π/2π=1 с.
ν =1/T= 1 Гц.
Уравнения движения проекции т А на ось ОХ:
x = А cosωt υх = -ωА sinωt aх= -ω2А cosωt
Поршень М движется синхронно с проекцией точки А на ось ОХ, с ускорением a= -ω2А cosωt, значит на него действует со стороны шатуна сила Fх= maх, Fх= - mω2А cosωt движение поршня будут являться вынужденными колебаниями. Колебания происходят под действием внешней периодической силы. С какой скоростью мы будем вращать кривошип – с такой круговой частотой будут происходить колебания поршня.
Сила F= -kx, где k=mω2, x = А cosωt, называется квазиупругой, подобной упругой силе.
Сила направлена против смещения и к центру равновесия расположенному посередине между крайними точками смещения.
Итак, F= -kx; k=mω2 ; x = cosωt; υ = -ωА sinωt; a= -ω2А cosωt. ω2=к/m
ВОПРОСЫ
1. Что такое механические колебания?
2. Что называют свободными колебаниями?
3. Что называется периодом колебаний?
4. Что такое частота колебаний?
5. Что такое амплитуда колебаний?
6. Что такое фаза?
7. Что называют вынужденными колебаниями?
8. Что такое квазиупругая сила?
9. Чему равна циклическая частота квазиупругой силы?
которые
значение каждой точки x, равно алгебраической сумме x1 и x2.
Рассмотрим два частных случая
1. Оба колебания имеют одинаковый период, и разность фаз равна нулю. В этом случае колебания усиливают друг друга.
2. Пусть оба колебания имеют одинаковый период и разность фаз 180˚. Результирующее колебание равно разности x= x 1 –x2 . Колебания гасят друг друга, а если амплитуды их одинаковы, результирующее колебание равно нулю.
Если функции имеют одинаковую циклическую частоту, то можно представить их и их сумму векторами. Например, функция x=А1cosωt – чёрный вектор, функция x=А2cos(ωt+φ2) – красный вектор. Теперь определим геометрически (циркулем) начальную фазу и амплитуду (линейкой), а затем запишем новую функцию x=А3cos(ωt+φ3) – коричневый вектор.
Вопросы:
1. ![]() Как геометрически
складываются колебания?
Как геометрически
складываются колебания?
2. Какие частные случаи необходимо рассмотреть?
3. Как складываются геометрически колебания одинаковой частоты?
39. СВОБОДНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ.
![]() Пружинный
маятник представляет собой груз массой m укрепленный на пружине, коэффициент
упругости которой k.
Пружинный
маятник представляет собой груз массой m укрепленный на пружине, коэффициент
упругости которой k.
![]() Если отклонить груз
от положения равновесия вправо, то на него будет действовать сила упругости,
направленная против смещения x к центру равновесия. Груз начнет двигаться,
энергия пружины Wпmax=kxо2/2 будет
превращаться в кинетическую энергию тела и в точке равновесия будет равна Екmax=mυ2max/2.
По инерции тело будет двигаться вправо до остановки, в которой его энергия
опять станет равной Wпmax=kxо2/2. При
отсутствии трения полная энергия остаётся постоянной и равняется
Если отклонить груз
от положения равновесия вправо, то на него будет действовать сила упругости,
направленная против смещения x к центру равновесия. Груз начнет двигаться,
энергия пружины Wпmax=kxо2/2 будет
превращаться в кинетическую энергию тела и в точке равновесия будет равна Екmax=mυ2max/2.
По инерции тело будет двигаться вправо до остановки, в которой его энергия
опять станет равной Wпmax=kxо2/2. При
отсутствии трения полная энергия остаётся постоянной и равняется
W=Wп+Ек
![]() 2 2 2 2
2 2 2 2
Если не принимать во внимание постепенное затухание колебаний, то они будут гармоническими: ведь исходя из уравнения движения для вынужденных колебаний, движение происходит под действием силы F= -kx , которая направлена к центру равновесия, значит, x = А cosωt, υ = -ωА sinωt, a= -ω2А cosωt, k=mω2
, период пружинного маятника равен
![]() T= 2π m
T= 2π m
k Рассмотрим движение тела, подвешенного на длинной нити (математический маятник) При небольших отклонениях, движение шарика можно считать гармоническими колебаниями. Из подобия треугольников ОАВ и треугольника, образованного силами Fв и Fт, где Fт – сила тяжести, а Fв – возвращающая сила, равная сумме силы тяжести и силы упругости нити, следует.
Fт/Fв=/AB - АВ приближенно равно x
mg
Fв = - ![]() x ,
или Fв = -kx, и направлена к центру равновесия, где k=mg/ℓ, но тогда
x ,
или Fв = -kx, и направлена к центру равновесия, где k=mg/ℓ, но тогда
x=Аcosωt,
υ= -ωАsinωt, a= -ω2Аcosωt,
![]()
![]()
![]() k mg 2 ω=
ω=,
период математического маятника равенΤ π. m m g
k mg 2 ω=
ω=,
период математического маятника равенΤ π. m m g
ВОПРОСЫ
1. Что представляет собой пружинный маятник?
2. Чему равна первоначальная энергия пружины?
3. Чему равна энергия тела при прохождении положения равновесия?
4. Чему равна полная энергия тела в любой момент времени?
5. Чему равен период колебаний пружинного маятника?
6. Что представляет собой математический маятник?
7. Чему равен период колебаний математического маятника?
ЗАДАЧИ
1. Частота колебаний 20000 Гц. Определить период колебания.
5 10-5 c 2. Период колебания 10-2 с. Определить частоту колебаний. 100 Гц
3. Сколько колебаний совершит материальная точка за 5 с при частоте колебаний 440 Гц?
2200
4. Определить период колебаний материальной точки, совершившей 50 полных колебаний за 20 с. 0,4 с
5. Материальная точка за 1 мин совершила 300 колебаний. Определить период колебаний и частоту. 0,2 с 5 Гц
6. Найти период и частоту колебаний математического маятника, длина нити которого равна 0,634 м.
1,72 с 0,582 Гц
7. Пружина под действием прикрепленного к ней груза массой 5 кг совершает 45 колебаний в минуту. Найти коэффициент жесткости пружины. 1,08 кН/м
8. Найти массу груза, который на пружине жесткостью 250 Н/м делает 20 колебаний за10 с.
4 кг
9. Как изменится период колебаний математического маятника, если его длину увеличить в 4 раза?
Увеличится в 2 раза
ДОМАШНЕЕ ЗАДАНИЕ 31
1. Материальная точка колеблется с частотой 10 кГц. Определить период колебаний и число колебаний в минуту.
10-4 с 6 105 мин-1
2. Грузик, колеблющийся на пружине, за 8 с совершил 32 колебания. Найти период и частоту колебаний.
0,25 с 4 Гц
3. Ускорение свободного падения на поверхности Луны 1,6 м/с2. Какой длины должен быть математический маятник, чтобы его период колебания на Луне был равен 1 с ?
4 см
4. Частота колебаний крыльев комара 600 Гц, а период колебаний крыльев шмеля 5 мс.
Какое из насекомых и насколько больше, сделает при полете взмахов крыльями за 1 мин?
Комар сделает на 240000 взмахов больше
5. Тело массой 0,2 кг подвешено на пружине, жесткость которой 2 кН/м. Определить частоту свободных колебаний этого тела на пружине. 16 Гц
Декартовы координаты частицы изменяются следующим образом: х=Аcosωt, y=Asinωt, z=Aωt, где А и ω положительные константы. Какой путь пройдёт точка за время to?
Автоколебания
![]() Для того, чтобы свободные колебания были незатухающими
необходимо пополнять энергию, потраченную на
трение. Примером механических автоколебаний являются часы.
Любая автоколебательная система состоит из
колебательной системы, в которой возникают свободные
колебания, постоянной энергии для компенсации
Для того, чтобы свободные колебания были незатухающими
необходимо пополнять энергию, потраченную на
трение. Примером механических автоколебаний являются часы.
Любая автоколебательная система состоит из
колебательной системы, в которой возникают свободные
колебания, постоянной энергии для компенсации
энергетических потерь и устройства обратной связи, которая передаёт эту энергию колебательной системе в нужный
В часах ходиках потенциальная энергия гири с помощью анкерного устройства передаётся маятнику, компенсируя потери энергии на трение.
40. УСЛОВИЯ РАВНОВЕСИЯ ТВЁРДОГО ТЕЛА. ВИДЫ РАВНОВЕСИЯ. ПРИНЦИП МИНИМУМА ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ. МОМЕНТ СИЛЫ.
УСЛОВИЯ РАВНОВЕСИЯ ТЕЛА, ИМЕЮЩЕГО ОСЬ ВРАЩЕНИЯ.
Статика.
![]() Равновесие
тела при отсутствии вращения.
Равновесие
тела при отсутствии вращения.
Равновесие тела – это движение с постоянной скоростью или со скоростью равной нулю. Это возможно, если равнодействующая всех сил, действующих на тело равна нулю. I закон Ньютона. Тело может двигаться поступательно, когда все точки его движутся по взаимно параллельным траекториям, а также может совершать вращательное движения, когда точки тела движутся по окружности.
![]() Пусть тело не может
совершать вращательное движение. Например, тело (санки) находятся на наклонной
плоскости. Чтобы оно двигалась равномерно и прямолинейно (по первому закону
Ньютона) необходимо, чтобы равнодействующая сил, действующих на тело, равнялась
R=0, но тогда и ее проекции на любую ось равны 0, т.е. равны нулю суммы
проекций всех сил. И условие равновесия можно записать так: ∑ Fx,=0
∑Fy,=0 ∑Fz=0 – условие равновесия
Пусть тело не может
совершать вращательное движение. Например, тело (санки) находятся на наклонной
плоскости. Чтобы оно двигалась равномерно и прямолинейно (по первому закону
Ньютона) необходимо, чтобы равнодействующая сил, действующих на тело, равнялась
R=0, но тогда и ее проекции на любую ось равны 0, т.е. равны нулю суммы
проекций всех сил. И условие равновесия можно записать так: ∑ Fx,=0
∑Fy,=0 ∑Fz=0 – условие равновесия
где Fx, Fy, Fz– проекции силы F на оси координат ох, оy, oz. Если
силы действуют на тело лишь в одной плоскости, то достаточно двух условий равновесия ∑ Fx,=0 ∑Fy,=0 Выясним условие покоя для тела, находящегося на наклонной плоскости. Спроектируем сумму всех сил на ОХ и ОУ и приравняем к нулю.
FTsin-Fтр=0
![]() FTsin-N=0
FTsin-N=0
N-FTcos=0
N=FTcos
FTsin
= FTcos. Разделим обе
части уравнения на FTcos,
получим ![]() μ
0, или
tg = .
μ
0, или
tg = .
Тело находится в покое при отсутствии вращения на наклонной плоскости, если
tg
К кронштейну ВАС подвешиваем груз массой m. Найти усилие в стержнях ВА и АС.
Так как тело находится в покое то Fт = Т = mg. Запишем условие равновесия для узла
mg mg
![]() 1
1 ![]() . F2=
. F2=
![]() sinα
F2=mgtgα cosα cosα
sinα
F2=mgtgα cosα cosα
Равновесия можно разделить на три вида:
1. Безразличное.
2. Неустойчивое
3. Устойчивое
При безразличном равновесии при выводе тела из равновесии оно остаётся в равновесии, но в новом положении. При неустойчивом равновесии при выводе тела из равновесия тело не возвращается в прежнее состояние, движется от точки равновесия, т.к. равнодействующая направлена от точки равновесия. При устойчивом
равновесии, при выводе тела из положения равновесия тело возвращается в прежнее состояние т.к. равнодействующая направлена к положению равновесия. Из рисунка видно, что тело стремится к положению, когда его потенциальная энергия (W=mgh ) минимальна.
Равновесие тела при наличии оси вращения. Если на тело действуют две равные параллельные силы, направленные в противоположные стороны и не проходящие через одну точку, то такое тело не будет находиться в равновесии.
![]() Возьмем
два тела на жестком невесомом стержне и закрепим их на оси так, чтобы ось
проходила через стержень, и он мог легко поворачиваться. В общем случае
равновесие наступит тогда, когда,
Возьмем
два тела на жестком невесомом стержне и закрепим их на оси так, чтобы ось
проходила через стержень, и он мог легко поворачиваться. В общем случае
равновесие наступит тогда, когда,
произведение F1r1, будет равно F2r2. Моментом силы F называется
вектор М , направленный вдоль оси вращения и ориентированный по
правилу правого винта относительно вектора силы. Модуль момента силы равен М=Frsinα=Fd, где d – плечо силы. Произведение силы на кротчайшее расстояние до оси – плечо силы, называется моментом силы МFxr (Нм). За положительное значение момента силы возьмем направление, при котором система будет вращаться против часовой
![]() стрелки.
Тогда условие равновесия запишется М1-М2=0 или ∑ М=0
стрелки.
Тогда условие равновесия запишется М1-М2=0 или ∑ М=0
Это условие называется правилом моментов. Тело, система тел, имеющие неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех сил, действующих на тело, систему тел, относительно оси вращения
равна нулю.
Моменты, вращающие против часовой стрелки – положительные, а по часовой - отрицательные. Для общего случая в трёхмерном пространстве условия равновесия выглядят так:
Fx=0, Fy=0, Fz=0, ∑ М=0.

Пример: Труба массой 100 кг лежит на двух опорах. Длина трубы 6 м, одна опора находится у конца трубы, вторая – на расстоянии 1 м от второго конца трубы. Определить силы реакции опор.
![]() Дано:
На трубу действуют сила тяжести, проходящая L=6м через центр тяжести 0 и силы
реакции опор N1 и N2. L3=1м Так как труба
находится в покое, запишем условия m=100кг равновесия.
Дано:
На трубу действуют сила тяжести, проходящая L=6м через центр тяжести 0 и силы
реакции опор N1 и N2. L3=1м Так как труба
находится в покое, запишем условия m=100кг равновесия.
NN12==?? 1) FT N1 N2 0
2) M=0, В проекциях на ось ОY имеем
![]()
![]()
![]()
![]() -FT+N1+N2=0
FT=N1+N2 На основании правила моментов запишем
равенство, выбрав за ось вращения центр масс. N1l1+N2l2=0
(момент силы тяжести относительно т.0 равен нулю, т.к. её плечо равно
нулю). FT=N1+N2 Решаем эту
систему уравнений:
-FT+N1+N2=0
FT=N1+N2 На основании правила моментов запишем
равенство, выбрав за ось вращения центр масс. N1l1+N2l2=0
(момент силы тяжести относительно т.0 равен нулю, т.к. её плечо равно
нулю). FT=N1+N2 Решаем эту
систему уравнений:
N1l1=N2l2 N1
![]() N2 2 ,
FT N2 2
N2 N212 1
; N2 2FT1
mg2 1,
N2 2 ,
FT N2 2
N2 N212 1
; N2 2FT1
mg2 1,
1 1 по условию l1=3м, l2=2м N2=100x9,8x3/5=600H N1=600x2/3=400H Ответ: Сила реакции опоры N1=400H, а сила реакции опоры N2=600H.
ЗАДАЧИ
1. Два человека одинакового роста держат на плечах за концы трубу длиной 4 м и массой 10 кг. На расстоянии 1 м от первого человека к трубе подвешен груз массой 100 кг.
Определить силы, с которыми труба действует на плечи первого и второго человека.
2.
![]() Балка длиной 6м и массой 100кг расположена горизонтально и
покоится на двух опорах, АМ=2м, МN=2м, NB=2м. На расстоянии 1м от левого конца
балки подвешен груз массой 40 кг. Определить реакции опоры.
Балка длиной 6м и массой 100кг расположена горизонтально и
покоится на двух опорах, АМ=2м, МN=2м, NB=2м. На расстоянии 1м от левого конца
балки подвешен груз массой 40 кг. Определить реакции опоры.
3. Однородный стержень массой 0,2кг укреплён одним концом в шарнире и удерживается в равновесии с помощью нити прикреплённой к другому её концу угол α=45о. Найти силу натяжения нити и реакцию опоры шарнира.
4. При помощи ленточного транспортера с углом наклона 30° поднимают вверх груз массой 40 кг. Какой должна быть сила трения, чтобы груз не скатывался по ленте?
200 Н
ДОМАШНЕЕ ЗАДАНИЕ 32
1.
![]() Два человека одинакового роста держат на плечах за концы
трубу длиной 2 м и массой 10 кг. На расстоянии 0,5 м от первого человека к
трубе подвешен груз массой 100 кг. Определить силы, с которыми труба действует
на плечи первого и второго человека. F1=800H; F2=300H.
Два человека одинакового роста держат на плечах за концы
трубу длиной 2 м и массой 10 кг. На расстоянии 0,5 м от первого человека к
трубе подвешен груз массой 100 кг. Определить силы, с которыми труба действует
на плечи первого и второго человека. F1=800H; F2=300H.
2. Балка длиной 8м и массой 100кг расположена горизонтально и покоится на двух опорах, АМ=3м, МN=3м, NB=2м. На расстоянии 2м от левого конца балки подвешен груз массой 40 кг. Определить реакции опоры. N1=1200H; N2=200H.
3. Однородный стержень массой 0,1кг укреплён одним концом в шарнире и удерживается в равновесии с помощью нити прикреплённой к другому её концу угол α=30о. Найти силу натяжения нити и реакцию опоры шарнира.
Fн=0,29H; N=1,01H.
4. Какую силу надо приложить для равномерного подъема вагонетки массой 600 кг по эстакаде с углом наклона 20°, если коэффициент сопротивления движению равен 0,05?
2,29 кН
Контрольно-измерительные материалы
Самостоятельная работа №1
I ВАРИАНТ
1. Движение точки на плоскости описывается уравнениями х = 6 + 3t, у = 4t. Определить траекторию движения точки и построить ее на плоскости ХОУ.
2. Из городов А и В, расстояние между которыми 120 км, одновременно выехали навстречу две автомашины, скорости которых постоянны и равны 20 км/ч и 60 км/ч. Найти, через какое время и на каком расстоянии от города С, находящегося на полпути между А и В, встретятся автомобили.
1,5ч. 30км.
3. Моторная лодка проходит по реке от пунктаА до пункта В расстояние за 4 часа, а обратно — за 5 часов. Определите скорость течения реки, если расстояние между пунктами 80 км. 2км/ч
4. Тело, имея начальную скорость 5 м/с, прошло за пятую секунду путь, равный 4,5 м. Определить ускорение и путь, пройденный телом за 10 с. -0,11м/с2. 44,5м
5. Мальчик вращает камень, привязанный к веревке длиной 0,5 м в вертикальной плоскости так, что частота равна 3 об/с. На какую высоту взлетел камень, если веревка оборвалась к тот момент, когда скорость была направлена вертикально вверх?
II ВАРИАНТ
1. Точка М совершает движение на плоскости ХОУ. Координаты точки в зависимости от времени изменяются так: х = -4t, у = 6 + 2t. Записать уравнение траектории у = у(х) точки
2. Из двух пунктов, расстояние между которыми 100 м, одновременно навстречу друг другу начали двигаться два тела. Скорость одного из них 20 м/с. Какова скорость второго тела, если они встретились через 4 с? Начало координат поместите в пункте нахождения тела, скорость которого известна.
5м/с.
3. Между двумя пунктами, расположенными на реке на расстоянии 100 км один от другого, курсирует катер, который, идя по течению, проходит это расстояние за время 4 часа, а против течения — за время 10 ч. Определить скорость течения реки и скорость катера относительно воды.
7,5км/ч
4. Пуля, летящая со скоростью 400 м/с, ударяет в земляной вал и проникает в него на глубину 36 см. Сколько времени двигалась она внутри вала? С каким ускорением? Какова была ее скорость на глубине 18 см?
-4 5 2 .
1,8·10 с. 2,21·10 м/с . 282м/с
5. Пропеллер самолета радиусом 1,5 м вращается при посадке с частотой 2000 мин-1, посадочная скорость самолета относительно Земли равна 162 км/ч. Определите скорость точек на конце пропеллера. Какова траектория движения этой точки?
Самостоятельная работа №2
I ВАРИАНТ
1. Движение точки на плоскости описывается уравнениями х = 6 + 3t, у = 4t. Определить траекторию движения точки и построить ее на плоскости ХОУ.
2. Из городов А и В, расстояние между которыми 120 км, одновременно выехали навстречу две автомашины, скорости которых постоянны и равны 20 км/ч и 60 км/ч. Найти, через какое время и на каком расстоянии от города С, находящегося на полпути между А и В, встретятся автомобили.
1,5ч. 30км.
3. Моторная лодка проходит по реке от пунктаА до пункта В расстояние за 4 часа, а обратно — за 5 часов. Определите скорость течения реки, если расстояние между пунктами 80 км.
2км/ч
4. Тело, имея начальную скорость 5 м/с, прошло за пятую секунду путь, равный 4,5 м. Определить ускорение и путь, пройденный телом за 10 с. -0,11м/с2. 44,5м
5. Мальчик вращает камень, привязанный к веревке длиной 0,5 м в вертикальной плоскости так, что частота равна 3 об/с. На какую высоту взлетел камень, если веревка оборвалась к тот момент, когда скорость была направлена вертикально вверх?
II ВАРИАНТ
1. Точка М совершает движение на плоскости ХОУ. Координаты точки в зависимости от времени изменяются так: х = -4t, у = 6 + 2t. Записать уравнение траектории у = у(х) точки
2. Из двух пунктов, расстояние между которыми 100 м, одновременно навстречу друг другу начали двигаться два тела. Скорость одного из них 20 м/с. Какова скорость второго тела, если они встретились через 4 с? Начало координат поместите в пункте нахождения тела, скорость которого известна.
5м/с.
3. Между двумя пунктами, расположенными на реке на расстоянии 100 км один от другого, курсирует катер, который, идя по течению, проходит это расстояние за время 4 часа, а против течения — за время 10 ч. Определить скорость течения реки и скорость катера относительно воды.
7,5км/ч
4. Пуля, летящая со скоростью 400 м/с, ударяет в земляной вал и проникает в него на глубину 36 см. Сколько времени двигалась она внутри вала? С каким ускорением? Какова была ее скорость на глубине 18 см?
-4 5 2. 282м/с.
1,8·10 с. 2,21·10 м/с
5. Пропеллер самолета радиусом 1,5 м вращается при посадке с частотой 2000 мин-1, посадочная скорость самолета относительно Земли равна 162 км/ч. Определите скорость точек на конце пропеллера. Какова траектория движения этой точки?
Самостоятельная работа №3
I ВАРИАНТ
1. Вагон массой 20 т, движущийся со скоростью 0,3 м /с, нагоняет вагон массой 30 т, движущийся со скорость 0,2 м /с, после упругого столкновения второй вагон стал двигаться со скоростью 0,25 м /с. Определить скорость первого вагона?
2. Чему равен ежесекундный расход топлива в момент старта ракеты массой 106 кг, если она стартует вертикально с ускорением 3м/с2. Скорость истечения газов относительно ракеты 4000м/с.
Отв: 3,25•103 кг/с.
3. Определите ускорение свободного падения на Луне, если масса Луны 7,31022 кг. Радиус Луны принять равным 1700 км. 1,6 м/с2
4. В вершинах при основании прямоугольного равнобедренного треугольника расположены одинаковые точечные заряды Q1 = Q2 = 2х10-8 Кл. Расстояние AB между зарядами равно 0,6 м. Определить силу, действующую на заряд Q3 = -3 х10-8 Кл, находящийся в вершине угла C.
5. Радиус планеты Марс составляет 0,53 радиуса Земли, а масса – 0,11 массы Земли. Зная напряжённость гравитационного поля на поверхности Земли найти напряжённость поля на поверхности Марса. 3,8 Н/кг
6. Определить скорость движения спутника на расстоянии 6400 км от поверхности Земли.
II ВАРИАНТ
1. Вагон массой 10 т двигается со скоростью 0,1 м/с. Навстречу ему двигается вагон массой 30т со скоростью 0,5 м/с. Определить скорость вагонов после срабатывания автосцепки.
2. Чему равен ежесекундный расход топлива в момент старта ракеты массой 10т, если она стартует вертикально с ускорением 1м/с2. Скорость истечения газов относительно ракеты 5000м/с.
3. Каково расстояние между покоящимися шарами массой 100 кг каждый, если они притягиваются друг к другу с силой, равной 0,1 Н?
2,58 мм
4. Заряд электрона е = 1, 6x10-19 Кл. Определить скорость движения электрона по орбите атома водорода, если её радиус равен R=5,3x10-11м.
5. Средняя плотность Венеры 5200 кг/м3, а радиус планеты 6100 км. Найти напряжённость гравитационного поля на поверхности Венеры.
6. Определить наибольшую высоту подъёма тела, брошенного со скоростью 30 м/с с поверхности Земли.
Самостоятельная работа №4
1. Электрон влетает в электрическое поле против силовых линий. Напряжённость поля 3•10-8 В/м. Сколько времени потребуется ему для возврата в исходную точку, если начальная скорость электрона 4•106 м/с.
2. С самолета, летящего со скоростью 200 м/с произведен выстрел горизонтально с начальной скоростью 600 м/с. На сколько снаряд отклонился от горизонтали, если до цели 500м?
3. Капелька жидкости находится в равновесии в восходящем потоке воздуха, направленном вертикально вверх. Определить массу капельки, если сила сопротивления воздуха 2•10-4 Н.
4. Положительно заряженная капелька жидкости находится в равновесии в однородном электрическом поле, направленном вертикально вверх напряженностью 196 Н/Кл. Определить заряд капельки, если её масса - 2•10-4 г.
5. Электрон, влетающий в однородное магнитное поле под углом 60о к направлению поля, движется по винтовой линии радиусом 1см с периодом обращения 20мкс. Какова скорость электрона, индукция магнитного поля и шаг винтовой линии?
6. На какой угол от первоначального движения отклонится электрон в магнитном поле толщиной 4,1 см и индукцией 2,1х10-4 Тл, если скорость его 2,4х 105 м/с
1. С балкона на высоте 45м от земли вертикально вверх бросили мяч со скоростью 25м/с. Определить время движения до Земли и скорость во время падения?
2. Положительно заряженная капелька жидкости находится в равновесии в однородном электрическом поле, направленном вертикально вверх напряженностью 300 Н/Кл. Определить заряд капельки, если её масса - 2•10-4 г.
3. В тормозящее электрическое поле толщиной 6см и напряжённостью 100 Н/Кл влетает заряженная частица массой 0,2г и зарядом 1,5·10-4Кл. С какой начальной скоростью должна лететь частица, чтобы преодолеть это поле?
4. Электрон влетает в однородное магнитное поле со скоростью 10000 км/с перпендикулярно его линиям магнитной индукции. Определить модуль магнитной индукции поля, если электрон движется по окружности радиусом 2 см.
5. Электрон, влетающий в однородное магнитное поле под углом 60о к направлению поля, движется по винтовой линии радиусом 5см с периодом обращения 60мкс. Какова скорость электрона, индукция магнитного поля и шаг винтовой линии?
6. С самолета, летящего со скоростью 300 м/с произведен выстрел горизонтально с начальной скоростью 500 м/с. На сколько снаряд отклонился от горизонтали, если до цели
500м?
Самостоятельная работа №5
1. Тело массой 100 кг, двигавшееся вертикально вниз со скоростью 6 м/с, тормозится до остановки в течение 4 с. Считая движение равнозамедленным, определить силу натяжения каната.
1,13 кН
2. Лыжник массой 60 кг, имеющий в конце спуска скорость 10 м/с, останавливается через 40 с после окончания спуска. Определить величину силы сопротивления. 15 Н
3.
![]() Два груза массами т1 = 200 г и m2 = 300 г связаны нитью и
лежат на гладкой горизонтальной поверхности стола. С каким ускорением будут
двигаться грузы, если к грузу т1 приложить силу F = 1,5 Н, направленную
параллельно плоскости стола? Какую силу натяжения будет испытывать при этом
нить, связывающая тела?
Два груза массами т1 = 200 г и m2 = 300 г связаны нитью и
лежат на гладкой горизонтальной поверхности стола. С каким ускорением будут
двигаться грузы, если к грузу т1 приложить силу F = 1,5 Н, направленную
параллельно плоскости стола? Какую силу натяжения будет испытывать при этом
нить, связывающая тела?
3 м/с2 0,9 Н
4. На гладком столе лежат два бруска с массами m1 = 400 г и m2 — 600 г. К одному из них приложена горизонтальная сила F = 2 Н. Определите силу Т натяжения нити, если сила приложена: а) к первому бруску; б) ко второму бруску.
а) 1,2 Н б) 0,8 Н
5. С высоты 25 м предмет падал в течение 2,5 с. Какую часть составляет средняя сила сопротивления воздуха от силы тяжести? 0,2
6. При каком ускорении разорвется трос при подъеме груза массой 500 кг, если максимальная сила натяжения, которую выдерживает трос не разрываясь, равна 15 кН?
2
20 м/с
7. Состав какой массы может везти тепловоз с ускорением 0,1 м/с2 при коэффициенте сопротивления 0,005, если он развивает максимальное тяговое усилие 300 кН?
2000 т
8. По горизонтальной плоскости движется груз массой 10 кг под действием силы 50 Н, направленной под углом 60° к горизонту. Определить, с каким ускорением движется груз. С какой силой он давит на плоскость? Трением между грузом и плоскостью пренебречь.
2,5 м/с2 5,5 Н
9.
![]() Спортсмен массой 65 кг, прыгая с десятиметровой вышки,
входит в воду со скоростью 13 м/с. Найти среднюю силу сопротивления воздуха. 100
Н
Спортсмен массой 65 кг, прыгая с десятиметровой вышки,
входит в воду со скоростью 13 м/с. Найти среднюю силу сопротивления воздуха. 100
Н
10. Два груза массами 1 кг и 2 кг подвешены на нити: второй груз тянут с силой 3 Н. В некоторый момент верхнюю нить пережигают. Определить, с каким ускорением начнут двигаться грузы. Чему равна сила натяжения нити, связывающей грузы 1 и 2?
10,8 м/с2 1 Н
Самостоятельная работа №6
1.
![]() Груз массой m1 находится на наклонной
плоскости, образующей угол α с горизонтом. Коэффициент трения равен
μ. На нити, привязанной к грузу и переброшенной через блок, подвешен груз
массой m2. При какой величине m2система будет находиться
в равновесии?
Груз массой m1 находится на наклонной
плоскости, образующей угол α с горизонтом. Коэффициент трения равен
μ. На нити, привязанной к грузу и переброшенной через блок, подвешен груз
массой m2. При какой величине m2система будет находиться
в равновесии?
m1(sinα-μcosα) <m1(sinα+μcosα), если tgα> μ; 0 <m1(sinα+μcosα), если tgα< μ
2.
![]()
![]()
![]() На шкив радиусом R=20
см намотана нить, к которой подвешен груз. Груз отпускают без начальной
скорости, и он опускается с ускорением 2 м/с2. Какова угловая
скорость ω шкива в тот момент, когда груз прошёл путь S=1м? Найдите также
ускорение точки А в этот момент. ω= 2RSa =1рад/сек, аА
= а 4RS22 1
0,20м/с2.
На шкив радиусом R=20
см намотана нить, к которой подвешен груз. Груз отпускают без начальной
скорости, и он опускается с ускорением 2 м/с2. Какова угловая
скорость ω шкива в тот момент, когда груз прошёл путь S=1м? Найдите также
ускорение точки А в этот момент. ω= 2RSa =1рад/сек, аА
= а 4RS22 1
0,20м/с2.
3.
![]()
![]()
![]() Через блок,
укреплённый на ребре призмы, перекинута нить с грузами на концах. Найдите
ускорение грузов а и силу натяжения нити Т. Трением пренебречь. а m2 sin m2 sin g ; Т
m1m2g(sinsin)
Через блок,
укреплённый на ребре призмы, перекинута нить с грузами на концах. Найдите
ускорение грузов а и силу натяжения нити Т. Трением пренебречь. а m2 sin m2 sin g ; Т
m1m2g(sinsin)
m1 m2 m1 m2
![]()
4. Найдите ускорения а1 и а2 показанных на рисунке грузов и силу натяжения нити Т.
a1 ![]() 2(2m1 m2)
g ; a2
2(2m1 m2)
g ; a2 ![]() 2m1
m2 g ; T
2m1
m2 g ; T
![]() 3m1m2
3m1m2
4m1 m2 4m1 m2 4m1 m2
Самостоятельная работа №7
1.
![]() Определить работу гравитационных сил при перемещении
космического корабля массой 100т из точки С в точку D, если в точке А
находится Земля, а в точке В – Луна. АС = 2•106 м.
Определить работу гравитационных сил при перемещении
космического корабля массой 100т из точки С в точку D, если в точке А
находится Земля, а в точке В – Луна. АС = 2•106 м.
2. Какую скорость может сообщить электрону, находящемуся в состоянии покоя, ускоряющая разность потенциалов электрического поля
250 мкВ? Масса электрона 9,1•10-31 кг.
3. Между двумя плоскими пластинами, к которым приложена разность потенциалов 300В, находится во взвешенном состоянии пылинка массой 2•10-7 г. Расстояние между пластинами 1 см. Определить электрический заряд пылинки.
4. Определить напряжённость гравитационного поля на расстоянии 7000км от центра Земли.
![]()
5. Определить разность потенциалов, пройденную зарядом 3•10-6 Кл, если электростатическое поле совершило работу 15•10-6 Дж.
1. Определить работу гравитационных сил при перемещении космического корабля массой 100т из точки С в точку D. В точке А находится Земля. В точке В находится Луна.
2. Какова разность потенциалов тормозящего электрического поля, если скорость электрона 3•106 м/с упала до нуля?
3. Между двумя плоскими пластинами, к которым приложена разность потенциалов 150В, движется равномерно вверх пылинка массой 3•10-7 г. Расстояние между пластинами 6 см. Определить электрический заряд пылинки.
4. Определить напряжённость гравитационного поля на расстоянии 5000км от центра Луны.
5. Определить работу электростатических сил по перемещению заряда 1,5•10-6 Кл из точки с потенциалом 1В в точку с потенциалом 5В
Самостоятельная работа №8
![]() 1. Незаряженный конденсатор
ёмкостью 100 мкФ соединили параллельно с конденсатором ёмкостью 50 мкФ,
заряженным до напряжения 300 В. Какое напряжение установилось на конденсаторах?
Как распределился заряд между ними?
1. Незаряженный конденсатор
ёмкостью 100 мкФ соединили параллельно с конденсатором ёмкостью 50 мкФ,
заряженным до напряжения 300 В. Какое напряжение установилось на конденсаторах?
Как распределился заряд между ними?
100 В; 10-2 Кл; 0,5·10-2 Кл
2. Определить электроёмкость батареи конденсаторов, если C1 = С2 = 2 нФ и С3 = 500 пФ.
444,4 пФ
3. Определить электрическую ёмкость батареи конденсаторов, если конденсаторы имеют одинаковую ёмкость, равную 0,6 мкФ.
0,24 мкФ
4. Определить электроёмкость представленной на рисунке батареи одинаковых конденсаторов. Сб=2С
![]()
1. Два одинаково плоских конденсатора соединены параллельно и заряжены до разности потенциалов 150 В. Определить разность потенциалов на конденсаторах, если после отключения их от источника тока у одного конденсатора уменьшили расстояние между пластинами в два раза.
100 В
2.
![]() Определить электроёмкость батареи конденсаторов, если С1 =
0,1 мкФ, С2 = 0,4 мкФ и С3 = 0,52 мкФ.
Определить электроёмкость батареи конденсаторов, если С1 =
0,1 мкФ, С2 = 0,4 мкФ и С3 = 0,52 мкФ.
0,6 мкФ
3. Определить электроёмкость батареи конденсаторов, если C1 = 2 мкФ, С2 = 4 мкФ и С3 = 1 мкФ. С4 = 2 мкФ, С5 = 6 мкФ.
1,5 мкФ
4. Определить электроёмкость представленной на рисунке батареи одинаковых конденсаторов. Сб=6С
Самостоятельная работа №9
1. Автомобиль массой 2 т трогается с места с ускорением 2 м/с2 и разгоняется в течение 5 с на горизонтальном пути. Какая работа совершается за это время, если коэффициент сопротивления 0,01? 1,1 105 Дж
2. Какую работу совершит сила F = 30 Н, подняв по наклонной плоскости груз массой 2 кг на выступ 2,5 м с ускорением 10 м/с2. Сила действует параллельно наклонной плоскости. Трением о плоскость пренебречь.
147 Дж
3. Груз массой 25 кг висит на шнуре длиной 2,5 м. На какую наибольшую высоту можно отвести в сторону груз, чтобы при дальнейших свободных качаниях шнур не оборвался? Максимальная сила натяжения, которую выдерживает шнур не обрываясь, равна 550 Н.
1,6 м
4. С какой максимальной скоростью может ехать по горизонтальной плоскости мотоциклист, описывая дугу радиусом 90 м, если коэффициент трения резины о почву 0,4? На какой угол от вертикали он при этом отклонится? 18,8 м/с 22о
5. Конькобежец проезжает по гладкой поверхности льда по инерции 80 м. Определите величину работы по преодолению трения, если масса конькобежца 60 кг, а коэффициент трения 0,015.
720 Дж
1. Лифт массой 1000 кг равноускорено поднимался лебедкой. На некотором отрезке пути длиной 1 м лифт двигался со средней скоростью 5 м/с и его скорость возросла на 0,5 м/с. Какую работу совершила сила, перемещающая лифт на указанном отрезке его пути?
12,8 кДж
2.
![]() Велосипедист должен проехать по «чертовому колесу», радиус
которого 8 м. С какой высоты велосипедист может начать движение, чтобы не
упасть? Трение не учитывать.
Велосипедист должен проехать по «чертовому колесу», радиус
которого 8 м. С какой высоты велосипедист может начать движение, чтобы не
упасть? Трение не учитывать.
20 м
3. Пуля массой 10 г, летевшая горизонтально со скоростью 600 м/с, ударилась в свободно подвешенный деревянный брусок массой 5 кг и застряла в нем, углубившись на 10 см. Найти силу сопротивления движению пули.
18 кН
4. Маятник массой 5 кг отклонен на угол 60° от вертикали. Какова сила натяжения нити при прохождении маятником положения равновесия? 98 Н
5. Конькобежец движется со скоростью 10 м/с по окружности радиусом 40 м. Под каким углом к горизонту он должен наклонится, чтобы не упасть?
76o
Самостоятельная работа №10
1. Мяч был брошен под углом к горизонту равным 30° с начальной скоростью 20 м/с. Найти дальность полета.
35 м
2. Из шланга, лежащего на земле, бьет под углом 45° к горизонту вода с начальной скоростью 10 м/с. Площадь сечения отверстия шланга 5 см2. Определите массу т струи, находящейся в воздухе. 7,2 кг
3. Локомотив развивает постоянную силу тяги 3,5105 Н. На горизонтальном участке пути 600 м скорость поезда возросла с 10 м/с до 20 м/с. Определить коэффициент трения, если масса поезда 106 кг. 0,01
4. Лифт опускается равноускоренно и в первый 10 с проходит путь 10 м. На сколько уменьшится вес пассажира массой 70 кг, который находится в этом лифте? 14 Н
5. Пружина жесткостью 100 Н/м под действием силы удлинилась на 5 см. Какова жесткость другой пружины, которая под действием такой же силы удлинилась на 1 см?
500 Н/м
1. Найти максимальную высоту подъема камня, брошенного с начальной скоростью 10 м/с под углом в 45° к горизонту.
2,5 м
2. Камень, брошенный под углом к горизонту, упал на землю через 4 с. Чему равны высота и дальность полета камня, если известно, что во время движения его максимальная скорость была вдвое больше минимальной.
20 м 45 м
3. Мальчик массой 50 кг, скатившись на санках с горки, проехал по горизонтальной дороге до остановки путь 20 м за 10 с. Найти силу трения и коэффициент трения.
20 Н 0,04
4. Чему будет равен вес груза массой 100 кг при равноускоренном подъеме его в лифте, если известно, что лифт достиг скорости 3 м/с, пройдя путь 18 м? 1 кН
5. На сколько удлинится рыболовная леска жесткостью 0,5 Н/м при поднятии вертикально вверх рыбы массой 200 г?
4 мм
Календарно-тематическое планирование
|
|
|
Название темы/урока |
|
|
|
Введение. (3 часа). |
|
1. |
1. |
Материя. Свойства материи. Физические величины. |
|
2. |
2. |
Погрешности |
|
3. |
3. |
Решение задач по теме "Погрешности". |
|
|
|
Основные понятия кинематики (20 часов). |
|
4. |
1. |
Основная задача механики. Материальная точка. Система отсчёта. Радиус-вектор. Траектория. Путь. Перемещение. |
|
5. |
2. |
Равномерное прямолинейное движение. Скорость Перемещение. Уравнение движения. |
|
6. |
3. |
Графическое представление движения. |
|
7. |
4. |
Решение задач по теме "Графическое представление движения" |
|
8. |
5. |
Относительность движения. |
|
9. |
6. |
Решение задач |
|
10. |
7. |
Средняя скорость. |
|
11. |
8. |
Мгновенная скорость. Ускорение. Равноускоренное движение. Уравнение движения. |
|
12. |
9. |
Решение задач по теме "Уравнение движения" |
|
13. |
10. |
Графическое представление движения |
|
14. |
11. |
Решение задач по теме «Графики РУД» |
|
15. |
12. |
Л/р №1 "Исследование зависимости скорости от времени" |
|
16. |
13. |
Л/Р №2 "Исследование зависимости перемещения от времени" |
|
17. |
14. |
Кинематика периодического движения. Движение по окружности |
|
18. |
15. |
Характеристики вращательного движения |
|
19. |
16. |
Решение задач по теме "Движение по окружности" |
|
20. |
17. |
Решение задач по теме "Кинематика" |
|
21. |
18. |
Расчёт передач |
|
22. |
19. |
Решение задач по теме «Движение по окружности» |
|
23. |
20. |
Контрольная работа №1 по теме «Кинематика материальной точки. |
|
|
|
Взаимодействие тел. Законы механики Ньютона. (10 часов). |
|
24. |
1. |
Сила. III закон Ньютона. Закон Гука. Измерение силы. II закон Ньютона. |
|
25. |
2. |
Закон сохранения импульса. II закон Ньютона. |
|
26. |
3. |
Решение задач по теме "II закон Ньютона". |
|
27. |
4. |
Решение задач по теме "Закон сохранения Импульса" |
|
28. |
5. |
Реактивное движение. Уравнение Мещерского. Формула Циолковского. |
|
29. |
6. |
Решение задач по теме "Закон сохранения импульса". |
|
30. |
7. |
Решение задач. Самостоятельная работа. |
|
31. |
8. |
Энергия. Механическая работа. Теорема о кинетической энергии. |
|
32. |
9. |
Решение задач по теме "Работа. Мощность. Энергия. |
|
33. |
10. |
Решение задач |
|
|
|
Поля. Характеристики полей. Фундаментальные взаимодействия. (18 час) |
|
34. |
1. |
Векторные поля. Поток вектора. Циркуляция вектора. |
|
35. |
2. |
Гравитационное взаимодействие. Закон всемирного тяготения. |
|
36. |
3. |
Решение задач по теме "Гравитационное взаимодействие". |
|
37. |
4. |
Вес тела. Решение задач. |
|
38. |
5. |
Самостоятельная работа по теме "Гравитационное взаимодействие и вес". |
|
39. |
6. |
Электрическое взаимодействие. Закон Кулона. |
|
40. |
7. |
Решение задач по теме "Электростатика" |
|
41. |
8. |
Решение задач по теме "Электростатика" |
|
42. |
9. |
Самостоятельная работа по теме "Электростатика". |
|
43. |
10. |
Магнитное поле. Характеристики магнитного поля. |
|
44. |
11. |
Решение задач по теме "Сила Лоренца" |
|
45. |
12. |
Движение в однородных полях. |
|
46. |
13. |
Решение задач по теме "Скорость со направлена с силой" |
|
47. |
14. |
Начальная скорость перпендикулярна силе. |
|
48. |
15. |
Л/р №4 "Изучение движения тела, брошенного горизонтально" |
|
49. |
16. |
Начальная скорость направлена под углом к силе. |
|
50. |
17. |
Решение задач |
|
51. |
18. |
Самостоятельная работа |
|
|
Силы в природе (23 час) |
|
|
52. |
1. |
Сила трения |
|
53. |
2. |
Сила сопротивления среды |
|
54. |
3. |
Трение в жидкостях и газах. |
|
55. |
4. |
Решение задач по теме «Сила трения» |
|
56. |
5. |
Л/р №5 "Определение коэффициента трения" |
|
57. |
6. |
Движение под действием нескольких сил |
|
58. |
7. |
Решение задач по теме "Движение на поворотах" |
|
59. |
8. |
Наклонная плоскость |
|
60. |
9. |
Неподвижный блок. |
|
61. |
10. |
Решение задач по теме "Неподвижный блок" |
|
62. |
11. |
Решение задач по теме "Наклонная плоскость" |
|
63. |
12. |
Самостоятельная работа |
|
64. |
13. |
Подготовка к контрольной работе |
|
65. |
14. |
Контрольная работа №2 |
|
66. |
15. |
Работа силы тяжести. Закон сохранения энергии. |
|
67. |
16. |
Работа силы упругости. |
|
68. |
17. |
Закон сохранения энергии. |
|
69. |
18. |
Решение задач по теме «Закон сохранения энергии» |
|
70. |
19. |
Коэффициент полезного действия. |
|
71. |
20. |
Л/р Определение КПД |
|
72. |
21. |
Самостоятельная работа по теме «Закон сохранения энергии» |
|
73. |
22. |
Подготовка к контрольной работе |
|
74. |
23. |
Контрольная работа №3 |
|
|
|
Энергетическая характеристика полей (5 час) |
|
75. |
1. |
Потенциал. Разность потенциалов. |
|
76. |
2. |
Решение задач по теме «Потенциал» |
|
77. |
3. |
Ёмкость. Теплоёмкость. Электроёмкость. |
|
78. |
4. |
Решение задач по теме "Ёмкость". |
|
79. |
5. |
Решение задач по теме «Ёмкость» |
|
|
Колебательное движение (11 час) |
|
|
80. |
1. |
Координаты тела, движущегося по окружности. |
|
81. |
2. |
Колебательное движение. Вынужденные колебания. Квазиупругая сила |
|
82. |
3. |
Свободные колебания. Движение под действием силы упругости. |
|
83. |
4. |
Сложение колебаний. |
|
84. |
5. |
Энергия тела, совершающего колебания. |
|
85. |
6. |
Математический маятник. |
|
86. |
7. |
Решение задач по теме "Колебания" |
|
87. |
8. |
Самостоятельная работа |
|
88. |
9. |
Автоколебания. |
|
89. |
10. |
Резонанс |
|
90. |
11. |
Контрольная работа по теме "Колебания" |
|
|
|
Условия равновесия твёрдого тела (6 час) |
|
91. |
1. |
Условия равновесия тела, на плоскости. |
|
92. |
2. |
Условие равновесия тела , имеющего ось вращения. Момент силы. Лабораторная работа |
|
93. |
3. |
Решение задач по теме "Условия равновесия". |
|
94. |
4. |
Момент импульса. Момент инерции. Основной закон динамики вращательного движения. |
|
95. |
5. |
Закон сохранения момента импульса. |
|
96. |
6. |
Решение задач |
Название этой книги отражает стремление дать учебник, пригодный для ознакомления с элементами физики как науки. Это – задача, которую должно ставить себе преподавание в старших классах общеобразовательной организации и профессиональной образовательной организации. Поэтому принципиальные установки, положенные в основу книги справедливы для таких организаций любой направленности.
Установки эти сообщают книге некоторые особенности, отличающие её от существующих учебников.
У педагогических работников образовательной организации высшего образования сложилось мнение, что знания по физике, с которыми приходят обучающиеся из общеобразовательной организации, стоят на совершенно неудовлетворительном уровне. Обучаемые зачастую плохо ориентируются в том, что положено в основу как определение, что является результатом опыта, на что следует смотреть как на теоретическое обобщение этих опытов. Нередко новые факты расцениваются как самоочевидные следствия, и поэтому всё глубокое значение этих фактов остаётся неосознанным, или, наоборот, различные формулировки одних и тех же положений воспринимаются как разные закономерности.
Конечно, по объёму учебного материала, по глубине изложения, по использованию сложного математического материала преподавание в образовательной организации высшего образования существенно отличается от преподавания на более ранних ступенях. Однако и на этих ступенях преподавать физику нужно именно как науку, а не совокупность отдельных фактов. Необходимо, чтобы обучающиеся осознали, что определения, формулируемые логически, наполняются содержанием лишь при помощи опыта, через посредство измерений.
Не менее важную роль в обучении играет правильное представление о структруировании целого комплекса явлений, для того чтобы видеть картину в целом, а не только отдельные её аспекты. Необходимо научить обучающегося видеть в разных, казалось бы процессах общие закономерности.
Важным вопросом становится моделирование процесса. Смысл моделирования состоит в том, чтобы пренебречь чертами явления, несущественными для рассматриваемого комплекса вопросов, но сохранить то, что необходимо. В этом смысле моделирование явления может происходить по-разному в зависимости от изучаемой стороны дела. Одними из распространённых моделей являются представления об абсолютно твёрдом теле, несжимаемой жидкости, идеальном газе.
Преподавание в общеобразовательной организации должно строиться таким образом, чтобы в дальнейшем обучающийся мог и должен был доучиваться.
Большое значение имеет расчленение сложного явления на более простые, облегчающие изучение явления по частям. Наблюдения над сложными явлениями показывают, что при таком расчленении можно выделить группу сходных явлений, например, оптические, тепловые, электрические и т. д, поэтому целесообразно и при изучении физики объединить исследуемый материал в такие группы. Распределение учебного материала по группам (а также их последовательность)не является чем-то строго обязательным и может быть проведено различным образом. Что я и сделал.
Бибиков Д.Н.
Список литературы:
1. Яворский Б.М. Пинский А.А. «Основы Физики». Наука. М. 1974
2. Корчагин Е.В. Физика М. 2001
3. Лансберг Г.С. Элементарный учебник физики. Наука. М.1968.
4. Бутиков Е.И. Физика в примерах и задачах. Наука. М. 1989.
5. Яворский Б.М. Детлаф А.А. Справочник по физике. М. 1963.
6. Вереина Л.И. Техническая механика. М. 2007
7. Бессонов Л.А. Теоретические основы электротехники. М. 1964.
8. Буховцев Б.Б. Сборник задач по элементарной физике. М. «Наука» 1987.
9. Поляков В.Т. Посвящение в радиоэлектронику. М. «Радиосвязь» 1988.
10. Гладкова Р.А. Сборник задач и вопросов по физике. М. «Наука» 1988.
11. Фетисов Г.П. Материаловедение и технология металлов. М. ОНИКС. 2009.
ОГЛАВЛЕНИЕ
1. ПОНЯТИЕ О МАТЕРИИ 2
2. ПОГРЕШНОСТИ 5
3. ОСНОВНАЯ ЗАДАЧА МЕХАНИКИ. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ 10
4. РАВНОМЕРНОЕ ДВИЖЕНИЕ 14
5. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ 14
6. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ 17
7. НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ. СРЕДНЯЯ СКОРОСТЬ . 20 8. РАВНОПЕРЕМЕННОЕ ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ. УСКОРЕНИЕ. 23 9. ПЕРЕМЕЩЕНИЕ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОПЕРЕМЕННОМ ДВИЖЕНИИ 25
10. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ 32
11. ПЕРИОД И ЧАСТОТА. УГЛОВАЯ СКОРОСТЬ. 36
12. РАСЧЁТ ПЕРЕДАЧ. 38
13. КООРДИНАТЫ ТЕЛА, ДВИЖУЩЕГОСЯ ПО ОКРУЖНОСТИ 41
14. СИЛА 43
15. ИМПУЛЬС. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА. 46
16. РЕАКТИВНОЕ ДВИЖЕНИЕ 49
17. ЭНЕРГИЯ. МЕХАНИЧЕСКАЯ РАБОТА 51 18. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ 53
19. ВЕКТОРНЫЕ ПОЛЯ 55
20. ЛАМИНАРНОЕ ТЕЧЕНИЕ ЖИДКОСТИ 56 21. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ ЖИДКОСТИ 57
22. ГРАВИТАЦИОННОЕ ПОЛЕ 59
23. СТРОЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ 62
24. ВЕС ТЕЛА 66
25. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 69
26. МАГНИТНОЕ ПОЛЕ 75
27. ДВИЖЕНИЕ ТЕЛА В ОДНОРОДНЫХ ПОЛЯХ 80
28. СИЛЫ ТРЕНИЯ 87
29. ДВИЖЕНИЕ ТЕЛ ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ 91
30. РАБОТА СИЛЫ ТЯЖЕСТИ 94
31. РАБОТА СИЛЫ УПРУГОСТИ 96
32. КОЭФФИЦИЕНТ ПОЛЕЗНОГОДЕЙСТВИЯ 98
33. ПОТЕНЦИАЛ. РАБОТА И РАЗНОСТЬ ПОТЕНЦИАЛОВ. 102 34. ЁМКОСТЬ. ТЕПЛОЁМКОСТЬ. ЭЛЕКТРОЁМКОСТЬ. КОНДЕНСАТОРЫ. 109
35. СОЕДИНЕНИЕ КОНДЕНСАТОРОВ 111
36. УРАВНЕНИЕ ДВИЖЕНИЯ ТОЧКИ, РАВНОМЕРНО ДВИИЖУЩЕЙСЯ ПО
113
ОКРУЖНОСТИ. КОЛЕБАНИЯ.
37. ВЫНУЖДЕННЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ. 115
38. СЛОЖЕНИЕ КОЛЕБАНИЙ 116
39. СВОБОДНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ 117
40. УСЛОВИЯ РАВНОВЕСИЯ ТВЁРДОГО ТЕЛА. ВИДЫ РАВНОВЕСИЯ. МОМЕНТ
120
СИЛЫ
41. КОНТРОЛЬНО -ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ 124
Учебное издание
Бибиков Дмитрий Николаевич
Тела. Поля.
Кинематика и Динамика материальной точки.
Учебное пособие
Издается в авторской редакции
ПОДПИСАНО В ПЕЧАТЬ 12.02.13
УСЛ. ПЕЧ. Л. 7,4. ФОРМАТ 60X84 1/16 ТИРАЖ 80 ЭКЗ. ЗАКАЗ № 113
![]()
«МАОУ ЛИЦЕЙ 180»
603135, Г. Н.НОВГОРОД, ПРОСП. ЛЕНИНА 45/5
ОТПЕЧАТАНО В ИЗДАТЕЛЬСТВЕ «МАОУ ЛИЦЕЙ 180»
603135, Г. Н.НОВГОРОД, ПРОСП. ЛЕНИНА 45/5
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.