Поделиться
Семакин информатика 1.pdf
И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова инооргптип
УГЛУБЛЕННЫЙ УРОВЕНЬ
Учебник для 10 класса
в 2-х частях
Часть 1
Рекомендовано
Министерством образования и науки Российской Федерации к использованию в образовательном процессе в имеющих государственную аккредитацию и реализующих образовательные программы общего образования образовательных учреждениях
Москва
БИНОМ. Лаборатория знаний
2014
удк 004.9
ББК 32.97 сзо
Семакин И. Г.
СЗО Информатика. Углубленный уровень учебник для 10 класса : в 2 ч. Ч. 1 / И. Г. Семакин, Т. Ю. Шеина, Л. В. Шестакова. — М. : БИНОМ. Лаборатория знаний, 2014. — 184 с. : ил.
ISBN 978-5-9963-1811-7 (Ч. 1)
ISBN 978-5-9963-1797-4
Учебник предназначен для изучения курса информатики на углубленном уровне в 10 классах общеобразовательных учреждений. Содержание учебника опирается на изученный в 7—9 классах курс информатики для основной школы и разработано в соответствии с Федеральным государственным образовательным стандартом для среднего (полного) образования 2012 г. Рассматриваются теоретические основы информатики, аппаратное и программное обеспечение компьютера, современные информационные и коммуникационные технологии.
Учебник входит в учебно-методический
комплект, включающий также учебник для 11 класса, практикум и мето
дическое пособие.
удк 004.9 ББК 32.97
Учебное изДание
Семакин Игорь Геннадьевич
Шеина Татьяна Юрьевна
Шестакова Лидия Валентиновна
ИНФОРМАТИКА.
УГЛУБЛЕННЫЙ УРОВЕНЬ
Учебник для 10 класса
В двух частях
Часть первая
Ведущий редактор О. А. Полежаева
Ведущие методисты: И. Л. Сретенская, И. Ю. Хлобыстова
Художники: Н. А. Новак, Я. В. Соловцова, Ю. С. Белаш
Технический редактор Е. В. Денюкова Корректор Е. Н. Клитина
Компьютерная верстка: В. А. Носенко Подписано в печать 18.03.14. Формат 70х 100/16. Усл. печ. л. 14,95. Тираж 15 ООО экз. Заказ 5632.
Издательство «БИНОМ. Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. З
Телефон: (499) 157-5272 e-mail: binom@Lbz.ru http://www.Lbz.ru, http://e-umk.Lbz.ru, http://metodist.Lbz.ru
Отпечатано в ОАО Можайский полиграфшеский комбинат
143200, г. Можайск, ул. Мира, 93. www.oaompk.ru, www.0A()M[1k.p(*) тел.: (495) 745-84-28, (49638) 20-685
ISBN 978-5-9963-1811-7 (Ч. 1)
ISBN 978-5-9963-1797-4 БИНОМ. Лаборатория знаний, 2014
ОТ АВТОРОВ
Уважаемые
старшеклассники!
Этот учебник предназначен для изучения курса «Информатика» в 10 классе на углубленном уровне. Вы уже не новички в информатике. В 7—9 классах вы изучали курс информатики для основной школы. В результате вы получили необходимые базовые знания и умения в этом предмете. В курсе для 7—9 классов вы познакомились с элементами всех основных разделов современной информатики: теоретической информатики, информационных и коммуникационных технологий, социальной информатики.
 |
|||
 |
|||
это второй уровень погружения. Тем из вас,
кто после окончания школы поступит в вузы на профильные по отношению к
информатике специальности, предстоит третий уровень погружения в этот предмет.
Это уже будет профессиональный уровень, в результате освоения которого вы
станете специалистами в какой-то определенной области информатики и
информационно-коммуникационных технологий (ИКТ).
К области информатики относится большое
количество современных профессий, в число которых входят:
математик-программист;
математик,
системный программист; 
специалист по информационным системам; 
специалист
по прикладной информатике в различных областях (экономике, социологии, физике,
экологии и пр.); 
специалист по защите информации; 
инженер
по информационным технологиям в различных областях; 
инженер по
вычислительным машинам, комплексам, системам и сетям; 
инженер по
программному обеспечению вычислительной техники и автоматизированных систем и
ряд других профессий.
Курс информатики углубленного уровня приближает выпускника школы к освоению любой из этих профессий при дальнейшем обучении в системе высшего профессионального образования. В старших классах школы может происходить углубление в отдельные направления информатики путем изучения элективных курсов.
Перечислим наиболее важные качества, которыми должен обладать профессионал в области информатики.
Высокий
уровень математической грамотности. Математической насыщенностью отличаются
такие разделы информатики, как теория кодирования, компьютерная графика,
компьютерное моделирование, криптография, искусственный интеллект и др. Широкое
применение в различных разделах информатики находит математическая логика.
 |
|||
 |
|||
программированием на определенных языках
в определенных системах программирования является обязательным профессиональным
качеством большинства специалистов. Здесь есть большое разнообразие вариантов: системное
программирование, итеЬ-программирование, офисное программирование, сетевое
программирование, программирование интегральных схем и пр. 
Развитое
системное мышление. Работа с большими объемами данных требует умения
систематизировать эти данные для того, чтобы наилучшим образом организовать их
хранение и обработку. Навыки систематизации необходимы специалисту в области
компьютерного моделирования, поскольку построение 
модели начинается с
системного анализа объекта моделирования.
Высокий
уровень самообучаемости, навыки самостоятельного освоения новых средств
информационных технологий. Информационно-коммуникационные технологии быстро
развиваются, поэтому требуют от профессионала непрерывного обновления своих
знаний и умений.
Умение искать,
отбирать и критически оценивать информацик) из различных источников.
Умение
организовывать свою Деятельность, участвуя в коллективной разработке проектов,
эффективно взаимодействуя с коллегами (в том числе в Дистанционной форме).
СоблюДение
правовых и этических норм Деятельности в информационной области.
Ориентация на
современном рынке аппаратных и программНЫХ средств ИКТ.
|
От авторов |
|
Предлагаемый вам курс информатики углубленного уровня содержит всё необходимое для развития перечисленных умений, конечно, при условии ответственного отношения к его изучению.
Заголовки некоторых параграфов помечены значками О Это означает, что материал данного параграфа дополнительный. Он может помочь вам в подготовке проектного задания, реферата, доклада.
К каждому параграфу предлагаются вопросы и задания. Часть из них поможет вам подготовиться к итоговой аттестации.
 |
Авторы курса желают вам успеха в освоении непростого, но очень интересного и актуального учебного предмета!
Навигационные значки
Обратите внимание на символы
навигационной полосы, имеющейся в учебниках. Они означают следующее:
важное
утверждение или определение; вопросы и задания;
О материал для подготовки к итоговой аттестации;
 |
О дополнительный материал; а практические работы на компьютере;
интернет-ресурсы; проектные или исследовательские задания; практикум»
1) Семакин И. Г., Хеннер Е. К., Шеина Т. Ю., Шестакова Л. В. Информатика. Углубленный уровень: практикум для 10—11 классов. — М.: БИНОМ. Лаборатория знаний, 2013.
Глава 1
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ИНФОРМАТИКИ
Информатика это наука об
информации и информационных процессах, протекающих в системах различной природы
(естественных, технических, социальных), а также о способах их автоматизации с
использованием компьютерной техники.
 |
Прикладная ветвь информатики
формируется с появлением электронных вычислительных машин. Таким образом, с
начала своего зарождения информатика объединяет в себе науку об ин
формации —
теоретическую информатику и информационную технику и технологии — прикладную
информатику. По отношению к последней сравнительно недавно в употребление вошел
термин «информационно-коммуникационные технологии» , сокращенно икт.
Понятие информации является центральным понятием информатики. Несмотря на кажущуюся интуитивную ясность термина «информация», для него нет в науке единственно верного опре-
деления .
В бытовом смысле под информацией мы понимаем содержание сообщений, которые человек получает из окружающего мира: общаясь с другими людьми, из книг, из средств массовой информации, из других источников. Принятая информация пополняет наши знания. Словосочетание «владеть информацией» означает что-то знать по интересующему нас предмету. Но даже в таком бытовом смысле слово «информация» стало широко употребляться только с середины ХХ века.
|
|
Теоретические основы информатики |
 |
Рис. 1.1. Технические системы связи
Основатель кибернетики Норберт Винер
анализировал разнообразные процессы управления в живых организмах и в
технических системах. Процессы управления рассматриваются в кибернетике как
информационные процессы. Циркулирование информации в системах управления
обеспечивается посреДством сигналов, передаваемых по информационным каналам
мелсДу управляющими объектами и объектами управления.
Кибернетическая модель управления Винера нашла применение во многих научных областях, в том числе в биологии и медицине. Механизмы нервной деятельности животного и человека изучает нейрофизиология. В этой науке используется следующая модель информационных процессов, происходящих в организме. Поступающая извне информация посредством сигналов электрохимической природы передается от органов чувств по нервным волокнам к нейронам (нервным клеткам) мозга (рис. 1.2). От мозга сигналы той же природы передаются к мышечным тканям. Таким образом осуществляется управление органами движения.
В другой биологической науке генетике используется понятие наследственной информации, заложенной в структуре
|
Информатика и информация |
|
Рис. 1.2. Нейроны мозга
 |
Рис. 1.3. Молекула ДНК
Важнейшим научным и техническим достижением ХХ века
стало создание ЭВМ (компьютера). Компьютер — универсальный программно
управляемый автомат для работы с информацией. Компьютер помогает человеку
хранить большие объемы информации, быстро выполнять ее обработку, принимать
информацию и передавать ее на большие расстояния. В компьютере информация
хранится и обрабатывается в виде двоичных кодов. Понятие информации связывают
со смыслом, с содержанием двоичных 
кодов, а понимать смысл может только
человек. Компьютер же формально хранит, передает, принимает и обрабатывает коды
по программе, составленной человеком. Поэтому корректнее называть двоичные
коды, с которыми работает компьютер, не информацией, а Данными. В информацию
эти данные преобразуются лишь в человеческом сознании.
Философские концепции информации
Понятие информации относится к числу фундаментальных, т. е. является основополагающим для науки и не объясняется через другие понятия. В этом смысле информация встает в один ряд с такими фундаментальными научными понятиями, как вещество, энергия, пространство, время. Осмыслением понятия информации как фундаментального понятия занимается наука философия.
Согласно одной из философских концепций, информация является свойством всего сущего, всех материальных объектов мира. Такая концепция информации называется атрибутивной: информация — атрибут материи во всех ее формах и видах. Информация в мире возникла вместе со Вселенной.
|
|
Теоретические основы информатики |
 |
Третья философская концепция информации антропоцентрическая, согласно которой информация существует лишь в человеческом сознании, в человеческом восприятии. Информационная деятельность присуща только человеку, происходит в социальных системах.
О Система основных понятий
Информатика и информация
Информатика — это наука об информации ц информационных процессах, протекающих в системах различной прироДы, а также о способах их автоматиза иц с использованием компьюте ной техники Понятие инфермациив азличных на х Философия Атрибутивная концепция:
ин о ма ия — всеобщее свойство ат иб мате ии Функциональная концепция:
информация и информационные процессы присущи только живой п и о е являются ее кцией Антропоцентрическая концепция:
информация и информационные процессы присущи только человек
|
Теория информации |
Возникла в процессе развития теории связи (К. Шеннон) |
Информация передается посредством последовательностей сигналов |
|
Кибернетика |
Исследует информационные процессы в системах управления (Н. Винер) |
Информация передается посредством сигналов по каналам связи в системах управления |
|
Вычислительная техника |
Разработка компьютеров программно управляемых автоматических устройств для работы с информацией |
Информация — содержание, закодированное данными (двоичными кодами) в памяти компьютера |
|
Нейрофизиология |
Изучает информационные процессы в механизмах нервной деятельности животного и человека |
Информация передается посредством сигналов электрохимической природы по системе нервных связей организма |
|
Генетика |
Изучает механизмы наследственности, пользуется понятием «наследственная информация» |
Информация закодирована генетическим кодом структурой молекул ДНК, входящих в состав клетки живого организма |
Вопросы и задания
1. Какие существуют основные философские концепции информации?
2. Какая концепция, с вашей точки зрения, является наиболее верной?
З. Благодаря развитию каких наук понятие информации стало широко употребляемым?
|
Информатика и информация |
|
 |
4, В каких
биологических науках активно используется понятие информации? Подготовьте
сообщение с использованием ресурсов Интернета.
5. Что такое наследственная информация?
б. К какой философской концепции, на ваш взгляд, ближе употребление понятия информации в генетике?
7. Если под информацией понимать лишь только то, что распространяется через книги, рукописи, произведения искусства, СМИ, то к какой философской концепции можно будет отнести информацию?
8. Что мы понимаем под информацией в бытовом смысле?
9. Может ли быть такое, что компьютерные данные не несут в себе информацию? Если да, то опишите такую ситуацию.
Информационная деятельность людей связана с реализацией информационных процессов: с хранением, передачей и обработкой информации. При этом важно уметь измерять количество информации. Для измерения чего-либо должна быть определена единица измерения. Например, единицей измерения массы служит килограмм, единицей измерения времени секунда, единицей измерения расстояния — метр. Из курса физики вы знаете, что существуют эталоны для этих единиц.
Как измерить информацию? Это сделать сложнее, так как нет ее универсального определения. Существуют два подхода к измерению информации. Первый подход отталкивается от практических нужд хранения и передачи информации в технических системах и не связан со смыслом (содержанием) информации. Второй же подход рассматривает восприятие информации человеком и поэтому имеет дело со смыслом информации. Рассмотрим подробнее суть этих подходов.
|
|
Теоретические основы информатики |
 |
Алфавитный подход к измерению информации применяется в цифровых (компьютерных) системах хранения и передачи информации. В этих системах используется двоичный способ кодирования информации. Алфавитный подход еще называют объемным подходом. При алфавитном подходе для определения количества информации имеет значение лишь размер (объем) хранимого и передаваемого кода. Из курса информатики 7—9 классов вы знаете, что если с помощью Ёразрядного двоичного кода можно закодировать алфавит, состоящий из символов (где лт — целая степень двойки), то эти величины связаны между собой по формуле:
Число лт называется мощностью алфавита.
Если, например, i = 2, то можно построить 4 двухразрядные комбинации из нулей и единиц, т. е. закодировать 4 символа. При i = З существует 8 трехразрядных комбинаций нулей и единиц (кодируется 8 символов):
|
|
оо |
01 |
10 |
11 |
|
|
|
|
|
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
Английский алфавит содержит 26 букв. Для записи текста нужны еще как минимум шесть символов: пробел, точка, запятая, вопросительный знак, восклицательный знак, тире. В сумме получается расширенный алфавит мощностью 32 символа.
Поскольку 32 = 2 5 , все символы можно закодировать всевоз-
Именно пятиразрядный код использовался в телеграфных аппаратах, появившихся еще в XIX веке. Телеграфный аппарат при вводе переводил английский текст в двоичный код, длина которого в 5 раз больше, чем длина исходного текста.
В двоичном коде каждая двоичная цифра несет одну единицу информации, которая называется 1 бит.
Бит является основной единицей измерения информации.
|
Измерение информации |
|
 |
Информационный объем текста склаДывается из информационных весов всех составляющих текст символов. Например, английский текст из 1000 символов в телеграфном сообщении будет иметь информационный объем 5000 битов.
Алфавит русского языка включает 33 буквы. Если к нему добавить еще пробел и пять знаков препинания, то получится набор из 39 символов. Для двоичного кодирования символов такого алфавита пятиразрядного кода уже недостаточно. Нужен как минимум 6-разрядный код. Поскольку 2 6 = 64, то остается еще резерв для 25 символов (64 — 39 = 25). Его можно использовать для кодирования цифр, всевозможных скобок, знаков математических операций и других символов, встречающихся в русском тексте. Следовательно, информационный вес символа в расширенном русском алфавите будет равен 6 битам. А текст из 1000 символов будет иметь объем 6000 битов.
Итак, если i —
информационный вес символа алфавита, а К 
количество символов в
тексте, записанном с помощью этого алфавита, то информационный объем I текста
выражается формулой:
I = К • i (битов).
Для определения информационного веса
символа полезно знать ряд целых степеней двойки. Вот как он выглядит в
диапазоне от 2 1 до 2 10 •
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
64 |
128 |
256 |
512 |
1024 |
Поскольку мощность лт алфавита может не являться целой степенью двойки, информационный вес символа алфавита мощности лт определяется следующим образом. Находится ближайшее к лт значение во второй строке таблицы, не меньшее N. СООТветствующее значение i в первой строке будет равно информационному весу символа.
О Пример. Определим информационный вес символа алфавита,
включающего в себя все строчные и прописные русские буквы (66); цифры (10); знаки препинания, скобки, кавычки (10). Всего получается 86 символов.
Поскольку 2 6 < 86 к: 2 7 , информационный вес символа данного алфавита равен 7 битам. Это означает, что все 86 символов можно закодировать семиразрядными двоичными кодами.
|
|
Теоретические основы информатики |
Для двоичного
представления текстов в компьютере чаще всего применяется восьмиразрядный код.
С помощью восьмиразрядного кода можно закодировать алфавит из 256 символов,
поскольку 256 = 28 . В стандартную кодовую таблицу (например,
используемую в ОС Windows таблицу ANSI) помещаются все необходимые символы:
английские и русские буквы — прописные и строчные, цифры, знаки препинания,
знаки арифметических операций, всевозможные скобки и пр.
Более крупной, чем бит, единицей измерения информации является байт: 1 байт = 8 битов.
О Информационный объем текста в памяти компьютера измеряется в байтах. Он равен количеству символов в записи текста.
Одна страница текста на листе формата А4 кегля 12 с одинарным интервалом между строками в компьютерном представлении будет иметь объем 4000 байтов, так как на ней помещается примерно 4000 знаков.
Помимо бита и байта, для измерения информации используются и более крупные единицы:
|
1 Кб (килобайт) |
— 210 байтов |
= 1024 байта; |
|
1 Мб (мегабайт) |
|
= 1024 Кб |
|
1 Гб (гигабайт) |
|
- 1024 Мб |
— 210
Объем рассмотренной страницы текста в килобайтах будет равен приблизительно 3,9 Кб. А книга из 500 таких страниц займет в памяти компьютера примерно 1,9 Мб.
В компьютере любые виды информации тексты, числа, изображения, звук —- преДставляются в форме двоичного коДа.
Объем информации любого вида, выраженный в битах, равен длине двоичного кода, в котором эта информация представлена.
|
Измерение информации |
|
 |
|
Измерение информации — алфавитный (объемный) подход |
|||||
|
Применяется в цифровых системах хранения и передачи информации |
|||||
|
Объем информации равен Длине Двоичного коДа Основная единица: 1 бит — один разряд двоичного кода |
|||||
|
Информационный вес символа (i би- тов) алфавита мощностью опреде- ляется из уравнения: 2' = М, где М — ближайшая к сверху целая степень двойки |
Информационный объем I текста, содержащего К символов: I = К • i битов, где i — информационный вес одного символа |
||||
|
Производные единицы |
|||||
|
Байт 1 байт = 6 |
Килобайт (Кб) 1 |
Мегабайт (Мб) 1 Мб = 1024 к |
Гигабайт (Гб) 1 Гб = |
Терабайт (Тб) 1024 Гб |
|
Вопросы и задания
1. Есть ли связь между алфавитным подходом к измерению информации и содержанием информации?
2. В чем можно измерить объем письменного или печатного текста? З. Оцените объем одной страницы данного учебника в байтах.
4. Что такое бит с позиции алфавитного подхода к измерению информации?
5. Как определяется информационный объем текста по А. Н. Колмого-
рову?
6. Какой информационный вес имеет каждая буква русского алфавита?
7. Какие единицы используются для измерения объема информации на компьютерных носителях?
|
О |
8. |
|
О |
9. Сколько символов
содержит сообщение, записанное с помощью |
|
О |
10. Сообщение занимает 2 страницы и содержит 1/16 Кб информации. На каждой странице 256 символов. Какова мощность используемого алфавита? 11. Возьмите страницу текста из данного учебника и подсчитайте информационные объемы текста, получаемые при кодировании его семиразрядным кодом и восьмиразрядным кодом. Результаты выразите в |
килобайтах и мегабайтах.
1 .2.2. Содержательный подход к измерению информации
Неопределенность знания и количество информации
Содержательный подход к измерению информации отталкивается от определения информации как содержания сообщения, получаемого человеком. Сущность содержательного подхода заключается в следующем: сообщение, информирующее об исходе какого-то события, снимает неопределенность знания человека об этом событии.
 |
Приведем примеры, иллюстрирующие данное
утверждение.
Ситуация 1. В ваш класс назначен новый учитель информатики; на вопрос «Это мужчина или женщина?» вам ответили: « Мужчина».
Ситуация 2. На чемпионате страны по футболу играли команды «Динамо» и «Зенит». Из спортивных новостей по радио вы узнаёте, что игра закончилась победой «Зенита».
Ситуация З. На выборах мэра города было представлено четыре кандидата. После подведения итогов голосования вы узнали, что избран Н. Н. Никитин.
Вопрос: в какой из трех ситуаций полученное сообщение несет больше информации?
Неопределенность знания это количество возможных вариантов ответа на интересующий вас вопрос. Еще можно сказать: возможных исходов события. Здесь событие — например, выборы мэра; исход — выбор, например Н. Н. Никитина.
В первой ситуации 2 варианта ответа: мужчина, женщина; во второй ситуации З варианта: выиграл «Зенит», ничья, выиграло «Динамо»; в третьей ситуации 4 варианта: 4 кандидата на пост мэра.
Согласно данному ранее определению, наибольшее
количество информации несет сообщение в третьей ситуации, поскольку
неопределенность знания об исходе события в этом случае была наибольшей.
|
информации определяется следующим обра- |
Клод Элвуд Шеннон |
|
зом. |
(1916-2001) |
В 40-х годах
ХХ века проблема измерения информации была решена американским ученым Клодом
Шенноном основателем теории информации. Согласно Шеннону, информация это снятая
неопределенность знания человека об исходе какого-то события.
В теории информации единица измерения
 |
Согласно этому определению, сообщение в первой из описанных ситуаций несет 1 бит информации, поскольку из двух возможных вариантов ответа был выбран один.
Следовательно, количество информации, полученное во второй и в третьей ситуациях, больше, чем один бит. Но как измерить это количество?
Рассмотрим еще один пример.
Ученик написал контрольную по информатике и
спрашивает учителя о полученной оценке. Оценка может оказаться любой: от 2 до
5. На что учитель ответил: «Угадай оценку за два вопроса, ответом на которые
может быть только «да» или «нет»». Подумав, ученик задал первый вопрос: «Оценка
выше тройки?». «Да», 
ответил учитель. Второй вопрос: «Это
пятерка?» «Нет» , ответил учитель. Ученик понял, что он получил четверку. Какая
бы ни была оценка, таким способом она будет угадана!
Первоначально неопределенность знания (количество возможных оценок) была равна четырем. С ответом на каждый вопрос неопределенность знания уменьшалась в 2 раза, и, следовательно, согласно данному выше определению одного бита, передавался 1 бит информации.
Первоначальные
варианты: 
|
|
|
4 |
5 |
Варианты, оставшиеся после 1-го вопроса (1 бит):
|
|
|||
|
|
|
4 |
|
Вариант, оставшийся после 2-го вопроса (+1 бит):
Узнав оценку (одну из четырех возможных), ученик получил 2 бита информации.
Рассмотрим еще один частный пример, а затем выведем общее правило.
Вы едете на электропоезде, в котором 8 вагонов, а на вокзале
вас встречает товарищ. Товарищ позвонил вам по мобильному телефону и спросил, в
каком вагоне вы едете. Вы предлагаете угадать номер вагона, задав наименьшее
количество вопросов, ответами на которые могут быть только слова «да» или
«нет».
Немного подумав, товарищ стал спрашивать:
— Номер вагона больше четырех?
— да.
|
|
Теоретические основы информатики |
 |
Номер
вагона больше шести?
— Нет.
— Это шестой вагон?
— Нет.
Ну теперь все ясно! Ты едешь в пятом
вагоне! Схематически поиск номера вагона выглядит так:
Первоначальные
варианты: 
|
|
|
|
|
5 |
|
|
|
После 1-го вопроса (1 бит):
|
|
|
|
|
5 |
6 |
|
|
После 2-го вопроса (+1 бит):
|
|
|
|
|
5 |
|
|
|
После 3-го вопроса (+1 бит):
Каждый ответ уменьшал неопределенность знания в два раза. Всего было задано три вопроса. Значит, в сумме набрано 3 бита информации. То есть сообщение о том, что вы едете в пятом вагоне, несет З бита информации.
Способ решения проблемы, примененный в примерах с оценками
и вагонами, называется методом половинного Деления: ответ на каждый вопрос
уменьшает неопределенность знания, имеющуюся перед ответом на этот вопрос,
наполовину. Каждый такой ответ несет 1 бит информации. 
Заметим, что решение подобных проблем методом половинного деления наиболее рационально. Таким способом всегда можно угадать, например, любой из восьми вариантов за 3 вопроса. Если бы поиск производился последовательным перебором: «Ты едешь в первом вагоне?» «Нет», «Во втором вагоне?» «Нет» и т. д., то про пятый вагон вы смогли бы узнать после пяти вопросов, а про восьмой после восьми.
«Главная формула» информатики
Сформулируем одно очень важное условие, относящееся к рассмотренным примерам. Во всех ситуациях предполагается, что все возможные исходы события равновероятны. Равновероятно, что учитель может быть мужчиной или женщиной; равновероятен любой исход футбольного матча, равновероятен выбор одного из четырех кандидатов в мэры города. То же относится и к примерам с оценками и вагонами.
Тогда полученные нами результаты описываются следующими формулировками:
|
Измерение информации |
|
 |
сообщение
об одном из четырех равновероятных исходов некоторого события несет 2 бита
информации; 
сообщение об одном из восьми
равновероятных исходов некоторого события несет З бита информации.
Обозначим буквой лт количество возможных исходов события, или, как мы это еще называли, — неопределенность знания. Буквой i будем обозначать количество информации в сообщении об одном из лл результатов.
В примере с учителем: = 2,
1
бит; в примере с оценками: лг = 4, i = 2 бита; в примере с вагонами: лт = 8, i
= З бита.
Нетрудно заметить, что связь между этими величинами выражается следующей формулой:
Действительно: 2 1 = 2; 2 2 = 4; 2 3 = 8.
С полученной формулой вы уже знакомы из курса информатики для 7 класса и еще не однажды с ней встретитесь. Значение этой формулы столь велико, что мы назвали ее главной формудой информатики. Если величина лт известна, а i неизвестно, то данная формула становится уравнением для определения i. В математике такое уравнение называется показательным уравнением.
Пример. Вернемся к рассмотренному выше примеру с вагонами. Пусть в поезде не 8, а 16 вагонов. Чтобы ответить на вопрос, какое количество информации содержится в сообщении о номере искомого вагона, нужно решить уравнение
16.
Поскольку 16 = 2 4 , получаем i = 4 бита.
Количество i информации, содержащееся в
сообщении об
О одном из лт равновероятных исходов некоторого события, определяется из решения показательного уравнения:
Пример, В кинозале 16 рядов, в каждом ряду 32 места. Какое количество информации несет сообщение о том, что вам купили билет на 12-й ряд, 10-е место?
Решение задачи: в кинозале всего 16 • 32 — 512 мест. Сообщение о купленном билете однозначно определяет выбор одного из этих мест. Из уравнения 2 i = 512 = 2 9 получаем: i = 9 битов.
 |
Данный пример иллюстрирует выполнение закона аДДитиво ности количества информации (правило сложения): количество информации в сообщении одновременно о нескольких результатах независимых друг от друга событий равно сумме количеств информации о кажДом событии отДельно.
Сделаем одно важное замечание. С формулой 2 i =
лт мы уже встречались, обсуждая алфавитный подход к измерению информации (см.
параграф 1.2.1). В этом случае лт рассматривалось как мощность
алфавита, а i — как информационный вес каждого символа алфавита. Если
допустить, что все символы алфавита появляются в тексте с одинаковой частотой,
т. е. равновероятно, то информационный вес i символа тождественен количеству
информации в сообщении о появлении любого символа в тексте. При этом лг —
неопределенность знания о том, какой именно символ алфавита должен стоять в
данной позиции текста. Данный факт демонстрирует связь между алфавитным и
содержательным подходами к измерению информации.
20
Формула Хартли
Если значение лт равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то показательное уравнение легко решить в уме, поскольку i будет целым числом. А чему равно количество информации в сообщении о результате матча «Динамо»—«Зенит»? В этой ситуации лт = З. Можно догадаться, что решение уравнения
будет дробным числом, лежащим между 1 и 2, поскольку 2 1 = 2 < З, а 22 = 4 > З. А как точнее узнать это число?
В математике существует функция, с помощью которой решается показательное уравнение. Эта функция называется логарифмом, и решение нашего уравнения записывается следующим образом:
log2N.
|
Измерение информации |
|
 |
log22= 1, logz 4 = 2, log2 З.
Значения логарифмов находятся с помощью специальных логарифмических таблиц. Также можно использовать инженерный калькулятор или табличный процессор. Определим количество информации, полученной из сообщения об одном исходе события из трех равновероятных, с помощью электронной таблицы. На рисунке 1.4 представлены два режима электронной таблицы: режим отображения формул и режим отображения значений.
|
|
|
|
||||
|
1 |
|
i битов |
||||
|
2 |
з |
=LOG |
|
|||
|
|
|
в |
|
||||
|
1 |
|
битов |
|
||||
|
2 |
з |
1 ,584962501 |
|
||||
Рис. 1.4. Определение количества информации в электронных таблицах с помощью функции логарифма
В
табличном процессоре Microsoft Excel функция логарифма имеет следующий вид:
основание). Аргумент значение находится в ячейке А2, а основание логарифма
равно 2. В результате получаем с точностью до девяти знаков после запятой:
i = log23 = 1,584962501 (бита).
Формула для измерения количества ин-
Ральф Хартли формации: = log2N была предложена амери(1888-1970) Канским ученым Ральфом Хартли — ОДНИМ из основоположников теории информации.
Формула Хартли:
i = log2N.
Здесь i — количество информации, содержащееся в сообщении об одном из лт равновероятных исходов события.
 |
Помимо рассмотренных нами двух
подходов к измерению информации (алфавитного и содержательного) в теории
информации известны и другие подходы. Выдающийся российский математик Андрей
Николаевич Колмогоров в 1965 году предложил свой подход к определению
количества информации, который получил название алгоритмического подхода. Суть
его в следующем. Владение информацией позволяет выбрать из некоторого исходного
множества альтернативных фактов (объектов) то иско-
|
Андрей |
мое подмножество, которое нас интересует, |
|
Николаевич |
т. е. удовлетворяет определенным критери- |
|
Колмогоров |
ям. Следовательно, информация выступает в |
|
(1903-1987) |
форме отношения между двумя множества- |
ми: исходным и искомым. По Колмогорову количество информации определяется как минимальная Длина программы, позволяющая однозначно преобразовать одно множество в Другое.
22
Система основных понятий
|
Измерение информации — содержательный подход |
|
|
Измеряется количество информации в сообщении об исходе некоторого события |
|
|
Равновероятные исходы: никакой результат не имеет преимущества перед другими |
|
|
Неопределенность знания — коли- чество возможных исходов события (вариантов сообщения) — лт |
Количество информации в сообщении об одном исходе события — i битов |
|
2i=N |
|
|
Частный случай: два равновероятных результата события |
|
|
|
i = 1 бит |
|
1 бит — количество информации в сообщении об одном из двух равновероятных исходов некоторого события |
|
|
Формула Хартли: i = log2 лт |
|
Вопросы и задания
1. Что такое неопределенность знания об исходе некоторого события?
2.
 |
З. Придумайте несколько ситуаций, при которых сообщение несет 1 бит информации.
4. В каких случаях и по какой формуле можно вычислить количество информации, содержащейся в сообщении, используя содержательный подход?
5. Сколько битов информации несет сообщение о том, что из колоды в 32 карты достали «даму пик»?
6.
При
угадывании методом половинного деления целого числа из диапазона от 1 до лг был
получен 1 байт информации. Чему равно N?
7. Проводятся две лотереи: «4 из 32» и «5 из 64». Сообщение о результатах какой из лотерей несет больше информации?
8. Используя формулу Хартли и электронные таблицы, определите количество информации в сообщениях о равновероятных событиях:
а) на шестигранном игральном кубике выпала цифра З;
б) в следующем году
ремонт в школе начнется в феврале;
в) я приобрел абонемент в бассейн на среду;
г) из 30 учеников класса
дежурить в школьной столовой назначили Дениса Скворцова.
9. Используя закон аддитивности количества информации, решите задачу о билете в кинотеатр со следующим дополнительным условием: в кинотеатре 4 зала. В билете указан номер зала, номер ряда и номер места. Какое количество информации заключено в билете?
О 1 .2.3. Вероятность и информация
Содержательный подход и вероятность
До сих пор речь шла о равновероятных исходах события. Но в реальности очень часто это предположение не выполняется. Интуитивно понятно, например, что для ученика-отличника получение пятерки и получение двойки неравновероятные исходы. Для такого ученика получить пятерку очень вероятный исход, а получение двойки маловероятно. Для двоечника же все наоборот.
|
|
Теоретические основы информатики |
 |
Предположим, мы посчитали, что за год по данному предмету ученик получил 100 оценок. Среди них: 60 пятерок, 25 четверок, 10 троек и 5 двоек. Тогда:
вероятность пятерки: 60/100 = 0,6; 
вероятность четверки: 25/100 = 0,25;
вероятность тройки: 10/100 = 0,1; 
вероятность двойки: 5/100 = 0,05.
Иногда удобно бывает вероятность выражать в процентах. Значение вероятности будем обозначать буквой Р. Тогда вычисленные нами величины запишем так:
Р5 = 0,6 (60 0/0); = 0,25 (25 0/0); Рз = 0,1 (10 0/0); Р2 = 0,05 (596).
Теперь, зная вероятности исходов события, можно определить количество информации в сообщении о каждом из них. Согласно теории информации, для этого нужно решить показательное уравнение
Вам уже известно, что его решение выражается через логарифм, и теперь оно выглядит так:
i = logA1/P).
Воспользуемся электронной таблицей и подсчитаем по этой формуле количество информации, содержащееся в сообщениях о получении нашим учеником каждой из оценок. Таблица приведена в режиме отображения формул и в режиме отображения значений (рис. 1.5).
|
|
|
в |
|
с |
|
|
||||||
|
1 |
ЦеНКа |
|
|
|
|
|
||||||
|
2 |
ероятность |
|
1 |
|
,25 |
|
||||||
|
з |
К-во информации (битов |
|
|
|
|
|
||||||
|
|
|
в |
с |
|
|
|
|||||||
|
1 |
ценка |
|
|
|
|
|
|||||||
|
2 |
ероятность |
|
|
|
|
|
|||||||
|
з |
-во информации (битов) |
,321928095 |
,321928095 |
|
, 736965594 |
|
|||||||
|
Измерение информации |
 |
Запишем
вычислительные формулы и полученные результаты с точностью до трех знаков после
запятой. log2(5/3) = 0,737 бита, log2(4) — 2 бита,
- log2(10) - 3,322 бита, — log2(20) — 4,322 бита.
Посмотрите внимательно на результаты, и вы увидите, что чем меньше вероятность события, тем больше информации несет сообщение о нем.
Количество информации в сообщении о некотором исходе события зависит от вероятности этого исхода. Чем меньше вероятность, тем больше информации.
На первый взгляд
кажется, что мы имеем две совсем разные формулы для вычисления количества
информации. Первая 
рез количество исходов событий, вторая —
через вероятность: 1) i - log2N; 2) i - logA1/P).
На самом деле это не разные формулы! Первая формула является частным случаем второй, в ситуации, когда вероятность исходов события оказывается одинаковой.
Представьте себе, что у нашего ученика было бы всех оценок поровну: пятерок, четверок, троек, двоек — по 25 штук. Тогда вероятность каждой оценки была бы равна 25/100 1/4. Значит, и количество информации было бы одинаковым. Посчитаем: i5 = i4 = i3 = i2 = log2 (1/0,25) = log2(4) = 2 бита,
Но это та же самая задача о четырех равновероятных оценках, которую мы решали раньше! И там тоже получалось 2 бита!
Приведем еще примеры сообщений об исходах события с разной вероятностью и сравним их информативность. Например, рассмотрим сообщения об осадках в зимнем прогнозе погоды. Зимой бывает снег, бывает отсутствие осадков и, очень редко, бывает дождь (во время сильной оттепели). Дождь зимой маловероятен. Поэтому зимой сообщение о дожде несет самую большую информацию.
 |
Информативность всех таких сообщений можно выразить в битах, если вычислить вероятности исходов события, обработав данные многолетних наблюдений.
Информационные веса символов алфавита и вероятность
А теперь рассмотрим, как с понятием вероятности связано вычисление информационных весов символов алфавита. Обсуждая алфавитный подход раньше, мы исходили из предположения, что появления в любой позиции текста символов используемого алфавита равновероятны. На самом деле для естественных языков это не так. Легко доказать, что одни символы встречаются чаще, а другие — реже, т. е. с разной частотой. Частота появления символа это отношение количества вхождений данного символа в текст к общему количеству символов в тексте. В таблице 1.1 приведены частотные характеристики букв латинского алфавита в английских текстах, а в таблице 1.2 русских букв (кириллицы) в текстах на русском языке (символ « » означает пробел). Эти данные получены путем усреднения результатов обработки большого числа текстов.
Таблица 1.1
Частотные характеристики букв латинского алфавита в английских текстах
|
Буква |
Частота |
Буква |
Частота |
Буква |
Частота |
Буква |
Частота |
|
Е |
0,130 |
|
0,061 |
|
0,024 |
к |
0,004 |
|
т |
0,105 |
н |
0,052 |
|
0,020 |
х |
0,0015 |
|
|
0,081 |
D |
0,038 |
У |
0,019 |
|
0,0013 |
|
о |
0,079 |
|
0,034 |
|
0,019 |
Q |
0,0011 |
|
N |
0,071 |
|
0,029 |
w |
0,015 |
z |
0,0007 |
|
R |
0,068 |
с |
0,027 |
в |
0,014 |
|
|
|
1 |
0,063 |
м |
0,025 |
|
0,009 |
|
|
Таблица 1.2
Частотные характеристики русских букв (кириллицы)
|
Измерение информации |
|
 |
|
Буква |
Частота |
Буква |
Частота |
Буква |
Частота |
Буква |
Частота |
|
пробел |
0,175 |
|
0,040 |
я |
0,018 |
х |
0,009 |
|
о |
0,090 |
в |
0,038 |
ы |
0,016 |
ж |
0,007 |
|
|
0,072 |
л |
0,035 |
з |
0,016 |
ю |
0,006 |
|
|
0,062 |
к |
0,028 |
|
0,014 |
ш |
0,006 |
|
и |
0,062 |
м |
0,026 |
Б |
0,014 |
ц |
0,003 |
|
т |
0,053 |
д |
0,025 |
|
0,013 |
щ |
0,003 |
|
н |
0,053 |
п |
0,023 |
|
0,013 |
Э |
0,003 |
|
с |
0,045 |
|
0,021 |
й |
0,012 |
ф |
0,002 |
Как видно из этих таблиц, наиболее часто употребляемая бук-
ва в английском тексте «Е», а наименее
«популярная» 
«ь. Соответственно в русском тексте это
буквы «О» и «Ф».
По аналогии с тем, что было рассмотрено выше, вам должно быть понятно, что частота встречаемости буквы связана с вероятностью ее появления в определенной позиции текста. Чем частота больше, тем больше вероятность. Следует иметь в виду, что величина частоты, вычисленная по тексту конечного размера, дает оценочное (приближенное) значение вероятности. С увеличением размера текста эта оценка становится всё ближе к точному значению вероятности — Р. Отсюда следует, что информационный вес символа вычисляется по формуле:
i = logA1/P).
По этой формуле для русской буквы «О»
получаем: i
= 
= 3,47 бита. А для буквы «Ф»: i
== 8,97 бита. Разница весьма существенная! Принцип прежний: чем меньше вероятность, тем больше информации.
Для
оценки средней информативности символов алфавита 
с учетом разной
вероятности их встречаемости используется формула Клода Шеннона:
|
|
Теоретические основы информатики |
 |
В частном случае равной вероятности, когда
формула Шеннона переходит в формулу Хартли (докажите это самостоятельно).
Воспользовавшись данными из таблиц 1.1 и 1.2, по формуле Шеннона можно определить среднюю информативность букв алфавита английского и русского языков. Результаты вычислений для английского языка дают величину 4,09 бита, а для русского — 4,36 бита. При допущении, что все буквы встречаются с равной вероятностью, по формуле Хартли получается для английского языка Нангл log226 4,70 бита, а для русского языка — нрус = log232 = 5 битов. Как видите, учет различия частоты встречаемости букв алфавита приводит к снижению их средней информативности.
Из полученных результатов следует, что и полный информационный объем текста будет разным, если для его вычисления использовать формулы Хартли и Шеннона. Например, текст на русском языке, состоящий из 1000 букв, по Хартли будет содержать 5 1000 5000 битов информации, а по Шеннону: 4,36 • 1000 =
 |
|
Вероятность и информация |
|
|
Вероятность некоторого исхода события измеряется частотой его повторений для большого числа событий (в пределе стремящемся к бесконечности) |
|
|
Содержательный подход |
Информационные веса символов алфавита |
|
Р — вероятность определенного исхода события, п — количество повторений события (большое число), К — количество повторений данного исхода |
Р — частота встречаемости символа в тексте, п — размер текста в символах, К — количество вхождений данного символа в текст |
|
i log2(1/P) i (битов) количество информации в сообщении об исходе события, вероятность которого равна Р |
i log2(1/P) i (битов) — информационный вес символа, частота встречаемости которого (вероятность) равна Р |
|
|
Формула Шеннона: Н = P110gA1/P1) + P210g2(1/P2) + + PNlogA1/PN). Н — средняя информативность символа алфавита, РК — вероятность появления символа номер К, — размер алфавита |
Вопросы и задания
1. Как можно оценить вероятность исхода события?
2. Как определяется информативность сообщения о некотором исходе события с вероятностной точки зрения?
З. Синоптики подсчитали, что в течение 100 лет 10 марта было 34 дождливых дня, снег выпадал 28 раз и 38 дней было без осадков. Определите количество информации в сообщениях, что 10 марта текущего года: будет снег; будет дождь; осадков не будет. Для расчета используйте электронные таблицы.
4. В корзине лежат 8 черных шаров и 24 белых шара. Какое количество информации несет сообщение о том, что достали черный шар?
5. В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар, несет 2 бита информации. Сколько всего шаров в корзине?
6. На остановке останавливаются автобусы разных маршрутов. Сообщение о том, что к остановке подошел автобус 5-го маршрута, несет 4 бита информации. Вероятность появления на остановке автобуса 10-го маршрута в два раза меньше, чем вероятность появления автобуса 5-го маршрута. Какое количество информации несет сообщение о появлении на остановке автобуса 10-го маршрута?
7. Как определяется информационный вес символа алфавита с вероятностной точки зрения?
8.
Подсчитайте
информационный объем слова ИНФОРМАТИКА, используя для вычисления информационных
весов символов формулу 
log2(1/P) и данные из табл. 1.2. Вычисления проведите с помощью
электронной таблицы.
9. Подсчитайте информационный объем слова ИНФОРМАТИКА, используя значение средней информативности символов русского алфавита, вычисленное по формуле Шеннона с учетом равной вероятности: Н 5 битов. Сравните с результатом предыдущей задачи. Попробуйте объяснить расхождение.
|
|
Теоретические основы информатики |
 |
Системой счисления или нумерацией называется определенный способ записи чисел. Из курса информатики 7—9 классов вы знакомы с историей систем счисления, знаете, что бывают позиционные и непозиционные системы счисления. Вам также известно, что привычная для нас система счисления называется десятичной позиционной системой, что в компьютере для представления чисел и выполнения вычислений используется двоичная система счисления.
Числа несут в себе количественную информацию. Запись чисел поисходит по правилам определенной системы счисления. От выбора системы счисления зависит длина числа, т. е. количество цифр в записи числа, а также правила выполнения вычислений. Одна из главных проблем, которую нужно было решить изобретателям ЭВМ, это представление чисел в памяти ЭВМ и алгоритм их обработки (вычислений) процессором. Для понимания того, как была решена эта проблема, нужно знать принципы организации систем счисления.
Основные понятия позиционных систем счисления
О Цифра символ, используемый для записи чисел,
Алфавит системы счисления совокупность всех цифр.
Каждая позиция в
записи числа называется разрядом числа. Разряды нумеруются в целой части числа
положительными целыми числами, начиная с нуля, в дробной части — отрицательными
числами, начиная с —1:
разряды: з 2 1 о -1-2-3 число: 6248, 5 4 7
Здесь номера разрядов указаны маленькими цифрами
сверху. В записи многозначного числа цифры, стоящие в разных позициях, имеют
разные веса. Так, в целом десятичном числе 325 тройка означает три сотни,
двойка два десятка, пятерка 
пять единиц: 325 = З • 100 + 2 • 10 + 5 '
1. Такая запись называется развернутой формой записи числа: число записывается
в виде суммы, в которой каждое слагаемое — это цифра, умноженная на свой вес.
Вот еще пример развернутой записи смешанного десятичного числа:
6248,547
= 103 + 2- 102 + 10 1 + 8 - 100 + 5• 10-1 + 10-2 + 7 • 1 -3 .
|
Системы счисления |
|
 |
Следующий, бесконечный в обе стороны ряд целых степеней
десяти называется базисом десятичной системы счисления:
109 , 108 , 10 7 , 106 , 10 5
, 104 , 103 , 102 , 10 1 , 100
, 10-1 , 10-2 , 10-3 ,
Запись числа в развернутой форме еще называют разложением числа по базису.
Десятичная система относится к числу традиционных систем счисления. Для традиционных систем счисления принято размерность алфавита называть основанием системы счисления. Основание десятичной системы счисления равно десяти.
По такому же принципу организованы все другие традиционные системы счисления. Наименьшим основанием для позиционных систем является 2 (двоичная система). Система с основанием 1 не может быть позиционной, поскольку для нее невозможно построить базис (все веса одинаковы) единица в любой степени равна единице. Базис двоичной системы счисления выглядит (в десятичной записи) так:
2 9 , 2 8 2 7 2 6 2 5 2
4 2 3 2 2 2 1 2 0 2 -1 2
-2 2 -3
Основанием традиционной системы счисления может быть любое натуральное число, начиная с 2, а базис бесконечный в обе стороны ряд целых степеней основания.
О нетрадиционных системах счисления поговорим позже.
Вот несколько примеров позиционных систем и их алфавитов:
|
Основание |
Название |
Алфавит |
|
2 |
Двоичная |
0 1 |
|
з |
Троичная |
0 1 2 |
|
8 |
Восьмеричная |
0 1 2 34 5 6 7 |
|
16 |
Шестнадцатеричная |
О 1 2 З 4 5 6 7 8 9 А В С D Е F |
Если п основание системы, не большее десяти, то в алфавите используются п первых арабских цифр. Если основание превышает 10, то в качестве дополнительных цифр выступают буквы латинского алфавита по порядку.
|
|
Теоретические основы информатики |
|
32 |
 |
В любой позиционной системе счисления число, количественно равное ее основанию, записывается как 10. При этом только в десятичной системе оно читается как «десять». Во всех других системах следует читать «один, ноль».
Например: 102 = 2, 103 - з, 108 = 8, 1016 — 16 и т. д.
Задача 1. Число в троичной системе счисления 2011,13 перевести в десятичную систему.
Решение. Разложим данное число по базису троичной системы счисления, т. е. запишем его в развернутой форме, и вычислим полученное выражение по правилам десятичной арифметики:
2011,13 = 2-33 + + 1-3 1 + + 1-3 -1 = 54 +3+ 1 + 1/3 = 58 2 з.
Задача 2. Шестнадцатеричное число 2AF,8C16 перевести в десятичную систему.
Решение. Задача решается аналогично задаче 1 через разложение шестнадцатеричного числа по базису системы счисления и вычисление полученного выражения. В записи разложения цифры, обозначаемые буквами, заменяются на их эквиваленты в десятичной системе.
2AF,8C16 2 • 16 2 + 10 •
16 + 15 • 160 + 8 • 16-1 + 12 16 -2 = 
= 512 + 160 + 15 + 1/2 + 3/64 = 687,546875.
сятичную систему.
Решение
+ + 1 + 1-2 -1 + 1-2 -5 + 512 + 128 + 32 + + 8 + 4 + 2 + 1 +1/2 + 1/32 + 1/64 687,546875.
Обратите внимание, что результат тот же, что и в
задаче 2. Значит, двоичное число из данной задачи равно шестнадцатеричному
числу из задачи 2. К этому обстоятельству мы еще вернемся. 
Схема Горнера и перевод чисел
 |
|||
 |
|||
2317458 - 2 . 85 + З . 84 + 1 . 83 + 7 , 82 + 4 . 8 + 5 _
= • 8 + 3) • 8 + 1) 8 + 7) • 8 + 4) 8 + 5 =
7882110.
Скобочное выражение очень просто вычислять. На калькуляторе нужно последовательно слева направо выполнять умножения и сложения. Порядок нажатия клавиш на калькуляторе будет таким:
В калькуляторе реализуется алгоритм последовательного выполнения цепочки операций: при нажатии клавиши со знаком операции выполняется предыдущая операция и ее результат высвечивается на индикаторе. После нажатия клавиши «равно» выполняется последняя операция цепочки и на индикаторе отражается результат вычисления всего выражения. В расмотренном примере было выполнено пять умножений и пять сложений. Такой способ вычисления называется схемой Горнера.
В общем виде алгебраический многочлен п-й степени и его
преобразование к скобочной форме выглядят так: апхп + ап_1хП-
1 + ... + а2Х2 + а1Х + ао
= ((...((апх + + + ... + 02)x + а1)х + ао.
Из этой формулы следует, что алгебраический многочлен п-й степени можно вычислить за п операций умножения и п операций сложения. Это самый оптимальный способ вычисления.
Схему Горнера можно применить и для перевода дробных чисел. Покажем это на примере двоичного числа 0,1101012. Запишем число в развернутой форме и выполним тождественные преобразования, приводящие выражение к скобочной форме:
0,1101012 1 • 2 -1 + 1 • 2-2 + о • 2 -3 + 1 • 2 -4 + 0 • 2-5 + 1 • 2-6 =
= 1 • 2-6 + 0 • 2 -5 + 1 • 2-4 + 0 • 2-3 + 1 • 2 -2 + 1 • 2 -1 =
= (((((1/2 + 0)/2 + 1)/2 + 0)/2 + 1)/2 + 1)/2 о, 828125.
|
за |
|
|
Теоретические основы информатики |
 |
сложения. Клавиши нажимаются в таком порядке:
Прибавление нулей можно не делать, тогда число операций сложения сократится до трех:
Пример нетрадиционной системы счисления
В качестве примера нетрадиционной системы счисления рассмотрим так называемую Фибоначчиеву систему. Алфавит Фибоначчиевой системы состоит из двух цифр: О и 1, как у двоичной системы счисления. Базисом этой системы является следующий числовой ряд: 1, 2, З, 5, 8, 13, 21, 34, 55, 89 Он называется рядом Фибоначчи, или числами Фибоначчи. Ряд Фибоначчи строится следующим образом. Первые два числа: F1 = 1, F2 = 2. Каждое следующее число равно сумме двух предыдущих чисел:
Можно доказать, что в Фибоначчиевой системе представимо любое целое число. В таблице 1.3 для сравнения приводятся первые 10 целых чисел в десятичной, двоичной и Фибоначчиевой системах счисления.
Таблица 1.3
Представление чисел в Фибоначчиевой системе счисления
|
есятичная с. с. |
|
|
|
|
|
|
|
|
|
|
|
воичная с. с. |
о |
1 |
10 |
11 |
100 |
101 |
110 |
111 |
1000 |
1001 |
|
Фибоначчиева с. с. |
о |
1 |
10 |
100 |
101 |
1000 |
1001 |
1010 |
10000 |
10001 |
Отметим важную особенность Фибоначчиевой системы: неод-
|
Системы счисления |
|
 |
Система основных понятий
|
Позиционные системы счисления |
|
|
Традиционные системы: основание системы (р) равно размеру алфавита; базис — бесконечный в обе стороны ряд целых степеней основания |
|
|
Развернутая форма записи числа: + + ао2 + ар + ао + a_w-1 + + а_пр—т — цифра i-I'0 разряда числа; р — основание системы счисления 22 |
|
|
Схема Горнера — быстрый алгоритм перевода р-ичного числа в десятичное |
|
|
Целое число |
Дробное число |
|
+ аз)р + адр + ат)р + ао |
|
|
Нетрадиционная система (пример): Фибоначчиева система счисления |
|
|
Базис:
|
Алфавит: |
|
Фибоначчиева система счисления избыточна; традиционные системы не избыточны |
|
Вопросы и задания
1.
Определите
основные понятия систем счисления: традиционные системы, нетрадиционные
системы; цифра, алфавит системы, основа
ние системы. 
2. Почему развернутую форму записи числа называют разложением по базису?
З. Чему будет равно: 1/3 при переводе в троичную систему, 1/5 — в пятеричную систему, 1/8 — в восьмеричную систему, 1/16 — в шестнадцатеричную систему?
4. Что общего между результатами
вычисления следующих выражений: 
1112 + 12, 2223 + 13, 7778 + 18, FFF16 + 116?
О 5. Назовите предыдущие
значения в натуральном ряде чисел для следу
ющих значений: 1005, 1007, 1009
6.
Выполните быстрый
перевод в десятичную систему счисления сле
дующих недесятичных чисел, пользуясь калькулятором и
вычислительной схемой Горнера:
а) 32045, 11010112,
567218, 9A3CEF16; 
6) 0,32045, 0,11010112, 0,567218, 0,9A3CEF16.
7. В таблице 1.3 для всех чисел в диапазоне от О до 9 приведено лишь по одному способу представления в Фибоначчиевой системе счисления. Для тех чисел из таблицы, представление которых неоднозначно, запишите все варианты.
|
|
Теоретические основы информатики |
Практикум. Раздел 1 «Системы счисления»
1 .3.2. Перевод десятичных чисел в другие системы счисления
Рассмотрим перевод десятичных чисел в системы счисления с другими основаниями. Подойдем к этой проблеме с общей математической позиции.
Сначала получим правило перевода целого числа. Обозначим О целое число через Х. Основание системы счисления, в которую будем переводить, обозначим р. В результате перевода получится (п + 1)-разрядное число. Запишем это следующим образом:
Здесь ао обозначает цифру нулевого разряда числа, — цифру первого разряда и т. д. Значения этих цифр лежат в диапазоне от О до р— 1. Запишем значение числа в системе с основанием р в развернутом виде и преобразуем в скобочную форму:
+ ап-1)р + ап-2)р +
Отсюда нетрудно понять, что ао равно остатку от
целочисленного деления Х на р, а Х 1 частное от целочисленного деления Х на р.
Применяя символику языка Паскаль, запишем: ао — 
Х mod р, Х 1 Х div р.
Здесь div знак операции целочисленного деления, а mod знак операции остатка от
деления. Таким образом, найдена ао цифра нулевого разряда числа в р-ичной
системе.
Теперь запишем число Х 1 в скобочной форме:
= 
+ а1 = Х2 • р + ат.
По аналогии с предыдущим: = Х 1 mod р остаток от деления Х 1 на р; Х2 = Х 1 div р. Найден — первый разряд искомого числа.
Продолжая далее целочисленные деления на р с выделением остатка, последовательно будем получать искомые цифры р-ичного числа. Процесс закончится, когда в результате деления нацело (div) получится ноль. Последний остаток будет равен ап— старшей цифре числа.
|
|
37 |
 |
58 : з = 19 (1)
(1)
Запишем последовательно остатки, начиная с
последнего: 
58 20113. Это равенство мы уже получали в
предыдущем параграфе.
Теперь рассмотрим перевод десятичной дроби в систему счисления с основанием р. Пусть У — дробное десятичное число: У < 1. Очевидно, что в системе с основанием р оно также будет дробным числом, поскольку 1 в любой системе счисления обозначает одну и ту же величину. Число, равное У в системе с основанием р, запишем в развернутой форме:
У = 
= а_р-1 + а_2р-2 + а_зр-з +
Умножим это равенство на р:
У • р = а_1 + а_2р-1 + а_зр-2 +
Отсюда видно, что это целая часть
произведения У • р, а У1 — дробная часть этого произведения. Далее умножим У1
на р: У 1 •р = а_2 + а_зр-1 + а_ар-2 +
Теперь стало целой частью произведения У1 • р. Очевидно, что дальше нужно умножать на р значение У2. Выделив его целую часть, получим третью цифру дробного числа — а_з. И так далее.
До каких же пор продолжать этот процесс? Тут могут быть разные ситуации. Первая ситуация: после некоторого числа умножений в дробной части произведения получится ноль. Понятно, что все следующие ај будут равны нулю. Следовательно, переведенное значение имеет конечное число цифр. Рассмотрим пример такого перевода.
Задача 2. Перевести десятичную дробь 0,625 в двоичную систему счисления.
Будем последовательно умножать это число на 2, выделяя
целую часть произведения:
0,625 • 2 1,25 1 — первая цифра
0,25 • 2 - 0,5 о — вторая цифра
 |
Дальше нули В итоге получили: 0,62510 -
0,1012.
Вторая ситуация получение периодической дробной части. В таком случае последовательные умножения надо продолжать до выделения периода.
Задача 3, Перевести число 0,24610 в пятеричную систему счис-
ления.
0,246
1,23 1
0,23
1,15 1
0,15
0,75 о
0,75
3,75 з
0,75
3,75 з
Далее пойдет периодическое повторение цифры З. Результат получился таким:
0,24610
Из математики вам должно быть известно, что число с конечной или периодической десятичной дробной частью является рациональным. Можно доказать, что любое дробное рациональное десятичное число при переводе в другую систему счисления также дает рациональное число. Попробуйте доказать это самостоятельно!
Чаще всего при переводе десятичной дроби в другую
систему счисления получают приближенный результат с заданной точностью.
Например, пусть требуется перевести десятичное число 0,21 в восьмеричную
систему счисления с точностью до 7 цифр. Выполняется перевод числа до 8 цифр
после запятой: 0,2110
0,15341217 8 Затем
производится округление до 7-й цифры: 
0,15341228. Заметим,
что в этом случае к последней цифре нужно прибавлять единицу, если первая
отбрасываемая цифра 
4, так как 8/2 = 4.
Если требуется перевести смешанное десятичное число, то отдельно переводится целая часть числа путем последовательных делений и отдельно дробная часть числа путем умножений. Затем два этих результата записываются через запятую одним смешанным числом.
Вопросы и задания
1.
Как переводится
целое десятичное число в систему счисления с осно ванием р?
|
Системы счисления |
|
2.
 |
З. Переведите число 4267,13 в двоичную и восьмеричную системы счисления.
1 .З.З. Автоматизация перевода чисел
В этом параграфе будут рассмотрены способы перевода чисел из одной системы счисления в другую с помощью электронных таблиц и программирования.
Перевод из недесятичной системы в десятичную
Как переводить недесятичные числа в десятичную систему счисления, было рассказано раньше. Там же был описан способ быстрого перевода на основе использования схемы Горнера, который можно реализовать на простом калькуляторе.
Решим теперь такую задачу. Требуется создать электронную таблицу, с помощью которой будет производиться автоматический перевод недесятичного числа из любой системы счисления, основание которой меньше десяти, в десятичную систему.
Пример использования такой таблицы приведен на рис. 1.6.
Здесь показан перевод троичного числа 2011,13
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Основание системы: |
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
Разряды: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
Число: |
|
|
2 0 |
1 |
1 |
|
|
|
|
|
= |
58,333333 |
|
|
Б |
Перевод: |
0 0 54 0 3 1 |
|
0,33 |
о |
о |
о |
|
|
|||||
Рис. 1 .б. Перевод недесятичного числа в десятичную систему счисления в электронной таблице
Для перевода числа используется разложение его по базису.
Основание системы — в ячейке Т. Номера разрядов числа равны степеням основания
в базисе (в развернутой форме). Значащие цифры числа вписываются в
соответствующие ячейки пятой строки. В шестой строке вычисляются слагаемые
развернутой формы числа. Например, в ячейке Вб записана формула:
В ячейке Сб: 
и т. д. Результат
перевода получается в ячейке М, где стоит формула: =CYMM(B6:L6). Данная таблица
рассчитана на 6-разрядную целую часть и 4-разрядную дробную часть. При
необходимости ее можно расширить.
Учимся программировать
(целочисленная арифметика)
 |
Program Numbers р 10; Var N10, Np, К: 10ngint;
begin
Write ( 'р= ' ) ; Readln (р) ; ввод основания системы}
Write('N', р, ; Read1n (Np) ; {ввод исходного р—ичного числа у
while do 4 ЦИКЛ
выполняется, пока Np не равно нулю) begin
: =NIO+ (Np mod 10) *
К; [суммирование развернутой формы}
К:=К*р; (вычисление базиса: р, р в степени 2, . . . }
Np : div 10 отбрасывание младшей
цифры) end ;
Write1n(
N10) вывод десятичного ЧИСЛО end.
В программе использованы следующие переменные:
основание системы
счисления исходное данное; лтр целое р-ичное число исходное данное; N10
десятичное число — результат.
Тип 10ngint тип длинное целое. Значения величин этого типа лежат в диапазоне от —2147483648 до 2147483647. (Значит, данная программа может работать с числами, не более чем 9-значными.) Тип переменной р — диапазон целых чисел от 2 до 9.
|
Системы счисления |
|
 |
целочисленное деление,
mod остаток от целочисленного деления. Например: 1234 mod 10 4 выделяется
разряд единиц; 1234 div 10 123 — отбрасывается младший разряд.
Пример, При переводе по данной программе двоичного числа 11012 в десятичную систему на экране увидим:
р=2 N2=1101
ГИ 0=13
Следовательно, в итоге получили: 11012 1310.
Для лучшего понимания работы программы внимательно изучите приведенную ниже трассировочную таблицу. Она отражает изменения значений переменных на каждом шаге выполнения алгоритма, реализованного в программе.
|
Шаг алго итма |
Команда алгоритма |
Р |
лтр |
|
N10 |
Проверка словия |
|
|
1 |
Ввод р, НР, К :=1, N10=O |
2 |
1101 |
1 |
|
|
|
|
2 з |
|
|
|
|
|
1101 * о, да |
|
|
4 |
(NP mod |
10) |
|
|
2 |
1 |
|
|
5 |
Np : =Np div 10 |
|
|
110 |
|
|
|
|
6 |
|
|
|
|
|
|
110 О, да |
|
7 |
N10 (Np mod |
10) |
|
|
|
1 |
|
|
8 |
|
|
|
|
4 |
|
|
|
9 |
Np: div 10 |
|
|
11 |
|
|
|
|
10 11 |
|
|
|
|
|
|
11 О, да |
|
12 |
(Np mod К:=К*р |
10) |
|
|
8 |
5 |
|
|
13 |
div 10 |
|
|
1 |
|
|
|
|
14 15 |
Np<>O : |
|
|
|
|
|
1 * О, да |
|
16 |
N10 mod |
|
|
|
16 |
13 |
|
|
17 |
Np: div 10 |
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
О О, нет |
|
19 |
Вывод N10 |
|
|
|
|
13 |
|
Теперь познакомьтесь с программой перевода целого десятичного числа в недесятичную систему счисления с основанием р (1 10).
Program Numbers1 О—р;
Var N10, Np, К: 10ngint; р: 2. .9; begin
Read1n (N10) ; (Ввод исходного
10—тичного числа
Write ( 'р=' ) ; Read1n (р) ; (Ввод основания системы)
К: =1; Np:=O; repeat
Np:=Np+ (N10 mod р) * К; Суммирование развернутой формы)
Вычисление базиса: 10, 100, 1000 
div р { Отбрасывание младшей цифры} until (N10=0) , (Цикл заканчивает
выполнение при NIO=O
|
|
Теоретические основы информатики |
 |
{Вывод р—ичного числа} end.
Здесь использованы те же обозначения, что
и в предыдущей программе. Исходными данными являются: N10 десятичное число и р
основание системы, в которую осуществляется перевод. Результат получается в
переменной Np — число в системе с основанием р.
В алгоритме используется цикл с постусловием repeat.
until. Цикл повторяется до выполнения условия: N10 = О.
Пример использования программы. Переведем число 2510 в двоичную систему счисления. Работа программы на экране компьютера отразится следующим образом:
N10=25 р=2
N2=11001
Следовательно, в результате получим: 25 =110012.
Для лучшего понимания работы программы рекомендуем построить трассировочную таблицу наподобие предыдущей.
Система основных понятий
|
Перевод десятичных чисел в р-ичные |
|
|
Целые числа |
Дробные числа |
|
Перевод производится последовательным делением числа нар с выделением остатка. Вычисление заканчивается, когда частное становится равным нулю |
Перевод производится последовательным умножением числа на р с выделением целой части произведения. Результат конечная или периодическая дробь |
|
Программирование перевода 10 —» р и р 10 основано на использовании операций над целыми числами: div — целочисленное деление, mod остаток от целочисленного деления. |
|
Практикум. Раздел 1 «Системы счисления» 
1 .3.4. Смешанные системы счисления
|
Системы счисления |
|
 |
Примером смешанной системы является двоично-десятичная система счисления. В ней десятичное число записывается путем замены каждой цифры на 4-разрядный двоичный код. Таблица соответствия для двоично-десятичной системы следующая:
|
10 |
|
|
|
|
|
|
|
|
|
|
|
2 |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
1000 |
1001 |
В этой таблице каждой десятичной цифре поставлено в
соответствие равное ей четырехзначное двоичное число (нули слева незначащие).
Например, десятичное число 58236,37 в двоично-десятичной форме запишется так:
1011000 0010 00110110,001101112 10 
Первый слева ноль у целого числа является
незначащей цифрой, поэтому его можно не писать.
Для обратного преобразования из двоично-десятичной формы в десятичное число нужно разбить на четверки все знаки двоичного кода: от запятой влево в целой части и вправо в дробной части. Затем каждую четверку двоичных цифр заменить на соответствующую десятичную цифру. Например:
11 1000 0010 1001 0011,0101 1001 1000 2_10 38293,598.
Отметим важное обстоятельство: между данными десятичным и
двоично-десятичным числами нельзя поставить знак равенства! Двоично-десятичное
представление это всего лишь двоичный код для представления десятичного числа,
но никак не равное ему значение в двоичной системе счисления. Выполнение
арифметических вычислений над десятичными числами, представленными в двоично-десятичной
форме, весьма затруднительно. Тем не менее в истории ЭВМ известны такие
примеры. В первой ЭВМ под названием ENIAC использовалась двоично-десятичная
система.
Современные компьютеры производят вычисления в двоичной системе счисления. Однако для представления компьютерной информации нередко используются двоично-восьмеричная и двоичношестнадцатеричная системы.
Двоично-восьмеричная система счисления. В следующей
таблице представлено соответствие между восьмеричными цифрами и трехзначными
двоичными числами (двоичными триадами), равными по значению этим цифрам: 
|
8 |
о |
1 |
2 |
з |
4 |
5 |
6 |
7 |
|
2 |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
|
Теоретические основы информатики |
 |
это значит заменить
каждую восьмеричную цифру на соответствующую двоичную триаду. Например:
3517,28 11 101 001
А теперь переведем данное восьмеричное число в двоичную систему счисления. Для этого сначала его переведем в десятичную систему, а потом из десятичной системы в двоичную. Вот что получается:
Но это тот же самый двоичный код, что записан выше в двоично-восьмеричной системе! Мы пришли к следующему результао ту: Двоично-восьмеричное число равно значению Данного восьмеричного числа в двоичной системе счисления.
Отсюда следует, что перевод чисел из восьмеричной системы счисления в двоичную производится перекодировкой по двоичновосьмеричной таблице путем замены каждой восьмеричной цифры на соответствующую двоичную триаду. А для перевода числа из двоичной системы в восьмеричную его цифры надо разбить на триады (начиная от запятой) и заменить каждую триаду на соответствующую восьмеричную цифру.
Двоично-шестнадцатеричная система счисления. В следующей таблице представлено соответствие между шестнадцатеричными
цифрами и четырехзначными двоичными числами (двоичными тетрадами), равными по значению этим цифрам:
|
16 |
|
1 |
2 |
з |
4 |
5 |
6 |
7 |
|
|
2 |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
|
|
16 |
8 |
9 |
|
в |
С |
D |
|
|
|
|
2 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
|
|
Записать шестнадцатеричное число в двоично-шестнадцатеричном виде это значит заменить каждую шестнадцатеричную цифру на соответствующую двоичную тетраду. Например:
Переведем данное шестнадцатеричное число сначала в десятичную систему счисления, а затем в двоичную систему. Получим:
Получился тот же самый двоичный код, что записан выше в двоично-шестнадцатеричной системе! Рассмотренный пример привел к следующему результату: Двоично-шестнадцатеричное число равно значению Данного шестнадцатеричного числа в двоичной системе счисления.
 |
Можно ли на основании приведенных частных примеров
делать глобальные выводы о том, что двоично-восьмеричный
(двоично-шестнадцатеричный) код любого восьмеричного (шестнадцатеричного) числа
совпадает с двоичным значением этого числа? Нет, конечно! Это утверждение
требует доказательства. Такое доказательство существует»
Доказано, что для любого числа в системе счисления с основанием р = 2 п смешанный Двоично-р-ичный код совпаДает с представлением этого числа в двоичной системе счисления.
Поскольку 8 = 2 3 , а 16 = 2 4 , сформулированное правило относится к восьмеричной и шестнадцатеричной системам. Очевидно, что такая же связь существует между двоичной и четверичной системами счисления, поскольку 4 2 2 .
Любые данные в памяти компьютера хранятся в двоичном виде.
1 ) См. АнДреева Е. В., Босова Л. Л., Фалина И. Н. Математические основы информатики. Элективный курс. — М.: БИНОМ. Лаборатория знаний, 2007.
Восьмеричную и шестнадцатеричную системы счисления используют для компактной записи содержимого памяти компьютера, а также записи ее адресации. Восьмеричное представление сжимает двоичный код в три раза, а шестнадцатеричное
Зддачд, Перевести число 1369,75 в двоичную, восьмеричную и шестнадцатеричную системы счисления.
Решение. Наиболее рациональный способ решения задачи следующий. Нужно перевести это число в одну из трех систем с основанием 2, 8 или 16, а затем, используя связь между ними через смешанное представление, выполнить перевод в две другие системы путем перекодировки по таблицам 2—8 и 2—16.
|
|
Теоретические основы информатики |
1.
 |
2. Путем перекодировки по двоично-восьмеричной таблице переведем это число в двоичную систему счисления: 2531,68 - 10 101 011 001,1102.
З. Разделив цифры двоичного числа на тетрады (влево и вправо от запятой), переведем двоичное число в шестнадцатеричную систему, используя двоично-шестнадцатеричную таблицу: 0101 0101 1001,11002 559,C16.
Система основных понятий
|
Смешанные системы счисления |
||
|
Число в системе с основанием q записывается цифрами из алфавита системы с основанием р |
||
|
Двоичнодесятичная У2_10 |
Двоичновосьмеричная
|
Двоично- шестнадцатеричная Х16 У2-16 |
|
1 десятичная цифра —» 4 двоичные цифры |
1 восьмеричная цифра З двоичные цифры У2_8 = У2 = Х8 |
1 шестнадцатеричная цифра 4 двоичные цифры У2_16 У2 = |
|
Известны примеры использования для представления в компьютере десятичных чисел |
Используются для записи сжатого представления двоичных данных и записи адресов памяти компьютера |
|
Вопросы и задания
1. Дайте определение смешанной системы счисления.
2. Почему двоично-десятичный код не совпадает с двоичным числом, равным данному десятичному числу?
3. Для каких целей используются восьмеричная и шестнадцатеричная системы счисления?
4. Выполните наиболее рациональным способом следующие переводы чисел: 537,158 Ь; 537,158 Х16; 10111011010101,010112 хв У16.
5. Напишите двоично-четверичную таблицу соответствия.
Практикум. Раздел 1 «Системы счисления»
1 .3.5. Арифметика в позиционных системах счисления
Выполнение арифметических вычислений в позиционных системах счисления производится по общим правилам. В их основе лежат таблицы сложения и умножения однозначных чисел.
 |
Сложение производится поразрядно, начиная с младшего разряда. Если при суммировании цифр одного разряда сумма оказывается больше р — 1 (т. е. двузначным числом), то в данном разряде результата записывается младшая цифра суммы, а старшая цифра прибавляется к следующему по старшинству разряду (ближайшему слева).
Вычитание — обратная к сложению операция. Если в очередном разряде уменьшаемого стоит цифра, меньшая чем у вычитаемого, то занимается единица у ближайшего слева ненулевого разряда. В результате к вычисляемому разряду уменьшаемого добавляется р. Если единица занималась не у соседнего слева разряда, то к промежуточным разрядам добавляется р — 1.
Умножение сводится к многократному сложению со сдвигом разрядов, а деление — к многократному вычитанию.
Двоичная арифметика. Вот как выглядят таблица сложения и таблица умножения в двоичной системе счисления:
Таблица сложения Таблица умножения в двоичной системе в двоичной системе
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
10 |
|
|
|
Рассмотрим примеры выполнения четырех арифметических
операций с двоичными числами. Замечание: далее нижний индекс для обозначения
системы счисления будет опускаться.
Пример 1. Сложение двоичных чисел. Маленькими цифрами сверху обозначены значения, переносимые при сложении в соседний слева разряд.
1 1 1 1 1
+ 1 0 1 1 0 0 1 1 1
1 1 0 1 1 0 1 0 0
Пример 2, Вычитание двоичных чисел. Маленькими цифрами сверху обозначены значения, добавляемые к разряду в процессе
переноса единицы из ближайшего ненулевого разряда слева.
-1 1 10
|
|
Теоретические основы информатики |
 |
1 0 1 1 0 0 1 1 1
1 0 0 1 1 0 1
1 0 0 0 1 1 0 1 0
Правильность полученного результата можно проверить путем сложения разности с вычитаемым. В результате должно получиться уменьшаемое.
Пример З. Умножение двоичных чисел.
1 0 1 1 0 1 1
1 1 1 0 0 0 1 1 1
Пример 4, Деление двоичных чисел. В следующем примере делимым числом является произведение из предыдущего примера, делителем второй сомножитель. Частное получилось равным первому сомножителю.
Двоичная арифметика — наиболее простая. Эта простота стала одной из причин использования двоичной системы счисления в компьютере.
Арифметика в других системах счисления. Приведем примеры вычислений в других системах счисления. Рассмотрим пятеричную систему.
|
Таблица сложения |
Примеры сложения и вычитания |
|
в пятеричной системе |
пятеричных чисел: |
|
апоппп |
|||||
|
о |
о |
1 |
2 |
з |
4 |
|
1 |
1 |
2 |
з |
4 |
10 |
|
2 |
2 |
З |
4 |
10 |
11 |
|
з |
з |
4 |
10 |
11 |
12 |
|
4 |
4 |
10 |
11 |
12 |
13 |
-1 10 -1 10
1 [1] -1 10
|
|
49[2] |
|
Системы счисления |
|
2
о З 4 1 о з 1 
2 о З 4
з [3] 2 1
Таблица умножения Примеры умножения и деления
в пятеричной системе пятеричных чисел:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
о |
1 |
|
|
|
|
2 |
о |
2 |
4 |
11 |
13 |
|
з |
о |
з |
11 |
14 |
22 |
|
4 |
о |
4 |
13 |
22 |
31 |
2 1 з
4 2 1 1 3 2
з
2
4 2 1 3
з 2
Задача 1. Вычислить сумму двух шестнадцатеричных чисел: 3A8D,1F16 + 2С6,516.
Используем описанный ВЫШе алгоритм.
Задача 2. В среде электронных таблиц создать автоматически заполняемую таблицу умножения для восьмеричной системы счисления.
|
|
|
|
Теоретические основы информатики |
 |
|
|
А |
|
в |
с |
D |
Е |
|
|
|
|
1 |
|
Таблица умножения |
8 |
-ричной системы |
|
||||
|
2 |
|
|
|
|
|
|
|
|
|
|
з |
|
|
1 |
2 |
з |
4 |
5 |
6 |
7 |
|
4 |
1 |
|
1 |
2 |
з |
4 |
5 |
б |
7 |
|
5 |
2 |
|
2 |
4 |
6 |
10 |
12 |
14 |
16 |
|
|
|
|
|
|
11 |
14 |
17 |
22 |
25 |
|
7 |
4 |
|
4 |
10 |
14 |
20 |
24 |
30 |
34 |
|
8 |
5 |
|
5 |
12 |
17 |
24 |
31 |
36 |
43 |
|
9 |
б |
|
6 |
14 |
22 |
30 |
36 |
44 |
52 |
|
10 |
7 |
|
7 |
16 |
25 |
34 |
43 |
52 |
61 |
Таблица создается в такой последовательности:
1. В ячейку D1 заносится число 8 — основание системы счисления. Поясняющий текст заносится в соседние ячейки первой строки.
2. В блок ВЗ:НЗ заносятся числа от 1 до 7. З. В блок А4:А1О заносятся числа от 1 до 7.
4. В ячейку В4 заносится формула:
5. Формула из ячейки 134 копируется в блок В4:Н1О. Таблица готова!
Здесь используются две стандартные функции электронных таблиц:
ЦЕЛОЕ(число) выделение целой части числа, стоящего в аргументе;
ОСТАТ(число; делитель) остаток целочисленного деления (аналог операции тост в Паскале).
Учимся программировать
(целочисленная арифметика)
Задача 3. Создать программу на Паскале, выводящую на экран таблицу умножения в системе счисления с основанием р (2 10).
Program ТаЬ1 ти1; var Х, У, Z, р: integer; begin
Ввод основания системы}
Write ( ' Введите р (2<р<=1О) :
Read1n (р) ; 
—ичная таблица умножения ' ) ; for Х
:=1 €0 Р—1 do {Изменение первого сомножителя} begin for У :=1 Р—1 do
{Изменение второго сомножителя 
begin Вычисление произведения и перевод в
р—ичную систему}
Z:=(X*Y div р) * 10 + (Х * У) mod р; Write (Z : 3) (вывод произведения без перевода строки) end;
Write1n {перевод строки} епа end.
 |
Введите р 
. 8
8—ичная таблица
умножения
7
14 16
 |
36 43
44 52
52 61
1 2 З 4 5 2 4 6 10 12 З 6 1114 17
4
|
5
12 17 24 31
14 2236
7 16 25 34 43
Вопросы и задания
1. Проверьте для двоичной системы счисления выполнение трех арифметических законов:
а) коммутативности: а + Ь = Ь + а; а • Ь = Ь • а;
б) дистрибутивности: с • (а + Ь) = с • а + с • Ь;
в) ассоциативности: (а + Ь) + с = а + (Ь + с); (а • Ь) • с = а • (Ь • с).
Выполните проверку на
примере значений: а = 1102 Ь = 10112 с = 112
2. Сформулируйте словесно алгоритм сложения многозначных чисел в р-ичной позиционной системе счисления.
3. Постройте таблицы сложения и умножения для троичной системы счисления.
О 4. Используя результат предыдущего задания, выполните вычисления в троичной системе:
О 5. Используя смешанные системы «2—8» и «2—16», выполните вычисления: 73564,3248 + 17654,1238; F19C5,7A16 - 4ТВ,ЗЗС916.
Практикум. Раздел 1 «Системы счисления»
|
|
Теоретические основы информатики |
 |
1 .4.1 . Информация и сигналы
Человек воспринимает информацию из внешнего мира с помощью своих органов чувств. Ббльшая часть информации принимается нами через зрение и слух. Органы слуха воспринимают звуковые сигналы, органы зрения воспринимают световые сигналы,
Сигнал переносит информацию, представленную в виде знао чения или изменения значения физической величины.
Звуковой сигнал связан с изменением давления воздуха, порожденным звуковой волной и воздействующим на орган слуха. Световые сигналы, воспринимаемые нашим зрением, — это электромагнитные волны в определенном диапазоне частот диапазоне видимого света.
Различают два вида сигналов: непрерывные и дискретные. Например, звук это непрерывный волновой процесс, происходящий в атмосфере или другой сплошной среде. Непрерывный электрический сигнал в технических системах передачи и обработки информации называют аналоговым сигналом. Термин «дискретный» означает «разделенный», состоящий из отдельных частиц, элементов. При цифровой передаче и обработке информации используются дискретные сигналы.
Многие века люди могли слышать звуки только на расстоянии естественной слышимости от источника, видеть объекты, находящиеся в поле зрения. Развитие науки и техники позволило человеку выйти за эти естественные границы восприятия.
В течение двух последних столетий ученые и изобретатели достигли больших результатов в создании средств связи для передачи информации на расстояние.
XIX век был веком великих технических изобретений. В 1831 году Майкл Фарадей открывает явление электромагнитной индукции. После этого начинается бурное развитие электротехники: изобретается электрический генератор, создаются средства передачи электроэнергии на расстояние. Электричество находит множество применений. Важнейшие из них: электрическое освещение и отопление, электрический двигатель, электросвязь передача информации с помощью электричества. Идея передачи информации по проводам по тем временам казалась фантастической: появилась возможность передавать текст со скоростью переноса электрического сигнала близкой к скорости света.
|
Кодирование |
 |
Первый электромагнитный телеграф создал российский ученый Павел
Львович Шиллинг в 1832 году. В 1837 году американец Сэмюэл Морзе запатентовал
свою конструкцию электромагнитного телеграфного аппарата. Он же
разработал телеграфный код, известный под названием азбуки Морзе.
Телеграф — это Дискретный способ переДачи информации.
Телеграфное сообщение представляет собой
|
последовательность электрических сигналов |
Сэмюэл Финли |
|
разной длительности, переносимых от одного |
Бриз Морзе |
|
телеграфного аппарата по проводам к друго- |
(1791-1872) |
му телеграфному аппарату. Морзе принадлежит идея использования всего двух видов сигналов — короткого и длинного для кодирования сообщения с целью передачи его по линиям телеграфной связи.
В азбуке Морзе каждая буква алфавита кодируется последовательностью коротких сигналов («точек») и длинных сигналов («тире»). На рисунке 1.7 показана азбука Морзе применительно к латинскому и русскому алфавитам.
Самым знаменитым телеграфным сообщением является сигнал бедствия «SOS» (Save 0ur Souls — спасите наши души). Вот как
|
|
|
|
|
л |
|
с |
ц |
|
|
в |
|
|
м |
м |
|
|
|
|
|
|
в |
|
|
н |
|
|
|
|
|
|
|
|
о |
о |
|
Q |
щ |
|
|
D |
д |
|
Р |
п |
|
|
ъ |
|
|
Е |
Е |
|
|
|
|
|
ы |
|
|
v |
ж |
|
|
с |
|
х |
ь |
|
|
z |
з |
|
т |
т |
|
|
Э |
|
|
|
и |
|
|
|
|
|
ю |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 .7. Кодовая таблица азбуки Морзе
Три точки обозначают латинскую букву «S», три тире — букву «О». Две паузы отделяют буквы друг от друга. Телеграфист, передававший сообщение на азбуке Морзе, «выстукивал» его с помощью телеграфного ключа: «точка» короткий сигнал, «тире» — длинный сигнал, после каждой буквы пауза. На принимающем аппарате сообщение записывалось на бумажной ленте в виде графических точек, тире и пробелов, которые вивуально прочитывал телеграфист.
Азбука Морзе является неравномерным кодом, поскольку у разных букв алфавита длина кода разная — от одного до шести символов (точек и тире). По этой причине необходим третий символ — пауза для отделения букв друг от друга.
|
|
Теоретические основы информатики |
 |
Равномерный телеграфный код был изобретен французом Жаном Морисом
Бодо в 1870 году. В нем использовалось всего два разных вида сигналов. Неважно,
как их назвать: точка и тире, плюс и минус, ноль и единица. Это два
отличающихся друг от друга электрических сигнала.
В кодовой таблице Бодо длина кодов всех символов алфавита одинакова и равна пяти. В таком случае не возникает проблемы от-
|
Жан Морис Эмиль |
деления букв друг от друга: каждая пятерка |
|
Бодо (1845-1903) |
сигналов это знак текста. |
Благодаря идее Бодо, удалось автоматизировать процесс передачи и печать букв. В 1901 году был создан клавишный телеграфный аппарат. Нажатие клавиши с определенной буквой вырабатывает СООТВУГСТвующий пятиимпульсный сигнал, который передается по линии связи. Принимающий аппарат под воздействием этого сигнала печатает ту же букву на бумажной ленте.
Следующим важным событием в технике связи стало изобретение телефона. В 1876 году американец Александр Белл получил патент на его изобретение. Годом позже Томас Э. Эдисон изобрел телефонный аппарат с угольным микрофоном, который можно встретить до сих пор. По телефонной связи на расстояние передается звук посредством непрерывного электрического сигнала, модулированного с частотой звуковых колебаний. В микрофоне говорящего человека создается переменное электрическое напряжение, а в наушнике слушающего оно преобразуется в звуковые колебания.
Телефонная связь это аналоговый способ переДачи звука.
|
|
|
 |
Благодаря открытию в 1888 году Генрихом Герцем электромагнитных волн
стало возможным изобретение радиосвязи. Почти одновременно в 1895 году
Александр Степанович Попов в России и в 1896 году итальянец Гульельмо Маркони
изобрели первые радиопередатчики и радиоприемники. Современники изобретения
называли радио беспроводным телефоном. Принцип передачи звука по радиосвязи
заключается в переносе через пространство высокочастотных
|
(несущих) электромагнитных волн, модули- |
Александр |
|
рованных по амплитуде низкочастотными |
Степанович |
|
звуковыми колебаниями. В радиоприемнике |
|
|
звуковые колебания отделяются от несущей частоты и преобразуются в звук. |
попов (1859-1906) |
Радиосвязь — это аналоговый способ передачи звука.
В ХХ веке с изобретением телевидения стала возможной передача на расстояние изображения. Телевизионный электромагнитный сигнал это также аналоговый способ переДачи звуковой и видеоинформации.
Во второй половине ХХ века происходит переход к преимущественно дискретной форме представления информации для ее хранения, передачи и обработки. Этот процесс начался с изобретением цифровой вычислительной и измерительной техники. В настоящее время компьютерная обработка становится элементом всех систем связи: телефонной, радио- и телевизионной. Развивается цифровая телефония, цифровое телевидение. Интернет как универсальная система связи основан исключительно на дискретной цифровой технологии хранения, передачи и обработки ин-
О Система основных понятий
|
Информация и сигналы |
|||
|
Сигнал переносит информацию, представленную в виде значения или изменения значения физической величины |
|||
|
Аналоговый сигнал — непрерывный |
Дискретный сигнал — состоящий из отдельных (отличимых друг от друга) элементов |
||
|
Аналоговые способы передачи информации |
Дискретные способы передачи информации |
||
|
Технические средства |
Время изобретения |
Технические средства |
Время изобретения |
|
Телефон |
1876 год |
Телеграф Морзе |
1837 год |
|
РаДио |
1895 год |
Телеграф Бодо |
1870 год |
|
ТелевиДение |
1930-е годы |
Цифровые технологии связи: электронная почта, цифровая телефония, цифровое телевиДение, Интернет |
Вторая половина ХХ века |
|
|
Теоретические основы информатики |
 |
1. Что вы понимаете под сигналом?
2. Обоснуйте правильность употребления фразы «сигнал светофора».
3. Приведите примеры непрерывных сигналов в природе, передающих информацию.
4. Как вы считаете, человеческая речь — это непрерывная или дискретная форма передачи информации?
5.
Перечислите
основные события в истории изобретения технических средств связи. Подготовьте
презентацию.
6. Почему в последнее время цифровые технологии связи вытесняют аналоговые? Подготовьте доклад.
1 .4.2. Кодирование текстовой информации
Что такое кодирование
Чтобы информацию можно было хранить, передавать и обрабатывать, ее нужно представить в удобной для этого форме.
Кодирование — это
процесс представления информации в виде последовательности условных
обозначений. Кодом называют множество слов последовательностей символов из
некоторого алфавита, используемых при кодировании информации.
Кодирование происходит по определенным правилам. Правила кодирования зависят от назначения кода, т. е. от того, как и для чего он будет использоваться.
Письменность это способ кодирования устной речи на естественном языке. Письменный текст предназначен для передачи информации от одного человека к другим людям как в пространстве (письмо, записка), так и во времени (книги, дневники, архивы документов и пр.). Правила, по которым люди осуществляют письменное кодирование информации, называются грамматикой языка (русского, английского, китайского и др.), а человека, умеющего читать и писать, называют грамотным человеком.
Запись речи кодирование, а чтение письменного текста
это
его декодирование. Процесс письменного обмена информацией между людьми можно
отобразить следующей схемой:
|
Кодирование |
|
 |
Процесс передачи телеграфного сообщения с использованием азбуки Морзе можно отразить следующей схемой:
Кодирование текста всегда происходит по следующему
правилу: каждый символ алфавита исходного текста заменяется на комбинацию
символов алфавита кодирования. Для азбуки Морзе эти правила представлены на
рис. 1.7.
В таблице азбуки Морзе для кодирования 32 букв русского
алфавита (буква «Ё» стала использоваться в письменном тексте только в середине
ХХ века) применяются два символа: точка и тире. Однако при передаче слов из-за
неравномерности коДов различных букв приходится применять еще пропуск между
буквами: паузу во времени передачи или пробел на телеграфной ленте. Поэтому
фактически алфавит телеграфного кода Морзе содержит три символа: точка, тире,
пропуск. Это троичный код.
Телеграфный код Бодо является двоичным равномерным пятиразряДным кодом. На его основе в 1932 году был разработан международный телеграфный код ITA2, кодовая таблица которого представлена на рис. 1.8.
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ев |
29 |
|
ев |
ас |
|
|
ГЕ |
ан |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
11 19 |
12
|
13 пыаащ»шашанцетод |
14 |
15 1) |
16 |
17 |
||||||||
|
|
1F |
||||||||||||||
|
|
18 |
|
|
|
|
1B |
|
1C |
|
|
|
1Е |
|
||
|
Let1ers |
Fi ures |
Control Chars. |
|||||||||||||
|
|
Тео етические основы ин о матики |
 |
Двоичные коды
символов свернуты в формат двузначных шестнадцатеричных чисел, в которых первая
цифра это О или 1. Есть три типа символов: буквы (letters), цифры и знаки
(figures), управляющие символы (control chars). Переключение в режим ввода букв
происходит по коду 1F16 (двоичная форма
ОА16 (О 1010). Этот же код в режиме ввода цифр обозначает цифру 4. Слово BODO в шестнадцатеричной форме кодируется так: 19 18 09 18. Длина двоичного кода этого слова равна 20.
Во второй половине ХХ века создаются и распространяются компьютеры. Для компьютерной обработки текстов потребовалось создать стандарт кодирования символов. В 1963 году был принят стандарт, который получил название ASCII — Американский стандартный код для информационного обмена. ASCII семиразрядный двоичный код, представлен в табл. 1.4.
Код символа — это его порядковый номер в кодовой таблице, определяется номером строки и столбца. Он может быть представлен в десятичной, в двоичной и в шестнадцатеричной системах счисления. Код в памяти компьютера семиразрядное двоич-
Таблица 1.4 Кодировка ASCll
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О. |
МЛ, |
SOH |
STX |
ЕТХ |
гОТ |
ENQ |
АСК |
BEL |
BS |
ТАВ |
|
VT |
FF |
CR |
SO |
SI |
|
1. |
ЛЕ |
DC1 |
DC2 |
DC3 |
DC4 |
NAk |
SYN |
ЕТВ |
САН |
ЕМ |
stJB |
ESC |
FS |
GS |
RS |
US |
|
2. |
про— бел |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
с |
D |
Е |
|
|
н |
|
|
к |
1, |
м |
|
о |
|
|
|
|
|
|
|
|
|
|
х |
У |
z |
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
Ј |
К |
1 |
т |
п |
|
|
|
|
q |
r |
|
|
|
|
w |
х |
|
|
|
|
|
|
DEL |
ное число. В таблице 1.4 код ASCII
представлен в свернутой шестнадцатеричной форме. При развертывании в двоичную
форму коды представляют собой семиразрядные целые двоичные числа в диапазоне от
ООО 00002 0016 
7F16 127. Всего с помощью этого кода
представляются 2 7 = 128 символов.
|
|
59 |
|
Кодирование |
|
Первые 32 символа (от 00 до 1F) называются
управляющими символами. Они не отражаются какими-либо знаками на экране
монитора или при печати, но определяют некоторые действия при выводе текста.
Например, по коду 0816 (BS) происходит стирание предыдущего символа; по коду
0716 (ВЕГА) вывод звукового сигнала; код ()D16 (CR) означает переход к началу
строки (возврат каретки). Эти символы унаследованы еще от кодировки для
телетайпной связи, для которой первоначально использовался код ASCII, поэтому
сохранились такие архаичные термины, как «каретка
Символы, имеющие графическое отображение, начинаются с кода 2016. Код 2016 это код пробела: пропуска позиции при выводе. Важным свойством таблицы ASCII является соблюдение алфавитной последовательности кодировки прописных и строчных букв, а также десятичных цифр. Это свойство чрезвычайно важно для программной обработки символьной информации, в частности для алфавитной сортировки слов.
Расширение кода ASCII. Восьмиразрядная двоичная кодировка позволяет кодировать алфавит из 28 — 256 символов. Первая половина восьмиразрядного кода совпадает с ASCII. Вторая половина состоит из символов с кодами от 128 = 8016 1000 00002 до 255 = FF16 вается кодовой страницей (СР — code page). На кодовой странице размещают нелатинские алфавиты, символы псевдографики и некоторые другие знаки, не входящие в первую половину.
В таблицах 1.5—1.7 приведены кодовые страницы с русским алфавитом. СР866 используется в операционной системе MS DOS, СР1251 — в операционной системе Windows. Кодировка k018-R используется в операционной системе Unix. Таблица 1.5
|
|
Теоретические основы информатики |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хаввгдваашивашш•ш |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.6
Кодовая страница СР 1251
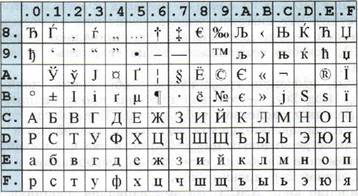
Обратите внимание на то, что не во всех кодировках соблюдается правило последовательного кодирования русского алфавита.
Существуют и другие стандарты символьной кодировки, где присутствует русский алфавит.
Таблица 1.7 k018-R
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е. |
П Я Р С Т У Ж В Ь Ы З Ш ЭЩ Ч Ъ |
|||||||||||||||
|
Кодирование |
|
 |
В начале кодовой таблицы — в области от 000016 до
007F16 содержатся символы ASCII. Под символы кириллицы выделены области знаков
с кодами от 040016 до 052F16, от 2DE016 до 2DFF16, от Аб4О16 до A69F16
Позднее стали разрабатываться новые стандарты на Unicode. К 2010 году сменилось 6 вариантов стандарта. Благодаря более сложной организации кода, при сохранении его 16-разрядности появилась возможность кодировать 1 112 064 символа. В настоящее время из этого количества реально используется около 107 тысяч кодов.
Учимся программировать
(обработка символьной информации)
Рассмотрим программу на Паскале, по которой на экран будет выводиться таблица кодировки в диапазоне кодов от 20 до 255.
Program ТаЬ1 code ;
Uses
CRT ; (Подключение библиотеки управления символьным выводом) Var kod: byte;
(Целые числа от О до 255} begin c1rscr; (Очистка экрана символьного вывода 
for
kod €0 255 do (Перебор кодов символов) begin
{ Перевод строки через 10 шагов}
if (kod mod 10 — О) then Write1n; 
Write (chr (kod) : З, kod:4) ; (Вывод символа и его кода} end
|
|
Теоретические основы информатики |
 |
Переменная типа byte занимает 1 байт памяти и принимает множество целых положительных числовых значений в диапазоне от о до 255.
В программе используется стандартная функция chr (kod) , которая в качестве результата возвращает символ, десятичный код которого равен значению переменной kod.
Значения выводятся парами: символ — код. В одной строке располагается 10 таких пар. Вся таблица разместится в 24 строках.
О Система основных понятий
|
Кодирование текста |
||||||
|
Кодирование — процесс представления информации в виде последовательных словных обозначений |
||||||
|
Преобразование устного сообения в письменн м |
Перевод из одной знаковой системы в ю |
|||||
|
Декодирование — преобразование, обратное кодированию |
||||||
|
Телег а ные ко |
омпьюте ные и |
вые ко |
||||
|
Код Мо зе |
код Бо о |
Стандарт ITA2 |
ASCII |
Кодовые с ани ы |
Unicode |
|
|
Неравномерный троичный код |
Равномерный пятиразрядный двоичный код |
7-разрядный двоичный код |
8-разрядное расширение ASCII, включающее национальные ал авиты |
16-разрядный международный код |
||
1.
Определите
понятия: код, кодирование, декодирование.
2.
Приведите примеры
кодирования и декодирования, о которых не говорилось в параграфе.
З. В чем разница между равномерным и неравномерным кодами?
4. Закодируйте слово COMPUTER, используя коды ITA2 и ASCII.
5. Как прочитается фраза ШАЙБУ-ШАЙБУ!, закодированная с использованием СР1251, если декодирование происходит по коду k018-R?
6. В кодировке k018-R было составлено письмо, начинающееся фразой «Здравствуй, дорогой Саша!». Декодирование происходило по семиразрядному коду ASCII, в результате чего старший (восьмой) бит у всех символов был утерян. Напишите, какой текст получился в итоге. Сможет ли адресат понять содержание письма?
Практикум. Раздел 2 «Кодирование»
1.4.3. Кодирование изображения
 |
С древних времен люди научились сохранять и передавать изображения в форме рисунков. В XIX веке появилась фотография. Изобретение кино братьями Люмьер в 1895 году позволило передавать движущиеся изображения. В ХХ веке изобретают видеомагнитофон — средство записи и передачи изображения на магнитной ленте.
Приемы кодирования изображения разрабатываются с появлением цифровых технологий хранения, передачи и обработки изображений: цифровой фотографии, цифрового видео, компьютерной графики.
При кодировании изображения в компьютерных технологиях осуществляется пространственная Дискретизация изображения и коДирование света, исходящего от кажДого Дискретного элемента изображения. Дискретизация изображения — это разделение изображения на конечное число элементов, в пределах каждого элемента оттенок цвета считают постоянным. Пространственная сетка дискретных элементов, из которых строится изображение на экране монитора, называется растром. Сами дискретные элементы изображения на экране называются пикселями (рис. 1.9). Чем гуще сетка пикселей, тем выше качество изображения, тем
Рис. 1-9. Увеличенное растровое изображение
меньше наши глаза замечают его дискретную структуру.
Код изображения, выводимого на экран, это последовательность двоичных кодов света, излучаемого всеми пикселями растра.
 |
цветная
фотография и цветное кино. То же самое относится к телевидению. Первые
компьютерные дисплеи отображали «чернобелое» изоражение, а современные мониторы
— цветное.
Кодирование монохромных оттенков
Слово «монохромный» означает
«одноцветный». Имеется один фоновый цвет. Все изображение получается с помощью
оттенков этого фонового цвета, различающихся яркостью. Например, если фоновый
цвет черный, то путем его постепенного осветления можно перейти через оттенки
серого к белому цвету (рис. 1.10). Такое непрерывное множество оттенков от
черного до белого назовем черно-белым спектром. Из таких оттенков и получается
изображение на черно-белой фотографии, на кино- и телеэкране.
Однако фоновый цвет не обязательно должен быть черным. Он может быть коричневым, синим, зеленым и др. Такое бывает на тонированных фотографиях. Существовали монохромные мониторы с коричневым или зеленым фоновым цветом.
Рис. 1.10. Непрерывный чёрно-белый спектр
Код монохромного света обозначает уровень яркости фонового цвета. Для цифрового кодирования цвета в компьютере используются положительные целые двоичные числа. Длина двоичного кода в битах называется битовой глубиной кодирования цвета.
При дискретном цифровом кодировании непрерывный спектр оттенков фонового цвета разбивается на целое число отрезков, в пределах каждого из которых яркость считается постоянной. Это называется дискретизацией спектра.
Для естественного света количество оттенков фонового цвета бесконечно. При цифровом кодировании количество оттенков становится конечной величиной.
Количество оттенков К и битовая глубина кодирования Ь 
связаны
между собой по формуле:
Снова работает главная формула информатики!
|
|
65 |
 |
На рисунке 1.11 показана дискретизация черно-белого спектра при Ь 2. Это значит, что длина кода равна 2 битам и весь спектр разбивается на четыре уровня — 4 оттенка.
|
Спектр: |
|
|
|
|
|
Яркость: |
о- 1/4 |
1/4 - 2/4 |
2/4 - 3/4 |
3/4- 1 |
|
Код десятичный: |
|
1 |
2 |
з |
|
Код двоичный: |
оо |
01 |
10 |
11 |
Рис. 1 .11. Монохромное кодирование с битовой глубиной
цвета 2
Естественный свет, яркость которого лежит в диапазоне от О до 1/4, будет представляться как черный цвет, десятичный код которого О, а двоичный код — 00. Далее идут два серых оттенка. Свет в диапазоне яркости от 3/4 до 1 представляется как
белый, его код: З = 112. Если уровень яркости выражать в процентах, то правила черно-белого кодирования при Ь = 2 можно отразить в таблице:
|
ет |
Яркость |
Десятичный код |
Двоичный код |
|
Черный |
0-250/0 |
|
оо |
|
Темно-серый |
25—50 % |
1 |
01 |
|
Светло-серый |
50—75 % |
2 |
10 |
|
Белый |
75-1000,6 |
з |
11 |
На рисунке 1.12 показана дискретизация черно-белого спектра при Ь = 4. Поскольку 24 = 16, таким способом кодируются 16 различных черно-белых оттенков. Приведены десятичные и двоичные коды.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
1 |
2 |
з |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 .12. Монохромное кодирование с битовой глубиной цвета 4
 |
На экране нарисована буква «П». Три
составляющих ее отрезка окрашены в разные оттенки фонового цвета: черный,
темно-серый и светло-серый. Двоичный код изображения показан справа.
11 11 11 11 11 11 11 11
11 01 01 01 01 01 11 11
11 00 11 11 11 10 11 11
11 оо 11 11 11 10 11 11
11 00 11 11 11 10 11 11
11 оо 11 11 11 10 11 11
11 11 11 11 11 11 11 11
11 11 11 11 11 11 11 11
Рис. 1.13. Дискретный рисунок и его код
Для наглядности двоичный код представлен в виде матрицы, строки которой соответствуют строкам растра на экране. На самом же деле память компьютера одномерна и весь код представляет собой цепочку нулей и единиц, расположенных в последовательных байтах памяти. Объем такой информации равен 16 байтам. Если перевести этот код в шестнадцатеричную форму, то он будет следующим:
FFFF D55F CFEF CFEF CFEF CFEF FFFF FFFF
При кодировании цветного изображения используются различные подходы, которые называются моделями цвета. Об этом подробно будет рассказано в разделе, посвященном технологиям компьютерной графики.
 |
|
Ко ование изоб ажения |
|||
|
Изображение — образ внешнего мира, воспринимаемый зрительной системой человека |
|||
|
Человек видит изображение благодаря восприятию света, отражаемого или изл аемого объектами наблю ения |
|||
|
Дискретизация изображения — разделение изображения на конечное число элементов, в пределах каждого элемента оттенок цвета считают постоянным |
|||
|
|
Монохромное изображение: |
Фоновый вет — основной цвет изоб ажения |
|
|
Оттенки отличаются яркостью фонового цвета. Белый вет имеет максимальнуццркость Битовая глубина цвета (Ь) — длина двоичного ко а вета |
|||
|
К = 2 6 — количество оттенков вета |
|||
|
Код изображения: последовательная цепочка ко ов всех иск етных элементов изоб ажения |
|||
|
Цветное изоб ажение: |
Код зависит от используемой моДели цвета |
||
Вопросы и задания
1.
Дайте определения
понятий: свет; цвет; изображение.
2. Чего нельзя увидеть и что можно увидеть в абсолютной темноте?
З. Что такое растр, пиксель?
4. Чем отличается монохромное изображение от цветного?
5. Что представляет собой черно-белый спектр?
6. Какая информация заключается в компьютерном коде изображения?
|
О |
7. Какую длину будет иметь код изображения, выводимого на экран, при размере растра 640 х 480 и битовой глубине цвета 8 битов? |
|
О |
8. Какова глубина кодирования изображения, если длина кода равна 384 Кб, а размер растра — 1024 х 768? |
|
О |
9. Длина кода изображения равна 600 Кб, битовая глубина цвета — 16 битов. Какой размер растра используется для вывода изображения: 640 х 480 или 1024 х 768? 10. На «игрушечный» монитор с разрешением 8 х 8 пикселей, отображающий черно-белое изображение (см. пример в параграфе), по очереди выводятся буквы: «Н», «А», «Ш». Запишите для каждого выводимого изображения его двоичный и шестнадцатеричный коды. Битовая глубина цвета равна 2. Разные элементы букв имеют разные цвето- |
вые оттенки.
11. Восстановите изображение на
«игрушечном» мониторе из задания 10 по шестнадцатеричному коду: F3F7 F3D7 F37F
F1FF F3BF F3EF F3FB FFFF, если битовая глубина цвета равна 2. 
1 .4.4. Кодирование звука
Технология кодирования непрерывного сигнала
В параграфе 1.4.1 было разъяснено, что такое непрерывный сигнал и дискретный сигнал. Свет переносится непрерывным потоком электромагнитного излучения. Звук переносится акустической волной, порождающей непрерывный процесс изменения давления воздуха со звуковой частотой. Поэтому световые и звуковые сигналы являются естественными (существующими в природе) непрерывными сигналами.
 |
Рис. 1 .14. Преобразование непрерывного сигнала в цифровой код
Из данной схемы следует, что как световой, так и звуковой сигнал первоначально преобразуется в непрерывный (аналоговый) электрический сигнал. Процесс преобразования непрерывного
электрического сигнала в дискретную цифровую форму называется аналого-цифровым преобразованием, или сокращенно АЦП.
Оцифровка изображения происходит во время съемки на
цифровые фото- и видеокамеры, а также при вводе изображения в компьютер с
помощью сканера. В основе физического процесса преобразования света в
электрический ток лежит явление возникновения электрического заряда в
полупроводниковом приборе 
фотодиоде под действием падающего на него
света.
Величина возникающего на фотодиоде электрического потенциала пропорциональна яркости светового потока. Эта величина изменяется непрерывно вместе с изменением яркости света.
Аналого-цифровое преобразование заключается в измерениях величины электрического сигнала через определенные промежутки времени и сохранении результатов измерений в цифровом формате в устройстве памяти.
|
Кодирование |
|
 |
Аналого-цифровое преобразование звука
Рассмотрим подробнее процесс АЦП на примере кодирования звука при его вводе в компьютер. При записи звука в компьютер устройством, преобразующим звуковые волны в электрический сигнал, является микрофон. Аналого-цифровое преобразование производит электронная схема, размещенная на звуковой плате (звуковой карте) компьютера, к которой подключается микрофон.
Амплитуда и частота исходящего от микрофона и поступающего на звуковую плату электрического сигнала соответствует амплитудным и частотным характеристикам акустического сигнала. Поэтому измерение электрического сигнала (силы тока в цепи) позволяет определить характеристики звуковой волны: ее частоту и амплитуду.
Есть два основных параметра кодирования звука: частота дискретизации и битовая глубина кодирования. Измерение амплитуды сигнала производится через одинаковые промежутки времени (рис. 1.15). Величина такого временнбго интервала называется шагом дискретизации, он измеряется в секундах. Обозначим шаг дискретизации т (с). Тогда частота дискретизации выразится формулой:
Н = 1/т (Гц).
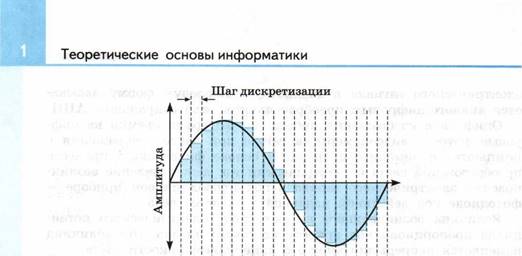
Время, отсчёты
Рис. 1 .15. Дискретизация аналогового сигнала
Частота измеряется в герцах. Один герц соответствует
одному измерению в секунду: 1
Чем выше частота дискретизации, тем более подробно числовой код будет отражать изменение амплитуды сигнала со временем. Хорошее качество записи звука получается при частотах дискретизации 44,1 кГц и выше (1 кГц = 1000 Гц).
Процесс дискретизации амплитуды звука называют квантованием звука. Количество уровней разбиения амплитуды сигнала можно назвать количеством уровней квантования звука (рис. 1.16).
 |
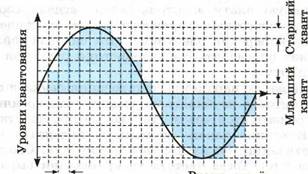
Время, отсчёты
Шаг дискретизации
Рис. 1.16. Квантование аналогового сигнала
Битовая глубина кодирования звука Ь связана с количеством уровней квантования звука К по формуле:
Значения измеряемой величины заносятся в регистр звуковой карты — специальную ячейку памяти этого устройства. Разрядность регистра равна Ь — битовой глубине кодирования. Далее эту величину будем также называть разрядностью квантования. Результат измерения представляется в регистре в виде целого двоичного числа.
Измеряемая физическая величина округляется до ближайшего к ней целого значения, которое может храниться в регистре звуковой карты.
 |
 |
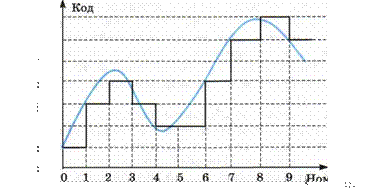
Рис. 1 .17. Измерения переменной физической величины с использованием трёхразрядного регистра
В память компьютера результаты такого измерения будут записаны в виде последовательности трехразрядных двоичных чисел:
|
измерения |
О |
1 |
2 |
з |
4 |
5 |
6 |
7 |
|
|
|
Код |
001 |
011 |
100 |
100 |
010 |
010 |
100 |
110 |
111 |
110 |
Объем записанной звуковой информации равен: З • 10 = 30 битов.
На самом деле трехразрядная дискретизация не используется на практике. Такой вариант рассмотрен здесь лишь в качестве учебного примера. Наименьший размер регистра у реальных звуковых карт 8 разрядов. В таком случае одно измеренное значение займет 1 байт памяти компьютера, а число уровней квантования будет равно 2 8 = 256. Измерения с таким регистром будут в 32 раза более точными, чем при трехразрядном регистре. При 16-разрядном регистре каждая величина в памяти займет 2 байта, а число уровней квантования: 2 16 = 32 768. Чем выше разрядность квантования, тем выше точность измерений физической величины. Но при этом растет и объем занимаемой памяти.
Дискретное цифровое представление аналогового сигнала тем точнее его отражает, чем выше частота дискретизации и разрядность квантования.
|
|
Теоретические основы информатики |
 |
Можно привести следующую образную аналогию этой
теоремы. От размера ячейки рыболовной сети зависит размер рыб, которые будут в
ней удерживаться. Чем меньше ячейки, тем более мелкая рыба удерживается сетью.
Перефразированная на рыбацкий лад теорема Найквиста—Котельникова будет звучать
так: длина стороны квадратной ячейки сети должна быть в два раза меньше 
поперечного
размера самой мелкой рыбы, которую требуется поймать сетями. Например, если
поперечный размер рыбы должен быть не меньше 10 см, то сторона квадратной
ячейки рыболовной сети должна быть не больше 5 см.
О Задача 1. В течение 10 секунд производилась запись звука в компьютер. Определить объем записанной информации, если частота дискретизации была равна 10 кГц, а разрядность квантования 16 битов.
Решение. Количество произведенных измерений звукового
сигнала при частоте дискретизации Н (Гц) за время t (с) вычисляется по формуле:
лт = Н • t. Подставляя данные задачи, получим: „'V = 10 ООО • 10 = 100 ООО
измерений. Разрядность квантования: 16 битов = 2 байта. Отсюда объем звуковой
информации: 
= 100000 • 2 = 200000 байтов =
200000/1024 Кб = 195,3125 Кб.
Задача 2, В файле хранится записанный звук. Данные не подвергались сжатию. Объем файла равен 1 Мб. Известно, что запись производилась с частотой 22 кГц при разрядности квантования звука 8 битов. Определить время звучания при воспроизведении звука, хранящегося в файле.
|
Кодирование |
|
 |
Если воспроизведение записанного звука происходит без
искажения, то время воспроизведения равно времени записи. Отсюда искомая
величина вычисляется по формуле:
При вычислении переведем значения I и Ь в байты, а значение Н — в герцы:
t = 
47,66 с. 
Система основных понятий
|
Кодирование звука |
|
|
Микрофон преобразует звуковые волны в аналоговый электрический сигнал |
|
|
Аналого-цифровое преобразование (АЦП): |
преобразование аналогового сигнала в дискрет ную цифровую форму |
|
Этапы цифрового кодирования света и звука: |
1) преобразование в аналоговый электрически сигнал; 2) дискретизация и измерение; З) занесение в память |
|
Параметры АЦП: |
Н (Гц) — частота дискретизации; Ь (битов) — разрядность квантования; К 2b — количество уровней квантования |
|
Длина цифрового кода: |
I = Н • t • Ь, где t (с) — время записи звука |
|
Теорема Найквиста— Котельникова: |
При оцифровке периодического аналогового сигнала частота дискретизации АЦП должна быть не менее чем в 2 раза выше частоты сигнала |
Вопросы и задания
1. Назовите основные этапы технологии кодирования непрерывного сигнала естественного происхождения.
2. В каких устройствах происходит кодирование света?
З. Какие технические устройства используются для кодирования звука?
4.
Дайте определения
понятий: частота дискретизации; разрядность 
квантования; уровни квантования.
5. Определите длину цифрового кода при записи звука в течение 1 мио нуты, если частота дискретизации равна 44,1 Гц, а разрядность квантования — 8 битов.
6.
Определите
частоту дискретизации при кодировании звука, если О объем звукового файла
оказался равным 500 Кб, время записи 
0,5 минуты, разрядность квантования
16 битов. Файл получен после 500/0 -го сжатия исходного кода.
о 7. Две минуты записи цифрового аудиофайла занимают на диске 5,05 Мб. Частота дискретизации 22 050 Гц. Какова разрядность
квантования?
 |
О 1 .4.5. Сжатие двоичного кода
Любая информация в компьютере представляется в форме двоичного кода. Чем больше длина этого кода, тем больше места в памяти он занимает, тем больше времени требуется для его передачи по каналам связи. Все это сказывается на производительности компьютера, на эффективности использования компьютерных сетей.
Для сокращения объема данных выполняется их сжатие. Сжатие данных — это процесс, обеспечивающий уменьшение объема данных за счет изменения способа их организации. Возможны
две ситуации при сжатии:
1) потеря информации в результате сжатия недопустима;
2) допустима частичная потеря информации в результате сжа-
тия.
При упаковке данных в файловые архивы производится их сжатие без потери информации. Файловые архивы создаются для врёменного хранения на носителях или передачи по каналам связи. Для работы с этими данными требуется их распаковка (разархивирование), т. е. приведение к первоначальному виду. При этом ни один бит не должен быть потерян. Например, если сжатию подвергается текст, то после распаковки в нем не должен быть искажен ни один символ. Сжатая программа также должна полностью восстанавливаться, поскольку малейшее искажение приведет ее в неработоспособное состояние.
Сжатие без потери информации включено также в некоторые форматы графических файлов.
Сжатие с частичной потерей информации производится при сжатии кода изображения (графики, видео) и звука. Такая возможность связана с субъективными возможностями человеческого зрения и слуха.
Исследования ученых показали, что на наше зрение более существенное воздействие оказывает яркость точки изображения (пикселя), нежели ее цветовые свойства. Поэтому объем кода можно сократить за счет того, что коды цвета хранить не для каждого пикселя, а через один, два и т. д. пикселей растра. Чем больше такие пропуски, тем больше сжимаются данные, но при этом ухудшается качество изображения.
При кодировании видеофильмов — динамичного изображения учитывается свойство инерционности зрения. Быстро меняющиеся фрагменты фильма можно кодировать менее подробно, чем статические кадры.
 |
Различные алгоритмы сжатия кодов изображения и звука используются для реализации различных форматов преДставления графики, виДео и звука.
Сжатие без потери информации. Существуют два подхода к решению проблемы сжатия информации без ее потери. В основе первого подхода лежит использование неравномерного кода. Второй подход основан на идее выявления повторяющихся фрагментов кода.
Рассмотрим способ реализации первого подхода. В восьмиразрядной таблице символьной кодировки (например, ASCII) каждый символ кодируется восемью битами и, следовательно, занимает в памяти 1 байт. В параграфе 1.2.3 нашего учебника рассказывалось о том, что частота встречаемости разных букв (знаков) в тексте разная. Там же было показано, что информационный вес символа тем больше, чем меньше его частота встречаемости. С этим обстоятельством и связана идея сжатия текста в компьютерной памяти: отказаться от одинаковой длины кодов символов. Символы с меньшим информационным весом, т. е. часто встречающиеся, кодировать более коротким кодом по сравнению с реже встречающимися символами. При таком подходе можно существенно сократить объем общего кода текста и, соответственно, места, занимаемого им в памяти компьютера.
Мы уже рассматривали азбуку Морзе, в которой применен принцип неравномерного коДа. Если точку кодировать нулем, а тире единицей, то это будет двоичный код. Но возникает проблема отделения букв друг от друга. В телеграфном сообщении она решается с помощью паузы, фактически третьего знака в азбуке Морзе.
Одним из простейших, но весьма эффективных способов построения двоичного неравномерного кода, не требующего специального разделителя, является алгоритм Дэвида Хаффмана. Вариант кодовой таблицы Хаффмана применительно к прописным буквам латинского алфавита приведен в табл. 1.8.
Таблица 1.8
|
|
Теоретические основы информатики |
Вариант кодовой таблицы Хаффмана
|
Буква |
Код Хаффмана |
Буква |
Код Хаффмана |
|
|
100 |
м |
00011 |
|
т |
001 |
|
00010 |
|
|
|
|
00001 |
|
о |
1110 |
|
00000 |
|
|
1100 |
|
110101 |
|
|
1011 |
|
011101 |
|
|
1010 |
в |
011100 |
|
|
0110 |
|
1101001 |
|
н |
0101 |
к |
110100011 |
|
|
11011 |
х |
110100001 |
|
|
|
|
110100000 |
|
|
01001 |
Q |
1101000101 |
|
с |
01000 |
|
1101000100 |
В этой таблице буквы расположены в порядке убывания частоты повторяемости в тексте. Самые часто используемые в текстах буквы «Е» и «Т» имеют коды размером З бита, а самые редкие буквы «Q» и «Ь 10 битов. Чем больше размер текста, закодированного таким кодом, тем меньше его информационный объем по сравнению с объемом при использовании однобайтовой
кодировки.
Особенностью данного кода является его префиксная структура. Это значит, что код любого символа не совпадает с началом кода всех остальных символов. Например, код буквы «Е» — 100. Проанализируйте таблицу 1.8. Там нет ни одного другого кода, начинающегося с этих трех символов. По этому признаку символы отделяются друг от друга алгоритмическим путем.
Пример 1. Используя код Хаффмана, закодировать следующий текст, состоящий из 29 знаков:
WENEEDMORESNOWFORBETTERSKIING
Используя таблицу 1.8, закодируем строку:
|
|
77 |
|
Кодирование |
|
011101 100 1100 100 100 11011 00011 1110 1011 100 0110 1100 1110 011101 01001 1110 1011 011100 100 001 001 100 1011 0110 110100011 1010 1010 1100 00001
После размещения этого кода в памяти побайтно он примет вид:
11100111 01010011 11010110 11100100 00100110 01011011
01101000 11101010 10110000 001
В шестнадцатеричной форме он запишется так:
76 64 9В 1F 5С 6С Е7 53 06 Е4 26 5В 68 ЕА ВО 20.
Таким образом, текст, занимающий в кодировке ASCII
29 байтов, в кодировке Хаффмана займет 16 байтов.
Коэффициентом сжатия называют отношение длины коДа в байтах после сжатия к его Длине до сжатия (т. е. в 8-битовой кодировке). В данном примере коэффициент сжатия оказался равным 16/29 0,55.
Раскодирование (распаковка) текста производится с помощью двоичного Дерева коДирования Хаффмана.
Деревом называется графическое представление (граф) структуры связей между элементами некоторой системы. Дерево состоит из вершин и линий связи. Если линия связи имеет направление и изображается стрелкой, то она называется дугой. В дереве нет циклов. Между любыми двумя вершинами дерева существует единственный путь их соединения по линиям связи. В вершину дерева может входить только одна дуга от «родительской» вершины; из вершины может выходить множество дуг к вершинам-потомкам. Двоичным деревом называется дерево, в котором любая вершина имеет не более двух потомков. Корнем дерева называется единственная вершина, не имеющая родительской вершины. Листьями дерева называются вершины, не имеющие потомков.
|
|
Теоретические основы информатики |
Графическое изображение дерева Хаффмана, соответствующего табл. 1.8, представлено на рис. 1.18.
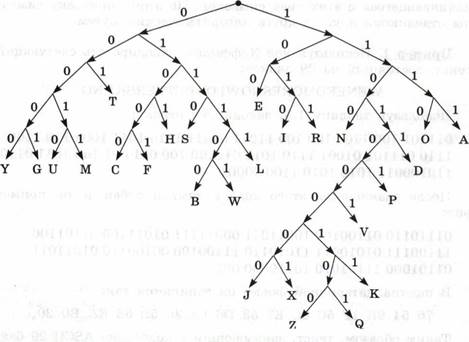
Рис. 1 .18. Двоичное дерево алфавита английского языка, используемое для кодирования по алгоритму Хаффмана
Листьями этого дерева, расположенными на концах ветвей, являются символы алфавита. Код символа формируется из последовательности двоичных цифр, расположенных на пути от корня дерева до листа-символа.
Дерево на рис. 1.18 представляет сокращенный вариант кода Хаффмана. В полном объеме в нем должны быть учтены все возможные символы, встречающиеся в тексте: пробелы, знаки препинания, скобки и др.
|
|
|
7.
Распаковка текста происходит путем сканирования двоичного кода слева направо, начиная с первого разряда, продвигаясь от корня по имеющим данный двоичный код ветвям дерева до тех пор, пока не будет достигнута буква. После выделения в коде буквы процесс раскодирования следующей буквы начинается снова от корня двоичного дерева.
Пример 2, Раскодировать следующий двоичный код, полученный по алгоритму Хаффмана (пробелами код разделен на байты):
Двигаясь по дереву Хаффмана, начиная от первого слева разряда, получим следующую расшифровку:
0101 Н; 00010->U; 01001 ->F; 01001 Р;
Получилось слово HUFFMAN. Упакованный код занимал 4 байта, исходный код 7 байтов. Следовательно, коэффициент сжатия был равен 4/7 0,57.
 |
К методам сжатия путем учета числа повторений фрагментов кода относятся алгоритм RLE и алгоритмы Лемпеля—Зива. В алгоритме RLE выявляются группы идущих подряд одинаковых однобайтовых кодов. Каждая такая группа заменяется на два байта: в первом указывается число повторений (не более 127), во втором — повторяющийся байт. Такой алгоритм благодаря своей простоте работает достаточно быстро. Наибольшую эффективность он дает при сжатии графической информации, содержащей большие области равномерной закраски.
В алгоритмах Лемпеля—Зива (LZ77, LZ78) выявляются повторяющиеся последовательности байтов. Их условно можно назвать словами. Если при последовательном просмотре данных обнаруживается слово, которое уже встречалось раньше, то на него формируется ссылка в виде смещения назад относительно текущей позиции и длины слова в байтах. Программная реализация таких алгоритмов сложнее, чем для метода RLE. Но зато эффект сжатия получается значительно выше».
1) Подробнее об алгоритмах сжатия см. Андреева Е. В.,
Босова Л. Л., Фалина И. Н. Математические основы информатики. Элективный курс. 
БИНОМ. Лаборатория знаний, 2007.
|
|
Теоретические основы информатики |
 |
|
Сжатие двоичного кода |
|||
|
Сжатие — процесс сокращения объема данных путем уменьшения их избыточности |
|||
|
Без потери информации |
С частичной потерей информации |
||
|
Использование неравномерного кодирования: |
код Хаффмана — префиксный код, Двоичное Дерево коДцрования
|
Сжатие кода изображения: |
код цвета пропускается Для части точек растра |
|
Учет повторений фрагментов кода: |
алгоритм RLE: коэффициент повторения + повторяющийся байт; алгоритмы Лемпеля— Зива: словарь повторяющихся слов, ссылки на слова |
Сжатие кода звука: |
уДаление неслышиМЫХ гармоник; использование нелинейной зависимости громкости от амплитуДы |
Вопросы и задания
1. В каких случаях при сэкатии данных можно допускать частичную потерю информации, а в каких нельзя?
2. За счет чего коды переменной длины позволяют сжимать текст?
3. Закодируйте с помощью кодов Хаффмана следующий текст: HAPPYNE\VYEAR. Вычислите коэффициент сжатия.
4. Расшифруйте с помощью двоичного дерева Хаффмана следующий код:
5. В чем идея алгоритма сжатия RLE? Какой тип информации сжимается наилучшим образом по этому алгоритму?
б. В чем идея алгоритма сжатия Лемпеля—Зива?
7. Какие свойства зрения
и слуха человека учитываются при сжатии графической и звуковой информации?
1 .5.1 . Хранение информации
В основе любой информационной деятельности лежат три процесса: хранение информации, передача информации и обработка информации. По этой причине хранение, передачу и обработку информации называют основными типами информационных процессов.
В процессе хранения информация размещается на некотором носителе материальной среде, пригодной для фиксации (записи) информации.
 |
Использование бумажных носителей информации
Носителем, имеющим наиболее массовое употребление, до сих пор остается бумага. Изобретенная во П веке н. э. в Китае бумага служит людям уже 19 столетий.
Для сопоставления объемов информации на разных носителях будем пользоваться универсальной единицей байтом, считая, что один символ текста «весит» 1 байт. Нетрудно подсчитать информационный объем книги. Пусть книга содержит ЗОО страниц с размером текста на странице примерно 2000 символов. Текст такой книги имеет объем приблизительно 600 ООО байтов 586 Кб.
Что касается
долговечности хранения документов, книг и прочей бумажной продукции, то она
очень сильно зависит от качества бумаги, от красителей, используемых при записи
текста, от условий хранения. Интересно, что до середины XIX века (с этого
времени в качестве бумажного сырья начали использовать древесину) бумага
делалась из хлопка и текстильных отходов — тряпья. Чернилами служили
натуральные красители. Качество рукописных документов того времени было
довольно высоким, и они могли храниться тысячи лет. С переходом на древесную
основу, с распространением машинописи и средств копирования, с использованием
синтетических красителей срок хранения печатных документов снизился до 200—300
лет.
На первых компьютерах бумажные носители использовались для
цифрового представления вводимых данных. Это были перфокарты: картонные
карточки с отверстиями, хранящие двоичный код вводимой информации. На некоторых
типах ЭВМ для тех же целей применялась перфорированная бумажная лента.
Использование магнитных носителей информации
|
|
Теоретические основы информатики |
 |
В 20-х годах прошлого века появляется магнитная лента сначала на бумажной, а позднее на синтетической (лавсановой) основе, на поверхность которой наносится тонкий слой ферромагнитного порошка. Во второй половине ХХ века на магнитную ленту научились записывать изображение, появляются видеокамеры, видеомагнитофоны.
На ЭВМ первого и второго поколений магнитная лента использовалась как единственный вид сменного носителя для устройств внешней памяти. Любая информация в компьютере на любом носителе хранится в двоичном (цифровом) виде. Поэтому независимо от вида информации: текст это или изображение, или звук ее объем можно измерить в битах и байтах. На одну катушку с магнитной лентой, использовавшейся в лентопротяжных устройствах первых ЭВМ, помещалось приблизительно 1,5 Мб информации.
С начала 1960-х годов в употребление входят компьютерные магнитные диски: алюминиевые или пластмассовые диски, покрытые тонким магнитным порошковым слоем толщиной в несколько микрон. Информация на диске располагается по круговым концентрическим дорожкам. На первых ПК использовались гибкие
магнитные диски
(флоппи-диски) сменные носители информации с небольшим объемом памяти — до 2
Мб. Начиная с 1980-х годов, в ПК начали использоваться встроенные в системный
блок накопители на жестких магнитных дисках, или НЖМД (англ.
HDD — Hard Disk Drive). Существуют также съемные накопители на жестких магнитных дисках, подключаемые через USB-nopT.
Жесткий диск компьютера это пакет магнитных дисков, надетых на общую ось, собранных в общем корпусе с двигателем и устройством управления. Информационная емкость современных жестких дисков измеряется в терабайтах.
В банковской системе большое распространение получили пластиковые карты. На них тоже используется магнитный принцип записи информации, с которой работают банкоматы, кассовые аппараты, связанные с информационной банковской системой.
Использование оптических дисков и флеш-памяти
 |
очень
высокой плотностью. Считывание происходит в результате отражения от такой
«перфорированной» поверхности лазерного луча с меньшей энергией («холодного»
луча). Первоначально на ПК вошли в употребление оптические компакт-диски — СТ),
информационная емкость которых составляет от 190 до 700 Мб.
Во второй половине
1990-х годов появились цифровые универсальные видеодиски DVD (Digital Versatile
Disk) с большой емкостью, измеряемой в гигабайтах (до 8 Гб). Увеличение их
емкости по сравнению с СГ)-дисками связано с использованием лазерного луча
меньшего диаметра, а также двухслойной и двусторонней записи.
В настоящее время оптические диски (CD и DVD) являются наиболее надежными носителями информации, записанной цифровым способом. Эти типы носителей бывают как однократно записываемыми пригодными только для чтения, так и перезаписываемыми пригодными для чтения и записи.
В последнее время появилось
множество мобильных цифровых устройств: цифровые фото- и видеокамеры,
МРЗ-плееры, карманные компьютеры, мобильные телефоны, смартфоны, устройства для
чтения электронных книг, 
и многое другое. Все эти устройства
нуждаются в переносных носителях информации. Но так как все мобильные
устройства довольно миниатюрные, то и к носителям информации для них
предъявляются особые требования. Они должны быть компактными, обладать низким
энергопотреблением при работе, быть энергонезависимыми при хранении, иметь большую
емкость, высокие скорости записи и чтения, долгий срок службы. Всем этим
требованиям удовлетворяют флеш-карты памяти. Информационный объем флеш-карты
может составлять несколько гигабайтов.
|
|
Теоретические основы информатики |
 |
В последние годы активно ведутся работы по созданию еще более компактных носителей информации с использованием нанотехнологий, работающих на уровне атомов и молекул вещества. В результате один компакт-диск, изготовленный по нанотехнологии, сможет заменить тысячи оптических дисков. По предположениям экспертов, приблизительно через 20 лет плотность хранения информации возрастет до такой степени, что на носителе объемом примерно с кубический сантиметр можно будет записать каждую секунду человеческой жизни.
Организация информационных хранилищ
Процесс хранения информации связан не только с ее размещением на носителях. При больших объемах информации создаются информационные хранилища, для которых важными свойствами является организация данных: их упорядоченность, внутренняя структура. От способа организации данных зависит возможность Доступа к информации, производимого при поиске и коррекции данных. Проблемы оптимальной организации данных решаются как в традиционных «бумажных» хранилищах (архивах, библиотеках), так и в компьютерных базах данных.
|
Информационные процессы |
|
Система основных понятий
|
|
Хранение информации |
||||||
|
|
Носители информации |
||||||
|
Нецифровые |
Цифровые (компьютерные) |
||||||
|
Исторические: камень, дерево, папирус, пергамент, шелк... Современные: бумага |
Магнитные |
Оптические |
Флеш-носители |
||||
|
Ленты |
диски |
Карты |
CD |
DVD |
Флеш- карты |
Флешбрелоки |
|
|
Факто ы качества носителей |
|||||||
|
Вместимость — плотность хранения данных, объем данных |
Надежность хранения — максимальное время сохранности данных, зависимость от условий хранения |
||||||
|
Наибольшей надежностью на сегодня обладают оптические носители CD и DVD |
|||||||
|
Перспективные виды носителей: носители на базе нанотехнологий |
|||||||
Вопросы и задания
1. Какая, с вашей точки зрения, сохраняемая информация имеет наибольшее значение для всего человечества; для отдельного человека?
2. Назовите известные вам крупные хранилища информации.
З. Можно ли человека назвать носителем информации?
4. Где и когда появилась бумага? Подготовьте сообщение.
5.
Когда была
изобретена магнитная запись? Какими магнитными носителями вы пользуетесь или
пользовались? Подготовьте презентацию. 
6. Какое техническое изобретение позволило создать оптические носители информации? Назовите типы оптических носителей.
7. Назовите сравнительные преимущества и недостатки магнитных и оптических носителей.
8. Что означает свойство носителя «только для чтения»?
9. Какими устройствами, в которых применяются флеш-носители, вы пользуетесь? Какой у них информационный объем?
10. Какие перспективы, с точки зрения хранения информации, открывают нанотехнологии? Подготовьте доклад. Используйте ресурсы Интернета.
1 .5.2. Передача информации
Передача информации — это процесс распространения инфорО мации от источника к приемнику через определенный канал связи.
В отличие от процесса передачи материальных объектов, при передаче информации источник не лишается передаваемой информации. Поэтому можно сказать, что результатом процесса передачи информации является ее размножение, копирование. При этом возникает проблема адекватности копии оригиналу, которая может быть нарушена из-за искажений или потери части информации в процессе передачи.
В параграфе 1.4.1 уже рассказывалось об истории развития технических средств передачи информации, о способах передачи информации посредством непрерывного и дискретного сигналов.
|
|
Теоретические основы информатики |
 |
Модель передачи информации
Клод Шеннон предложил модель процесса передачи информации по техническим каналам связи, представленную схемой на рис. 1.19.
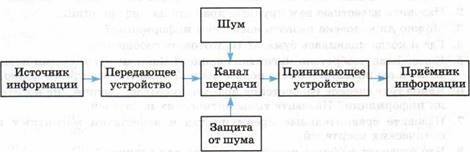
Рис. 1.19. Техническая система передачи информации
Работу такой схемы можно пояснить на знакомом всем процессе разговора по проводному телефону. Источником информации
является говорящий человек. Передающим
устройством — микрофон телефонной трубки, с помощью которого звуковые волны
(речь) преобразуются в электрические сигналы. Канал передачи здесь телефонная
сеть: провода, коммутаторы телефонных узлов, через которые проходит сигнал.
Принимающее устройство 
лефонная трубка (наушник), в котором
пришедший электрический сигнал превращается в звук. Приемником, или адресатом
передаваемого сообщения, является человек.
В современных компьютерных системах связи источниками и приемниками информации являются компьютеры. Между ними происходит передача кода, заключающего в себе содержание сообщения. Передающее устройство производит преобразование двоичного компьютерного кода в физический сигнал того типа, который передается по каналу связи. В принимающем устройстве происходит обратное преобразование передаваемого сигнала в компьютерный код. Например, при использовании в компьютерных сетях телефонных линий функции принимающего/передающего устройства выполняет прибор, который называется моДемом.
 |
Иногда, беседуя по телефону, мы слышим шум, треск, мешающие понять собеседника, или на наш разговор «накладывается» разговор других людей.
Наличие шума приводит к потере части передаваемой информации. В таких случаях необходима защита от шума.
Для защиты в первую очередь применяются технические способы защиты каналов передачи от воздействия шумов. Такие способы бывают самые разные: например, использование экранированного кабеля вместо «голого» провода; применение разного рода фильтров, отделяющих полезный сигнал от шума, и пр.
Другой способ борьбы с шумом это внесение
избыточности в передаваемое сообщение. За счет избыточности потеря какойто
части информации при передаче может быть компенсирована. 
Например, если при
разговоре по телефону вас плохо слышно, то, повторяя каждое слово дважды, вы
имеете больше шансов на то, что собеседник поймет вас правильно.
Теорема Шеннона
Скоростью передачи информации называется
количество информации, передаваемое за единицу времени. Разработчикам
технических систем передачи информации приходится решать две взаимосвязанные
задачи: как обеспечить наибольшую скорость передачи информации и как уменьшить
потери информации при передаче. Клод Шеннон был первым ученым, взявшимся за
решение этих задач и создавшим новую для того времени науку 
теорию
информации.
Шеннон определил способ измерения количества информации, передаваемой по каналам связи. Он ввел понятие пропускной споО собности канала связи как максимально возможной скорости передачи информации. Эта скорость измеряется в битах в секунду (а также килобитах (Кбит) в секунду, мегабитах (Мбит) в секунду
Пропускная способность канала связи зависит, во-первых, от его технической реализации. В компьютерных сетях используются следующие виды связи:
|
|
Теоретические основы информатики |
электрическая связь (телефонные
линии, электрический кабель); 
оптическая связь (оптоволоконный кабель); 
радиосвязь (радиорелейные линии,
спутниковая связь).
Скорость передачи информации по аналоговым телефонным
каналам составляет десятки Кбит/с, по каналам радиосвязи 
сотни Кбит/с,
а по оптоволоконным линиям связи — до десятка Гбит/с.
Во-вторых, пропускная способность канала зависит от уровня
шума. Точнее говоря, она зависит от отношения уровня шума к уровню сигнала.
Если амплитуду электрических помех обозначить буквой (в вольтах), а буквой А
обозначить амплитуду полезного сигнала, то значение L/A есть отношение уровня
шума к уровню сигнала. Чем больше эта величина, тем больше шум перекрывает
сигнал. Пропускная способность канала связи существенно зависит от уровня
искажений сигнала, который вносят шумы.
В 1950-х годах Клод Шеннон сформулировал фундаментальную теорему, носящую его имя.
Теорема Шеннона: всякий зашумленный канал связи харакО теризуется своей предельной скоростью передачи информации (пропускной способностью), называемой пределом Шеннона.
При скоростях, превышающих этот предел, неизбежны ошибки в передаваемой информации. Зато при скоростях, не превышающих предел Шеннона, можно обеспечить сколь угодно малую вероятность ошибки за счет соответствующего способа коДирования.
Защита от шума
Если по каналу передается аналоговый сигнал, например телефонный разговор, то при небольших шумах слушателю все же удается понять содержание сообщения благодаря избыточности, существующей у любого естественного языка. Для систем дискретной цифровой связи потеря даже одного бита при использовании неизбыточного кода может привести к полному обесцениванию информации.
Избыточность — это та цена, которую приходится платить за достоверность информации. Вот простая идея коррекции ошибок: каждый байт данных передавать три раза подряд. Принять тот код, который дважды повторился в этой тройке.
|
|
89 |
|
Информационные процессы |
|
Применение метода ЛТ-кратного дублирования кода увеличивает избыточность данных в лт раз и, как следствие, во столько же раз уменьшает скорость передачи. Проблема, которая многие годы решалась специалистами в области теории связи, минимизация избыточности, автоматическое исправление (коррекция) ошибок при передаче данных.
Для контроля и коррекции ошибок требуется специальное кодирование передаваемых данных. Наиболее простым вариантом контроля является использование контрольной суммы. Алгоритм вычисления контрольной суммы такой, что любое изменение кода сообщения приводит к изменению контрольной суммы. Всё сообщение разбивается на порции блоки. Для каждого блока вычисляется контрольная сумма, которая передается вместе с данным блоком. В месте приема сообщения заново вычисляется контрольная сумма принятого блока, и если она не совпадает с первоначальной суммой, то передача данного блока повторяется. Так будет происходить до тех пор, пока исходная и конечная контрольные суммы не совпадут.
Контрольная сумма позволяет установить наличие ошибки
в блоке, но ее исправление происходит дорогостоящим способом 
повторной
передачей данных по каналу связи. Другой подход к исправлению ошибок
заключается в использовании корректирующих кодов. Их также называют кодами с
коррекцией ошибок или помехоустойчивыми кодами. Именно использование таких
кодов позволяет приблизиться к пределу Шеннона. О таких кодах мы поговорим в
следующем параграфе.
О Система основных понятий
|
Передача информации в технических системах связи |
|||||
|
Модель Клода Шеннона |
|||||
|
Источник, передающее устройство |
Процесс передачи по каналу связи |
Принимающее устройство, приемник |
|||
|
Воздействие шумов на канал связи |
Защита от ш а |
||||
|
Теорема Шеннона: всякий зашумленный канал связи характеризуется своей преДельной скоростью переДачи информации (пропускной способностью) |
|||||
|
Способы защиты информации от потерь при воздействии шума |
|||||
|
Технические средства защиты: экранирование, фильтрация и др. |
Защита путем внесения избыточности |
||||
|
Дублирование данных |
Вычисление контрольной суммы |
Помехоустойчивое кодирование |
|||
Вопросы и задания
|
|
Теоретические основы информатики |
1.
 |
2. Замечали ли вы факты потери информации?
3. Что такое шум по отношению к системам передачи данных? Каковы источники шума? Приведите примеры.
О 4. Что такое пропускная способность канала связи и от чего она зависит?
5. Как вы думаете, есть ли разница между понятиями «потеря данных» и «потеря информации»? О чем идет речь в теореме Шеннона: о потере данных или о потере информации?
б. Какие существуют способы борьбы с шумом?
7.
Какой метод борьбы
с шумом эффективнее: регулярное дублирование данных или блочное контрольное
суммирование? Как может зависеть эффективность защиты данных от размера блоков
при использовании контрольного суммирования? Обоснуйте ответ.
8. Пропускная способность канала связи составляет 100 Мбит/с. Уровень шума пренебрежимо мал (например, оптоволоконная линия). Определите, за какое время по каналу будет передан текст, информационный объем которого составляет 100 Кб.
О 9. Пропускная способность канала связи равна 10 Мбит/с. Канал подвержен воздействию шума, поэтому избыточность кода передачи составляет 20 0/0. Определите, за какое время по каналу будет передан текст, информационный объем которого составляет 100 Кб.
1 .5.3. Коррекция ошибок при передаче данных
Помехоустойчивый код Хемминга
Поясним суть помехоустойчивого кодирования на простом примере. Рассмотрим идею широко используемого кода Хемминга. В нем используются следующие основные понятия: коДовое слово, расстояние мелсДу словами.
ЕоДовое слово состоит из исходного кода и дополнительных символов, присоединяемых к исходному коду. Пусть передается сообщение, состоящее только из десятичных цифр. Весь такой алфавит можно закодировать, используя двоично-десятичный четырехразрядный код (второй столбец табл. 1.9). В третьем столбце таблицы приведены коДовые слова, в которых к двоичным кодам десятичных цифр добавлены три дополнительных двоичных разряда.
Таблица 1.9
|
Информационные процессы |
|
 |
|
Символ |
Двоичный код |
Кодовое слово |
|
|
0000 |
0000 000 |
|
1 |
0001 |
0001 111 |
|
2 |
0010 |
0010 110 |
|
з |
0011 |
0011 001 |
|
4 |
0100 |
0100 101 |
|
5 |
0101 |
0101 010 |
|
|
0110 |
0110 011 |
|
7 |
0111 |
0111 100 |
|
8 |
1000 |
1000 011 |
|
9 |
1001 |
1001 100 |
Расстоянием между Двумя словами называется количество позиций, в которых символы одного слова не совпадают с символами другого слова. Например, между кодовыми словами десятичных цифр 5 и 6 расстояние равно трем:
5: 0101010
6: 0110011
Между цифрами 7 и 8 расстояние равно семи. Минимальное расстояние между кодовыми словами в данной таблице равно Предположим, что нами получено сообщение, закодированное кодом Хемминга. Разделим это сообщение на семибитовые слова. Если полученное слово совпадает с кодовым словом из таблицы 1.9 (расстояние между ними равно нулю), то передача произошла без ошибок. Если в табл. 1.9 существуют слова, расстояния от которых до полученного слова равны 1 или 2, то данное кодовое слово содержит ошибки в одной или двух позициях. Это следует из того, что минимальное расстояние между разными символами должно быть не меньше З.
Слово, в котором обнаружена одна ошибка, заменяется на блиэкайшее к нему из кодовой таблицы. Весьма высока вероятность того, что именно оно было искажено. Если минимальное расстояние между полученным словом и словами в таблице равно двум, то считается, что автоматически код исправить нельзя.
|
|
Теоретические основы информатики |
 |
В
нашем примере, при минимальном расстоянии между кодовыми словами, равном трем,
алгоритм коррекции позволяет исправлять одну ошибку в кодовом слове. В общем
случае, если R — минимальное расстояние между словами в таблице Хемминга, то
автоматической коррекции поддаются [(R— 1)/2] ошибок в кодовом слове
(квадратные скобки обозначают выделение целой части числа).
Пример. По каналу связи получено сообщение в форме следующего кода:
0100101.
Первое слово совпадает с кодовым словом цифры 8. Второго слова нет в кодовой таблице. Ближайший к нему код находится
дующем слове также обнаружена ошибка.
Ближайшее слово 
0110011. Это код цифры 6. Последнее слово
— код цифры 4. Следовательно, передано сообщение: 8164.
Показанный в примере процесс контроля и коррекции по таблице кода Хемминга легко поддается программированию. Поэтому исправление ошибок, возникших при передаче данных, можно производить автоматически на принимающем сообщение компьютере.
Можно определить коэффициент преобразования коДа как отношение длины преобразованного кода к длине исходного кода. Для преобразования сжатия (см. параграф 1.4.5) эту величину мы называли коэффициентом сжатия. Его значение меньше единицы. Применение помехоустойчивого кодирования ведет к «растяжению» кода. Для рассмотренного примера значение коэффициента преобразования кода равно 7/4 = 1,75. Увеличение размера кода на 7596— довольно высокая цена за возможность исправления одной ошибки в слове!
Построение корректирующих кодов с заданным минимальным
расстоянием между кодовыми словами является сложной задачей. Разработаны
алгоритмы, успешно решающие эту задачу1)
В нашем примере рассмотрен четырехразрядный код,
расширенный тремя битами, с минимальным расстоянием между словами, равным трем.
В международных системах связи используется 235-разрядный код с расширением 20
битов и минимальным расстоянием между словами, равным 7. Такой код позволяет
обнаруживать до 6 ошибок, допущенных в слове, и гарантированно (автоматически)
исправлять слова, содержащие не более трех ошибок. Вычислим коэффициент
преобразования кода, о котором говорилось выше. Он равен: (235 + 20)/235 = 255/235
1,085. Длина кода увеличивается всего на 8,5 0/0 !
Учимся программировать
(подпрограмма-функция)
|
Информационные процессы |
|
 |
1) код верный: символ Х;
2) код исправлен: символ Х; З) код неверный.
Первый ответ выводится в случае, если в кодовой таблице находится символ Х, расстояние между кодовым словом которого и введенным кодом равно нулю. Второй ответ выводится, если ближайшее расстояние между кодовым словом символа Х и введенным кодом равно единице. Третий ответ выводится в случае, если ближайшее расстояние между введенным кодовым словом и кодовыми словами табл. 1.9 больше единицы.
В приведенной программе есть новые элементы Паскаля,
с которыми вы раньше не встречались. Обсудим их. Для хранения таблицы кода
Хемминга используется Двумерный массив с именем Тат. Он содержит десять строк,
нумеруемых от О до 9, и два столбца с номерами 1 и 2. В первом столбце
находятся кодируемые символы (цифры от О до 9), во втором столбце 
1 ) Подробно см.: Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. — М.: Техносфера, 2005.
соответствующие кодовые слова согласно табл. 1.9. Таблица содержит постоянные значения, поэтому в программе она описана не как переменная, а как константа (после слова Const).
Семиразрядные целые числа не укладываются в диапазон типа
integer. Поэтому тип элементов таблицы 10ngint длинный целый тип. Число такого
типа занимает в памяти 4 байта и может принимать значения в диапазоне от —2 31
до 2 31 —1
Значения констант указываются в тексте программы в круглых
скобках после знака «=». Значения двумерного массива записываются построчно
через запятую. Каждая строка заключается в круглые скобки.
Для вычисления расстояния между двумя семиразрядными кодовыми словами в программе используется функция с именем Distance. Это нестандартная функция, которая используется только в данной программе. Описание функции располагается в разделе описаний программы и имеет следующий формат:
Function <имя функции> «описания
параметров>) : <тип функции>; <внутренние описания> ; begin
|
|
Теоретические основы информатики |
 |
Параметры функции это ее аргументы,
исходные данные, с которыми работает функция (переменные Х, У). Они называются
формальными параметрами и позже, при обращении к функции получат конкретные
значения того же типа — фактические значения параметров.
Тип функции — это тип ее результата. Результат вычисления функции присваивается переменной с тем же именем, что имеет функция, — Distance. Поскольку результат функции число в диапазоне от О до 7, достаточно типа byte.
Алгоритм функции Distance построен на поразрядном сравнении цифр двух семиразрядных кодов Х и У, справа налево. Переменой К, в которой хранится расстояние между кодами, сначала присваивается значение 7, а затем, при совпадении каждой пары разрядов, вычитается единица. Если совпадут все разряды, расстояние будет равно нулю, если не совпадет ни одной пары, останется равным 7.
В основной части программы реализован стандартный алгоритм поиска минимального значения (переменная min) и соответствующего ему номера элемента (переменная imin). Элементы либо в результате полного совпадения (расстояние равно О), либо при наличии одной ошибки (расстояние равно 1).
Program Hemming ;
Const Тат:
array [О. . 9,1. .2] 0f 10nqint 
Таблица кода Хемминга}
( (0,0000000) ,
(2,0010110) ,
(3, 0011001) ,
(5,0101010) ,
(6,0110011) ,
(8, 1000011) ,
(9, 1001100) ) ;
Var 1, min, imin, Г): byte; cod: 10ngint;
Eunction Distance (Х, У; 10ngint) :
byte; 
Функция вычисления расстояния между двумя кодовыми словами) var ј, К:
byte; begin
|
Информационные процессы |
|
 |
{
Начальное значение параметра расстояния между словами) for -ј to 7
do begin if (Х mod 10 mod 10) { сравнение младших разрядов 
then
К:=К—1; 
Вычитание 1 при совпадении}
Х:=Х div 10; У:=У div 10 
Отбрасывание
младших разрядов
|
end ; |
|
|
Distance : |
|
end; {КОНеЦ функции} begin
Write ( т код=') ; Read1n (cod) ; (Ввод семиразрядного кода) min:= Distance (cod, ТаЬ1 [0,2) ) ; imin : ; for i:=1 Ео 9 do begin
D : =Distance (cod, ТаЬ1 [1, 2) )
; [Вычисление минимального) if D<min then { расстояния — переменная min 
begin
{и соответствующего ему 
min:=D; imin:—i { номера строки в таблице)
end {ТаЬ1 — переменная imin} end;
{Выбор варианта ответа} if min=O
then Write1n ( ' Код верный: символ 
ТаЬ1 [imin, 1] ) e1se if min=1 then
Write1n ( ' Код исправлен: символ , ТаЬ1 [imin, 1] ) else Write1n ( ' Код
неверный ' ) end.
Тестирование программы нужно организовывать таким образом, чтобы проверялась правильность получения всевозможных вариантов результата. Поэтому выполним три теста: для верного кода символа; для кода, поддающегося коррекции (минимальное расстояние равно 1), и для ошибочного кода (минимальное расстояние больше 1).
Тест 1. Расшифруем код: 0101010.
код=0101010 
код верный : симв ол 5 .
тест 2. Расшифруем код: 0100010 код—-0100010 код исправлен : символ 5 .
тест З.
Расшифруем код: 0100011 код=0100011 код
|
|
Теоретические основы информатики |
Все тесты выполнились верно.
Еще раз подчеркнем, что данная программа всего лишь модель
работы алгоритма Хемминга.
О Система основных понятий
|
Коррекция ошибок |
|
|
Код Хемминга применяется для помехоустойчивого кодирования |
|
|
Кодовое слово: |
Расстояние между кодовыми словами: |
|
исходный двоичный код + добавочный код меньшей длины |
количество позиций, в которых символы одного слова не совпадают с символами другого слова |
|
Кодовое слово содержит ошибки, если минимальное расстояние между ним и кодовыми словами таблицы Хемминга меньше минимального расстояния между кодами таблицы |
|
|
Если R — минимальное расстояние между словами в таблице Хемминга, то автоматической коррекции поддаются [(R—1)/2] ошибок в кодовом слове |
|
Вопросы и задания
1. Из чего состоит помехоустойчивый код Хемминга?
2. Что такое расстояние между кодовыми словами?
З. В каком случае принятый код считается верным?
4. В каком случае ошибочный код допускает автоматическую коррекЦИК)?
Практикум. Раздел 2 «Кодирование»
1 .5.4. Обработка информации
Виды обработки информации
Процесс обработки информации производится в соответствии с определенными правилами некоторым объектом (например, человеком или компьютером). Будем его называть исполнителем обработки информации.
|
|
97 |
|
Информационные процессы |
|
Информация, которая подвергается обработке, представляется в виде исходных данных. На рисунке 1.20 в схематическом виде обозначены основные составляющие процесса обработки информации и их взаимодействие.
Рис. 1.20. Модель обработки информации
В дальнейшем, анализируя процессы обработки информации, мы будем употреблять термин «задача», рассматривая обработку информации как процесс решения некоторой информационной задачи. Все множество задач обработки информации можно разделить на четыре группы:
1) получение новой информации, не содержащейся в исходных данных (например, решение математической задачи);
2) изменение формы представления информации (например: кодирование, шифровка, преобразование в табличную или графическую форму);
З) структурирование данных (например, упорядочение по какому-либо признаку, каталогизация);
4) поиск в массиве данных по некоторому критерию (например, поиск в справочнике, в словаре, в каталоге).
Правила — это информация процедурного типа. Они содержат сведения для исполнителя о том, какие действия требуется выполнить, чтобы решить задачу.
Все перечисленные виды обработки информации может выполнять как человек, так и компьютер. В чем состоит принципиальное различие между процессами обработки, выполняемыми человеком и машиной?
|
|
Теоретические основы информатики |
 |
О Компьютер формальный исполнитель обработки инфор-
мации.
Важнейшим условием для успешности выполнения обработки информации является полнота исходных Данных. Говоря другими словами, исходных данных должно быть достаточно для решения поставленной задачи. Например, если даны длины трех сторон треугольника, то можно вычислить площадь этого треугольника по формуле Герона. Но если известны длины только двух сторон, то площадь вычислить нельзя. Нельзя в телефонном справочнике найти номер телефона человека, у которого вы знаеге только имя и отчество, но не знаете фамилии.
Об алгоритмах и исполнителях
Для обозначения формализованных правил, определяющих последовательность шагов обработки информации, в информатике используется понятие «алгоритм».
Из курса информатики 7—9 классов вы знаете, что слово «алгоритм» произошло от имени выдающегося математика средневекового Востока Мухаммеда ибн Муса аль-Хорезми, описавшего
еще в IX веке правила выполнения
вычислений с многозначными десятичными числами. Правила сложения, вычитания,
умножения и деления столбиком, которым вас учили в младших классах, — это
алгоритмы аль-Хорезми.
Исполнителя обработки информации (данных) называют также исполнителем алгоритма. С этим понятием вы знакомы из курса Аль-Хорезми информатики 7—9 классов. (783-850 гг. н. э.)
Компьютер это
автоматический, программно управляемый исполнитель алгоритмов обработки
информации.
Алгоритм, записанный на языке программирования для компьютера, называется программой.
|
Информационные процессы |
|
 |
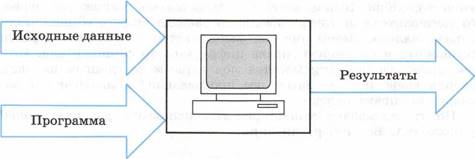
Рис. 1.21. Модель обработки информации компьютером
Об алгоритмической множественности
Любая ли задача обработки информации имеет алгоритмическое решение? Оказывается, что нет! В теории алгоритмов известен ряд алгоритмически неразрешимых заДач [4] ). Примеры таких задач: задача Лейбница о проверке правильности математических теорем; проблема останова; проблема Гильберта об определении существования целочисленных решений для любого алгебраического уравнения с целыми коэффициентами.
Задачу, для решения которой можно построить алгоритм, называют алгоритмически разрешимой задачей. Как правило, для решения одной и той же задачи можно построить множество различных алгоритмов. Ситуация подобна той, что для перемещения на какой-то местности из одного места в другое может существовать множество вариантов пути.
Рассмотрим пример. Все вы хорошо знаете алгоритм умножения многозначных целых чисел. Будем называть его в дальнейшем алгоритмом аль-Хорезми. Вот пример реализации такого алгоритма:
1 8
5 4
7 7 4
|
|
Теоретические основы информатики |
Словесно описать его можно так. Два сомножителя записываются в столбик. Выполняется последовательное умножение первого сомножителя на цифру младшего разряда второго сомножителя справа налево. Затем так же выполняется умножение первого сомножителя на вторую справа цифру второго сомножителя. Второе произведение записывается под первым со сдвигом на один разряд влево и т. д. Затем все произведения складываются поразрядно справа налево.
Но ту же задачу можно решить,
используя русский метод умножения. Вот его реализация:
|
|
|
|
нечетное |
|
36 |
21 |
нечетное |
|
|
72 |
10 |
|
|
|
144 |
5 |
нечетное |
|
|
288 |
2 |
|
|
|
576 |
1 |
нечетное |
|
|
Результат: |
774 |
|
|
Словесное описание алгоритма русского метода такое: производится последовательное умножение первого сомножителя на 2 и одновременно целочисленное деление на 2 второго сомножителя. С полученным результатом производятся такие же действия. Процесс заканчивается, когда второй сомножитель становится равным
единице. Затем складываются все значения первого сомножителя, соответствующие нечетным значениям второго сомножителя. Наверно, вы согласитесь, что, с точки зрения прилагаемых усилий, при ручном счете алгоритм аль-Хорезми реализовать легче, чем русский алгоритм.
|
Информационные процессы |
 |
 |
Учимся программировать
(целочисленная арифметика)
Рассмотрим две программы на Паскале, реализующие алгоритм аль-Хорезми и русский метод умножения целых многозначных чисел. Конечно, в Паскале можно за одну операцию выполнить умножение многозначных чисел. Но наша цель состоит в демонстрации алгоритмического различия между русским методом и методом аль-Хорезми.
|
Программа русского метода: |
Программа метода аль-Хорезми: |
|
Program Russian method; Var М, N, Ми 1: integer; begin 1—й сомножитель } Write Read1n (М) ; 2-й сомножитель } Write ( Read1n (Н) ; Write (М, ' * ' N, ' переменная для произведения Миш : whi1e N>=1 do begin if
(N mod 2 1) then Ми 1 ; =Ми1+М; div 2; Write1n (Миш ) end. |
Program А 1 Horezmi ; Var М, ГМ, Ми 1, ф: integer; begin Write ( 'М=' ) ; Read1n (М) ; Write ( 'N=' ) ; Read1n (N) ; Write (М, ' N, while N>=1 do begin
ми1 (Ы mod 10) div 10; Write1n (Ми 1) end. |
Изучите внимательно эти программы. Ваших знаний программирования уже вполне достаточно, чтобы понять их смысл без комментариев. Интерфейс с пользователем у обеих программ совершенно одинаковый. Например, возможен такой вариант выполнения: м=18 N=43
Можно ли сказать, какая из программ лучше, какая хуже? Всё зависит от критерия оценки. Основными критериями оптимальности программ являются время выполнения на компьютере и объем используемой памяти, поскольку исполнителем программ является компьютер.
Объем памяти, используемой под данные, в этих программах различается незначительно. В первой программе три переменные: М, N, МТ, во второй четыре переменные: М, N, Ми, Q.
|
|
Теоретические основы информатики |
|
Подсчитаем количество вычислительных операций внутри циклов
(ограничимся только арифметическими операциями). В первой программе их 4, во
второй б. Следовательно, в циклической части первой программы будет выполнено 6
• 4 = 24 вычислительные операции, во второй 
12 операций.
Следовательно, вторая программа будет выполняться в два раза быстрее.
Подсчитаем число операций при лт = 1024 = 2 10 . В первой программе: 10 • 4 = 40. Во второй программе: 4 • б = 24. Выигрыш во времени также приблизительно в два раза больше.
В теории алгоритмов используется понятие «временная сложность» алгоритма. Чем время выполнения алгоритма (программы) больше, тем больше его временная сложность. Из проведенного анализа следует, что временная сложность русского алгоритма выше, чем алгоритма аль-Хорезми. Вспомните, что и для ручного выполнения мы оценивали русский алгоритм как более сложный. Именно поэтому русский алгоритм не изучается в школьной ма-
|
Информационные процессы |
|
 |
|
Обработка информации |
|||||
|
Модель системы обработки информации: на входе исполнителя — исходные данные и правила обработки, на выходе ез льтаты об аботки |
|||||
|
Виды обработки информации |
|||||
|
Получение новой ин- формации (новых дан- ных) |
Изменение формы представления ин- формации |
Структурирование данных |
Поиск данных |
||
|
Исполнитель обработки |
|||||
|
Человек |
Автомат (компьютер) |
||||
|
Неформальный исполнитель, способный самостоятельно вы- рабатывать правила обработки |
Компьютер — это автоматический, программно управляемый исполнитель алгоритмов обработки информации |
||||
|
Правила обработки: описание последовательности действий исполнителя обработки информации (синонимы: алгоритм, программа) |
|||||
|
Алгоритмическая множественность |
|||||
|
Задача, для решения которой нель- зя построить алгоритм, называется алгоритмически неразрешимой |
Для алгоритмически разрешимой задачи существует множество алгоритмов ее решения |
||||
|
Временная сложность алгоритма определяется временем работы испольнителя и его выполнении |
|||||
Вопросы и задания
1. Приведите примеры процессов обработки информации, которые чаще всего вам приходится выполнять во время учебы. Для каждого примера определите исходные данные, результаты и правила обработки. К каким вариантам обработки относятся ваши примеры?
2. Если вы решаете задачу по математике или физике и при этом используете калькулятор, то какова ваша функция в этом процессе и какова функция калькулятора?
З. Определите полный набор исходных
данных для решения задач: под
счет сдачи за покупку кассовым аппаратом в магазине; подсчет расхода
горючего при поездке на автомобиле; определение времени вы
хода из дома для того, чтобы успеть
к началу сеанса в кинотеатре.
4. Что означают словосочетания:
формальное исполнение алгоритма, формальный исполнитель?
5. Опишите словесно алгоритм деления с остатком одного целого числа на другое.
Практикум. Раздел 5 «Программирование»
1 -6.1 . Логика и логические операции
История логики
Логика наука о формах и законах человеческого мышления (рассуждения). Термин происходит от греческого слова «логос», что значит «рассуждение», «речь».
Логика древняя наука, появившаяся
приблизительно в IV веке до нашей эры. На Востоке логика развивалась в Китае и
в Индии. В Европе развитие логики исходит из Древней Греции.
Основателем логики принято считать греческого философа
Аристотеля. Аристотель первым систематизировал доступные зна
ния о логике,
обосновал формы и правила логического мышления. Результаты своих исследований
Аристотель описал в цикле сочинений под общим названием «Органон».
|
|
Теоретические основы информатики |
Логика Аристотеля анализирует рассуждения
в форме человеческой речи на естественАристотель ном языке. Мыслящий человек
оперирует (384-322 гг. некоторыми понятиями, отражающими свойдо н. э.) ства
реальных объектов, отличающие одни объекты от других. Рассуждая о чем-то,
человек производит высказывания (суждения). Высказывание — это утверждение,
которое может быть либо истинным, либо ложным. Например, истинность
высказывания «На улице идет дождь» зависит от состояния погоды. Это
высказывание может быть в одном случае истинным, а в другом 
ложным. А
высказывание «Луна спутник Земли» является всегда истинным. Приведенные примеры
являются простыми выО сказываниями. Сложные (составные) высказывания
составляются из простых высказываний, соединенных логическими связками: «и»,
«или», «не», «если то...» и др.
Умозаключение это процесс получения
нового высказывания в результате анализа данных высказываний. Согласно логике
Аристотеля, результат умозаключения определяется логической формой
высказывания. Поэтому логика Аристотеля называется формальной логикой.
Аристотель сформулировал законы формальной
логики, со-
гласно которым определяется истинность сложных высказываний. Например, согласно закону исключенного третьего, всегда истинным будет следующее высказывание: «На улице идет дождь или на улице не идет дождь» (т. е. третьего не дано). А высказывание «На улице идет дождь и на улице не идет дождь» будет всегда ложным.
В XIX веке в
математической науке возникает новый раздел — алгебра логики. Основатель этой
науки английский математик Джордж Буль.
|
Логические основы обработки информации |
|
Алгебра логики
оперирует с логическими величинами, которые могут принимать всего два значения:
«истина» и «ложь». Следовательно, согласно Аристотелю, каждая такая величина
может быть сопоставлена некоторому высказыванию. Однако алгебра логи-
|
ки это формализованная математическая |
Джордж Буль |
|
дисциплина, поэтому логическая величина не должна обязательно иметь конкретный содер- |
(1815-1864) |
жательный смысл.
Джордж Буль впервые применил алгебраические методы для
решения традиционных логических задач, которые до этого решались методами рассуждений, согласно формальной логике Аристотеля.
В алгебре логики логические величины (как и в алгебре чисел) обозначаются символическими (буквенными) именами: х, а, yr, и т. п. Алгебра чисел работает на числовом множестве значений величин, с которыми она оперирует. Множество чисел бесконечно. Алгебра логики работает на множестве, состоящем всего из двух значений: «истина» и «ложь». Их еще называют значениями истинности.
Логические операции
Во всякой алгебре определяется множество допустимых операций над величинами и правила их выполнения. В алгебре чисел это алгебраические (арифметические) операции. В алгебре логики таклсе имеются свои операции логические операции.
знакомы три из них:
В таблице 1.10 приведены все шесть логических операций с указанием принятых для них в математике символьных обозначений.
Таблица 1.10
Логические операции
|
Логическая операция |
Математический знак |
В естественной речи |
|
Конъюнкция, логическое умножение |
|
Связка «и» |
|
Дизъюнкция, логическое сложение |
|
Связка «или» |
|
Отрицание, инверсия |
|
Частица «не» |
|
Разделительная дизъюнкция, исключающее ИЛИ, сложение по модулю 2 |
|
Оборот: либо..., либо... |
|
Импликация, следование |
|
Оборот: если... то.... |
|
Эквивалентность, равносильность, равнозначность |
|
Обороты: тогда и только тогДа; необхоДимо и Достаточно |
|
|
Теоретические ОСнОвы информатики |
 |
<1-й операнд> <знак операции> «(2-й
операнд>
Например: А & В, Х У и т. п. Операция отрицания является одноместной, следовательно, применяется к одному операнду, например: —А или А.
Все варианты результатов выполнения логических
операций для различных значений операндов приведены в табл. 1.11. Такая таблица
называется таблицей истинности.
Таблица 1.11
Таблица истинности логических операций
|
А |
В |
А |
|
ТВ |
АЭВ |
А-+В |
АНВ |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Операция отрицания изменяет значение логической величины на противоположное: не истина ложь; не ложь истина.
Результатом логического умножения будет «истина» тогда и только тогда, когда истинны значения обоих операндов.
Результат логического сложения «ложь» тогда и только тогда, когда оба операнда имеют значение «ложь».
Операция «исключающее или», в отличие от «или» (дизъюнкции), принимает еще значение «ложь», когда оба операнда истинны. Например, пусть имеется высказывание «Учебник по информатике стоит на третьей полке книжного шкафа или стоит на четвертой полке книжного шкафа». Одна и та же книга не может одновременно стоять на двух полках. Поэтому в реальной ситуации истинным это высказывание будет в двух случаях: либо учебник стоит на третьей полке, либо на четвертой полке.
Операция следования (импликация) А В трактуется следующим образом: если А, то В. Можно еще сказать так: из А следует В. Импликация используется в высказываниях, подчеркивающих зависимость одного события от другого.
|
Логические основы обработки информации |
|
 |
следствием или заключением. Из истинной посылки
не может следовать ложное заключение. Результат А -» В будет ложным тогда и
только тогда, когда А равно «истина», а В — «ложь».
Операция эквивалентности используется в логике тогда, когда необходимо выразить взаимную обусловленность двух утверждений. Многие математические теоремы формулируются с использованием оборотов «тогда и только тогда» или «необходимо и достаточно». Например: «Квадратное уравнение имеет действительные корни тогда и только тогда, когда его дискриминант положительный». Данное высказывание истинно, потому что истинны одновременно два высказывания: «Если квадратное уравнение имеет действительные корни, то его дискриминант положительный» и «Если дискриминант квадратного уравнения положительный, то оно имеет действительные корни».
Обозначим буквой А высказывание
«Квадратное уравнение имеет действительные корни», а буквой В высказывание
«Квадратное уравнение имеет положительный дискриминант». Тогда сформулированная
выше теорема с использованием знака эквивалентности запишется так: А е» В , что
читается как «А эквивалентно В» или «А равнозначно В».
О Пример 1. Шахматы
Есть четыре друга: Антон, Виктор, Семён и Дмитрий. Относительно их умения играть в шахматы, справедливы следующие высказывания:
1) Семён играет в шахматы;
2)
если Виктор не играет в шахматы, то играют Семён и Дмитрий;
З) если Антон или Виктор играет, то Семён не играет.
Преобразуем эти высказывания в алгебраическую форму. Введем логические переменные для обозначения четырех простых высказываний:
А = «Антон играет в шахматы»;
В = «Виктор играет в шахматы»; С = «Семён играет в шахматы»;
D = «Дмитрий играет в шахматы».
|
|
Теоретические основы информатики |
 |
следования.
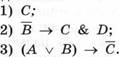
О Пример 2. Поездка на дачу
В семье есть мама, папа, дочь и собака. Рассматривается вопрос о поездке некоторых членов семьи на дачу. Если мама поедет на дачу, то поедет и папа. Дочь поедет на дачу тогда и только тогда, когда поедут мама, папа и собака. Собака поедет на дачу только тогда, когда поедет дочь или мама.
Введем переменные для простых
высказываний:
М = «Мама поедет на дачу»;
Р = «Папа поедет на дачу»; D =
«Дочь поедет на дачу»;
— «Собака поедет на дачу» .
Приведенные высказывания запишем в алгебраической форме. Из фразы «Если мама поедет на дачу, то поедет и папа» следует, что если на дачу едет мама, то папа поедет обязательно. В то же время возможно, что папа поедет на дачу, а мама нет. Поэтому здесь нужно применить операцию следования, в которой посылкой является высказывание «Мама поедет на дачу», а заключением «Папа поедет на дачу»: М —» Р.
Второму высказыванию «Дочь поедет на дачу тогда и только тогда, когда поедут мама, папа и собака» соответствует логическая операция эквивалентности: D (М & Р & S). Эти два события взаимообусловлены: если едет дочь, то едут мама, папа и собака; и наоборот: если едут мама, папа и собака, то едет и дочь. То есть имеем необходимое и достаточное условие.
Третье высказывание «Собака поедет на дачу только тогда, когда поедет дочь или мама» означает: если поехала собака, то, значит, поехала мама или дочь. Здесь имеет место необходимое условие: для того чтобы поехала собака, необходима поездка мамы или дочери. Но это условие не является достаточным: если поедут мама или дочь, то собаку они могут взять с собой, а могут и не взять. Значит, здесь должна использоваться операция следования, в которой посылкой является высказывание «Собака поедет на дачу», а заключением: «Дочь поедет на дачу или мама поедет на дачу»: S (D v М).
Перепишем еще раз все три высказывания в алгебраической форме:
|
Логические основы обработки информации |
|
 |
(логические величины)
В языках программирования
существует логический тип данных. В Паскале переменные логического типа
описываются в разделе описания переменных с помощью ключевого слова Ьоо1еап.
Логические константы задаются словами true истина, fa1se 
ложь.
В Паскале имеются четыре логические операции: отрицание (not), конъюнкция (and), дизъюнкция (or) и исключающее «или» (xor).
Следующая программа выводит на экран компьютера таблицу истинности четырех логических операций.
Program Logtab1; Var А, В: Ьоо1еап; begin
Write1n( А 
пое А 
' А and
А or в т
А xor В ' ) ; for A:=fa1se Ео true
do for B:=fa1se to true do
Write1n (А: 7, В: 7, пое А.
А xor в: 7) епа .
Результаты работы программы отразятся на экране в следующем виде:
|
|
В |
пое А А and В А or В А xor В |
|
FALSE |
FALSE |
TRUE FALSE FALSE FALSE |
|
FALSE |
TRUE |
TRUE FALSE ТМЕ ТЕШЕ |
|
TRUE |
FALSE |
FALSE FALSE TRUE TRUE |
|
TRUE |
TRUE |
FALSE TRUE TRUE FALSE |
|
|
Теоретические основы информатики |
|
110 |
 |
Логический тип данных — это множество, состоящее из двух величин, расположенных в следующем порядке: false, true. false является предыдущим по отношению к true, а true является последующим по отношению к false. Между ними истинно отношение: false true. Это связано и с их внутренним представлением в компьютере. Двоичный код false — О, двоичный код true — 1. Хотя информацию несет всего лишь 1 бит, но в памяти логическая величина занимает 1 байт. Следовательно, семь остальных битов такого байта являются неинформативными.
Заголовок оператора цикла: for A:=fa1se Ео true do определяет изменение в цикле значения логической переменной А от false до true. Два вложенных цикла по переменным А и В организуют перебор всех сочетаний значений этих величин. Всего их четыре.
Система основных понятий
|
Логика и логические операции |
|
|
Формальная логика |
Алгебра логики |
|
Наука о формах правильного мышления. Возникла в IV в. до н. э. Аристотель |
Математический аппарат логики, математическая логика. Возникла в XIX в. Д. Буль, О. де Морган, П. С. Порецкий, А. А. Марков и др. |
|
Объекты изучения: высказывания; истинность и ложность высказываний; законы логики |
Объекты изучения: логические величины (истина, ложь), логические константы и переменные, логические операции; законы алгебры логики |
|
Логические операции |
|
|
Отрицание — НЕ |
НЕ истина ложь, НЕ ложь истина |
|
Логическое умножение (конъюнкция) — И |
истина И истина = истина. Иначе ложь |
|
Логическое сложение (дизъюнкция) — ИЛИ |
ложь ИЛИ ложь ложь. Иначе истина |
|
Исключающее ИЛИ |
Истина тогда и только тогда, когда операнды имеют разные значения |
|
Следование (импликация) |
ЕСЛИ истина, ТО ложь = ложь. Иначе истина |
|
Эквивалентность |
Истина тогда и только тогда, когда операнды имеют одинаковые значения |
Вопросы и задания
1. Что является предметом изучения в логике Аристотеля?
2. Обоснуйте название дисциплины «алгебра логики».
З. Приведите примеры высказываний на бытовые темы, в которых используются шесть логических операций. Запишите в символической форме, используя символику алгебры логики, придуманные вами высказывания.
4. Определите значение истинности следующих высказываний:
а) Приставка есть часть слова, И она пишется со словом раздельно;
б) Суффикс есть часть слова, И он стоит после корня;
в) Рыбу ловят сачком, ИЛИ ловят крючком, ИЛИ мухой приманивают ИЛИ червяком;
г) Две прямые на плоскости параллельны ИЛИ пересекаются.
5.
 |
а) Если утром тучи в небе, то к обеду будет дождь;
б) Если Костя — брат N, то лт — брат Кости;
в) Если Х — сын или дочь У, то У — мать или отец Х;
г) Людоед голоден тогда и только тогда, когда он давно не ел.
Практикум. Раздел З «Логика»
В алгебре чисел существует понятие алгебраического выражения. Вот пример алгебраического выражения: (а + b)2 . Аналогом этого понятия в алгебре логики является понятие логического выражения (логической формулы). Логическая формула может включать логические константы, логические переменные, знаки
логических операций. Для влияния на последовательность выполнения операций в логических формулах могут использоваться скобки. Пример логической формулы: (А & В) —» (А & С).
|
|
Теоретические основы информатики |
 |
Логической функцией называется зависимость значения одной переменной логической величины (значения функции) от значений других независимых логических величин аргументов. Способ вычисления логической функции описывается логической формулой. Например:
F(A, В, С) = (А 8, В) (А С).
— функция от трех логических аргументов
А, В, С. Перебором всех вариантов значений аргументов можно определить все
соответствующие значения функции. Это делается путем построения таблицы
истинности логической функции. Если функция имеет лт аргументов, то
при этом приходится перебирать 2N вариантов значений аргументов. В
нашем примере лт = З, значит таблица истинности (в ней «истина» и
«ложь» обозначены как 1 и О) функции F содержит 8 строк:
|
А |
в |
|
|
|
|
|
|
о |
о |
о |
1 |
о |
о |
1 |
|
о |
о |
1 |
1 |
о |
1 |
1 |
|
о |
1 |
о |
1 |
о |
о |
1 |
|
о |
1 |
1 |
1 |
о |
1 |
1 |
|
1 |
о |
о |
о |
о |
о |
1 |
|
|
о |
1 |
о |
о |
о |
1 |
|
1 |
1 |
о |
о |
1 |
|
|
|
1 |
1 |
1 |
о |
1 |
|
|
Логическая формула путем тождественных преобразований может быть приведена к другому виду (об этом — далее). И только таблица истинности является однозначным отображением логической функции.
Законы алгебры логики
Вспомним рассмотренный в предыдущем параграфе пример двух равносильных высказываний: 1) «Квадратное уравнение имеет действительные корни тогда и только тогда, когда его дискриминант положительный»; 2) «Если квадратное уравнение имеет действительные корни, то его дискриминант положительный» И «Если дискриминант квадратного уравнения положительный, то оно имеет действительные корни».
Приведенный пример демонстрирует, что операция
эквивалентности А В равносильна (тождественна) одновременному выполнению двух
операций импликации: А В и В А. Данное утверждение можно записать в виде
равенства между двумя логическими формулами:
(1)
 |
Тождественность обозначает, что при любых значениях переменных а и Ь равенство будет выполняться. Это равенство между двумя алгебраическими выражениями. Тождественные преобразования не отражаются на значениях алгебраических выражений, а изменяют лишь их форму. Чтобы правильно выполнять тождественные преобразования, нужно знать законы алгебры.
Соотношение (1) является тождеством двух логических формул. Каким способом можно вывести или доказать справедливость равенства между двумя логическими формулами? Наиболее простой способ для этого: построение таблиц истинности для обеих формул. И если значения формул в таблицах полностью совпадают, то это значит, что эти формулы тождественны. Докажем таким путем справедливость следующего равенства:
|
|
|
|
|
|
|
и |
и |
л |
и |
и |
|
и |
л |
л |
л |
л |
|
л |
и |
и |
и |
и |
|
л |
л |
и |
и |
и |
Значения формул полностью совпали, значит, формулы тождественны, что и требовалось доказать.
А теперь вернемся к соотношению (1). Применяя к его правой части равенство (2), получим:
(3)
Полученное равенство (З) — это выражение закона алгебры
логики, сводящего операцию эквивалентности к последовательности операций
отрицания, дизъюнкции и конъюнкции.
|
|
Теоретические основы информатики |
 |
Такой способ представления логической формулы называется нормальной формой.
Приведем список основных законов (тождеств) алгебры логики.
В таблице 1.12 логическая константа «ложь» обозначена как О, а «истина» — как
1.
Таблица 1.12
Законы алгебры логики
|
|
Законы ком ативности |
||
|
1 |
|
||
|
2 |
AvB=BvA |
||
|
|
Законы ассоциативности |
||
|
з |
|
||
|
4 |
|
||
|
|
Законы дис иб ивности |
||
|
5 |
|
||
|
6 |
(АМВ |
||
|
|
Закон идемпотентности |
||
|
7 8 |
|
||
|
Законы поглощения нуля и единицы 9 |
|
|||
|
|
|
|
||
|
10 Закон исключенного третьего |
|
|||
|
11 |
|
|
||
|
12 |
|
|
||
|
Законы поглощения |
|
|||
|
13 |
|
|
||
|
14 |
|
|
||
|
Законы де Моргана |
|
|||
|
15 |
|
|
||
|
16 |
|
|
||
|
Закон двойного отрицания |
|
|||
|
17 |
|
|
||
|
Приведение к нормальной форме |
|
|||
|
18 |
В = А мв |
|
||
|
19 |
нВ = (А ч.? В) 8, (В мА) |
|
||
|
20 |
ЭВ— (А В) (А |
|
||
Вернемся к рассмотрению примера «Шахматы» из предыдущего пункта.
Пример, Шахматы (продолжение)
Поскольку все три высказывания истинны одновременно, их можно объединить в одно сложное высказывание (логическую формулу) путем применения операции конъюнкции. Учитывая закон коммутативности для конъюнкции, запишем:
(4)
|
Логические основы обработки информации |
|
|
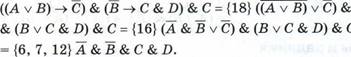(5)
|
|
Теоретические основы информатики |
 |
|
Логические формулы и функции |
||
|
Логическая формула |
Логическая функция |
Таблица ИСТинносТИ логической функции |
|
Выражение, содержащее логические константы, логические переменные, знаки логических операций |
Зависимость значения одной переменной логической величины от других независимых логических величинаргументов |
Перечень значений функции для всех сочетаний значений аргументов. Содержит 2 71 строк, где п — число аргументов |
|
Законы алгебры логики |
||
|
Законы коммутативности |
|
|
|
Законы ассоциативности |
|
|
|
Законы дистрибутивности |
|
|
|
Законы идемпотентности |
|
|
|
Законы поглощения нуля и единицы |
|
|
|
Законы исключенного третьего |
|
|
|
Законы поглощения |
|
|
|
Законы де Моргана |
|
|
|
Закон двойного отрицания |
|
|
|
Теорема о нормальной форме |
||
|
Любую логическую формулу путем тождественных преобразований можно привести к формуле, содержащей только операции отрицания, дизъюнкции и конъюнкции. |
||
|
Приведение к нормальной форме |
||
|
|
|
|
О Вопросы и задания
1. Что такое логическая формула? Какие значения получаются в результате вычисления логической формулы?
2. Какую из двух следующих формул можно рассматривать в качестве логической функции?
1) -(ИСТИНА & ЛОЖЬ); 2) -(ИСТИНА А).
З. Если сопоставить операции логического сложения и логического умножения операциям сложения и умножения чисел, а операцию логического отрицания операции изменения знака числа (унарный минус), то какие законы алгебры логики имеют аналоги в алгебре чисел?
Замечание: далее следуют задания тестового типа с выбором ответа из данного меню.
4. Для какого из указанных значений Х истинно высказывание
5. Укажите, какое логическое выражение равносильно выражению
6. Символом F обозначена логическая функция от трех логических аргументов: Х, У, Z. Дан фрагмент таблицы истинности функции Е:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
Какая формула соответствует Е?
|
Логические основы обработки информации |
|
7.
|
(К ж., L) (L & М & У) = ЛОЖЬ, где К, L, М, лг — логические переменные? (Указать количество различных наборов значений переменных К, L, М, N, удовлетворяющих уравнению.)
1) 4; 2) 10; 3) 8; 4) 12.
Практикум. Раздел З «Логика»
Логические схемы в наглядной
графической форме отображают последовательность выполнения операций при
вычислении логических формул. Основные логические операции будем изображать на
таких схемах в форме, показанной в табл. 1.13.
Входящие слева линии и цифры около них обозначают значения операндов, линия справа и соответствующая цифра — результат операции (значения на выходах логических элементов). Здесь 1 логическая единица (истина), О логический ноль (ложь).
В таблице 1.13 фактически представлены таблицы истинности, только в форме логических схем. В такой форме удобно изображать цепочки логических операций и производить их вычисле-
Таблица 1.13
Схематическое изображение логических операций
|
Конъюнкция |
Дизъюнкция |
Отрицание |
|||||||||||||||
|
|
|
|
|
|
Теоретические основы информатики |
 |
1 или о и 1 нарисуем схему, отражающую последовательность выполнения логических операций:
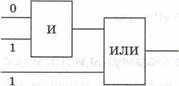
Читать эту схему надо слева направо. Здесь
наглядно отражено то, что первой выполняется операция И, затем ИЛИ. Теперь в
порядке слева направо припишем к выходящим линиям результаты операций:
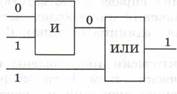
В результате получилась 1, т. е. «истина».
Пример 2. Представим в форме логической схемы следующую логическую формулу:
НЕ (А И ( В ИЛИ С) И 0),
где А, В, С, D — логические переменные. Логическая схема будет выглядеть так:
|
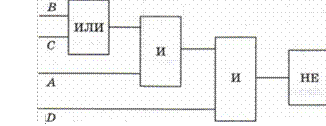
Логические основы обработки информации |
|
 |
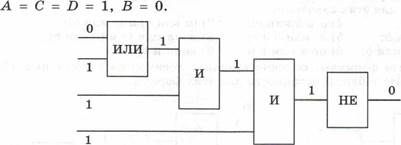
В результате получился логический ноль, т. е, «ложь».
Использованные нами обозначения логических элементов не соответствуют стандартам, принятым в компьютерной схемотехнике. Согласно существующим стандартам, для элементов логических схем используются следующие обозначения:
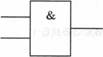Элемент «И» (конъюнктор)
|
|
1 |
|
|
|
|
|
Элемент «ИЛИ» (дизъюнктор)
С использованием стандартных обозначений для логических элементов схема из примера 2 будет выглядеть так:
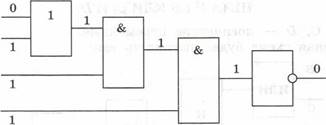
Вопросы и задания
О 1. Пусть а, Ь, с — логические переменные, которые имеют следующие значения: а = истина, Ь = ложь, с = истина. Используя логические схемы, определить результаты вычисления следующих логических формул для этих значений:
4)
а и Ь или с; 7) (а или Ь) и (с или Ь);
2) а или Ь; 5) а или Ь и с; 8) не (а или Ь) и (с или Ь); З) не а или Ь; 6) не а или Ь и с; 9) не (а и Ь и с).
|
|
Теоретические основы информатики |
|
2. Запишите формулы,
соответствующие логическим схемам а) и б). Постройте таблицы истинности для
этих формул.
а)б)
|
|
|
||||||||||||||||||||
1.6.4. Методы решения логических задач
Метод рассуждений
Продемонстрируем применение метода рассуждений на примере задачи о шахматистах. Повторим условие задачи.
О Пример 1, Шахматы
Есть четыре друга: Антон, Виктор, Семён и Дмитрий. Относительно их умения играть в шахматы справедливы следующие
1) Семён играет в шахматы;
2) если Виктор не играет в шахматы, то играют Семён и Дмитрий;
З) если Антон или Виктор играет, то Семён не играет.
Требуется узнать, кто играет в шахматы, а кто нет.
Эту задачу можно решить, ничего не зная про алгебру логики, но обладая бытовыми навыками логического мышления.
В задаче уже есть одно простое высказывание (1), содержащее часть ответа. «Зацепившись» за него, можно из других сложных высказываний последовательно «вытащить» оставшиеся части решения. Рассуждения можно построить так.
Поскольку Семён играет в шахматы, из 3-го утверждения следует, что ни Антон, ни Виктор в шахматы не играют. Осталось выяснить вопрос о Дмитрии. Мы выяснили, что Виктор в шахматы не играет, значит, из 2-го утверждения следует, что Семён и Дмитрий играют в шахматы. Про Семёна было уже известно, что он играет, теперь мы узнали, что и Дмитрий играет в шахматы. Задача имеет единственное решение.
|
|
121 |
 |
Пример 2. Поездка на дачу
В семье есть мама, папа, дочь и собака. Справедливы следу-
ЮЩИе высказывания:
1) если мама поедет на дачу, то поедет и папа;
2) дочь поедет на дачу тогда и только тогда, когда поедут мама, папа и собака;
З) собака поедет на дачу только тогда, когда поедет дочь или мама.
Требуется определить все варианты групп из членов семьи, которые могут поехать на дачу. В отличие от задачи про шахматистов здесь нет единственного решения.
Задача решается методом гипотез. Гипотеза это предположение об истинности некоторого дополнительного высказывания, уменьшающее, таким образом, степень неопределенности ответа. Если гипотеза не приведет к противоречию ни одного из данных высказываний, то она верна. Если нет, то следует принять другую гипотезу.
Делается предположение о том, что кто-то из членов семьи поедет на дачу. Затем по данным высказываниям выясняется, что из этого следует. Истинными должны быть все три высказывания одновременно!
Ответим на вопросы.
1. Кто еще поедет на дачу, если поедет дочь?
Из 2-го высказывания следует, что в таком случае на дачу поедут все остальные. При этом будут истинны 1-е и 3-е высказывания.
2. Кто еще поедет на дачу, если поедет собака?
В этом случае всем трем условиям удовлетворит только один вариант: поедут все.
З. Кто еще поедет на дачу, если поедет папа?
Возможны следующие варианты: 1) поедет один папа, т. е. больше никто; 2) поедут папа и мама; З) поедут все.
4. Кто еще поедет на дачу, если поедет мама?
Гипотеза приводит к уже рассмотренным вариантам: либо поедут все, либо поедут мама и папа. Еще нужно учесть случай, когда на дачу не поедет никто. Следовательно, задача имеет четыре варианта ответа.
О Пример З, Турнир четырех
Перед началом Турнира четырех болельщики высказали следующие предположения по поводу своих кумиров:
1) Макс победит, Билл будет вторым;
|
122 |
|
|
Теоретические основы информатики |
2)
 |
З) Макс будет последним, а первым — Джон.
Когда соревнования закончились, оказалось, что кажДый из
болельщиков был прав ровно в одном из своих прогнозов. Какие места на турнире
заняли Джон, Ник, Билл и Макс?
Эта задача имеет однозначное решение. Поскольку в условии нет готовой части ответа (как в задаче про шахматистов), то решать ее нужно методом гипотез.
1-я гипотеза: Макс — первый. Из 1-го
высказывания следует, что Билл не второй, т. е. Билл третий или четвертый. Из
2-го 
высказывания следует, что если Билл
четвертый, то Ник— первый, чего быть не может. Если же Билл — третий, то Ник 
второй
или четвертый. Из 3-го высказывания, с учетом того что Макс первый, следует
противоречие: Джон и Макс одновременно первые. Следовательно, принятая гипотеза
неверна.
2-я гипотеза, учитывающая результат проверки 1-й гипотезы:
Макс не первый. Из 1-го высказывания следует, что Билл — второй. Из 2-го
высказывания следует, что Ник — первый. Из 3-го высказывания следует, что Макс
четвертый (так как Джон не первый), а Джон третий (что осталось). Все сошлось!
Значит, места распределились в таком порядке: 1-е 
Ник, 2-е — Билл, 3-е —
Джон, 4-е — Макс.
Использование табличных моделей
Как хорошо известно, пониманию человеком сложных ситуаций помогает применение наглядных моделей, делающих исследуемую ситуацию обозримой. Для решения логических задач эффективным приемом является использование табличных моделей. Рассмотрим следующий пример.
Пример 4, Три друга и собаки
Три друга — Алёша,
Серёжа и Денис — купили щенков разной породы — колли, ротвейлера и овчарку.
Дали им клички 
Джек, Гриф и Шарик. Известно, что:
1) щенок Алёши темнее по окрасу, чем овчарка, Шарик и Джек; 2) щенок Серёжи старше Джека, ротвейлера и овчарки.
Определить, щенок с какой кличкой и какой породы какому мальчику принадлежит.
Построим две таблицы: табл. 1.14, отражающую ОТНОШение (связь) между именами мальчиков и кличками щенков, и табл. 1.15, показывающую отношение между именами мальчиков и породами щенков.
|
|
123 |
 |
Таблица 1.15 заполняется аналогично. Рассуждения описывать не будем. Выполните их самостоятельно. Окончательный вывод следующий: у Алёши — ротвейлер Гриф, у Серёжи колли Шарик, у Дениса — овчарка Джек.
Таблица 1.14 Таблица 1.15
|
|
|
В таблицах 1.14 и 1.15 вместо плюсов и минусов можно писать соответственно ИСТИНА и ЛОЖЬ или единицы и нули. Такого рода таблицы, в ячейки которых заносятся двоичные значения, называются двоичными матрицами.
Заметим, что применение аппарата алгебры логики для этой простой задачи значительно усложнило бы ее решение. Во-первых, нужно было бы обозначить символами все возможные простые высказывания:
А — «У Алёши Джек»;
В — «У Серёжи Джек»;
С «У Дениса Джек»;
D — «У Алёши Гриф»;
К = «У Алёши колли»;
L — «У Серёжи колли»;
Затем написать конъюнкцию двух логических формул, описывающих 1-е и 2-е высказывания. После этого выполнить упрощение полученной формулы и построить ее таблицу истинности, из которой сделать выводы об истинности или ложности исходных простых высказываний.
Построение и упрощение логических формул
 |
Логическая формула, которая получается при решении задачи «Поездка на дачу», поддается следующему тождественному преобразованию (промежуточные преобразования не показаны):
Такой вид логической формулы называется совершенной дизъюнктивной нормальной формой — СДНФ. СДНФ — последовательность операций дизъюнкции, объединяющих между собой элементарные конъюнкции, которые содержат одинаковое число одних и тех же переменных или их отрицаний. Хотя формула выглядит длинной, ее смысл легко понять. Значение формулы будет истинным, если будет выполнено хотя бы одно из следующих условий:
1) Р, М, D, S — одновременно принимают значение ЛОЖЬ (никто не поедет на дачу);
2) Р — ИСТИНА, а все остальные — ЛОЖЬ (поедет на дачу толь-
З) Р, М — ИСТИНА, остальные — ЛОЖЬ (поедут папа и мама);
4) Р, М, 1), S — одновременно принимают значение ИСТИНА (все поедут на дачу).
Заметим, что в рассмотренной СДНФ скобки можно было не писать, учитывая приоритеты логических операций: логическое умножение старше логического сложения. Скобки сохранены для большей наглядности формулы.
Учимся программировать
(решение логических задач)
С увеличением числа «персонажей» и количества и сложности высказываний всё более затруднительным для человека становится метод рассуждений даже с применением табличного моделирования. Можно ли в таком случае прибегнуть к помощи компьютера? Конечно, можно! Однако надо понимать, что компьютер решает формализованные задачи, формализация выполняется на языке системы команд компьютера.
|
|
125 |
|
Логические основы обработки информации |
|
Из предыдущего параграфа на примере Паскаля вы узнали, что в языках программирования используются величины логического типа и существуют логические операции. Если человек хочет применить программирование для решения логической задачи, он сначала должен ее формализовать, т. е. построить логические формулы по правилам алгебры логики.
Всякую логическую формулу можно рассматривать как реализацию логической функции от многих логических переменных: F(X1, хи...,хп). Компьютер сам не может выполнить ее преобразование в более простую форму, используя законы алгебры логики. Например, если в формулу входят операции следования и эквивалентности, которых нет в языке программирования, то программисту самому придется выполнить приведение этой формулы к нормальной форме. Но после этого совсем не обязательно пытаться упростить нормализованную формулу, чтобы сократить число операций в ней. Ведь считать придется не вам, а компьютеру!
Благодаря способности компьютера к быстрым вычислениям, на нем возможно решение многих задач методом прямого перебора всех вариантов. Если анализируемая логическая функция содержит п логических аргументов, то число всех вариантов при полном переборе равно 2 '1 . В результате такого перебора можно получить таблицу истинности данной логической функции. Далее программист может либо сам просмотреть ее и выбрать интересующие его варианты, либо такой просмотр и отбор предусмотреть в программе. Если большое значение, то лучше анализ полученных результатов поручить компьютеру.
О Пример 5, Поездка на дачу (продолжение)
В семье есть мама, папа, дочь и собака. Если мама поедет на дачу, то поедет и папа. Дочь поедет на дачу тогда и только тогда, когда поедут мама, папа и собака. Собака поедет на дачу, только тогда, когда поедет дочь или мама.
Формализуем задачу. Введем обозначения для простых высказываний:
М = «Мама поедет на дачу»;
Р = «Папа поедет на дачу»; D = «Дочь поедет на дачу»;
S = «Собака поедет на дачу».
Приведенные высказывания запишем в алгебраической форме:
|
|
Теоретические основы информатики |
|
Полученную формулу упрощать не будем. Составим программу, вычисляющую все значения логической функции от четырех аргументов:
Program Dacha;
Var Р, М, г, S , Е: boolean; begin
Write1n( Р 
for P:=fa1se €0 true do for 
to true do for D:=fa1se to true do
for S 
Ео true do begin
(пое М or Р) and( (пое D or(M and Р
and S ) ) and (not(M and Р and S ) or D) ) and (пое S or
end
|
Логические основы обработки информации |
|
|
на 1.
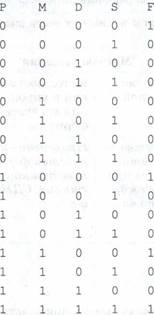
Анализируя таблицу, видим, что возможны четыре ситуации: 1) никто не поедет на дачу; 2) один папа поедет; З) поедут папа с мамой; 4) все поедут на дачу. Эти же выводы мы получали методом рассуждений. Благодаря составленной программе, компьютер тоже смог решить эту задачу.
Можно было выводить не всю таблицу истинности, а только те ее строки, которые соответствуют значению true величины Е. Для этого достаточно оператор вывода поместить в условный оператор следующего вида:
if then 
М: 7, D:7, S:7, Е: 7) ;
|
128 |
|
|
Теоретические основы информатики |
 |
|
Методы решения логических задач |
|||
|
Логическая задача: поиск истинных высказываний в ответ на поставленный вопрос |
|||
|
Методы решения |
|||
|
Метод рассуждений |
Метод построения табличной модели |
Метод построения и упрощения логической формулы |
Программирование метода перебора |
|
Цепочка ВЫВОДОВ от частного решения. МетоД гипотез |
Преимущество — в нагляДноспш. Двоичная матрица: связи мелсДу Двумя типами оббењтов |
Приведение к простой форме: простая КОНбюнкция, СДНФ и пр. |
Автоматическое получение таблицы истинности логической функции. Вложенные циклы по логическим параме трам |
Вопросы и задания
1. Для решения каких задач можно применять метод рассуждений?
2. Что такое метод гипотез?
3. В чем суть метода табличного моделирования?
Указание: для решения последующих задач подберите подходящий метод решения (рассуждений или табличного моделирования) и решите задачи.
О 4. На столе лежат три пачки тетрадей 5-го, 7-го и 10-го классов. На первой пачке написано: «10 класс», на второй «5 или 7 класс», на третьей — «7 класс». Известно, что ни одна надпись не верна. В какой пачке лежат тетради 5-го класса?
О 5. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке. Сосуд с лимонадом находится между кувшином и сосудом с квасом. В банке — не лимонад и не вода. Стакан находится между банкой и сосудом с молоком. Как распределены жидкости по сосудам?
6. Определите, кто из подозреваемых участвовал в преступлении, если
известно, что:
1) если Иванов не участвовал или Петров участвовал, то Сидоров
участвовал;
2) если Иванов не участвовал, то Сидоров не участвовал.
7. В нарушении правил обмена валюты подозреваются четыре работника банка: А, В, С и Г). Известно, что:
1) если А нарушил, то и В нарушил правила обмена валюты;
2) если В нарушил, то С нарушил или А не нарушил; З) если D не нарушил, то А нарушил, а С не нарушил;
4) если D нарушил, то и А нарушил.
Кто из подозреваемых нарушил правила обмена валюты? Задачу решите путем построения и преобразования логической формулы.
Практикум. Раздел З «Логика»
1 .6.5. Логические функции на области числовых значений
Алгебра чисел пересекается с алгеброй логики в тех случаях, когда приходится проверять принадлежность значений алгебраических выражений некоторому множеству. Например, принадлежность значений числовой переменной Х множеству положительных чисел выражается через высказывание: «Х больше нуля». Символически это записывается так: Х > О. В алгебре такое выражение называют неравенством. В логике отношением.
|
Логические основы обработки информации |
|
 |
<выражение 1> <знак отношения> «(выражение 2>
Здесь выражения 1 и 2 некоторые математические
выражения, принимающие числовые значения. В частном случае выражение может
представлять собой одну константу или одну переменную величину. Знаки отношений
могут быть следующими: 
равно 
не равно
2 больше или равно S меньше или равно
> больше меньше Например:
х = 5; а + Ь * х— 1; 6 2 — 4ас 20; sinx<
Итак, отношение это простое высказывание, а значит,
логическая величина. Оно может быть как постоянной величиной: 
— всегда
ИСТИНА, З * 6:2 — всегда ЛОЖЬ; так и переменной: а Ь, х + 1 = с — d.
Отношение можно рассматривать как логическую функцию от
числовых аргументов. Например: F(x) — (х > О) или Р(х, у)
(х < у). Аргументы определены на
бесконечном множестве действительных чисел, а значения функции на множестве,
состоящем из двух логических величин: ИСТИНА, ЛОЖЬ.
Логические функции от числовых аргументов еще называют термином «предикат». В алгоритмах предикаты играют роль условий, по которым строятся ветвления и циклы. Предикаты могут быть как простыми логическими функциями, не содержащими логических операций, так и сложными, содержащими логические операции.
О Пример 1. Записать предикат (логическую функцию) от двух вещественных аргументов х и у, который будет принимать значение ИСТИНА, если точка с координатами х и у на координатной плоскости лежит внутри единичной окружности с центром в начале координат (рис. 1.22).
|
|
Теоретические основы информатики |
|
|
|
||
|
|
х |
1 |
|
 |
Рис. 1.22
Из геометрических соображений понятно, что для всех точек, лежащих внутри единичной окружности, будет истинным значение следующей логической функции:
F(x, у) = (х2 + у2 < 1).
Для значений координат точек, лежащих на окружности и вне ее, значения функции F будет ложным.
О Пример 2. Записать предикат, который будет принимать значение ИСТИНА, если точка с координатами х и у на координатной плоскости лежит внутри кольца с центром в начале координат и радиусами r1 и r2.
Поскольку значения r1 и r2 — переменные величины, искомая логическая функция будет иметь четыре аргумента: х, у, r1, r2. Возможны две ситуации:
1) r1 е: х2 + у2 r2 и r1 < r2: r1 — внутренний радиус, r2 — внеш-
ний радиус;
2) r2 < х2 + у2 < r1 и r2 < r1: r2 — внутренний радиус, r1 — внеш-
ний радиус.
Объединив дизъюнкцией оба этих утверждения и записав их по правилам алгебры логики, получим следующую логическую функцию:
F(x, у, r1, r2) = (((х2 + у 2 ) > r1 2) & ((х2 + у2) < r2 2) & r1 < r2) v
(((x2 + у2 ) > r2
2) & ((х2 + у2 ) < r1 2 )
& r2 < r1).
|
Логические оснОвы обработки информации |
|
|
|
131 |
Пример З, Записать предикат, который будет принимать значение ИСТИНА, если точка с координатами х и у на координатной плоскости лежит внутри фигуры, ограниченной голубыми линиями на рис. 1.23.
|
|
1 |
|
|
|
|
-1 |
1 |
Рис. 1.23
|
Фигура ниями: |
ограничена тремя границами, описываемыми уравне- |
|
|
— левая граница, линейная функция; |
|
2 у = х |
— правая граница, парабола, |
Рассматриваемая область есть пересечение трех полуплоскостей, описываемых неравенствами:
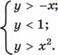
Во внутренних точках области все эти три отношения являются одновременно истинными. Поэтому искомый предикат имеет вид:
F(x, у) = (у > —х) & (х < 1) & (у > х 2 ).
Учимся программировать
(использование датчика случайных чисел)
Составим программу на Паскале, по которой будет приближенно вычислена площадь фигуры, изображенной на рис. 1.23. Метод, с помощью которого будем решать эту задачу, называется методом статистических испытаний, или методом Монте-Карло.
Рассмотрим прямоугольник со сторонами, описываемыми уравнениями: у = О, х —1, у = 1, х = 1. Этот прямоугольник содержит внутри себя исследуемую нами область. Площадь прямоугольника равна 2.
Последовательно случайным образом выбираются точки, лежащие внутри прямоугольника. Делается это так, чтобы при большом числе точек они были равномерно разбросаны по прямоугольнику. В теории вероятностей это называется законом равномерного распределения вероятности по области значений. Для этой цели в Паскале существует стандартная функция, которая называется Датчиком случайных чисел.
|
|
Теоретические основы информатики |
|
132 |
 |
ры. К точному значению площади эта величина будет стремиться при N, стремящемся к бесконечности.
Следующая программа на Паскале реализует применение метода Монте-Карло для вычисления фигуры, представленной на рис. 1.23.
Program Monte kar10;
Var х, у, S : rea1;
N, т, i: 10ngint; begin
Write Read1n (Ы) ; Ввод числа ИСпЫТаниЙ} randomi ze ; { Случайное начальное состояние датчика)
€0
do Цикл повторения ИСПЫТаНИЙ} beg in
Вычисление случайных
координат точки} х : —2 * random— 1 ; У : =random;
{ Предикат попадания внутрь фигуры У
if ( (у>—х) and (у<1) and (у>х*х) ) then т : 1 Подсчет числа попаданий} end;
{
Вычисление площади 
S) (Вывод результата} end.
Проведем три вычислительных эксперимента, последовательно увеличивая число испытаний. В результате будут получены следующие значения:
|
1) 100000 |
— вводимая величина; |
|
S 1,16738 |
— вычисленная площадь. |
|
2) 1000000 |
— вводимая величина; |
|
S = 1,16662 |
— вычисленная площадь. |
|
3) тут = 10000000 |
— вводимая величина; |
|
S = 1,1666186 |
— вычисленная площадь. |
С точностью до 10-4 , площадь фигуры равна 1,1666.
|
Логические основы обработки информации |
|
 |
Получение случайного значения обеспечивает функция
random. Она может записываться без аргумента (без скобок). В таком случае
результат этой функции вещественное число в полуинтервале [О, 1). Такие
значения в нашей программе принимает переменная у. Переменная х вычисляется
оператором x:=2*random—1. 
Ее значения будут принадлежать
полуинтервалу [—1, 1), что и требуется по условию задачи.
randomize это стандартная процедура, которая устанавливает случайное начальное состояние функции random. Тогда при каждом новом запуске программы функция random будет генерировать другие случайные последовательности чисел.
Для правильной записи сложного логического выражения (предиката) нужно учитывать относительные приоритеты (старшинство) арифметических, логических операций и операций отношений, поскольку все они могут присутствовать в логическом выражении. По убыванию приоритетов операции располагаются в следующем порядке:
1. Арифметические операции:
— (минус унарный)
2. Логические операции:
not and or, xor
З. Операции отношения:
Обратите внимание, что в логическом выражении в операторе if ( (у>-х) and (у<1) and (у>х*х) )
операции отношения заключены в скобки, поскольку они «младше» логических операций, а выполняться должны раньше.
|
|
Теоретические основы информатики |
 |
|
Логические функции на области числовых значений |
|
|
Отношения между величинами: |
математические неравенства; результат вычисления — логическая величина |
|
Предикат:
|
логическая функция, содержащая числовые аргументы и операции отношения; определяет принадлежность значений аргументов некоторому множеству |
|
Датчик случайных чисел: |
стандартная функция в языке программирования, вычисляющая случайные значения числа в некотором ограниченном интервале, в соответствии с некоторым законом распределения вероятности |
|
Функция random в Паскале: |
возвращает случайное число из полуинтервала [О, 1) с равномерным законом распределения вероятности |
Вопросы и задания
1. Величина какого типа получается при вычислении отношения (неравенства) между числами?
2. Что такое предикат? Приведите примеры.
3.
Запишите на языке
алгебры логики логические функции, которые будут принимать значение ИСТИНА,
если справедливы следующие утверждения, и ЛОЖЬ — в противном случае:
а) все числа х, у, г равны между собой;
б) из чисел х, у, г только два равны между собой; 
в) каждое из чисел х, у, z положительно;
г) только одно из чисел х, у, положительно;
д) значения чисел х, у, упорядочены по возрастанию.
4. Все формулы, полученные при решении предыдущей задачи, запишите в виде логических выражений на Паскале.
5. Вычислите значения следующих логических выражений, записанных на Паскале:
а) К mod К div 5 —1 при К = 15;
б) odd (trunc (10*Р) ) при Р = 0,182;
в) пое odd (п) при п = О;
г) and (Р mod з = 0) при true, Р = 10101;
д) (х * у о О) and (у > х) при х
= 2, у = 1; 
or пое Ь при а = false, Ь = true.
Пояснения: odd (х) — логическая функция определения четности аргумента. Равна true, если х — нечетное, и равна false, если х — четное. trunc (х) — целая функция от вещественного аргумента, возвращающая ближайшее целое число, не превышающее х по модулю.
Практикум. Раздел 5 «Программирование»
|
Алгоритмы обработки информации |
|
 |
Определение и свойства алгоритма
В этом разделе снова вернемся к теме алгоритмов, но обсудим ее более детально. Кратко повторим то, что рассказывалось про алгоритмы в курсе информатики 7—9 классов.
Алгоритм понятное и точное
предписание исполнителю выполнить конечную последовательность действий,
приводящих от исходных данных к искомому результату.
Ключевое понятие в этом определении — исполнитель алгоритмов. В параграфе 1.5.4 понятие «исполнитель алгоритмов» было использовано как синоним понятия «исполнитель обработки информации». Здесь и в дальнейшем мы будем говорить только об алгоритмах обработки информации, не принимая в расчет другие трактовки понятия «алгоритм» (например, алгоритмы работы светофора или стиральной машины). Договоримся также о том, что будем рассматривать только программно управляемых исполнителей — алгоритмические машины.
|
Пример нарушения понятности В программе на Паскале записан оператор: — 4*а*с; Программист имел в виду, что значок обозначает возведение в степень. Но такой операции (команды) в Паскале нет. Программа не может быть выполнена. |
Возможности исполнителя определяются его системой команд 
СКИ
(Система Команд Исполнителя). Это конечное множество команд-инструкций, которые
исполнитель понимает, т. е. умеет выполнять. Свойство понятности алгоритма
состоит в том, что в алгоритме должны использоваться только команды из СКИ.
|
Иллюстрация дискретности Фрагмент алгоритма: х:=1; х : 4+1 ;
Каждая следующая команда использует результат выполнения предыдущей команды, поэтому может быть выполнена только после её завершения. |
Другое свойство
алгоритма 
дискретность означает, что каждая
команда алгоритма должна выполняться отдельно от других: выполнение должно
начаться после окончания предыдущей команды и закончиться до начала выполнения
следующей команды.
|
|
Теоретические основы информатики |
Заметим, что данная формулировка дискретности подразумевает использование однопроцессорного исполнителя. Этот вопрос подробнее будет обсуждаться в разделе, посвященном архитектуре компьютера и многопроцессорным вычислительным системам. Скажем только, что в многопроцессорных системах происходит распараллеливание выполнения алгоритма, когда несколько команд могут выполняться одновременно разными процессорами.
Будем различать понятия «команда алгоритма» и «шаг» или «действие» исполнителя. Шаг — это действие, предпринимаемое исполнителем по команде алгоритма. Если алгоритм содержит циклы, то число шагов при его выполнении может быть ббльшим, чем число команд. А за счет выполнения ветвлений число шагов может оказаться меньшим, чем число команд.
Свойство конечности алгоритма заключено в данном выше определении: результат должен быть получен за конечное число шагов выполнения алгоритма. Это свойство называют также результативностью.
Свойство точности алгоритма означает, что каждая команда должна определять однозначное действие исполнителя, не требуя ных» решений. Например, если команда содержит числовой параметр, то значение этого параметра должно быть определено до выполнения этой команды.
Если алгоритм обладает всеми названными свойствами, то его исполнение будет происходить формально, что необходимо для создания автоматического исполнителя алгоритмической машины.
Свойства понятности, дискретности, конечности, точности являются необходимыми для любого алгоритма. Однако часто к ним добавляют еще одно свойство массовость. Массовость означает то, что алгоритм должен быть предназначен для решения не одной частной задачи, а некоторого класса задач. Например, алгоритм должен решать не только квадратное уравнение: 3х2 — 5х + 1 = О, но и любые квадратные уравнения вида ах2 + bx + с = О.
Свойство массовости не является необходимым свойством алгоритма, оно определяет его качество. Безусловно, алгоритм, реплЮЩИЙ любое квадратное уравнение, лучше, полезнее, чем тот, что решает одно конкретное уравнение. Но от этого последний не перестает быть алгоритмом. Он лишь не обладает свойством массовости.
|
Алгоритмы обработки информации |
|
 |
Выполнение универсального алгоритма всегда должно заверШ&гЬСЯ путем, предусмотренным программой. Возможные ошибки во время исполнения должны диагностироваться программой, и сообщения о них должны выводиться на экран. Алгоритм решения квадратного уравнения ах2 + bx + с = О должен правильно реагировать на любые значения а, Ь, с и в любом случае что-то выводить: либо корни уравнения, либо сообщение о невозможности вычисления корней. Построение такого алгоритма требует предварительного математического исследования решаемой задачи.
Способы описания алгоритмов
Существуют различные способы описания алгоритмов. В курсе информатики 7—9 классов вы познакомились с блок-схемами алгоритмов и с учебным Алгоритмическим языком (АЯ). Однако блок-схема или алгоритм на АЯ не являются программами для компьютера. Это лишь модели программы, которые строятся до ее составления. Чаще всего они используются в учебных целях. А опытные программисты пишут сразу программу на языке программирования. Существуют разные языки программирования, реализующие разные способы программирования.
В 1960-х годах возникает и развивается структурная методика программирования, основанная на положении о том, что любой алгоритм обработки информации можно построить, используя три алгоритмические структуры: следование, ветвление, цикл. Ориентированные на структурную методику программирования алгоритмы, записанные в форме блок-схем и на АЯ, также должны изображаться по определенным правилам, позволяющим наглядно отобразить структуру алгоритма. Основное правило для блок-схем: стандартное изображение отдельных блоков и базовых алгоритмических структур. В алгоритмах на АЯ следует соблюдать сдвиги строк для наглядного отображения структуры алгоритма так же, как это принято делать в структурных языках программирования.
|
|
Теоретические основы информатики |
 |
В таблице 1.16 приведены примеры описания различных алгоритмических структур на языке блок-схем, на учебном Алгоритмическом языке и на языке программирования Паскаль.
В алгоритмах на АЯ использованы сокращения: нц — начало цикла, кц конец цикла, кв конец ветвления. Для иллюстрации циклических структур используется задача вычисления факториала целого положительного числа.
Обратите внимание на
то, что для блок-схем и АЯ нет строгих правил для записи математических
выражений или расстановки точек с запятой. В то же время в Паскале все правила
синтаксиса строго соблюдаются.
Более подробное знакомство со структурным программированием, с языками и технологиями программирования у вас состоится позже, в разделе, посвященном программированию (учебник для 11 класса). Тем не менее во всех примерах программ, которые в нашем учебнике приводились раньше, строго соблюдались принципы структурного программирования. Так мы будем поступать и дальше.
|
|
139 |
|
|
Язык блок-схем |
Учебный Алгоритмический язык |
Язык программирования Паскаль |
||||||
|
Следование |
|
|||||||
|
|
Ввод а, Ь, с d: =b 2 —4ac |
Read1n (а, Ь, с) ;
|
||||||
|
Ветвление |
|
|||||||
|
|
' Нет корнеи |
if d>=0 then begin (d) )
епа else Write1n Нет корней!) |
||||||
|
|
икл с предусловием |
|
||||||
|
|
|
к:=1 пока kSN повторять
|
whi1e k<=N do begin
К:=К+1 end ; |
|||||
|
|
|
kSN |
||||||
|
F:-F.k |
|
|
||||||
|
|
||||||||
|
|
|
|||||||
|
Цикл с постусловием |
|
|||||||
|
|
к:=1 повторять
до k>N |
repeat
until k>N ; |
||||||
|
|
икл с па |
амет |
ом |
|
||||
|
|
|
|
||||||
|
|
Теоретические основы информатики |
 |
|
Определение, свойства, описание алгоритма |
|||
|
Алгоритм — понятное и точное преДписание исполнителю выполнить конечную послеДовательность Действий, привоДящих от исходных Данных к искомому результату |
|||
|
Система команд исполнителя (СКИ): конечное множество инструкций, которые исполнитель умеет выполнять |
|||
|
Свойства алгоритма |
|||
|
Понятность |
Дискретность |
Конечность |
Точность |
|
В алгоритме используются только команДы из ски |
КажДый шаг алгоритма выполняется отДельно от Других |
Результат получается за конечное число шагов выполнения алгоритма |
КажДая команДа опреДеляет однозначное Действие исполнителя |
|
Массовость алгоритма: алгоритм преДназначен Для решения класса заДач |
|||
|
Универсальность алгоритма по отношению к исходным данным: при любых значениях исходных Данных алгоритм Должен правильно выполняться ц не Должен аварийно завершать свое выполнение |
|||
|
Языки описания алгоритмов |
|||
|
Язык блоксхем |
Учебный Алгоритмический язык |
Языки программирования |
|
|
Графическое отображение алгоритма |
Структурное описание с русскими служебными словами |
Системы описанця программ Для выполнения на компьютере |
|
Вопросы и задания
1. Что такое система команд исполнителя?
2. Определите систему команд для автоматического кассового аппарата в магазине.
З. Как вы думаете, справедливо ли утверждение «Синтаксический
контроль транслятором текста программы предназначен для проверки соблюдения свойства понятности алгоритма». Приведите примеры, подтверждающие или опровергающие это утверждение.
4. В чем разница между понятиями «команда алгоритма» и «шаг выполнения алгоритма»? Приведите примеры, когда не совпадает число команд и число шагов.
5. Приведите пример алгоритма, в котором нарушено свойство конечности (отличный от примера в тексте параграфа).
6. Дан алгоритм: Х •.=1; У •.=5; Х:=2*Х; У:=У—1. Все ли команды этого алгоритма обязательно должны выполняться дискретно-последовательным способом? Можно ли производить выполнение каких-то команд в один и тот же промежуток времени?
7. Для программ Russian method и АШ Horezmi из параграфа 1.5.4 «Обработка информации» опишите алгоритмы на языке блок-схем и на учебном Алгоритмическом языке.
8. Постройте алгоритм решения следующей задачи. Дано два числа: а и Ь.
а
Вычислить: с = Алгоритм должен обладать свойством универ-
сальности по отношению к исходным данным. Запишите алгоритм на языке блок-схем, на АЯ и на Паскале.
1 .7.2. Алгоритмическая машина Тьюринга
В 30-х годах ХХ века
возникает новая наука теория алгоритмов. Вопрос, на который искала ответ эта
наука: для всякой ли задачи обработки информации может быть построен алгоритм
решения? Но, чтобы ответить на этот вопрос, надо было договориться об
исполнителе, на которого должен быть ориентирован алгоритм.
|
Алгоритмы обработки информации |
|
|
|
141 |
Английский ученый Алан Тьюринг предложил модель такого исполнителя, получившую название «машина Тьюринга». По мысли Тьюринга, его «машина» является универсальным исполнителем обработки лю-
|
бых символьных последовательностей в лю- |
Алан Тьюринг |
|
бом алфавите. |
(1912-1954) |
Устройство машины Тьюринга
Машина Тьюринга обрабатывает символьные послеДовательности слова. Всё множество символов образует внешний алфавит машины. Символы записываются в позиции (ячейки) на бесконечной ленте — памяти машины. На рисунке 1.24 приведен пример слова, записанного на ленту. Использован алфавит десятичной системы счисления.
Рис. 1.24. Модель машины Тьюринга
В общем виде символы алфавита будем обозначать так: ао, Ч, ..., а п. Самый первый символ ао это пустой символ,
или пробел. Считается, что во всех пустых ячейках расположен символ ао.
Другой составляющей машины Тьюринга является автомат: программно управляемое считывающее/записывающее устройство. На рисунке 1.24 головка автомата обозначена треугольником. Головка автомата установлена на определенной (текущей) ячейке и под управлением программы может считывать и записывать символы в текущую ячейку, а также перемещаться влево или вправо к соседним ячейкам.
Автомат может находиться в разных состояниях. Таких состояниЙ конечное множество. Будем их обозначать: qo, (11 , , и называть внутренним алфавитом машины.
Программирование машины Тьюринга
Машина Тьюринга предназначена для решения следующего класса задач: на ленте записано некоторое входное слово. Нужно получить выходное слово, которое будет результатом решения задачи. В такой постановке можно рассматривать любую задачу обработки данных. Например:
|
|
Теоретические основы информатики |
1)
 |
2) увеличить число на единицу: входное слово — «327», выходное слово — «328»;
З) сложить два числа: входное слово — «25 + 37», выходное слово — «25 + 37 = 62».
Входное слово — слово на ленте, ограниченное пустыми
ячейками, на одном из символов которого установлена головка автомата,
находящегося в начальном состоянии (10. Выходное слово 
слово, остающееся на
ленте после остановки работы автомата, головка которого установилась на одном
из символов, Ситуация, при которой автомат никогда не останавливается,
называется зацикливанием. При построении машины Тьюринга нельзя допускать
зацикливания.
Для решения каждого типа задач строится
своя машина Тьюринга, которая представляется в табличном виде (табл. 1.17).
Строки озаглавлены символами внешнего алфавита, а столбцы 
символами
внутреннего алфавита (состояниями автомата). Программа управления работой
машины Тьюринга записывается в виде команд, помещенных в ячейки таблицы.
Таблица с занесенными в ее ячейки командами управления называется
функциональной схемой машины Тьюринга.
Команда программы имеет такую структуру:
Здесь:
символ, заносимый в
текущую ячейку; 
направление смещения головки; 
следующее
состояние автомата.
Таблица 1.17
Таблица для программирования машины Тьюринга
|
|
|
|
|
|
|
|
|
ао |
|
|
|
|
|
|
|
01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Направление смещения может обозначаться одним из двух символов:
Смещение вправо; 
влево.
|
Алгоритмы обработки информации |
|
 |
Начальное состояние всегда обозначается как (10. Если автомат находился в состоянии qj напротив ячейки с символом а! (табл.
1.17), то по команде ак qp в эту ячейку занесется символ ак, автомат перейдет в состояние (1 и головка сместится вправо.
Задача 1. Дано целое число в троичной системе счисления.
Нужно увеличить его на единицу. Примеры решения задачи:
|
|
ходное слово |
ыходное слово |
||||
|
|
з |
|
|
з |
||
|
|
|
з |
|
з |
||
|
|
з |
|
03 |
|||
|
з |
|
|
з |
|||
Внешний алфавит этой задачи следующий: пробел, О, 1, 2.
Состояние автомата всегда одно: (10. Головка автомата расположена на ячейке с
младшим разрядом числа (как показано на рис. 1.24). Программа для машины
Тьюринга представлена в следующей функциональной схеме:
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
Если в младшем разряде стоит О или 1, то цифра увеличивается на 1 и работа заканчивается. Если в младшем разряде двойка, то она заменится на ноль и произойдет смещение головки влево. Дальше повторяется предыдущий алгоритм. Если все цифры — двойки, то они заменятся на нули и на месте первого слева пробела появится единица.
Задача 2. Условие задачи то же, что у задачи 1. Но начальное положение головки автомата может быть на любом символе исходного слова.
Решение задачи разбивается на два этапа:
1) подвести головку автомата к
младшему разряду числа; 2) прибавить к числу единицу (как в задаче 1).
Выполнение первого этапа происходит в состоянии (10, выполнение второго этапа в состоянии (11. Программа решения задачи:
|
|
|
|
||||
|
ао |
ао е— (11 |
|
(71 |
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Теоретические основы информатики |
 |
Эту задачу можно решить путем двукратного применения программы из задачи 2. Здесь в состоянии (10 происходит установка головки автомата на младший разряд; в состоянии q1 — прибавление единицы к числу; в состоянии (12 — возврат головки к младшему разряду; в состоянии (13 — повторное прибавление единицы. Функциональная схема машины Тьюринга, решающей эту задачу:
|
|
|
|
(11 |
|
|
(13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(10 |
|
о |
(12 |
|
|
|
|
|
1 |
(10 |
2 Э (12 |
|
|
2 (13 ! |
|
2 |
|
|
|
|
|
|
|
Машина Тьюринга обрабатывает символьные последовательности, которые хранятся в ее памяти на бесконечной ленте, разделенной на бесконечное число ячеек. Поскольку у реальной машины не может быть бесконечной памяти, машина Тьюринга это всего лишь идеальная конструкция.
Главная идея автора состояла в том, чтобы уточнить понятие алгоритма, решить проблему алгоритмической разрешимости задачи. Ответ на вопрос об алгоритмической разрешимости задачи по Тьюрингу звучит так.
Алгоритмически разрешима та задача, для решения которой можно построить машину Тьюринга.
А на вопрос «Что такое алгоритм решения задачи?» ответ следующий.
Алгоритм это программа Для машины Тьюринга, привоДящая к решению поставленной заДачи.
|
|
145 |
 |
|
Алгоритмическая машина Тьюринга |
||
|
Машина Тьюринга — модель универсального исполнителя алгоритмов обработки символьных последовательностей |
||
|
Устройство машины Тьюринга |
||
|
Информационная лен- та (память машины) |
Автомат для чтения/записи символов |
|
|
Бесконечная линейная последовательность ячеек |
Устройство для считывания/записи символов в ячейки, способное перемещаться вдоль ленты и менять свое состояние |
|
|
Функциональная схема (программа) |
||
|
Внешний алфавит |
Внутренний ал авит |
КоманДа программы |
|
Множество символов для представления информации: ао, 01, п |
Множество состояний автомата:
|
— символ, заносимый в текущую ячейку; е — направление смещения головки; ъ— следующее состояние автомата |
|
Алгоритмически разрешима та задача, для решения которой можно построить машину Тьюринга |
||
Вопросы и задания
1. Какую основную задачу решает теория алгоритмов?
2. В чем состоит назначение машины Тьюринга?
З. Как по Тьюрингу звучит определение
алгоритмической разрешимости задачи?
4. Можно ли физически реализовать машину Тьюринга? Какое ограничение приходится вносить в устройство машины Тьюринга при создании ее программной модели?
5. Проанализируйте применительно к программам для машины Тьюринга выполнение основных свойств алгоритма: дискретности, понятности, точности, конечности, массовости. Подготовьте сообщение.
Практикум. Раздел 4 «Теория алгоритмов»
О 1 .7.3. Алгоритмическая машина Поста
Практически
одновременно с Тьюрингом (в 1936—1937 годах) другую модель алгоритмической
машины описал Эмиль Пост. Машина Поста работает с двоичным алфавитом и
несколько проще в своем «устройстве». Можно сказать, что машина Поста является
частным случаем машины Тьюринга. Однако именно работа с двоичным алфавитом
представляет наибольший интерес, поскольку Эмиль Пост современный компьютер
тоже работает с дво(1897-1954) ичным алфавитом.
Устройство машины Поста
Как и в машине Тьюринга, в машине Поста имеется бесконечная информационная лента, разделенная на позиции ячейки (рис. 1.25). В каждой ячейке может либо стоять метка (некоторый знак), либо отсутствовать метка.
|
|
Теоретические основы информатики |
Вдоль ленты движется головка автомата. На рисунке 1.25 она обозначена треугольником. Головка может передвигаться шагами: один шаг — смещение на одну ячейку вправо или влево. Ячейку, на которой установлена головка автомата, будем называть текущей.
Рис. 1.25. Модель машины Поста
Автомат
может выполнять следующие действия: 
распознать, пустая ячейка или содержит
метку; 
стереть метку в текущей ячейке; 
поставить
метку в пустую текущую ячейку.
Если произвести замену меток на единицы, а пустых клеток 
на нули,
то информацию на ленте можно будет рассматривать как аналог данных в памяти
компьютера. Существенное отличие автомата машины Поста от процессора компьютера
состоит в том, что в компьютере возможен доступ процессора к ячейкам памяти в
произвольном порядке, а в машине Поста только последовательно.
Назначение машины Поста — производить любые преобразования на информационной ленте. Исходное состояние ленты можно рассматривать как исходные данные задачи, конечное состояние
ленты как результат решения задачи. Кроме того, в исходные данные входит информация о начальном положении головки автомата.
Программирование машины Поста
Рассмотрим систему команд машины
Поста, приведенную в табл. 1.18. Запись любой команды начинается с ее
порядкового номера в программе п. Затем следует код операции и после него —
номер следующей выполняемой команды программы
Таблица 1.18
|
Алгоритмы обработки информации |
|
 |
|
Команда |
Действие |
|
|
|
двиг головки автомата на шаг влево и переход к выполнению команды с номером т |
|
|
|
двиг головки на шаг вправо и переход к выполнению команды с номером т |
|
|
|
апись метки в текущую пустую ячеику и переход к выполнению команды с номером т |
|
|
п т |
тирание метки в текущеи яче ке и переход к выполнению команды с номером т |
|
|
|
|
становка выполнения программы |
|
п т, |
ереход по содержимому текущеи ячеики: если текущая ячейка пустая, то следующей будет выполняться команда с номером т, если с меткой, то выполнится команда номер К |
|
Задача 1, Рассмотрим пример программы решения задачи на машине Поста. Исходная обстановка показана на рис. 1.25. Имеется группа подряд расположенных меток. В удаленной ячейке слева от них имеется метка, на которой установлена головка автомата. Машина должна стереть метку в текущей ячейке и присоединить ее к группе меток, расположенных справа от головки. Задача решается по следующей программе:
|
Команда |
Действие |
|
|
1 t 2 |
Ст ание метки; переход к следующей команде |
|
|
3? 2, 4 |
Сдвиг вправо на один шаг Если ячейка пустая, то переход к команде 2, иначе — к команде 4 |
|
|
|
двиг влево на шаг команда выполнится, когда головка вы дет на первую метку группы) |
|
|
|
|
апись метки в пустую яче ку |
|
|
становка машины |
|
В процессе выполнения приведенной программы многократно повторяется выполнение команд с номерами 2 и З. Это цикл.
Напомним, что цикл относится к числу основных алгоритмических структур вместе со следованием и ветвлением.
Задача 2, Теперь научим машину Поста играть в интеллектуО альную игру, которая называется «Игра Баше». Опишем правила
игры.
Играют двое. Перед ними 21 (или 16, или 11 и т. д., т. е. всего 5п + 1) фишек. Игроки берут фишки по очереди. За один ход можно взять от 1 до 4 фишек. Проигрывает тот, кто забирает последнюю фишку.
Имеется выигрышная тактика для игрока, берущего фишки вторым. Она заключается в том, чтобы брать такое количество фишек, которое дополняет число фишек, взятых соперником на предыдущем ходе, до пяти штук.
|
|
Теоретические основы информатики |
 |
|
Команда |
Действие |
|
1 |
Машина ждет появления пустой ячейки над кареткой. После хода человека машина вступит в игру. Если человек видит всего одну метку на ленте, он прекращает игру, признав свое поражение |
|
З |
Эта серия команд выведет головку автомата на пятую позицию. Какой бы ход ни сделал соперник, в ней обязательно будет стоять метка |
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
Стирание метки в текущей ячейке |
|
8 |
Шаг влево |
|
6 |
Если ячейка не пустая, то возврат к команде 6 |
|
10 |
Перемещение на шаг вправо |
|
10 ? |
Если ячейка не пустая, то возврат к команде 1 и ожидание хода партнера (человека) или признания им своего поражения |
Действуя по данной программе и начиная стирать метки второй после человека, машина всегда будет выигрывать, если правильно задано начальное число меток, которое должно быть равно 5п + 1, где п любое натуральное число. В противном случае машина может проиграть.
В теории алгоритмов было доказано, что алгоритмические модели машин Тьюринга и Поста являются эквивалентными
с точки зрения решения проблемы алгоритмической разрешимости задачи. Это значит, что любая алгоритмически разрешимая задача может быть решена путем программирования как для машины Тьюринга, так и для машины Поста.
Нормальные алгоритмы Маркова
 |
Значительный вклад в теорию алгоритмов внес российский математик
Андрей Андреевич Марков (младший). Его подход отличается от «машинного» подхода
Тьюринга и Поста, в которых фигурируют понятия «лента памяти» , «ячейки» ,
«состояние машины» , « считывание» и т. д. В нормальном алгоритме Маркова
используется понятие подстановки одних
|
символов на место других. Алгоритм опреде- |
Андрей Андреевич |
|
ляет, какие замены (подстановки) символов в |
Марков (младший) (1903-1979) |
исходном слове надо производить и в каком порядке это делать.
Доказано, что если задача является алгоритмически разрешимой,
т. е. она может быть решена с помощью машин Тьюринга и Поста, 
то для нее
можно построить и нормальный алгоритм Маркова.
Система основных понятий
|
Алгоритмическая машина Поста |
|
|
Машина Поста — модель универсального исполнителя алгоритмов обработки символьных последовательностей |
|
|
Отличие от машины Тьюринга |
В ячейки заносится один символ — метка. Содержимое памяти — двоичный код, если принять метки за единицы, а пустые ячейки — за нули |
|
|
Исполнительный автомат имеет только одно состояние |
|
Программа |
Последовательность пронумерованных команд |
|
|
Система команд:
|
|
Нормальные алгоритмы Маркова |
Описание допустимых подстановок символов и последовательности их выполнения |
|
Теорема об эквивалентности алгоритмических моделей |
Любая алгоритмически разрешимая задача моЖет быть решена путем программирования как для машины Тьюринга, так и для машины Поста |
1. В чем смысл эквивалентности алгоритмических машин Тьюринга и Поста и нормальных алгоритмов Маркова?
2. На информационной ленте машины Поста отмечен массив из 2 2 меток. Головка автомата находится на крайней левой метке. Какая обстановка установится на ленте после выполнения следующей программы?
|
1 |
|
2 23 |
|
|
|
4 ? 5 2 |
|
5 |
|
6 |
|
7! |
Практикум. Раздел 4 «Теория алгоритмов»
 |
Компьютер — исполнитель алгоритмов
Алгоритмическим решением задачи будем называть способ решения путем программирования некоторого автоматического исполнителя. Автоматические исполнители, рассмотренные в предыдущих параграфах, — машины Тьюринга и Поста — реально не существуют. Они являются лишь теоретическими моделями, позволяющими решать проблему алгоритмической разрешимости задачи.
Реально существующим универсальным автоматическим исполнителем обработки информации является компьютер. Программа управления компьютером это алгоритм решения задачи, представленный на языке машинных команд или на языке программирования. Система команд, на основе которой строится алгоритм, определяется правилами используемого языка программирования.
Для большинства современных языков программирования процедурного типа в систему команд исполнителя входят следующие основные команды (операторы): ввод, вывод, присваивание, ветвление, цикл. Первые две команды можно назвать простыми командами, две последние — структурными.
В дальнейшем, составляя алгоритмы, мы будем ориентироваться на эту систему команд. В качестве языка программирования по-прежнему будем использовать Паскаль.
Этапы решения задачи
Постановка задачи и формализация
Словом «задача» называют проблему, которая требует решения. Решение задачи начинается с ее постановки. На этапе постановки заДачи в терминах предметной области (физики, экономики, биологии и др.) определяются исходные данные и результаты, которые надо получить.
Следующий этап — формализация заДачи. Чаще всего процесс формализации означает перевод задачи на язык математики: формул, уравнений, неравенств, систем уравнений, систем неравенств и т. п.
 |
Анализ математической задачи
Решение полученной математической задачи требует знания математики, умения выполнять анализ математической задачи. Такой анализ необходим для того, чтобы построить правильный алгоритм решения, обладающий всеми свойствами алгоритма, сформулированными в предыдущем параграфе.
Пусть в результате формализации некоторой задачи было получено квадратное уравнение: ах2 + bx + с = О, где коэффициенты а, Ь, с являются исходными данными. Требуется решить это уравнение, т. е. найти его корни. Проведем анализ этой математической задачи.
Рассмотрим различные варианты значений исходных данных, которые приводят к разным результатам для решающего ее алгоритма. Ограничимся поиском только вещественных корней уравнения. Проанализируем все возможные варианты множества значений коэффициентов а, Ь, с.
|
Если а = О, Ь = О, с = О, |
то любое х — решение уравнения |
|
|
Если а = О, Ь = О, с О, |
то уравнение решений не имеет |
|
|
Если а = О, Ь О, |
то это линейное уравнение, которое имеет одно решение: х = —c/b |
|
|
Если а |
О и d = b2 — 4ас О, |
то уравнение имеет два вещественных корня:
|
|
Если а |
О и d < О, |
то уравнение не имеет вещественных корней |
Построение алгоритма
|
|
Теоретические основы информатики |
 |
задачи. Здесь вместо
слов «да» и «нет» использованы знаки «+»
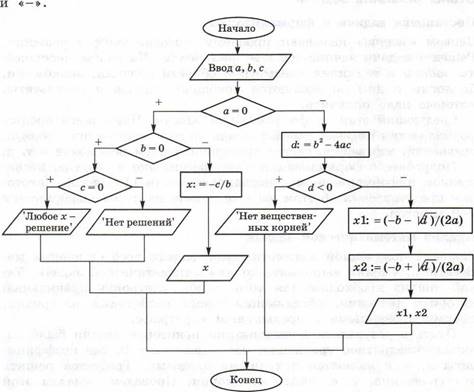
Рис. 1-26. Блок-схема алгоритма решения квадратного уравнения
Построенный алгоритм, несомненно, удовлетворяет свойству универсальности по отношению к исходным данным. Запишем этот же алгоритм на учебном Алгоритмическом языке. алг корни квадратного уравнения вещ а, Ь, с, d, х 1, х2 нач ввод а, Ь, с
иначе
—c/b вывод х
иначе
d: =b 2 —4ac
если то вывод ” Нет вещественных корней“
иначе
/ (2а)
кон
В этом алгоритме многократно использована структурная команда ветвления. Общий вид команды ветвления в блок-схемах и на алгоритмическом языке следующий:
|
|
153 |
|
если условие то серия 1 иначе серия 2
Если на ветвях одного ветвления содержатся другие ветвления, то такой алгоритм имеет структуру вложенных ветвлений. Именно такую структуру имеет алгоритм корни квадратного уравне— ния. Обратите внимание на смещения строк в тексте алгоритма. При этом соблюдается принцип: запись всякой вложенной структуры должна быть смещена на несколько позиций вправо относительно записи внешней структуры. Конструкции одного уровня вложенности записываются на одном вертикальном уровне.
Программирование
После того как записан алгоритм на учебном Алгоритмическом языке, составление программы на языке программирования становится несложной задачей. Рассмотрим программирование на Паскале. Основное внимание следует уделять строгому соблюдению синтаксических правил языка. Правило смещения строк в тексте программы то же, что было сформулировано выше для Алгоритмического языка. Соответствующие друг другу служебные слова begin и end должны располагаться друг под другом.
Program Roots ;
Var а, Ь, с, d, х1, х2: rea1; begin
WriteLn ( ' Введите коэффициенты
квадратного уравнения :
Write( ; ReadLn (а) ; Write ( ReadLn (Ь) ; Write( с= ReadLn (с) ;
then
then if 
then WriteLn ( ' Любое
х — решение ) else WriteLn ( Нет решений ' ) e1se begin x:=—c/b;
|
|
Теоретические основы информатики |
 |
then WriteLn ( Нет
вещественных корней ' ) e1se begin
(—b+sqrt (d)
) / 2 / а; х2 : = (—b—sqrt (d) ) / 2 / а; WriteLn ( х
WriteLn ( ' end end
Чем больше текст программы, тем больше вероятность совершения ошибок при ее записи и вводе в компьютер. Ошибки, нарушающие правила грамматики языка, называются синтаксическими ошибками. Поиск и устранение синтаксических ошибок в программе называются отладкой. Отладить программу программисту помогает система программирования на данном языке, которая автоматически обнаруживает ошибки и сообщаег о них программисту. Подробнее о системах программирования вы узнаете из раздела, посвященного программированию (в 11 классе).
Тестирование программы
Тестирование это этап, на котором экспериментально исследуется правильность алгоритма, реализованного в программе, с помощью некоторого набора тестов. Выявляются присутствующие в программе ошибки. Тест это вариант решения задачи с заданными исходными данными, для которых известен результат.
Предварительно должен быть составлен план тестирования. Для ветвящегося алгоритма должны быть протестированы все ветви алгоритма. В нашем примере пять ветвей, пять вариантов ответа. Значит, в плане тестирования должно быть не менее пяти вариантов теста.
В таблице 1.19 представлен план тестирования программы
Roots и результаты проведенного тестирования,
Таблица 1.19
|
Алгоритмы обработки информации |
|
 |
|
|
Исходные значения |
Верные результаты |
Результаты тестирования |
|
1 |
|
Любое х — решение |
Любое х — решение |
|
2 |
|
Нет решений |
Нет решений |
|
З |
|
|
х=З |
|
4 |
|
|
х1=1 х2=-1 . 5 |
|
5 |
|
Нет вещественных корней |
Нет вещественных корней |
Теперь, анализируя результаты тестирования, делаем вывод: правильность алгоритма и работоспособность программы проверены.
Если какой-то из вариантов теста не дает ожидаемого результата, значит, в программе есть ошибки. Например, пусть программист ошибочно записал следующие операторы присваивания для вычисления корней:
х 1 (—b+sqrt (d) ) / 2 * а; х2 (—b—sqrt (d) ) /2*а;
Результаты всех тестов, кроме 4-го, совпали с ожидаемыми, а в 4-м тесте получилось: х1 = 4, х2 —6. После этого программист обратит внимание на выражения для вычисления корней и исправит ошибки: либо заменит знак умножения на знак деления, либо заключит в скобки выражение 2*а.
|
|
Теоретические основы информатики |
О Система основных понятий
|
Этапы алгоритмического решения задачи |
|
|
Постановка задачи |
Определение исходных данных и искомых результатов (в терминах предметной области) |
|
Формализация |
Представление задачи в некоторой знаковой системе. Например, в виде математической задачи |
|
Анализ математической задачи |
Определение всех вариантов множеств значений исходных данных. Определение для каждого варианта способа решения и вида выходных данных (результаТОВ) |
|
Построение алгоритма |
Определение структуры алгоритма, последовательности команд. Представление на каком-либо языке описания алгоритмов (блок-схемы, учебный Алгоритмический язык) |
|
Составление программы |
Запись и отладка программы на языке программирования. Строгое соблюдение правил синтаксиса языка |
|
Тестирование |
Экспериментальное доказатедьство правильности алгоритма и работоспособности программы. Тест — вариант решения задачи с заданными исходными данными, для которых известен результат. План тестирования строится так, чтобы наиболее полно проверить работу программы |
О Вопросы и задания
Сформулируйте основные цели этапов алгоритмического решения задачи.
Практикум. Раздел 5 «Программирование»
1 .7.5. Алгоритмы поиска данных
Вспомните, как часто приходится вам
искать какие-нибудь данные. Таких примеров много и в бытовых ситуациях, и в
учебном процессе. Например, в программе телепередач вы ищете время начала
трансляции футбольного матча; в расписании поездов 
сведения о поезде,
идущем до нужной вам станции. На уроке физики, решая задачу, ищете в таблице
удельный вес меди. На уроке английского языка, читая иностранный текст, ищете в
словаре перевод слова на русский язык. При работе на компьютере вам нередко
приходится искать на его дисках нужные файлы или производить поиск в Интернете
интересующих вас сведений.
Постановка задачи поиска данных
При выполнении любого поиска данных имеются три составляющие поиска.
Первая составляющая поиска: набор данных. Это вся совоКупность данных, среди которых осуществляется поиск. Элементы набора данных будем называть записями. Запись может состоять из одного или нескольких полей. Например, запись в записной книжке состоит из полей: фамилия, адрес, телефон.
Вторая составляющая поиска: ключ поиска. Это то поле записи, по значению которого происходит поиск. Например, поле «Фамилия», если мы ищем номер телефона определенного человека.
|
Алгоритмы обработки информации |
|
 |
Заметим, что ключей поиска может быть несколько, ' тогда и критерий поиска будет составным, учитывающим значения сразу нескольких ключей. Например, если в справочнике имеется несколько записей с фамилией Сидоров, но у них разные имена, а вам нужен Сидоров Владимир, то составной критерий поиска будет включать два условия: фамилия — Сидоров, имя — Владимир.
Как при «ручном» поиске, так и при автоматизированном важнейшей задачей является сокращение времени поиска. Оно зависит от двух обстоятельств от того:
1) как организован набор данных в информационном хранилище
(в словаре, в справочнике, на дисках компьютера и пр.);
2) каким алгоритмом поиска пользуется человек или компьютер.
Организация набора данных
Относительно первого пункта могут быть две ситуации: либо данные никак не организованы, либо данные структурированы.
Под словами «данные структурированы» понимается наличие упорядоченности данных в их хранилище: в словаре, в расписании, в компьютерной базе данных.
Структурированные системы данных, хранящиеся на каких-
О либо носителях, будем называть структурами данных.
Однако бывает и так, что хранимая информация не систематизирована. Представьте себе, что вы записывали адреса и телефоны своих знакомых в записную книжку без алфавитного инДењса («лесенки» из букв по краям листов). Записи велись в порядке поступления, а не в алфавитном порядке. А теперь вам нужно найти телефон определенного человека. Что остается делать? Просматривать всю книжку подряд, пока не попадется нужная запись! Хорошо, если повезет и запись окажется в начале книжки. А если в конце? И тут вы поймете, что книжка с алфавитом гораздо удобнее.
Последовательный поиск
|
|
Теоретические основы информатики |
 |
Опишем алгоритм поиска методом последовательного перебора. Для описания алгоритма используем язык блок-схем (рис. 1.27). В алгоритме учтем два возможных варианта результата: искомые сведения найдены и сведения не наидены. Результаты поиска нередко оказываются отрицательными, если в наборе нет искомых данных.
Из блок-схемы видно, что если искомый элемент найден, то поиск может закончиться до окончания просмотра всего набора данных. Если же элемент не обнаружен, то поиск закончится только после просмотра всего набора данных.
Зададимся вопросом: какое среднее число просмотров приходится выполнять при использовании метода последовательного перебора? Есть два крайних частных случая:
1) искомый элемент оказался первым среди просматриваемых. Тогда просмотр всего один;
2) искомый элемент оказался последним в порядке перебора. Тогда количество просмотров равно N, где лт — размер набора данных. То же будет, если элемент вообще не найден.
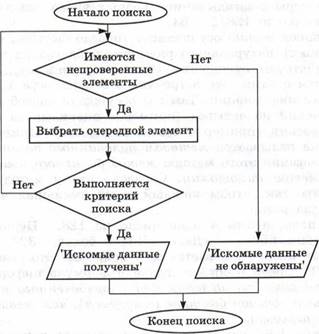Нет
|
Алгоритмы обработки информации |
|
|
|
159 |
Рис. 1 .27. Алгоритм поиска последовательным перебором
Всякие средние величины принято определять по большому числу проведенных опытов. На этом принципе основана целая наука под названием математическая статистика. Нетрудно понять, что если число опытов (поисков) будет очень большим, то среднее число просмотров во всех этих опытах окажется приблизительно равным N/2. Эта величина определяет длительность поиска — главную характеристику процесса поиска.
Поиск половинным делением
В качестве примера поиска рассмотрим игру в угадывание целого числа в определенном диапазоне, например от 1 до 128. Один играющий загадал число, второй пытается его угадать, задавая вопросы, на которые ответом может быть только «да» или «нет». Это задача поиска, в которой набором Данных является множество натуральных чисел от 1 до 128, ключом поиска значения чисел, а критерием поиска совпадение значения задуманного игроком числа с одним из чисел набора данных.
Если вопросы задавать такие: «Число равно единице?» (Ответ: «Нет»), «Число равно двум?» и т. д., то это будет последовательный перебор. Среднее количество вопросов при многократном повторении игры с загадыванием разных чисел из данного диапазона будет равно 128/2 = 64.
Однако поиск можно осуществить гораздо быстрее, если учесть упорядоченность натурального ряда чисел, благодаря чему между числами действуют отношения «больше» / «меньше». С подобной ситуацией мы с вами уже встречались в параграфе 1.2.2, говоря об измерении информации. Там мы обсуждали способ угадывания одного значения из четырех (пример с оценками за экзамен) и одного из восьми (пример с вагонами поезда). Применявшийся метод поиска называется методом половинного Деления. Другие варианты названия этого метода: метоД бинарного поиска, метоД бисекций, метоД Дихотомии. Согласно этому методу, вопросы надо задавать так, чтобы каждый ответ уменьшал число неизвестных в два раза.
Так же надо искать и одно число из 128. Первый вопрос: «Число меньше 65?» «Да.». «Число больше 32?» « Нет. » и т. д. Любое число угадывается за 7 вопросов. Это связано с тем, что 128 2 7. Снова работает главная формула информатики.
Метод половинного Деления для упорядоченного набора данных работает гораздо быстрее (в среднем), чем метод послеДовательного перебора.
|
|
Теоретические основы информатики |
|
оророооо
0000 1-й вопрос
офо 2-й вопрос
Ф) 3-й вопрос
Рис. 1 .28. Выполнение поиска половинным делением
Если максимальное число диапазона лг не равно целой степени двойки, то оптимальное количество вопросов не будет постоянной величиной, а будет равно одному из двух значений: Х или х + 1, где
2х <
лт < 2Х+1
Например, если число ищется в диапазоне от 1 до 7, то его можно угадать за 2 или 3 вопроса, поскольку 22 2 3 .
Число из диапазона от 1 до 200 можно угадать за 7 или 8 
вопросов,
поскольку
Проверьте эти утверждения экспериментально!
Половинным делением можно искать, например, нужную страницу в толстой книге: открыть книгу посередине, понять, в какой из половин находится искомая страница. Затем открыть середину этой половины и т. д.
Набор данных может быть упорядочен не только по числовому ключу. Другой вариант упорядочения — по алфавиту.
МетоД половинного Деления является универсальным методом поиска для любых упорядоченных наборов Данных.
Блочный поиск
Снова вспомним пример с записной книжкой. Пусть в вашей записной книжке имеется алфавитный инДекс в виде вырезанной «лесенки» или в виде букв вверху страниц. Несколько страниц, помеченных одной буквой, назовем блоком. Имеется блок «А», блок «Б» и т. д. до блока «Я».
Алфавитный индекс это часть ключа поиска (например, первая буква).
|
Алгоритмы обработки информации |
|
|
1) с помощью алфавитного индекса выбирается блок с нужной буквой;
2) внутри блока поиск производится путем последовательного перебора.
Большинство книг в начале или в конце текста содержат оглавления: список названий разделов с указанием страниц, с которых они начинаются. Разделы это те же блоки. Поиск нужной информации в книге начинается с просмотра оглавления, с дальнейшим переходом к нужному разделу, который затем просматривается последовательно. Очевидно, это тот же блочнопоследовательный метод поиска.
Списки с указанием на блоки данных называются списками указателей.
Разбиение данных на блоки может быть многоуровневым. В толстых словарях блок на букву «А» разбивается, например, на блоки по второй букве: блок от «АБ» до «АЖ», следующий блок — от «АЗ» до «АН» и т. д. Слова внутри блока упорядочены по всем другим буквам. Такой порядок называется лексикоВ поисковом множестве с многоуровневой блочной структурой происходит поиск методом спуска: сначала отыскивается нужный блок первого уровня, затем второго и т. д. Внутри блока последнего уровня может происходить либо последовательный поиск (если данных в нем относительно немного), либо оптимизированный поиск типа половинного деления. Поиску методом спуска часто помогают многоуровневые списки указателей.
Поиск в иерархической структуре данных
|
|
Теоретические основы информатики |
 |
Рис. 1-29. Дерево каталогов
На местоположение файла в иерархической структуре указывает путь к файлу. Операционная система поможет найти нужный вам файл по команде «Поиск». Результат поиска представляется в виде пути к файлу, от корневого каталога последовательно по уровням дерева до каталога (папки), непосредственно содержащего ваш файл. Например, при поиске файла с именем Ке.ехе будет выдан следующий ответ:
Здесь указан полный путь к файлу на логическом диске Е: от корневого каталога до самого файла. Имея такую подсказку, вы легко отыщете нужный файл на диске методом спуска по Дереву каталогов. Каталог иерархической структуры файловой системы компьютера является многоуровневым списком указателей.
|
|
163 |
 |
|
|
Поиск данных |
||
|
|
Атриб ы поиска |
||
|
Набо Данных |
КЛЮч поиска |
Критерий поиска |
|
|
Вся совокупность данных, среди которых осуществляется поиск |
Поле записи, по значению которого происходит поиск |
Условие, которому должно удовлетворять значение ключа поиска в искомой записи |
|
|
|
Организация набора данных |
||
|
Неструктурированный набор |
Структура данных |
||
|
|
Линейная упорядоченность по ключу |
Блочная одноуровневая структура |
Блочная многоуровневая (иерархическая) структура |
|
|
Алгоритмы поиска |
||
|
Случайный перебор. Последовательный перебор |
Поиск половин- ным делением |
Блочно-последовательный поиск. Использование индексов и списков указателей |
Поиск методом спуска по дереву. Использование многоуровневых индексов и списков указателей |
Вопросы и задания
1. Что относится к атрибутам поиска?
2. Приведите примеры неорганизованных и структурированных наборов данных, помимо тех, что даны в тексте параграфа.
З. В журнале успеваемости учащихся со сведениями о годовых оценках требуется осуществить поиск всех отличников по информатике. Что в этой ситуации является набором данных, что ключом поиска, что — критерием поиска?
4. Попробуите внести изменение в блок-схему на рис. 1.27 так, чтобы алгоритм учитывал возможность выбора нескольких элементов набора данных, удовлетворяющих одному и тому же значению критерия поиска. Например, решите задачу поиска из предыдущего задания.
5. На старых школьных компьютерах («Корвет», «Электроника-УКНЦ» и др.) файловая система была организована так. На компьютере могло быть два дисковода: А: и В:. Имена всех файлов в каталоге одного диска составляли линейную последовательность. Полное имя файла выглядело, например, так: A:file1 .dat или B:file2.txt. К какому типу структур относится организация файлов на этих компьютерах?
6. Что такое список указателей? Посмотрите свои учебники по разным предметам. Определите, какие списки указателей там использованы: простые или многоуровневые.
7. Если у вас есть многотомная энциклопедия, посмотрите, как структурирована в ней информация. Что здесь является блоком первого уровня?
8. Можно ли каталог библиотеки назвать списком указателей? Почему? Если да, то какой он: простой или многоуровневый?
1 .7.6. Программирование поиска
|
|
Теоретические основы информатики |
|
164 |
 |
количество очков в турнирной таблице;
название вещества 
удельный вес; название товара цена товара
и т. д. Во всех этих примерах характеристики объектов являются числами, а имена
— текстами (словами).
Конечно, так бывает не всегда, кроме того, характеристик может быть несколько. Например: название вещества удельный вес теплоемкость удельное сопротивление, Здесь три характеристики. Имя также может быть составным. Например: фамилия, имя, отчество учителя. В последующих примерах мы ограничимся простейшим вариантом: имя символьная последовательность (слово), характеристика — число.
В качестве примера рассмотрим таблицу футбольного чемпионата премьер-лиги России за 2008 год. На рисунке 1.30 в столбце А находятся названия команд, в столбце В — набранные ими очки. Данные отсортированы по убыванию количества очков, поскольку именно в таком виде обычно представляются результаты чемпионата. Победители находятся в начале такой таблицы, а аутсайдеры — в конце.
Такую информацию удобно занести в электронную таблицу. В результате информация становится обозримой. Кроме того, таблицу можно сортировать в любом порядке по любому полю («Команды» или «Очки»), анализируя таким образом результаты чемпионата. В электронных таблицах также реализованы методы фильтрации, позволяющие выбирать из нее нужные подмножества данных. Все эти сортировки и фильтрации осуществляются
|
|
|
в |
|
|
Команды |
Очки |
|
1 |
Рубин |
60 |
|
2 |
ЦСКА |
56 |
|
3 |
Динамо |
|
|
4 |
Амкар |
51 |
|
5 |
Зенит |
48 |
|
6 |
Крылья Советов |
48 |
|
7 |
Локомотив |
47 |
|
8 |
Спартак-Москва |
|
|
9 |
Москва |
38 |
|
10 |
Терек |
35 |
|
11 |
Сатурн |
33 |
|
12 |
Спартак-Нальчик |
32 |
|
13 |
Томь |
29 |
|
14 |
Химки |
27 |
|
15 |
Шинник |
22 |
|
16 |
Луч-Энергия |
21 |
Рис. 1-30. Таблица чемпионата
программным путем по определенным алгоритмам, которые «не видны» пользователю. Пользователь видит лишь результат их выполнения.
Рассмотрим реализацию на языке программирования алгоритмов поиска, описанных в параграфе 1.7.5.
|
Алгоритмы обработки информации |
|
 |
Задача, Определить, какое количество очков набрала команда с данным названием (например, Амкар).
В языках программирования хранение таблиц организуется в
массивах. Если это линейная таблица, как в нашем примере, то такой массив
является оДномерным. Элементы массива имеют одинаковый тип данных. Элементы
массива Р имеют целый числовой тип (integer или byte). Элементы массива Теат 
символьные
строки (string). Одна величина типа string может представлять собой цепочку
символов компьютерного символьного алфавита длиной до 255.
Реализуем на Паскале два варианта алгоритма поиска: алгоритм последовательного поиска и алгоритм бинарного поиска (поиска половинным делением).
Программирование последовательного поиска
Ключом поиска является название команды. Пусть название искомой команды заносится в строковую переменную Х. Тогда критерием поиска будет совпадение значения переменной Х с одним из элементов массива Теат. Если номер этого элемента равен i, то искомое количество очков будет извлечено из i-I'0 элемента массива Р.
Поскольку исходные данные не отсортированы по значениям ключевого поля Теат, для поиска пригоден только алгоритм последовательного перебора. В следующей программе такой алгоритм реализован на Паскале. Program Premier 1iga; const б; Число команд}
|
|
Теоретические основы информатики |
 |
Теат: array[1. .N] of string[20] ; {
Таблица команд 
Х: strinq[20] ; Искомая команда } i: integer; F1ag: boolean; begin
Write1n
( Введите: команда — ОЧКИ! ) ; for i:=1 to do { Цикл ввода исходных
данных} begin
Write (1, Команда: Read (Team[i] ) ;
Write( Очки: ' ) ; Read1n (Р [1] ) end;
Write ( ' Введите название команды: ) ;
Readln (Х) ; {Ввод названия искомой команды)
F1ag: =false; 1 О 
whi1e( (i<N) апа пое F1ag) do {
Цикл поиска 
begin
(Если
команда найдена в таблице } if (Х=Теат ) then F1ag:= true end ; if (F1ag) then
Write1n (Х, имеет ' , Р Д] , очков ) e1se Write1n (Х, нет в таблице 
епа
.
Переменные Теат и Р описаны как одномерные массивы, состоящие из лт элементов. Элементы массива Р — целые величины типа byte. Тип элементов массива Теат — string [20). Это значит, каждое значение может быть строкой, содержащей не более 20 символов. Для названий футбольных команд этого достаточно.
В этой программе переменная i играет роль счетчика просматриваемых команд в таблице Теат. Логической переменной Flag в начале присваивается значение false. Когда же название искомой команды совпадет с названием i-ii команды в таблице Теат, переменная Flag примет значение true. После этого условие выполнения цикла whi1e ( (i<N) апа пое F1ag) станет ложным и цикл завершит свою работу.
Затем по значению переменной Flag определяется, наидена ли в таблице искомая команда. Если Flag = true, то в i-M элементе массива Теат обнаружена команда с названием Х. Следовательно, P[i] содержит набранные ею баллы. В противном случае выводится сообщение о том, что такой команды нет в таблице. Рассмотрим примеры вариантов тестов.
Терт 1.
Введите : команда очки
1 Команда : Рубин
|
Алгоритмы обработки информации |
|
 |
16 Команда : Луч—Энергия
Очки : 21
|
Введите название |
команды: |
Амкар |
|
Амкар имеет 51 тест 2. |
очков |
|
|
Введите название |
команды : |
Вымпел |
|
Вымпел нет в таблице |
||
Программирование бинарного поиска
Теперь представим себе, что исходные данные
отсортированы в алфавитном порядке названий команд, как это показано на рис.
1.31. В предыдущем параграфе говорилось о том, что в случае упорядоченных
значений ключевого поля для поиска можно использовать рациональный алгоритм
половинного деления 
бинарный поиск.
|
|
|
в |
|
|
Команды |
Очки |
|
1 |
Амкар |
51 |
|
2 |
Динамо |
54 |
|
З |
Зенит |
48 |
|
4 |
Крылья Советов |
48 |
|
5 |
Локомотив |
47 |
|
6 |
Луч-Энергия |
21 |
|
7 |
Москва |
38 |
|
8 |
Рубин |
60 |
|
9 |
Сатурн |
33 |
|
10 |
Спартак-Москва |
|
|
11 |
Спартак-Нальчик |
32 |
|
12 |
Терек |
35 |
|
13 |
Томь |
29 |
|
14 |
Химки |
27 |
|
15 |
ЦСКА |
56 |
|
16 |
Шинник |
22 |
Рис. 1.31. Таблица чемпионата
Алгоритм бинарного поиска запрограммирован в следующей программе на Паскале. Program Premier 1iga 2;
Const М=1, N=16;
Var Р: array [М. .N] 0f byte;
Теат: array [М. .N] of string [20] ;
Х: string[20] ;
|
|
Теоретические основы информатики |
 |
Write1n
( Введите: команда — очки!) ; for 
begin
Write
(1, Команда: Read 
) ;
Write( ' Очки: Readln (Р Д] ) end;
Write ( ' Введите название команды: ) ; Read1n (Х) ;
L:=M; R:=N; {L — левая граница интервала; R — правая граница}
{ Цикл повторяется, пока границы не совпадут}
while ( (R—L) do beg in
(R+L) div 2 ; [Нахождение номера средней
точки}
Перемещение
одной из границ} if (Х<=Теат [К] ) then R :=k e1se 
end; if 
then
Write1n (Х, имеет! , P(R] , очков ' ) else Write1n (Х, нет в таблице ' ) end.
|
Алгоритмы обработки информации |
|
 |
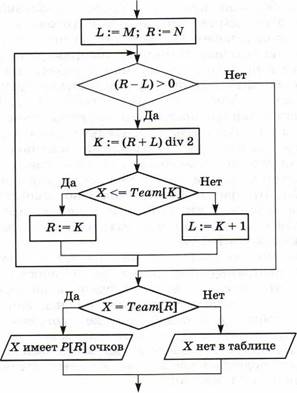
рис. 1.32. Блок-схема бинарного поиска
Идея алгоритма заключается в следующем. Интервалом поиска назовем диапазон номеров элементов массива Теат, в котором происходит поиск. Левая граница интервала в начале поиска равна М, правая граница — N. Значение левой границы заносится в переменную L, значение правой границы — в переменную R
При каждом повторении цикла границы будут приближаться друг к другу, уменьшая интервал в два раза. Цикл закончится, когда границы совпадут, т. е. L станет равным R. Если после этого значение Теат[Щ совпадет со значением Х — названием искомой команды, то команда найдена и в переменной P[R] находится искомое число очков. Если Теат[Щ не совпадет с Х, то это значит, что в таблице нет такой команды.
В условном операторе if использовано отношение сравнения строковых величин: Х<=Теат[К]. Символьные строки можно сравнивать на равенство/неравенство, а также на больше/меньше. Сравнение строк происходит посимвольно слева направо. Большей считается та строка, в которой первый несовпадающий символ имеет больший номер в таблице символьной кодировки.
|
|
Теоретические основы информатики |
 |
У этой программы есть «подводный камень». Возможность использования русских слов зависит от того, какая кодовая страница используется данной системой программирования (см. параграф 1.4.2)). Программа будет правильно работать, если кодовая страница содержит кириллицу и в ней выдержан принцип последовательного кодирования алфавита. Такое правило, например, выполняется в СР-1251.
Программу можно протестировать на тех же данных, что и предыдущую программу последовательного поиска. Отличие состоит в том, что вводить таблицы нужно в последовательности отсортированных по алфавиту названий команд, как на рис. 1.31.
Для того чтобы при каждом запуске программы не вводить вручную таблицы, их следует один раз записать в текстовый файл и ввод данных производить из этого файла. О работе с файлами будет подробно рассказано в главе, посвященной программированию (в 11 классе).
Система основных понятий
|
Программирование поиска данных |
|
|
Организация данных |
Сортируемые данные заносятся в массивы |
|
Программа последовательного поиска |
Имеет циклическую структуру. Для фиксации найденного значения используется логическая переменная Flag, Если значение наидено, Flag принимает значение true |
|
Программа бинарного поиска |
Интервал поиска —
диапазон номеров элементов просматриваемого массива. 1., — нижняя граница, R
— верхняя граница. Программа имеет циклическую структуру. На каждом шаге
цикла интервал сокращается в 2 раза, значения Т., = R, искомый элемент найден |
Вопросы и задания
1. Что такое одномерный массив? Как идентифицируются элементы одномерного массива?
2. Какие значения может принимать величина строкового типа?
|
Алгоритмы обработки информации |
 |
4. 
Какое значение примет логическое
выражение (i<N) and пое F1ag, если i = 5, = 16, Flag = false?
5. Какие значения примут переменные R и в программе Premier 1 iga 2 после выполнения операторов:
К:= (R+L) div 2; if 
[К] ) then R : =k else 
если первоначальные значения были: R
= 16, 1., = 8 и условие 
[К] оказалось: а) истинным, б) ложным?
Практикум. Раздел 5 «Программирование»
1 .7.7. Алгоритмы сортировки данных
Сортировкой называют упорядочение данных по некоторому признаку. Сортировку часто приходится выполнять в компьютерных базах данных, информационно-справочных системах. От эффективности алгоритмов сортировки, прежде всего, от скорости их выполнения во многом зависит эффективность работы всей программы.
Различают алгоритмы внутренней сортировки сортировки во внутренней памяти компьютера и внешней сортировки — сортировки информации в файлах. Здесь мы будем говорить только о внутренней сортировке.
Как правило, сортируемые данные располагаются в массивах. Это могут быть массивы как с числовой, так и с символьной информацией. В качестве примера будем рассматривать те же данные, что в предыдущем параграфе: таблицу футбольного чемпионата.
В таблице на рис. 1.30 данные отсортированы в порядке убывания набранных очков. В таком случае поле «Очки» являлось ключом сортировки. А поряДок сортировки произведен по убыванин) значения ключа. В таблице на рис. 1.31 ключом сортировки является название команды, порядок сортировки — по возрастаник», т. е. в алфавитном порядке.
Рассмотрим два алгоритма сортировки: сортировку методом выбора максимального элемента и сортировку методом пузырька.
Сортировка выбором максимального элемента
Исходными данными задачи является таблица на рис. 1.31. Ее нужно отсортировать в порядке убывания значений набранных очков, т. е. превратить в таблицу на рис. 1.30.
|
|
Теоретические основы информатики |
 |
Идея алгоритма заключается в следующем. В массиве Р ищется номер первого по порядку элемента с максимальным значением. После этого производится перестановка значений элемента с этим номером и элемента Р[1]. Одновременно переставляются значения элементов с такими же номерами в массиве Теат. Значения первых элементов массивов оказались на своих местах. Затем ищется номер первого максимального элемента в массиве Р, начиная с Р[2]. Производится перестановка значения этого элемента с значением элемента Р[2]. Значение второго элемента на своем месте. Затем ищется максимальный элемент, начиная с Р[З]. И так далее. Процесс закончится, когда упорядочатся значения последней пары элементов: P[N— 1] и P[N].
Вот программа на Паскале, реализующая
данный метод сортировки. Proqram Sort 1;
Const N=16;
Var Р: array[1. .N] 0f byte;
Теат: array[1. .N) of string [20) ;
Х, i, К, ј : byte; begin
for i:=1 €0 do
begin
Write (1, Команда : ' ) ; Read1n 
) ;
Write Очки: ; Read1n
(Р [1] ) end; for 
N-1 do { Внешний цикл сортировки} begin
К: {Номер первого анализируемого элемента массива) forЕо do внутренний цикл сортировки} if (Р [ј ] >Р (К] ) then К:=ј; (Конец внутреннего цикла}
Теат[К] :=str end; {
Конец внешнего цикла)
[Вывод результата: отсортированных
массивов 
Write1n ( Результат: ' ) ; for to N do
|
Алгоритмы обработки информации |
|
 |
end.
В алгоритме сортировки имеются два вложенных цикла. Внешний цикл по параметру i повторяет свое выполнение N—1 раз. В результате каждого выполнения на места i-x элементов в массивах Р и Теат попадают нужные значения. Во внутреннем цикле в переменной отбирается номер первого из максимальных значений среди элементов массива Р, от (i + 1)-го до ЛТ-го. В конце программы выводятся на экран отсортированные по очкам таблицы Теат и Р, как это представлено на рис. 1.30.
Сортировка методом пузырька
Идею сортировки методом пузырька проиллюстрируем на наглядном примере. Дан неупорядоченный массив чисел Р из четырех элементов. Нужно отсортировать его значения по убыванию. Процесс сортировки методом пузырька показан в табл. 1.20. Таблица 1.20
Сортировка методом пузырька
|
|
|
|
|
|
|
|
|
|
Исходные данные |
1 |
з |
2 |
4 |
|||
|
1-й проход |
1-й шаг |
з |
1 |
2 |
4 |
||
|
2-й шаг |
з |
2 |
1 |
4 |
|||
|
3-й шаг |
з |
2 |
4 |
1 |
|||
|
2-й проход |
4-й шаг |
з |
2 |
4 |
1 |
||
|
5-й шаг |
з |
4 |
2 |
1 |
|||
|
3-й ход |
6-й шаг |
4 |
з |
2 |
1 |
||
На первом шаге сравниваются между собой значения 1-го и 2-го элементов и упорядочиваются по убыванию: если Р[1]<Р[2], то переставляются, иначе остаются на месте. На втором шаге упорядочиваются значения элементов Р[2] и Р[З]. На третьем шаге — Р[З] и Р[4]. В результате минимальное значение попадает на свое место — в элемент Р[4]. Шаги с 1-го по 3-й назовем первым проходом массива.
На четвертом и пятом шагах повторяются такие же парные сортировки, после чего устанавливается значение элемента Р[З]. Это второй проход массива.
На последнем, шестом шаге упорядочивается пара значений Р[1] и Р[2]. Это последний, третий проход массива. В результате весь массив оказывается отсортированным по убыванию значений.
Если размер массива равен N, то число сортирующих проходов равно N— 1. Причем количество шагов каждого следующего прохода на единицу меньше предыдущего.
Для сортировки по возрастанию следует перемещать вправо большее значение в каждой сравниваемой паре.
|
|
Теоретические основы информатики |
|
лируются для соответствующих элементов массива Теат.
в Ниже приведена программа на Паскале, реализующая метод пузырька.
Program Sort 2;
Const N=16;
Var Р: array[1. .N] of byte;
Теат: array[1. .N) of string[20] ; str: string[20) ;
Х, 1, ј : byte; begin 
Write1n ( ' Введите : команда —
очки ; (Ввод исходных данных for i:=1 Ео N do begin 
Write (i, ' Команда: Read1n (ТеатД] ) ;
Write( Очки: Read1n (Р Д] ) end; for i:=1 €0 N—1 do — номер сортирующего прохода } begin for ј Ео N—i do {Ј — номер шага сортировки)
Теат[ј+1] :=str end end;
{ Вывод результатов: отсортированных массивов) for €0 N do
Write1n а: З, Теат [1] , 
end.
|
Алгоритмы обработки информации |
|
 |
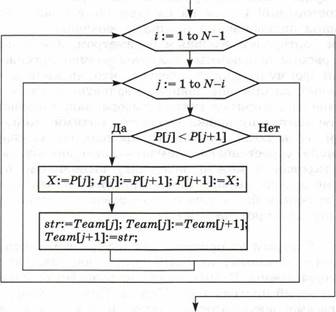
Рис. 1 .ЗЗ. Сортировка методом пузырька
В блок-схемах вытянутым шестиугольником обозначается заголовок цикла с параметром, который программируется в Паскале оператором for.
Структура алгоритма: два вложенных цикла с вложенным неполным ветвлением. Длина внутреннего цикла сокращается на единицу с увеличением значения i — параметра внешнего цикла.
Сравнение алгоритмов сортировки
Временная сложность циклических алгоритмов определяется количеством повторений выполнения циклов. В обоих рассмотренных алгоритмах имеются по два вложенных цикла. Внешний цикл по параметру i повторяется лт — 1 раз, внутренний цикл для каждого значения параметра повторяется лг — i раз. Следовательно, полное число повторений циклов равно: S = (N — 1) + + (N — 2) + (N — 3) + + 2 + 1 раз. Это сумма арифметической прогрессии. Используя известную формулу, получим:
N(N-1)
2 2 2
Например, для лт = 16 по данной формуле получим S = 120.
Надо сказать, что это довольно большое значение. Подсчитайте, каким будет число повторений циклов при лт = 100. Получится 4950 повторений! И еще на каждом шаге цикла выполняется шесть команд присваивания и одна — сравнения.
В задаче сортировки основным параметром, влияющим на длительность работы программы, является размер массива — N. Из полученной формулы для S следует, что временная сложность рассмотренных алгоритмов зависит квадратично от N.
|
|
Теоретические основы информатики |
 |
Наиболее быстрым алгоритмом для внутренней сортировки данных является алгоритм, который так и называется: алгоритм быстрой сортировки. В 1960 году его разработал известный английский ученый-программист Чарльз Энтони Хоар. Здесь мы не будем рассматривать этот алгоритм. К нему мы вернемся в 11 классе. Скажем только, что его временная сложность пропорциональна величине N•lnN. Чем больше N, тем больше значение такой функции отличается от N2 . Например:
лт = 10, № = 100, N•lnN = 23,03;
= 100, № = 10 000, N•lnN = 460,52.
Следовательно, чем больше размер массива, тем выгоднее становится применение алгоритма быстрой сортировки по сравнению с алгоритмами выбора максимального элемента и метода пузырька.
Система осНоВНЫХ понятий
|
Алгоритмы сортировки |
|
|
Сортировка — упорядочение данных по некоторому признаку |
|
|
Параметры сортировки |
|
|
Ключ сортировки: поле данных, по значению которого производится сортировка |
ПоряДок сортировки: по возрастанию значений ключа, по убыванию значений ключа |
|
Методы сортировки |
|
|
Выбор максимального элемента |
Метод пузырька |
|
Два вложенных цикла. На каждом шаге внешнего цикла находится первый максимальный элемент неупорядоченной части массива и ставится на свое место в отсортированном массиве |
лт — размер массива. Два вложенных цикла. Внешний цикл организует лт — 1 проход по неотсортированной части массива. На каждом шаге внутреннего цикла упорядочиваются соседние пары элементов |
|
Оба метода имеют временную сложность -- N2 |
|
|
Метод быстрой сортировки Хоара имеет временную сложность N•lnN |
|
|
Алгоритмы обработки информации |
|
|
|
177 |
Вопросы и задания
1. Что такое сортировка, ключ сортировки, порядок сортировки?
2.
Как определяется 
сложность циклических алгоритмов? От
какого параметра она зависит в первую очередь?
Практикум. Раздел 5
«Программирование»
ЭОР к главе 1 на сайте ФЦИОР (http://fcior.edu.ru)
1.1.
Что изучает «Информатика»
Информация,
информационные процессы в обществе, природе и технике
Виды и свойства
информации
1.2.
Единицы измерения
информации
1.3.
Принцип
дискретного (цифрового) представления информации, системы счисления, алгоритмы
Понятие о
системах счисления
Представление
числовой информации с помощью систем счисления. Алфавит, базис, основание.
Свернутая и развернутая форма представления чисел
Арифметические
операции в позиционных системах счисления 
Связь между двоичной, восьмеричной и
шестнадцатеричной системами счисления
Достоинства и
недостатки двоичной системы счисления при использовании ее в компьютере
1.4.
Представление
текста в различных кодировках
Растровая и
векторная графика
Аппаратное и
программное обеспечение для представления изображения
Аппаратное и
программное обеспечение для представления звука
1.5.
Информация и
информационные процессы
Классификация
информационных процессов
1.6.
Высказывание.
Простые и сложные высказывания. Основные логические операции 
Теория мноэкеств
Логические законы
и правила преобразования логических выражений 
Построение отрицания к простым
высказываниям, записанным на русском языке 
Построение отрицания к сложным
высказываниям, записанным на русском языке
|
|
Теоретические основы информатики |
Решение
логических задач
1.7.
Алгоритмы
сортировки
Алгоритмы поиска
178
От авторов
Глава 1 . Теоретические основы информатики .
1.1. Информатика и информация .
7
1.2. Измерение информации
12
1.2.1. Алфавитный подход к измерению
информации
12
 |
16
1.2.3. Вероятность и информация
.
24
1.3. Системы счисления .
зо
1.3.1. Основные понятия систем счисления .
.
зо
1.3.2. Перевод десятичных чисел в
другие системы счисления
36
1.3.3. Автоматизация перевода чисел из
системы в систему . . .. 39 
Смешанные системы счисления
43
1.3.5. Арифметика в позиционных
системах счисления . .
. 47
1.4. Кодирование.
52
1.4.1. Информация и сигналы
. 52
1.4.2. Кодирование текстовой информации. .
. . . . .
56
1.4.3. Кодирование изображения 63
1.4.4. Кодирование звука68
1.4.5.
Сжатие двоичного кода....... . 74
1.5. Информационные процессы.
81
1.5.1. Хранение информации .
81
1.5.2. Передача информации
86
1.5.3. Коррекция ошибок при передаче
данных
91
1.5.4. Обработка информации .
97
1.6. Логические основы обработки информации 104
1.6.1. Логика и логические операции
1.6.2. Логические формулы и функции
1.6.3. Логические формулы и
логические схемы .
1.6.4. Методы решения логических задач
1.6.5. Логические функции на области
числовых значений . 
.
129
|
|
Оглавление |
 |
Алгоритмы
обработки информации.
135
1.7.1. Определение, свойства и описание алгоритма. . . 135
1.7.2. Алгоритмическая машина Тьюринга .
141
1.7.3. Алгоритмическая машина Поста
146
1.7.4. Этапы алгоритмического решения задачи 
,
150
1.7.5. Алгоритмы поиска данных
156
1.7.6. Программирование поиска
164
1.7.7. Алгоритмы сортировки данных. . . . . .
. .
171
[1] ) перевести данные числа в двоичную систему счисления, используя таблицу двоично-р-ичной смешанной системы;
[2] о 1 2 о 1
|
Вычисления в системах счисления с основанием р |
2 П мож- |
но производить по такой же схеме, как это делалось выше: построить таблицы сложения и умножения и, заглядывая в эти таблицы, выполнять многозначные вычисления. Но можно пойти другим путем, используя связь таких систем с двоичной системой счисления. Алгоритм вычисления будет следующим:
[3] ) выполнить вычисления с двоичными числами;
З) перевести полученное двоичное число в р-ичную систему через ту же таблицу.
[4] ) Подробнее о проблеме алгоритмической неразрешимости см.:
Андреева Е. В., Босова Л. Л., Фалина И. Н. Математические основы информатики. Элективный курс. — М.: БИНОМ. Лаборатория знаний, 2007; Энциклопедия школьной информатики/Под ред. И. Г. Семакина. — М.: БИНОМ. Лаборатория знаний, 2011.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
F1
= 1, Ъ = 2, F3=F2 +F1, 
Fi = Fi_1 + 1, 2, з, 5, 8, 13, 21, 34,
... числа Фибоначчи
шаг 1
