Сфираль и квантовые вычисления: формальная модель

О.С. Басаргин, 6 марта 2025 

Введение 

Современные квантовые вычисления стремятся к созданию устойчивых архитектур кубитов, способных эффективно обрабатывать и защищать информацию. В данной работе представляется формальная модель Сфирали как нового метода организации квантовых состояний, основанного на зеркальной антисимметрии, S-образных переходах и фрактальной структуре.

1.   Математическая основа Сфирали

1.1.   S-образные переходы и операторы квантовой эволюции

S-образные переходы можно рассматривать как обобщение традиционных квантовых гейтов, таких как Hadamard и Pauli-X, в многомерном пространстве состояний. В отличие от дискретных операций, применяемых в стандартных квантовых схемах, S-образные переходы представляют собой непрерывные трансформации, которые могут быть использованы для плавного переноса информации между квантовыми состояниями, обеспечивая дополнительную топологическую защиту и устойчивость к внешним возмущениям. Пусть ∣ψ⟩ – состояние кубита, тогда S-образный переход можно выразить через оператор S, связанный с изменением фазовой структуры:

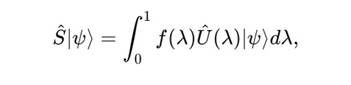
где λ – параметр эволюции, U (λ) – унитарное преобразование, а f (λ) – весовая функция, определяющая плавность перехода.

1.2.   Фрактальная структура кубитов

Фрактальная природа Сфирали учитывается через вложенные состояния ∣ψ_n):

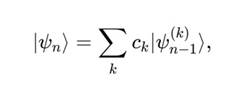
где каждый уровень n зависит от предыдущего через коэффициенты c_k, отражающие корреляции в многомерном пространстве.

2.   Запутанность и топологическая защита

Связь предложенного подхода с топологическими квантовыми вычислениями, в частности с моделью Майораны, заключается в использовании топологической устойчивости состояний. В модели Майораны информация хранится в фермионном паритете двух пространственно разделённых нулевых мод, что обеспечивает защиту от локальных помех. В Сфирали аналогичная защита достигается за счёт зеркальной антисимметрии и фрактальной структуры кубитов, что позволяет распределять информацию по многомерному пространству состояний и снижает вероятность декогеренции.

2.1.          Связь между сфиральными координатами и квантовой запутанностью

Координаты (r,θ,ϕ,ψ,n) описывают состояния кубитов, где ψ – параметр витка, а n – уровень фрактальности. Запутанность можно выразить как топологический инвариант:

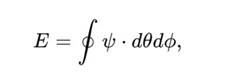
где E остаётся неизменным при локальных деформациях параметрического пространства.

2.2.   Топологическая устойчивость сфиральных кубитов

Кубиты в модели Сфирали описываются как узлы в многомерном пространстве. Их устойчивость обеспечивается зеркальной антисимметрией:

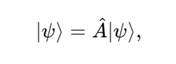
где оператор A соответствует отражению в пространстве Сфирали, создавая стабильные корреляции между состояниями.

3.   Применение в квантовых алгоритмах

3.1.   Операции квантовой логики

S-образные переходы можно использовать для реализации универсальных квантовых гейтов:

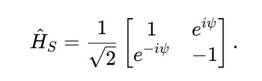
Это позволяет реализовать аналоги гейтов Адамара и CNOT, но с дополнительной топологической защитой.

Данный подход также может быть использован в практических квантовых алгоритмах, таких как факторизация (алгоритм Шора) и квантовый поиск (алгоритм Гровера). Например, в алгоритме Шора Сфиральные переходы могут оптимизировать представление чисел в фрактальном пространстве состояний, снижая сложность вычислений. В алгоритме Гровера зеркальная антисимметрия и многомерная запутанность позволяют более эффективно проводить амплитудное усиление, повышая вероятность нахождения решения.

3.2.   Оптимизация квантовых вычислений

Использование фрактальной структуры снижает энергетические затраты на коррекцию ошибок, а зеркальная антисимметрия повышает точность вычислений, что делает Сфираль перспективной основой для масштабируемых квантовых систем.

Заключение 

Представленная модель демонстрирует потенциал Сфирали в квантовых вычислениях, объединяя топологическую защиту, фрактальную структуру и S-образные переходы. Дальнейшие исследования сфокусируются на физической реализации этих идей и проверке их экспериментальными методами.