Симметрия

СИММЕТРИЯ Автор: Лякина Соня 6 «А» класс. «… быть прекрасным значит быть симметричным и соразмерным» (Платон )

Симметрия «Симметрия» - соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости.

История термина «симметрия». Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик В. И. Вернадский (1863—1945), «слагалось в течение десятков, сотен, тысяч поколений". «Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта. У древних народов Атлантиды, как стало известно учёным по найденным рукописям термин «симметрия» означал совершенство, а по найденным фигуркам, статуэткам и другим вещам, стало ясно, что в древней Атлантиде было всё строго симметрично. Кристаллы наделены наибольшей величиной симметрии из всех реальных объектов. Почти все кристаллы, встречающиеся в природе имеют центр, ось и плоскость симметрии. Поражающие правильные очертания кристаллов вызывали в древности суеверные представления. Такое могли сотворить только ангелы или подземные духи - утверждали наши предки, Красота и гармония природной симметрии наталкивала даже испытанных мудрецов на  самые  фантастические мысли. Законы природы являются симметричными, но при ближайшем их рассмотрении, в каждом из них можно найти хоть небольшой изъян. Оказывается, что природа не терпит точной симметрии. Природа почти, но не абсолютно симметрична. Примером этому являются догадки Пифагора, который считал, что орбиты, по которым движутся планеты, являются совершенными окружностями, на самом же деле это не так. Или если мы посмотрим на человека – внешне он симметричен, но строение органов и их расположение абсолютно ассиметрично.

К простейшим типам пространственной симметрии относятся: зеркальная (порожденная отражениями) осевая; центральная;

Зеркальная симметрия Зеркальная симметрия в геометрии часто ассоциируется у нас с правильными многоугольниками, но если присмотреться, эти фигуры довольно часто встречаются в природе. Одни из них можно увидеть в виде кристаллов, другие – в виде простейших микроорганизмов или вирусов. Зеркальная симметрия очень часто встречается в архитектуре. Зеркальная симметрия в геометрии часто ассоциируется у нас с правильными многоугольниками, но если присмотреться, эти фигуры довольно часто встречаются в природе. Одни из них можно увидеть в виде кристаллов, другие – в виде простейших микроорганизмов или вирусов. Зеркальная симметрия очень часто встречается в архитектуре.

Осевая симметрия Симметрия относительно оси или линии пересечения плоскостей называется осевой. Она предполагает, что если через каждую точку оси симметрии провести перпендикуляр, то на нем всегда можно найти 2 симметричные точки, расположенные на одинаковом расстоянии от оси. В правильных многоугольниках осями симметрии могут являться их диагонали или средние линии. В окружности оси симметрии - ее диагонали. Симметрия относительно оси или линии пересечения плоскостей называется осевой. Она предполагает, что если через каждую точку оси симметрии провести перпендикуляр, то на нем всегда можно найти 2 симметричные точки, расположенные на одинаковом расстоянии от оси. В правильных многоугольниках осями симметрии могут являться их диагонали или средние линии. В окружности оси симметрии - ее диагонали.

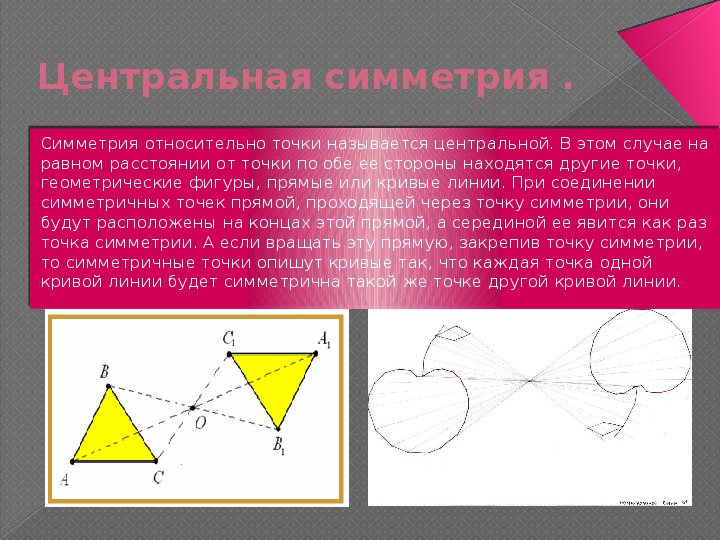
Центральная симметрия . Симметрия относительно точки называется центральной. В этом случае на равном расстоянии от точки по обе ее стороны находятся другие точки, геометрические фигуры, прямые или кривые линии. При соединении симметричных точек прямой, проходящей через точку симметрии, они будут расположены на концах этой прямой, а серединой ее явится как раз точка симметрии. А если вращать эту прямую, закрепив точку симметрии, то симметричные точки опишут кривые так, что каждая точка одной кривой линии будет симметрична такой же точке другой кривой линии. Симметрия относительно точки называется центральной. В этом случае на равном расстоянии от точки по обе ее стороны находятся другие точки, геометрические фигуры, прямые или кривые линии. При соединении симметричных точек прямой, проходящей через точку симметрии, они будут расположены на концах этой прямой, а серединой ее явится как раз точка симметрии. А если вращать эту прямую, закрепив точку симметрии, то симметричные точки опишут кривые так, что каждая точка одной кривой линии будет симметрична такой же точке другой кривой линии.

Движение плоскости - это отображение плоскости на себя, сохраняющее расстояния. Итак, осевая и центральная симметрия представляют собой отображение плоскости на себя, которое сохраняет расстояния между точками. В пространстве На плоскости На прямой Зеркальная Осевая Центральная Поворотная Центральная Центральная

Симметрия в алфавите. Одна из самых интересных для меня симметрий , является симметрия в алфавите.

СИ ММ ЕТ РИ Я БУ КВ Ы Буквы русского языка тоже можно рассмотреть с точки зрения симметрии. Вертикальная ось симметрии: А; Д; Л; М; П; Т; Ф; Ш. Горизонтальная ось симметрии: В; Е; З; К; С; Э; Ю. И вертикальные и горизонтальные оси симметрии: Ж; Н; О; Х. Ни вертикальные, ни горизонтальные оси: Б; Г; И; Й; Р; У; Ц; Ч; Щ; Я. В русском языке есть «симметричные» слова – палиндромы, которые можно читать одинаково в двух направлениях: шалаш, казак, радар, Алла, Анна, кок, поп. Могут быть палиндромическими и предложения. Написаны тысячи таких предложений. А роза упала на лапу Азора. Я иду с мечем судия. (Г. Р. Державин.) Буквы русского языка тоже можно рассмотреть с точки зрения симметрии. Вертикальная ось симметрии: А; Д; Л; М; П; Т; Ф; Ш. Горизонтальная ось симметрии: В; Е; З; К; С; Э; Ю. И вертикальные и горизонтальные оси симметрии: Ж; Н; О; Х. Ни вертикальные, ни горизонтальные оси: Б; Г; И; Й; Р; У; Ц; Ч; Щ; Я. В русском языке есть «симметричные» слова – палиндромы, которые можно читать одинаково в двух направлениях: шалаш, казак, радар, Алла, Анна, кок, поп. Могут быть палиндромическими и предложения. Написаны тысячи таких предложений. А роза упала на лапу Азора. Я иду с мечем судия. (Г. Р. Державин.)

СПАСИБО ЗА ВНИМАНИЕ !