Симплекс-метод

2. Компания производит два вида продукции, А и В. Объем продаж продукта А составляет не менее 80% от общего объема продаж продуктов А и В. Вместе с тем компания не может производить более 100 единиц продукта А в день. Для производства этих продуктов используется одно и то же сырье, поступление которого ограничено 240 тоннами в день. На изготовление единицы продукции А расходуется 2 тонны сырья, а единицы продукта В – 4 тонны. Цена одной единицы продуктов А и В составляет $20 и $50 соответственно.

а) Найдите оптимальную структуру производства этой компании.

b) Произвести анализ чувствительности изменения коэффициентов целевой функции.

с) Произвести анализ чувствительности запасов сырьевых ресурсов.

d) С помощью графического анализа чувственности определите, как изменится значение целевой функции при изменении максимального уровня производства продукта А на ±10 единиц.

Сделать выводы и записать рекомендации по производству и сбыту.

Решение:

а) Найдите оптимальную структуру производства этой компании.

Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.

Определим максимальное значение целевой функции F(X) = 20x₁+50x₂ при следующих условиях-ограничений.

2x₁+4x₂≤240

x₁≤100

20x1 >= 0.8(20x1+50x2) - ограничение про 80% объёма продаж товара A  ↔ -4x₁+40x₂≤0

2x₁+4x₂≤240

x₁≤100

-4x₁+40x₂≤0

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1-м неравенстве смысла (≤) вводим базисную переменную x₃. В 2-м неравенстве смысла (≤) вводим базисную переменную x₄. В 3-м неравенстве смысла (≤) вводим базисную переменную x₅.

2x₁+4x₂+x₃ = 240

x₁+x₄ = 100

-4x₁+40x₂+x₅ = 0

Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.

Решим систему уравнений относительно базисных переменных: x₃, x₄, x₅

Полагая, что свободные переменные равны 0, получим первый опорный план:
X₀ = (0,0,240,100,0)

Базисное решение называется допустимым, если оно неотрицательно.

Переходим к основному алгоритму симплекс-метода.
Итерация №0.

1.     Проверка критерия оптимальности.

2.     Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

2. Определение новой базисной переменной.

В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю.

3. Определение новой свободной переменной.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i2
и из них выберем наименьшее:
min (240 : 4 , - , 0 : 40 ) = 0

Следовательно, 3-ая строка является ведущей.

Разрешающий элемент равен (40) и находится на пересечении ведущего столбца и ведущей строки.

4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы. Вместо переменной x₅ в план 1 войдет переменная x₂.
Строка, соответствующая переменной x₂ в плане 1, получена в результате деления всех элементов строки x₅ плана 0 на разрешающий элемент РЭ=40. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₂ записываем нули.
Таким образом, в новом плане 1 заполнены строка x₂ и столбец x₂. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
СТЭ - элемент старого плана, РЭ - разрешающий элемент (40), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:

Получаем новую симплекс-таблицу:

Итерация №1.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения D_i по строкам как частное от деления: b_i / a_i1
и из них выберем наименьшее:
min (240 : 2²/₅ , 100 : 1 , - ) = 100
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (2²/₅) и находится на пересечении ведущего столбца и ведущей строки.

Поскольку в последнем столбце присутствует несколько минимальных элементов 100, то номер строки выбираем по правилу Креко.
Метод Креко заключается в следующем. Элементы строк, имеющие одинаковые наименьшие значения min=100, делятся на предполагаемые разрешающие элементы, а результаты заносятся в дополнительные строки. За ведущую строку выбирается та, в которой раньше встретится наименьшее частное при чтении таблицы слева направо по столбцам.
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы. Вместо переменной x₃ в план 2 войдет переменная x₁.
Строка, соответствующая переменной x₁ в плане 2, получена в результате деления всех элементов строки x₃ плана 1 на разрешающий элемент РЭ=2²/₅. На месте разрешающего элемента получаем 1. В остальных клетках столбца x₁ записываем нули.
Таким образом, в новом плане 2 заполнены строка x₁ и столбец x₁. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
Представим расчет каждого элемента в виде таблицы:

Получаем новую симплекс-таблицу:

1. Проверка критерия оптимальности.
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:

Оптимальный план можно записать так:

x₁ = 100, x₂ = 10

F(X) = 20*100 + 50*10 = 2500

Анализ оптимального плана.

Значение 0 в столбце x₁ означает, что использование x₁ - выгодно.

Значение 0 в столбце x₂ означает, что использование x₂ - выгодно.

Значение 10⁵/₁₂ в столбце x₃ означает, что теневая цена (двойственная оценка) равна y₁=10⁵/₁₂.

Значение 0 в столбце x₄ означает, что теневая цена (двойственная оценка) равна y₂=0.

Значение ⁵/₂₄ в столбце x₅ означает, что теневая цена (двойственная оценка) равна y₃=⁵/₂₄.

b) Произвести анализ чувствительности изменения коэффициентов целевой функции.

Изменение значений коэффициентов c₁ и c₂ приводит к изменению угла наклона прямой z. Существует интервалы изменения коэффициентов c₁ и c₂, когда текущее оптимальное решение сохраняется. Задача анализа чувствительности и состоит в получении такой информации. Необходимо определить интервал оптимальности для отношения c₁ / c₂ (или c₂ и c₁). Если значение отношения c₁ / c₂ не выходит за пределы этого интервала, то оптимальное решение в данной модели сохраняется неизменным.

Таким образом, в рамках анализа на чувствительность к изменениям коэффициентов целевой функции могут исследоваться вопросы:

1. Каков диапазон изменения того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения.

2. На сколько следует изменить тот или иной коэффициент целевой функции, чтобы изменить статус некоторого ресурса.

Функция достигает своего оптимума в точке, которая является пересечением прямых (2x₁+4x₂=240) и (x₁=100). При изменении коэффициентов целевой функции эта точка останется точкой оптимального решения до тех пор, пока угол наклона линии z будет лежать между углами наклона этих прямых. Алгебраически это можно записать следующим образом:

при условии c₁ ≠ 0

или

при условии c₂ ≠ 0

Таким образом, мы получили две системы неравенств, определяющих интервал оптимальности.

При c₂ = 50

или

0 ≤ c₁ ≤ 25

При c₁ = 20

или
0 ≤ c₂ ≤ 40

с) Произвести анализ чувствительности запасов сырьевых ресурсов.

На данном этапе важно проанализировать следующие аспекты:

1. На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции.

2. На сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции.

Оценка ресурса M1

Концевые точки отрезка определяют интервал осуществимости для ресурса M1.

Количество сырья, соответствующего точке (100,0), равно 2·100 + 4·0 = 200

Количество сырья, соответствующего точке (100,10), равно 2·100 + 4·10 = 240

Таким образом, интервал осуществимости для ресурса M1 составляет 200 ≤ M1 ≤ 240

Вычислим значение целевой функции в этих точках:

F(100,0) = 20·100 + 50·0 = 2000

F(100,10) = 20·100 + 50·10 = 2500

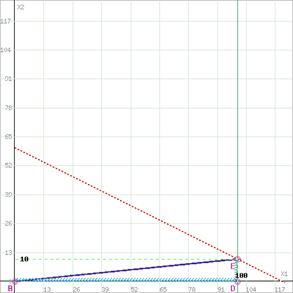
Изменение области решений при увеличении запасов ресурса M1

Оценка ресурса M2

Концевые точки отрезка определяют интервал осуществимости для ресурса M2.

Количество сырья, соответствующего точке (100,10), равно 1·100 + 0·10 = 100

Количество сырья, соответствующего точке (120,0), равно 1·120 + 0·0 = 120

Таким образом, интервал осуществимости для ресурса M2 составляет

100 ≤ M2 ≤ 120

Вычислим значение целевой функции в этих точках:

F(100,10) = 20·100 + 50·10 = 2500

F(120,0) = 20·120 + 50·0 = 2400

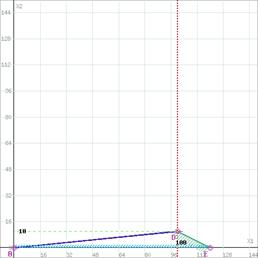
Изменение области решений при увеличении запасов ресурса M2

Рассмотрим теперь вопрос об уменьшении правой части неактивного ограничения (3). Не изменяя оптимального решения, прямую L3 можно опустить до пересечения с оптимальной точкой. При этом правая часть ограничения (3) станет равной -4x₁+40x₂=0, что позволит записать ограничение (1) в виде -4x₁+40x₂≤0.

y_i определяет ценность каждой дополнительной единицы дефицитного ресурса. Чем больше значение y_i, тем выше его приоритет при вложении дополнительных средств.

d) С помощью графического анализа чувственности определите, как изменится значение целевой функции при изменении максимального уровня производства продукта А на ±10 единиц.

1) x₁≤ 100 - 10 = 90

Необходимо найти максимальное значение целевой функции F = 20x₁+50x₂ → max, при системе ограничений:

2x₁+4x₂≤240, (1)

x₁≤90, (2)

-4x₁+40x₂≤0, (3)

x₁ ≥ 0, (4)

x₂ ≥ 0, (5)

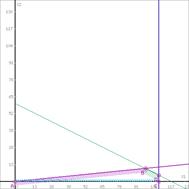
Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

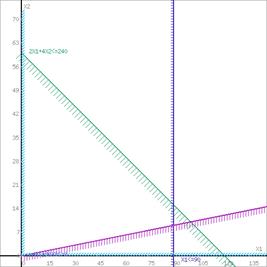
Или

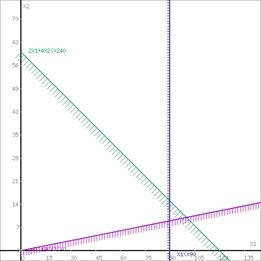
Шаг №2. Границы области допустимых решений.

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Обозначим границы области многоугольника решений.

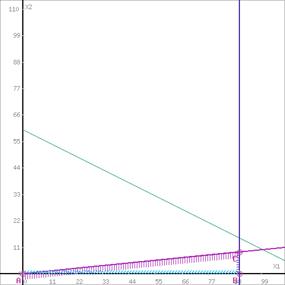
Шаг №3. Рассмотрим целевую функцию задачи F = 20x₁+50x₂ → max.

Построим прямую, отвечающую значению функции F = 20x₁+50x₂ = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (20;50). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

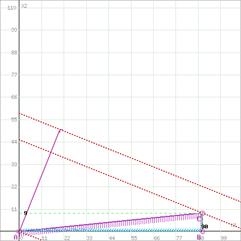
Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых:

x₁=90

-4x₁+40x₂=0

Решив систему уравнений, получим: x₁ = 90, x₂ = 9

Откуда найдем максимальное значение целевой функции:

F(X) = 20*90 + 50*9 = 2250

2) x₁≤100 + 10 = 110

Необходимо найти максимальное значение целевой функции F = 20x₁+50x₂ → max, при системе ограничений:

2x₁+4x₂≤240, (1)

x₁≤110, (2)

-4x₁+40x₂≤0, (3)

x₁ ≥ 0, (4)

x₂ ≥ 0, (5)

Шаг №1. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

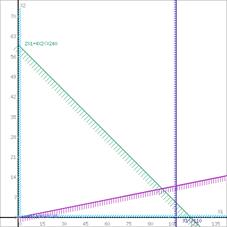
Или

Шаг №2. Границы области допустимых решений.

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Обозначим границы области многоугольника решений.

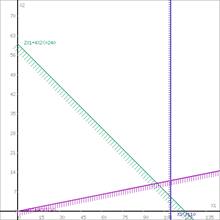
Шаг №3. Рассмотрим целевую функцию задачи F = 20x₁+50x₂ → max.

Построим прямую, отвечающую значению функции F = 20x₁+50x₂ = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (20;50). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

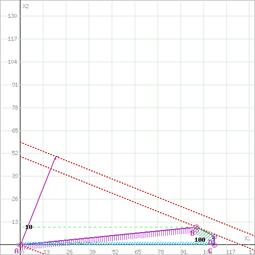
Прямая F(x) = const пересекает область в точке B. Так как точка B получена в результате пересечения прямых (1) и (3), то ее координаты удовлетворяют уравнениям этих прямых:

2x₁+4x₂=240

-4x₁+40x₂=0

Решив систему уравнений, получим: x₁ = 100, x₂ = 10

Откуда найдем максимальное значение целевой функции:

F(X) = 20*100 + 50*10 = 2500

Вывод: С помощью графического анализа чувственности определили, что значение целевой функции при изменении максимального уровня производства продукта А на +10 единиц не изменяется, а при изменении максимального уровня производства продукта А на -10 единиц уменьшается на 250.

Можно сделать вывод,  что не следует изменять план производства, т.к. на данный момент план самый оптимальный.