Система подготовки к ОГЭ по математике

 Система подготовки к сдаче ОГЭ по математике по теме «Уравнения»:

1.     Линейные уравнения:

1. Решите уравнение .

Решение. 

 Ответ: −4,5.

 2. Решите уравнение 

Решение. Умножим левую и правую часть уравнения на 4, получаем:

Ответ: −20.

3. Решите уравнение: 

Решение. 

Ответ: 6,3.

4. Решите уравнение: 

Решение. Последовательно получаем:

Ответ: 36.

5. Решите уравнение 

Решение. 

Ответ: −1.

6. Решите уравнение 

Решение. 

Ответ: −3.

7. Решите уравнение 

Решение. 

Ответ: 4.

8. При каком значении x значения выражений  и  равны?

Решение. Составим уравнение  

Решим его:

Ответ: 2.

9. Решите уравнение 

Решение. 

Ответ: 9,7.

10. Решите уравнение 

Решение. 

Ответ: 1.

2.      Квадратные уравнения:

1. Найдите корни уравнения . Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение. 

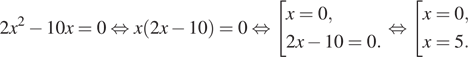
Ответ: 05.

2. Решите уравнение . Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение. По теореме, обратной теореме Виета, сумма корней равна 1, а их произведение −6.

Тем самым, это числа −2 и 3.

Ответ: −23.

3. Решите уравнение . Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение. Запишем уравнение в виде  По теореме, обратной теореме Виета, сумма корней равна −3, а их произведение −4.

Тем самым это числа −4 и 1.

Ответ: −41.

4. Решите уравнение . Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение. Запишем уравнение в виде  По теореме, обратной теореме Виета, сумма корней равна 2, а их произведение −8.

Тем самым это числа −2 и 4.

Ответ: −24.

5. Найдите корни уравнения  Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение. Запишем уравнение в виде:

По теореме Виета, сумма корней равна 5, а их произведение равно 4. Тем самым, это числа 4 и 1.

Ответ: 14.

6. Уравнение  имеет корни −6; 4. Найдите 

Решение. По теореме Виета 

Ответ: −24.

7. Квадратный трёхчлен разложен на множители:  Найдите 

Решение. Корни уравнения   — суть числа −9 и 3. В силу формулы  где  и   — корни уравнения  получаем  

Следовательно,  

Ответ: 3.

8. Решите уравнение 

Решение. Последовательно получаем:

Ответ: −9,7.

9. Решите уравнение 

Решение. Раскроем скобки и преобразуем выражение:

Ответ: 2,25.

10. Решите уравнение 

Решение. Квадраты чисел равны, если числа равны или противоположны:

Ответ: −2,5.

Приведем другое решение.

Раскроем скобки в обеих частях уравнения:

3.     Рациональные уравнения:

1. Решите уравнение 

Решение. Используем свойство пропорции:

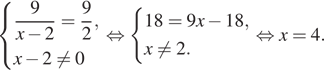
Ответ: 4.

2. Решите уравнение 

Решение. Используем свойство пропорции:

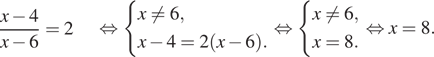
Ответ: 8.

3. Решите уравнение:  .

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение. Используем свойство пропорции.

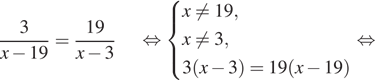
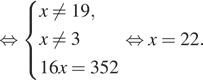
Ответ: 22.

Решите самостоятельно:

1.        Решите уравнение 

2.        Решите уравнение 

3.        Решите уравнение 

4.       Решите уравнение 

5.       Решите уравнение 

6.      Решите уравнение 

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

7.      Найдите корень уравнения 

8.       Уравнение  имеет корни −5; 7. Найдите 

9.      Решите уравнение 

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

10.   Решите уравнение 

Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Ответы для самопроверки:

1.       Ответ: 7.

2.       Ответ: −1,75.

3.       Ответ: −4.

4.       Ответ: 16

5.       Ответ: 1,5.

6.      Ответ: 06.

7.      Ответ: −1.

8.      Ответ: −35.

9.      Ответ: −3,6−2.

10.   Ответ: −32.