
Вычисления в таблицах выполняются с помощью формул. Формула может состоять из математических операторов, значений, ссылок на ячейку и функций. Результат выполнения формулы есть некоторое новое значение, содержащееся в ячейке, где находится формула.
Формула начинается со знака равенства "=".
В формуле могут использоваться следующие операторы:
- арифметические
+ сложение
- вычитание
* умножение
/ деление
^ возведение в степень
- сравнения
= равно
> больше
>= больше или равно
< меньше
<= меньше или равно
Порядок вычислений определяется обычными математическими законами.
Примеры:
Пусть в ячейке А4 содержится число 15
в ячейке В8 – число 20
в ячейке С6 – число 17
тогда формула (15+20)*17 будет иметь вид =(А4+В8)*С6
формула ![]() будет иметь вид = A4^4+C6/2
будет иметь вид = A4^4+C6/2
формула ![]() будет иметь вид = С6^ (1/5)+A4^(1/2)
будет иметь вид = С6^ (1/5)+A4^(1/2)
Основные понятия и правила записи функций
Для облегчения расчетов в табличном процессоре Excel есть встроенные функции.
Каждая стандартная встроенная функция имеет свое имя.
Для удобства выбора и обращения к ним, все функции объединены в группы, называемые категориями: математические, статистические, финансовые, функции даты и времени, логические, текстовые и т.д.
Использование всех функций в формулах происходит по совершенно одинаковым правилам:
- Каждая функция имеет свое неповторимое (уникальное) имя;
- При обращении к функции после ее имени в круглых скобках указывается список аргументов, разделенных точкой с запятой;
- Ввод функции в ячейку надо начинать со знака «=», а затем указать ее имя.
Рассмотрим наиболее часто встречающиеся функции по категориям:
1. Математические
|
Имя функции |
Название функции |
Пример записи в MS Excel |
Привычная запись примера, если значения в ячейках следующие: А1=-20; А2=12; А3=8; В1=30; В2=2; С1=3; С2=5; D1=7; D2=9 |
|
СТЕПЕНЬ(число; степень) |
Возведение в степень |
=СТЕПЕНЬ(5;3)
=СТЕПЕНЬ(6;(1/3))
=СТЕПЕНЬ(8;(2/5)) |
= 53 = = |
|
КОРЕНЬ(число) |
Значение квадратного корня |
= КОРЕНЬ(9) |
= |
|
ABS(число) |
Модуль (абсолютная величина) числа |
=ABS(-20) |
= |
|
SIN(число) |
Синус угла |
= SIN(5) |
= Sin 5 |
|
COS(число) |
Косинус угла |
= COS(30) |
= Сos 30 |
|
TAN(число) |
Тангенс угла |
= TAN(30) |
=Tg 30 |
|
ПИ( ) |
Значение числа p, округленного до 15 знаков после запятой (3,14159265358979) |
= ПИ( )
=SIN(2*ПИ()) |
=3,14159265358979 =Sin 2π |
|
LOG(число; основание) |
Логарифм числа по заданному основанию |
= LOG(30;4) |
= |
|
LOG10(число) |
Десятичный логарифм числа |
= LOG10(5) |
= lg 5 |
|
LN(число) |
Натуральный логарифм числа |
= LN(30) |
= ln 30
|
|
Имя функции |
Название функции |
Пример записи в MS Excel |
Привычная запись примера, если А1=-20; А2=12; А3=8; В1=30; В2=2; С1=3; С2=5; D1=7; D2=9 |
|
EXP(число) |
Экспонента числа |
= EXP(5)
= EXP(2^3)
|
= =
|
|
СУММ(число1; число2; …) |
Суммирование аргументов |
СУММ(А1;В1) |
= -20+30 суммирует значения из ячеек А1 и В1 |
|
СУММ(А1:А3) |
= -20+12+8 суммирует значения смежных ячеек, находящихся в диапазоне от А1 до А3 |
||
|
ПРОИЗВЕД(число1; число2; …) |
Произведение аргументов |
=ПРОИЗВЕД (А1;В1) |
= -20*30 умножает значения из ячеек А1 и В1 |
|
=ПРОИЗВЕД (А1:А3) |
= -20*12*8 умножает значения смежных ячеек, находящихся в диапазоне от А1 до А3 |
||
|
МОБР(массив) |
Обратной матрицы |
= МОБР(А1:В2) |
= |
|
МОПРЕД(массив) |
Определитель матрицы |
= МОПРЕД (А1:В2) |
= |
|
МУМНОЖ(массив1; массив2) |
Произведение матриц |
=МУМНОЖ(А1:В2;С1:D2) |
= |
При работе с матрицами необходимо учесть, что количество строк и столбцов должно быть одинаковым.
2. Статистические
|
Имя функции |
Название функции |
Пример записи в MS Excel |
Результат вычисления при А1=-20; А2=12; А3=8; В1=30; В2=2; С1=3; С2=5; D1=7; D2=9 |
|
МАКС(число1; число2; …) |
Максимальное значение |
=МАКС(-2;13;2) |
=13 |
|
МИН(число1; число2; …) |
Минимальное значение |
=МИН(5;-3;1) |
=-3 |
|
СРЗНАЧ(число1; число2; …) |
Среднее арифметическое |
=СРЗНАЧ(3;8;7) |
=6 |
|
СЧЕТ(значение1; значение2;…) |
Количество ячеек, содержащих числа |
=СЧЕТ(А1:А3) |
=3 |
Пример №1:
Вычислить значения У (х) = Sin(x-6) * Tg(x2) - Cos5x для всех х из отрезка [-3;8] с шагом h = 1,5
Полученные значения У(х) округлить до тысячных.
Решение: Оформить таблицу по образцу (рис.1.1.)

Рис.1.1. Образец заполнения таблицы
В ячейку С1 ввести формулу от руки и протянуть (скопировать) в соседние ячейки за маркер заполнения.
В
ячейку В2 ввести формулу с помощью Мастера функций, нажав кнопку ![]() и скопировать в
соседние ячейки.
и скопировать в
соседние ячейки.
Отформатировать ячейки для значений У(х) так, чтобы числа округлились до сотых: - выделить диапазон ячеек С2:I2
- [Формат]à[Ячейки]à вкладка Число à установить
формат числовой с 3 знаками после запятой (рис.
1.2.).

Рис.1.2. Результат вычислений
Пример №2: Вычислить произведение матриц А и В, если
А =
![]() ; В =
; В = ![]()
Решение:
![]()
Рис.1.3. Образец заполнения таблиц
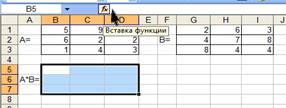
Рис.1.4. Образец выделения
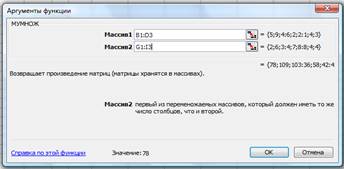
Рис.1.5. Образец ввода формулы при помощи Мастера функций
4. Нажать F2 и затем комбинацию клавиш Ctrl+Shift+Enter
5. В выделенном диапазоне ячеек появится результат произведения матриц (рис.1.6.)
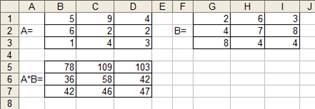
Рис.1.6. Результат нахождения произведения матриц
Пример №3: Вычислить обратную матрицу А-1 для матрицы
А = ![]()
Решение:
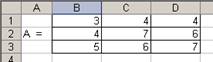
Рис.1.7. Образец заполнения таблицы
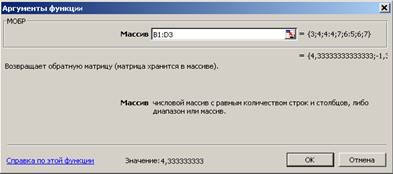
Рис.1.8. Образец ввода формулы при помощи Мастера функций
4. Нажать F2 и затем комбинацию клавиш Ctrl+Shift+Enter
5. В выделенном диапазоне ячеек появится обратная матрица (рис.1.9.)
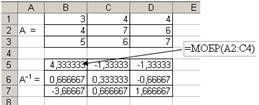
Рис.1.9. Результат нахождения обратной матрицы
6. Если формула не будет введена как формула массива, то в ячейке В5 будет выведено единственное значение.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.