Спирали фундирования в структуре проектирования сложных конструктов математического знания

Спирали фундирования в структуре проектирования сложных конструктов математического знания

Основной проблемой в математическом образовании в настоящее время выступает низкая учебная мотивация учащихся, что связано с тем, что в процессе обучения математике  учащиеся не достигают нужного уровня понимания основных математических понятий.

Преодолеть разобщенность знаний по отдельным темам и разделам курса математики возможно лишь на основе выделения наиболее существенных элементов, то есть за счет генерализации знаний.

Как отмечают ученые (А.Н. Колмогоров, М.Н. Скаткин и др.) такими элементами в математике являются математические конструкты, которые подразделяются на порядковые, алгебраические и топологические.

Изучение основных математических конструктов при традиционном изложении с трудом дается учащимся. Обобщающие и объединяющие понятия могут появляться в обучении как итоги изучения, а не как исходные пункты. В результате количественные изменения в мышлении у школьников происходят постоянно, а качественные скачкообразно, в отдельные периоды. На основании этого необходимо выделение ступеней развития, что является необходимым условием правильного подхода к отбору содержания обучения, то есть построения обучения по принципу «спирали» [25, с.51].

Существенные преимущества спиральной структуры знаний заключаются в том, что материал располагается в виде развертывающейся спирали, где каждый цикл образует целостную тему.

Последовательное содержание материала соотносится с определенными уровнями восприятия учебного материала, которые в дидактике называют уровнями усвоения.

Спиралевидное построение содержания обучения математике строится на базе концепции фундирования.

Спираль фундирования – это целостный интегрирующий механизм реализации преемственности для повышения качеств личности, расширения и углубления мыслительных способностей от школьных характеристик до профессиональных компетентностей будущего профессионала.

Как отмечает А.Н. Колмогоров, обучение математике в школе на основе фундирования строится в «естественном порядке наращивания знаний и умений» [12]. При этом автор считает, что «спираль» не обязательно разбивать на отдельные «витки».

А.А. Столяр предлагает четко различать уровни обучения, поэтому на базе ее подхода  каждый «виток» спирали следует соотносить с развитием определенного уровня мышления. Автор выделяет пять уровней сформированности внутренних структур мышления, которые развиваются в процессе поэтапности формирования знаний.

Концепция фундирования затрагивает не только построение содержания обучения, но направлена на формирование опыта и личностных качеств учащихся.

Данный способ планирования и организации учебного процесса с помощью развертывания через отдельные предметы дидактических спиралей фундирования имеет следующие характеристики:

-                   долгосрочный целевой ориентир на конечный результат обучения,

-                   осознание единства дисциплин с ориентацией на предпрофессиональную деятельность выпускников,

-                   крупноблочная организация учебного материала вместе с заданиями и рекомендациями по его изучению,

-                    открытость учебно-методических материалов для планирования и постановки вопросов и проблем на ближайшую перспективу.

Основная идея конструирования оснащенной спирали фундирования математического знания – это освоение математики на основе актуализации личностного опыта и творческого потенциала личности в процессе решения математических задач на основе не только наглядного моделирования, но и анализа обобщенного образца математической деятельности [1].

Оснащение спирали фундирования математических знаний можно представить в виде следующей схемы (рис.1).

Рисунок 1. Оснащение спирали фундирования математических знаний

Проектирование и реализация представленного рода спирали фундирования в процессе обучения эффективно, так как задает дополнительные ориентиры и интегративные конструкты в зонах актуального развития обучающихся. Развертывание таких спиралей охватывает активность обучающихся на всех этапах когнитивной деятельности, выделенных П.Я. Гальпериным, Н.Ф. Талызиной:

-                   ценностно-мотивационный;

-                   ориентировочный;

-                   исполнительский;

-                   контрольно-коррекционный.

Системообразующей базой, при фундировании выступает дидактический модуль, состоящий из нескольких фреймов.

Фрейм содержит опорную таблицу основных знаний, умений, навыков, методов и алгоритмов модуля. Основная функция фрейма заключается в содействии формирования внутренних устойчивых основ в процессе освоения содержания предмета.

Центральное место в модуле занимает фрейм аннотированной учебной программы, задающей объем учебной информации, требования к уровню усвоения каждого учебного элемента, образцы заданий для конкретики выдвигаемых требований [13].

Кроме того, в состав модуля входят фреймы базы данных спиралей фундирования, интегративной экзаменационной программы и историко-методического оснащения базовых учебных элементов.

Принцип фундирования, согласно В.В. Богун, можно адаптировать непосредственно при обучении определенной темы.

В  качестве примера использования фундирования рассмотрим процесс формирования понятия «величина», которое является составной частью не только математики, но и других наук.

Процесс освоения величины включает в себя ряд этапов [25]:

1 этап – дочисловой соответствует мышлению учащихся на уровне конкретных множеств; данная ступень фундирования характеризуется тем, что учащиеся выделяют разные свойства предметов, которые становятся в познании отделимыми, т.е. происходит формирование понятия об отношении порядка и рассмотреть  первоначальную порядковую структуру – упорядочивание множества; на этом этапе можно исходить из следующего самого общего, самого широкого определения величины: величинами одного рода называются элементы некоторого линейно упорядоченного множества.

2 этап связан с потребностью в уточнении понятия величины; на данном этапе числа отделяются от тех конкретных множеств, которые они характеризуют; алгебраические операции производят не над конкретными множествами предметов, а над числами; к этому этапу в формировании понятия о величине, к новому ее пониманию можно переходить после того, как ученики получат первоначальное представление о таких величинах, как длина, научатся складывать такие величины, выяснят смысл этой операции и ее свойства.

3 этап  - осуществляется переход от конкретных чисел, выражаемых цифрами, к абстрактным буквенным выражениям; в основу определения величины ложатся аксиомы упорядоченно группы, которые рассматриваются как  эмпирические свойства величины;

4 этап – связан с осуществлением «содержательной» аксиоматизации теории,  то есть теории в определенной конкретной ее интерпретации; в определении величины можно ввести дополнительную аксиому – условие непрерывности.

Самое важное при использовании концепции фундирования – это логическая завершенность.

Рассмотрим еще пример использования фундирования при обучении понятия предела функции. Понятие предела функции является начальным элементом спирали фундирования, базируясь на понятии предела числовой последовательности.

Понятие производной функции базируется на понятии предела функции, поскольку производная функции определяется как предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю, то есть в основе понятия производной как математического объекта лежит понятие объекта предела функции, которое выражается в виде следующего равенства:

Необходимо отметить, что при исследовании функций с целью построения их графиков используются как понятия пределов функций на бесконечности (нахождение уравнений горизонтальных асимптот) и в точках (нахождение уравнений вертикальных и наклонных асимптот), так и производных функций в точках (нахождение первой производной с целью определения критических точек и интервалов возрастания и убывания функции, а также второй производной с целью определения точек перегиба и интервалов выпуклости и вогнутости функции).

Понятие интеграла функции или объекта, называемого первообразной

функцией, базируется на понятии объекта производной функции, поскольку

нахождение неопределенного интеграла или первообразной функции определяется как операция, обратная нахождению производной функции, что отражено в виде следующей записи, тогда как производная функция, согласно утверждению выше, основывается на понятии предела функции:

Понятие дифференциального уравнения базируется на понятиях производной и интеграла функции, так как в записи дифференциального уравнения присутствуют производные определенных порядков.

 При решении дифференциального уравнения в общем или частном виде получаем соответственно несколько или одну интегральную кривую, которая определяется при нахождении соответствующего неопределенного интеграла с константой или точным числовым значением в итоге.

Применение принципа фундирования к исследованию функций вещественного переменного позволяет объединить следующие основные объекты в единую последовательную цепочку, которая позволяет сформировать представленную на рисунке 2 спираль фундирования.

Спираль фундирования объектов функций вещественного переменного

подразумевает определенное наследование статических (признаки или атрибуты) и динамических свойств (действий, операций) рассматриваемых объектов.

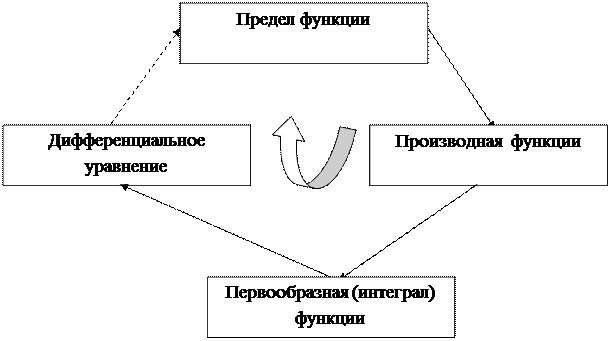Рисунок 2 – Спираль фундирования понятий функций вещественного переменного

Представим краткий сравнительный анализ элементарных арифметических операций, свойственных понятиям или объектам, рассматриваемых в рамках указанной спирали фундирования при исследовании функций вещественного переменного.

В частности, для пределов производных и первообразных функций вещественного переменного операции сложения, вычитания и умножения на число логически идентичное для данных объектов, тогда как операции умножения и деления в чистом виде выполняются только для пределов функций, для производных функций возникает абсолютно новая логическая формулировка данных операций, тогда как для интегралов она вообще отсутствует в чистом виде и заменяется методами замены переменной и интегрирования по частям. Необходимо отметить, что для дифференциальных уравнений как таковых наличие данных свойств не предполагается, однако при решении дифференциальных уравнений возникают первообразные и производные функции как необходимые компоненты.

В итоге, существенные преимущества спиральной структуры знаний заключаются в том, что материал располагается в виде развертывающейся спирали, где каждый цикл образует целостную тему. Основная идея конструирования оснащенной спирали фундирования математического знания – это освоение математики на основе актуализации личностного опыта и творческого потенциала личности в процессе решения математических задач на основе не только наглядного моделирования, но и анализа обобщенного образца математической деятельности. Применение принципа фундирования при рассмотрении основных понятий, связанных с исследованием функции вещественного переменного (пределы, производные и первообразные функции, а также дифференциальные уравнения), позволяет выявить определенную логическую зависимость между данными понятиями и провести их сравнительный анализ.

Скачано с www.znanio.ru