Анализ, геометрия и топология

УДК 514.765+517.938

О сепаратрисах одной динамической системы вблизи особой точки линейно нулевого типа

Абиев Н.А., Турткулбаева З.О.

Таразский государственный университет им. М.Х. Дулати abievn@mail.ru, zamira9091@mail.ru

Аннотация

В настоящей заметке предлагается приближенный метод построения сепаратрис на примере одной динамической системы, возникающей в задачах римановой геометрии.

Ключевые слова: динамическая система, особая точка, поток Риччи, обобщенное пространство Уоллаха

Введение

Цель настоящей заметки — приближенное построение сепаратрис следующей динамической системы вблизи единственной ее особой точки линейно нулевого типа:

                                                                          ,                                                   (1)

где

.

Система (1) получается при a1 = a2 = a3 = 1/4, x1 := x + 1, x2 := y + 1 из следующей системы, полученной в работах [1] – [3] при изучении нормализованных потоков Риччи на обобщенных пространствах Уоллаха:

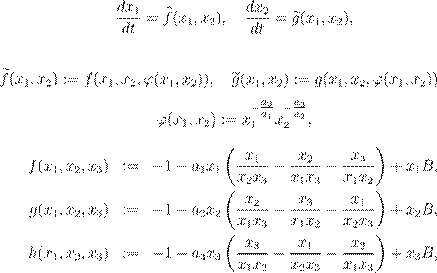(2)

где

,

 ,

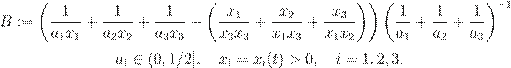Отметим, что исследования по потокам Риччи впервые были начаты в работе [12]. Соответствующий обзор дальнейших работ приведен в [9], [23]). Различные аспекты вопроса о свойствах потоков Риччи на однородных пространствах освещены в работах [4], [7], [8], [11], [13], [16], [21]. Читателям, интересующимся геометрическими аспектами исследуемой задачи, рекомендуем обратиться к работам [5], [6], [15], [17]–[20], [22], [24].

1             Предварительные сведения

малой окрестности произвольной точкиe 1 2 1 2 , где , и, следовательно, Очевидно, что в (2) функции f(x ,x ) и g(x ,x ) являются аналитическими в достаточно имеют место следующие представления:

,

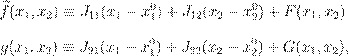где J11, J12, J21 и J22e— элементы матрицы Якоби (матрицы линейных частей)

 ,

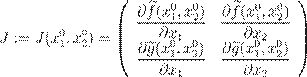F, G – некоторые функции, аналитические в окрестности  такие, что

.

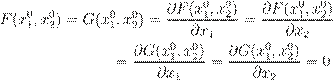Точка  называется особой для системы (1), если . Со-

гласно терминологии [10] особая точка  называется точкой линейно нулевого типа,e   e

если — нулевая матрица.

Опираясь на результаты работы [14], в работе [1] была доказана следующая теорема.

Теорема 1. Для системы (2) случай J = 0 может иметь место только при a1 = a2 = a3 = 1/4 с единственной особой точкой , являющейся седлом с шестью гиперболическими секторами (cм. рис. 1).

Отметим, что случай a1 = a2 = a3 = 1/4 соответствует пространству.

2             Построение сепаратрисы вблизи особой точки

Для системы (1) покажем приближенный метод построения сепаратрис гиперболических секторов, упомянутых в теореме 1. Известно, что нахождение сепаратрис нелинейных систем в общем случае является достаточно сложной задачей. Предлагаемая здесь идея

Рисунок 1. Фазовый портрет системы (2) в окрестности особой точки (1,1)

состоит в том, что в тейлоровских разложениях аналитических функций мы ограничиваемся членами до второго порядка включительно

,

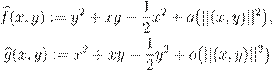и вместо (1) рассматриваем укороченную” систему

”

                                                         .                                      (3)

Такой подход оправдывает себя тем, что согласно нашим исследованиям в достаточно малой окрестности особой точки (0,0) системы (1) и (3) имеют одинаковые фазовые портреты.

Замена переменных y = xw (раздутие) приводит (3) к системе

                                .                   (4)

где C — произвольное действительное число. На рисунке 2 приведен фазовый портрет системы (4), где ясно выступают ее особые точки (седла) (0,−2), (0,−1/2), (0,1), соответствующие единственной особой точке (0,0) системы (3) согласно свойствам метода раздутия.

На рисунке 3 показаны сепаратрисы раздутой системы (4), соответствующие значению C = 0.008.

Из (5) легко получить первый интеграл системы (3):

                                                                              (y − x)(2y + x)(y + 2x) = C.                                                      (6)

Ясно, что уравнением (6) задается искомая кривая, которая разделяет интегральные линии (3), принадлежащие разным гиперболическим секторам вокруг точки (0,0). Например, при C = 0 в качестве таких сепаратрис мы получаем прямые линии y = x, y = −2x и y = −x/2. На рисунке 4 показаны сепаратрисы системы (3), соответствующие значению C = 0.005.

Рисунок 2. Фазовый портрет системы (4) в окрестности особых точек (0,−2), (0,−1/2),

(0,1)

Рисунок 3. Сепаратрисы системы (4), соответствующие значению C = 0.008

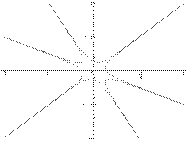
Рисунок 4. Сепаратрисы системы (3), соответствующие значению C = 0.005

Библиографический список

1.        Abiev N.A., Arvanitoyeorgos A., Nikonorov Yu.G., Siasos P. The dynamics of the Ricci flow on generalized Wallach spaces // Differential Geometry and its Applications. (2014), V. 35. P. 26–43.

2.        Abiev N.A., Arvanitoyeorgos A., Nikonorov Yu.G., Siasos P. The Ricci flow on some generalized Wallach spaces // Geometry and its Applications. Springer Proceedings in Mathematics. Switzerland: Springer. (2014), V. 72. P.3–37.

3.        Абиев Н.А., Арванитойоргос А., Никоноров Ю.Г., Сиасос П. Нормализованный поток Риччи на обобщенных пpостранствах Уоллаха // Математический форум. Т. 8. Часть 1. Исследования по математическому анализу. Владикавказ: ЮМИ ВНЦ РАН и РСО-А. (2014), 298 c. С.25–42.

4.        Anastassiou S., Chrysikos I. The Ricci flow approach to homogeneous Einstein metrics onflag manifolds // J. Geom. Phys. (2011), V. 61, No. 8, P. 1587–1600.

5.        Arvanitoyeorgos A. New invariant Einstein metrics on generalized flag manifolds // Trans.Amer. Math. Soc. (1993), V. 337, No. 2, P. 981–995.

6.        Besse A.L. Einstein Manifolds. Springer-Verlag. Berlin, etc., 1987.

7.        Bo¨hm C., Wilking B. Nonnegatively curved manifolds with finite fundamental groups admit metrics with positive Ricci curvature // GAFA Geom. Func. Anal. (2007), V. 17, P. 665–681.

8.        Buzano M. Ricci flow on homogeneous spaces with two isotropy summands // Ann. Glob. Anal. Geom. (2014), V. 45, No. 1, P. 25–45.

9.        Chow B., Knopf D. The Ricci Flow: an Introduction. Mathematical Surveys andMonographs, AMS, Providence, RI, 2004.

10.    Dumortier F., Llibre J., Artes J. Qualitative theory of planar differential systems.Universitext. Springer-Verlag, Berlin, 2006. xvi+298 pp.

11.    Glickenstein D., Payne T.L. Ricci flow on three-dimensional, unimodular metric Liealgebras // Comm. Anal. Geom. (2010), V. 18, No. 5, P. 927–961.

12.    Hamilton R.S. Three-manifolds with positive Ricci curvature // J. Differential Geom.(1982), V. 17, P. 255–306.

13.    Isenberg J., Jackson M., Lu P. Ricci flow on locally homogeneous closed 4-manifolds //Comm. Anal. Geom. (2006), V. 14, No. 2, P. 345–386.

14.    Jiang Q., Llibre J. Qualitative classification of singular points // Qual. Theory Dyn. Syst. (2005), V. 6, No. 1, P. 87–167.

15.    Kimura M. Homogeneous Einstein metrics on certain Ka¨hler C-spaces // Adv. Stud. Pure Math. (1990), V. 18, No. 1, P. 303–320.

16.    Lauret J. Ricci flow on homogeneous manifolds // Math. Z. (2013), V. 274, No. 1-2, P. 373–403.

17.    Lomshakov A.M., Nikonorov Yu.G., Firsov E.V. On invariant Einstein metrics on threelocally-symmetric spaces // Doklady Mathematics (2002), V. 66, No. 2, P. 224–227.

18.    Lomshakov A.M., Nikonorov Yu.G., Firsov E.V. Invariant Einstein Metrics on ThreeLocally-Symmetric Spaces // Matem. tr. (2003), V. 6, No. 2. P. 80–101 (Russian); English translation in: Siberian Adv. Math. (2004), V. 14, No. 3, P. 43–62.

19.    Nikonorov Yu.G., Rodionov E.D., Slavskii V.V. Geometry of homogeneous Riemannianmanifolds // Journal of Mathematical Sciences (New York) (2007), V. 146, No. 7, P. 6313– 6390.

20.    Nikonorov Yu.G. On a class of homogeneous compact Einstein manifolds // Sibirsk. Mat.Zh. (2000), V. 41, No. 1, P. 200–205 (Russian); English translation in: Siberian Math. J.

(2000), V. 41, No. 1, P. 168–172.

21.    Payne T.L. The Ricci flow for nilmanifolds // J. Mod. Dyn. (2010), V. 4, No. 1, P. 65–90.

22.    Rodionov E.D. Einstein metrics on even-dimensional homogeneous spaces admittinga homogeneous Riemannian metric of positive sectional curvature // Sibirsk. Mat. Zh. (1991), V. 32, No. 3, P.126–131 (Russian); English translation in: Siberian Math. J. (1991), V. 32, No. 3, P. 455–459.

23.    Topping P. Lectures on the Ricci flow, London Mathematical Society Lecture Note Series,

V. 325, Cambridge University Press, Cambridge, (2006).

24.    Wallach N. Compact homogeneous Riemannian manifolds with strictly positive curvature // Annals of Mathematics, Second Series. (1972), V. 96, P. 277–295.