Статья на тему: Изготовление моделей правильных многогранников

Изготовление моделей правильных многогранников

Цель работы: Закрепить понятие правильных многогранников, при изготовлении моделей, используя развертки.     

Приём  «До-После»

Вывод.

Я прав (не прав), так как ...

Описание: прием из технологии развития критического мышления

Использован на 1 этапе занятия как прием активизации учащихся, а также на этапе рефлексии.

Формирует:

·         умение прогнозировать события;

·         умение соотносить известные и неизвестные факты;

·         умение выражать свои мысли;

·         умение сравнивать и делать вывод.

В таблице заполняется часть "До", в которой студент записывает свои предположения, может записать гипотезу.

Часть "После" заполняется в конце занятия, когда изучен новый материал.

Далее студент сравнивает содержание "До" и "После" и делает вывод.

Теоретические сведения к  работе:

Выпуклый многогранник называется правильным, если его гранями являются равные правильные многоугольники, и все многогранные углы равны.

Рассмотрим возможные правильные многогранники и прежде всего те из них, гранями которых являются правильные треугольники. Наиболее простым таким правильным многогранником является треугольная пирамида, гранями которой являются правильные треугольники (рис. слева). В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также правильным тетраэдром, или просто тетраэдром, что в переводе с греческого языка означает четырехгранник.

Многогранник, гранями которого являются правильные треугольники, и в каждой вершине сходится четыре грани, изображен на рисунке посередине. Его поверхность состоит из восьми правильных треугольников, поэтому он называется октаэдром.

Многогранник, в каждой вершине которого сходится пять правильных треугольников, изображен на рисунке справа. Его поверхность состоит из двадцати правильных треугольников, поэтому он называется икосаэдром.

Заметим, что поскольку в вершинах выпуклого многогранника, не может сходиться более пяти правильных треугольников, то других правильных многогранников, гранями которых являются правильные треугольники, не существует.

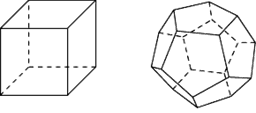Аналогично, поскольку в вершинах выпуклого многогранника может сходиться только три квадрата, то, кроме куба (рис. слева), других правильных многогранников, у которых гранями являются квадраты, не существует. Куб имеет шесть граней и поэтому называется также гексаэдром.

Многогранник, гранями которого являются правильные пятиугольники, и в каждой вершине сходится три грани, изображен на рисунке справа. Его поверхность состоит из двенадцати правильных пятиугольников, поэтому он называется додекаэдром.

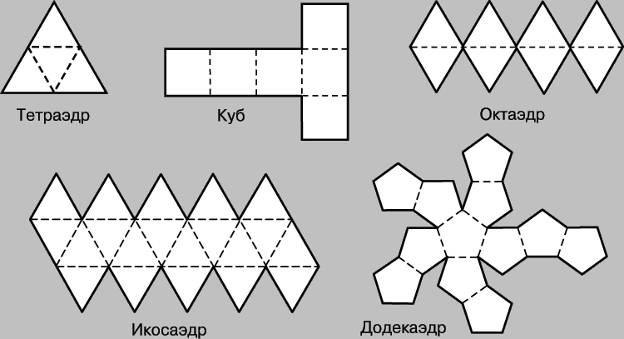
Одним из способов изготовления правильных многогранников является способ с использованием, так называемых,  развёрток.

Если модель поверхности многогранника изготовлена из гибкого нерастяжимого материала (бумаги, тонкого картона и т. п.), то эту модель можно разрезать по нескольким рёбрам и развернуть так, что она превратится в модель некоторого многоугольника. Этот многоугольник называют развёрткой поверхности многогранника. Для получения модели многогранника удобно сначала изготовить развёртку его поверхности.  При этом необходимыми инструментами являются клей и ножницы. Мо­дели многогранников можно сделать, поль­зуясь одной разверткой, на которой будут расположены все грани. Однако в этом случае все грани будут одного цвета.

Задания для самостоятельного решения:

Изготовьте модели правильных многогранников по их разверткам :

Заполните таблицу: