Статья "Полувековой опыт работы знаменитого Учителя и Методиста А.П.Киселёва"

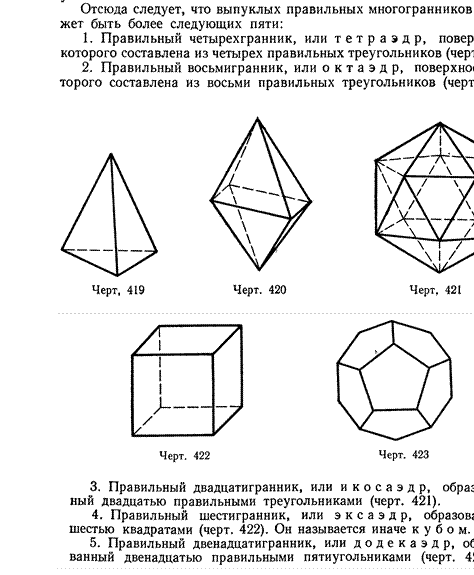
А. П. Киселев – это эпоха в педагогике и преподавании математики в средней школе. Его учебники математики установили рекорд долговечности, оставаясь свыше 60 лет самыми стабильными учебниками в отечественной школе, и на многие десятилетия определили уровень математической подготовки нескольких поколений граждан нашей страны.

Много лет назад Киселёв А.В. решил методические проблемы, которые   и сейчас        стоят перед          учителями.

 Главное его достижение в методике преподавания математики заключается в умеренной конкретизации и психологически правильном построении фраз, когда они не только верно отражают суть, а учитывают ход мысли ученика и направляют ее. И надо было изрядно помучиться в многолетнем решении методической задачи, чтобы оценить искусство А. П. Киселева. Очень незаметное, очень тонкое и редкостное педагогическое искусство. Редкостное! Современным ученым педагогам и авторам коммерческих учебников следовало бы заняться исследованиями учебников учителя гимназии А. П. Киселева.

Призыв "вернуться к Киселеву" раздается вот уже 30 лет.  Все новые учебники ориентированы на Науку, а точнее, на наукообразие и полностью игнорируют ученика, психологию его восприятия, которую умели учитывать старые учебники. Именно "высокий теоретический уровень" современных учебников — коренная причина катастрофического падения качества обучени и знаний. 

Сегодня усваивают математику около 20% учащихся (геометрию — 1%).

В 40-х годах полноценно усваивали все разделы математики

80%           школьников,           учившихся           "по           Киселеву". 

 Хороший учебник не "пишется" в один-два года по заказу министерства или для конкурса. Он не будет "написан" даже в десять лет. Он вырабатывается талантливым педагогом-практиком вместе с учащимися в течение всей педагогической жизни (а не профессором математики или академиком за письменным столом).

Именно так в течение более сорока лет (первое издание в 1884

г.) создавал свои замечательные, уникальные учебники учитель Воронежского реального училища А. П. Киселев. Его высшей целью было понимание предмета учащимися. И он знал, как эта цель достигается. Поэтому так легко было учиться по его книгам.  Свои педагогические принципы А. П. Киселев выразил очень кратко: "Автор... прежде всего ставил себе целью достигнуть трех качеств хорошегоучебника: точности (!) в формулировке и установлении понятий, простоты (!) в рассуждениях и сжатости (!) в изложении".

 Глубокая педагогическая значительность этих слов как-то теряется за их простотой. Но эти простые слова стоят тысяч современных диссертаций. 

Современные авторы, стремятся "к более строгому с логической стороны построению школьного курса математики" . 

Киселев заботился не о "строгости", а о точности (!) формулировок, которая обеспечивает их правильное понимание, адекватное науке. 

Точность — это соответствие смыслу. 

Пресловутая формальная "строгость" ведет к отдалению от смысла     и,       в конце          концов,       полностью уничтожает          его.

            Киселев даже не употребляет слова "логика" и говорит не о "логичных доказательствах", вроде бы неотъемлемо свойственных математике, а о "простых рассуждениях". В них, в этих "рассуждениях", разумеется, присутствует логика, но она занимает подчиненное положение и служит педагогической цели

— понятности и убедительности (!) рассуждений для учащегося.

 Наконец, сжатость. Обратите внимание, — не краткость, а сжатость! Краткость предполагает сокращение, выбрасывание чего-то, может быть, и существенного. Сжатость — сжимание без потерь. Отсекается только лишнее, — отвлекающее, засоряющее, мешающее сосредоточению на смыслах. Цель краткости — уменьшение объема. Цель сжатости — чистота сути! 

Еще одна тайна чудесной педагогический силы Киселева в том, что он не только психологически правильно подает каждую тему, но строит свои учебники (от младших классов к старшим) и выбирает методы соответственно возрастным формам мышления и возможностям понимания детей, неторопливо и основательно развивая их. Высший уровень педагогического мышления, недоступный современным дипломированным методистам и преуспевающим авторам учебников.

 А. М. Абрамов один из реформаторов-70, участвовал в написании "Геометрии" Колмогорова.Сделал вывод о том что только после многолетнего изучения и анализа учебников Киселева стал немного понимать скрытые педагогические "тайны" этих книг и "глубочайшую педагогическую культуру" их автора.

Не только в России, а также и в школах Израиля все это время пользуются учебниками Киселева. И пока мы эксперементируем с новыми учебниками по математике. 

Израильтяне обучали алгебре по нашему хрестоматийному Киселеву." 

 Классическое обучение "по Киселеву" предполагало изучение тригонометрических функций и аппарата их преобразований в виде отдельной дисциплины в 10 классе, а в конце — приложение усвоенного к решению треугольников и к решению стереометрических задач. Последние темы были замечательно методически проработаны с помощью последовательности типовых задач. Стереометрическая задача "по геометрии с применением тригонометрии" была обязательным элементом выпускных экзаменов на аттестат зрелости. Учащиеся хорошо справлялись с этими задачами. 

А сегодня? Абитуриенты МГУ не могут решить простую планиметрическую задачу!

 Некоторым кажется, что у Киселёва есть ошибки. Но это же не ошибки, это сознательные, педагогически оправданные пропуски, облегчающие понимание. Это — классический методический принцип русской педагогики: "не следует стремиться сразу к строго логическому обоснованию того или иного математического факта. Для школы вполне приемлемы "логические скачки через интуицию", обеспечивающие необходимую доступность учебного материала"   Модернизаторы-70 заменили этот принцип антипедагогическим псевдонаучным принципом "строгого" изложения. Именно он уничтожил методику, породил непонимание и отвращение учащихся к математике. 

Приведу пример педагогических уродств, к которым ведет этот принцип.

 Во многих современных учебниках даны сложные, тяжеловесные, незапоминающиеся определения,когда в научном отношении все верно, а в педагогическом — вопиющая безграмотность. Это определение напечатано жирным шрифтом, значит, для обязательного заучивания, и занимает полстраницы. Так разве суть школьной математики в том, чтобы миллионы школьников зубрили определения в полстраницы учебника? В то время, как у Киселева это определение дано для выпуклого многогранника и занимает менее двух строк. Это и научно, и педагогически грамотно."

Из учебника Киселева Элементарная геометрия

Еще один интересный неожиданно приоткрывший одну поистине "тайну" Киселевских книг. На вопрос: Какое отношение у вас к учебникам Киселева? Чаще всего от учителей математиков звучит такой ответ: "Учебники хорошие, но они устарели". Но вот если рассмотреть на примере чертёж Киселева к признаку параллельности двух плоскостей. На этом чертеже плоскости резко изгибаются для того, чтобы пересечься. 

И когда смотришь на этот чертёж сразу же возникает чёткая формулировка: "Если две пересекающиеся прямые "одной плоскости параллельны -..", а вслед за ней и все короткое доказательство "от противного".

 Наконец, пример непревзойденного искусства Киселева сравнительно с современными авторами. Например, современные действующие учебники для 9-го класса "Алгебра-9", Автор — Ю. Н. Макарычев , и между прочим, именно учебники Макарычева, а также Виленкина, приводятся в качестве примера "недоброкачественных, ... безграмотно выполненных" Л. С. Понтрягин . Первые страницы: §1.

"Функция. Область определения и область значений функции".

 В заголовке указана цель — разъяснить ученику три взаимосвязанных математических понятия. Как же решается эта педагогическая задача? Вначале даются формальные определения, потом множество разношерстных абстрактных примеров, затем множество хаотичных упражнений, не имеющих рациональной педагогической цели. На лицо перегрузка и абстрактность. Изложение занимает семь страниц. Форма изложения, когда начинают с невесть откуда взявшихся "строгих" определений и затем "иллюстрируют" их примерами, трафаретна для современных научных монографий и статей.

 Сравним изложение той же темы А. П. Киселевым (Алгебра, ч. 2. М.: Учпедгиз. 1957). Методика обратная. Начинается тема с двух примеров — бытового и геометрического, эти примеры хорошо знакомы ученику. Примеры подаются так, что естественно приводят к понятиям переменной величины, аргумента и функции. После этого даются определения и еще 4 примера с очень краткими пояснениями, их цель — проверить понимание ученика, придать ему уверенности. Последние примеры тоже близки ученику, они взяты из геометрии и школьной физики. Изложение занимает две (!) страницы. Ни перегрузки, ни абстрактности! Это яркий пример "психологического изложения".

 Показательно сравнение объемов книг. Учебник Макарычева для 9 класса содержит 270 страниц . Учебник Киселева содержит 224 страницы, но рассчитан на три года обучения — для 8-10 классов.

                    Объем              увеличился              в              три              раза!

 Сегодня очередные реформаторы стремятся уменьшить перегрузку и "гуманизировать" обучение, якобы заботясь о здоровье школьников.

Слова, слова... 

На самом же деле, вместо того, чтобы сделать математику понятной, они уничтожают ее основное содержание. Сначала, в 70-х гг. "подняли теоретический уровень", подорвав психику детей, а теперь "опускают" этот уровень примитивным методом выбрасывания "ненужных" разделов (логарифмы, геометрия и др.) и сокращением учебных часов .А это вызывает пробелы в целостности математических знаний и ограниченность в применении терии к практике.

Изучение математики требует от каждого ученика больших усилий и немалого времени. Полученные при этом навыки учебного труда позволяют выпускникам школы в их дальнейшем жизненном пути эффективно овладевать навыками выполнения других видов труда и с должным пониманием относиться к тому, что хорошее выполнение любой работы требует значительных усилий и ответственности.

При правильно поставленном обучении у учащихся развиваются наблюдательность, внимание и сосредоточенность, инициатива и настойчивость, понимание важности коллективного труда и уважение к труду своих товарищей. Все это имеет большое значение для нравственного воспитания учащихся, формирования их характера.

Изучение математики дает учащимся правильное диалектико- материалистическое понимание вопросов происхождения и развития математических понятий и методов. Учащиеся получают представление о месте математики в системе наук и ее роли в современном обществе, в развитии науки, техники, производства.

Привлекаемые в процессе обучения факты из истории математики и из современной жизни в доступной для учащихся форме позволяют раскрыть материалистическую основу происхождения научных знаний, на ярких примерах показать познаваемость явлений окружающего мира. Тем самым изучение математики содействует пониманию закономерностей мира, развивает интерес учащихся к приобретению научного взгляда на процессы развития природы и общественной жизни, подготавливает к сознательному овладению мировоззренческими вопросами при изучении обществоведения и вносит свой вклад в формирование. марксистско-ленинского мировоззрения учащихся.

К примеру из книги Киселева 

Параллельные плоскости