
МБОУ СОШ №95 г. Воронежа, учитель математики
(2014г.)
Одним из важнейших показателей высокого уровня математического развития учащихся является умение решать нестандартные геометрические задачи. Целью современной школы является вооружение учеников различными методами и способами решения задач, а также обучение их самостоятельному поиску решения.
В исследованиях психологов, дидактов, методистов в последнее время ярко показано, что количество решенных задач не свидетельствует о наличии у школьников четко сформированного умения их решать.
В математике существуют такие приемы, которые могут облегчит сам поиск решения. Эти приемы не зависят от того, к какому типу или разделу относится та или иная задача, поэтому данные приемы получили название единых приемов целенаправленного поиска решения любых задач. Это так называемые эвристические приемы.
Что же такое эвристика? Нетрудно догадаться, что в основе слова лежит другое, более знакомое и близкое нам ещё по школьной легенде об Архимеде, когда ликующий и возбужденный своим внезапным открытием Архимед воскликнул: "Эврика! Эврика!", что значило: "Нашел! Нашел!" Да, эвристические приёмы решения задач в значительной степени именно помогают найти их решение.
В своей книге "Как решать задачу?" известный американский математик Д. Пойа так пишет об эвристике: "Эвристика - так называлась не совсем чётко очерченная область исследования, относимая то к логике, то к философии, то к психологии. Она часто охарактеризовывалась в общих чертах, редко излагалась детально и по существу предана забвению в настоящее время». Цель эвристики - исследовать методы и правила, как делать открытия и изобретения? Наиболее известные попытки создать стройную систему эвристики принадлежат Ренэ Декарту и Лейбницу. Декарт имел намерение разработать универсальный метод решения задач. Однако его "Правила для направления ума" остались неоконченными. Лейбниц также намеревался написать "Искусство изобретения", но не осуществил своего намерения. Интересное и подробное изложение эвристики оставил Бернард Больцано "Эвристика ставит себе целью установить общие закономерности тех процессов, которые имеют место при решении всякого рода проблем, независимо от их содержания". / Пойа / Прилагательное "эвристический", значит "служащий для открытия".
Процесс решения геометрической задачи в основном соответствует принципу решения любой задачи, который включает в себя такие основные моменты, как:
1) анализ задачи;
2) схематическая запись задачи;
3) поиск способа решения;
4) осуществление решения задачи;
5) проверка решения;
6) исследование задачи;
7) формулирование ответа задачи;
8) анализ решения;
Одним из популярных средств для поиска решения задачи является аналогия. Аналогия - сходство предметов в каких-либо свойственных признаках и отношениях, причем таких предметов, которые различны. Действия по аналогии таковы: на основе того , что два предмета имеют общие признаки , и установлено , что первый из них имеет ещё некоторый признак X наличие которого у второго предмета пока не известно , делается предположение (гипотеза) , что второму предмету , по видимому тоже присущ признак X.
Схема умозаключения по аналогии выглядит так.
Первая посылка: предмет А обладает признаками a , b , c , x.
Вторая посылка: предмет В обладает признаками a , b , c.
Заключение: предмет В, вероятно, тоже обладает признаком X.
Таким образом, умозаключения по аналогии являются умозаключениями правдоподобными; для того, чтобы выяснить достоверность или ложность “вывода по аналогии” необходимо дополнительно исследовать этот вывод.
Рассмотрим следующую задачу.
Задача№1. Зная стороны a , b , c в ΔABC вычислить радиус r вписанной в него окружности.
Решим вспомогательную задачу.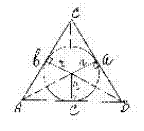 1. Соединим центр
О вписанной окружности с вершинами ΔABC
1. Соединим центр
О вписанной окружности с вершинами ΔABC
2. SΔABC=SΔAOB+SΔAOC+SΔBOC
3. ПустьS-площадь ΔABC. По формуле
Герона S=![]() , где p-полупериметр
ΔABC
, где p-полупериметр
ΔABC
4. SΔAOB=![]() , SΔAOС=
, SΔAOС=![]() и т.д.
и т.д.
5. Тогда S=![]() (a+b+c)r=рr, откуда r=
(a+b+c)r=рr, откуда r=![]()
Решаем исходную задачу, проводя аналогичные рассуждения
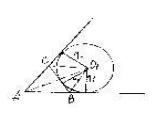 1. Соединим центр
О1 окружности с вершинами ΔABC
1. Соединим центр
О1 окружности с вершинами ΔABC
2. SΔАВС=SΔAO1B+SΔAO1C-SΔBO1C
3. если S-площадь ΔABC,тоS= p(p-a)(p-b)(p-c)
4. SΔAO1B=![]() , SΔAO1С=
, SΔAO1С=![]() , SΔBO1C=
, SΔBO1C=![]()
5. (2)= >S=![]() (b+c-a)r1. Замечая,что p-a=
(b+c-a)r1. Замечая,что p-a=![]() (b+c-a)-a=
(b+c-a)-a=![]()
получим следующий
вывод:S=(p-a)r1, откуда r1=![]()
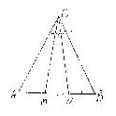 Предположим, что
данное утверждение верно, т.е. ÐACM=ÐMCN, тогда ΔACN- равнобедренный,
и CM в нём – высота. С
другой стороны при предположении о равенстве углов MCB и NCB мы получаем, что
треугольник MCB- равнобедренный,
и CN- высота, таким
образом мы имеем в ΔABC две высоты, проведенные из одной вершины
С,
Предположим, что
данное утверждение верно, т.е. ÐACM=ÐMCN, тогда ΔACN- равнобедренный,
и CM в нём – высота. С
другой стороны при предположении о равенстве углов MCB и NCB мы получаем, что
треугольник MCB- равнобедренный,
и CN- высота, таким
образом мы имеем в ΔABC две высоты, проведенные из одной вершины
С,
что невозможно. Поэтому наше предположение о равенстве данных трех углов не имеет места.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Ответ: нет.
Ответ: нет.
Задача №3. Определить радиус окружности,
описанной около равнобедренного треугольника , если основание и боковая сторона
треугольника соответственно равны 6см и 5см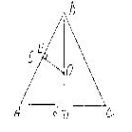 .
.
Решение.
Чертеж по условию и требованию задачи
позволяет выдвинуть предположение о том, что радиус ОВ целесообразно искать,
исходя из подобия прямоугольных треугольников АВD и ОВЕ (ÐОВЕ- общий), т.к. ΔОВЕ ~ ΔАВС, то ![]() , откуда: 1) ОВ=
, откуда: 1) ОВ=![]() , где ВЕ и ВD неизвестны;
, где ВЕ и ВD неизвестны;
2)ВЕ=![]() , где АВ - известно; ВЕ=2,5см
, где АВ - известно; ВЕ=2,5см
3) ВD=![]()
4) АD=![]() АС
АС
5) АD=![]()
Ответ: 3![]()
Задача №4. В
равнобедренной трапеции АВСД основания АД и ВС равны соответственно а
и b (а>b). Точка М
является серединой АД, а точка N делит боковую сторону СД в отношение ![]() =K. Найти высоту трапеции, если
прямые СМ и ВN взаимно
перпендикулярны.
=K. Найти высоту трапеции, если
прямые СМ и ВN взаимно
перпендикулярны.
Решение
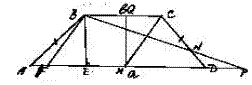 Продолжим BN и AD до пересечения в
точке P, через т. P проведём прямую BF параллельно CM.
Продолжим BN и AD до пересечения в
точке P, через т. P проведём прямую BF параллельно CM.
1.
Т.к.
по условию BN![]() CM, то ∆PBF прямоугольный.
Его высота BE совпадает с
высотой трапеции.
CM, то ∆PBF прямоугольный.
Его высота BE совпадает с
высотой трапеции.
2.
Найдём
отрезки EF и EP, которые являются
проекциями катетов треугольника PBF на гипотенузу. Пусть Q – середина BC. Имеем MF=BC=b, EM=BQ=![]() . Отсюда получаем FE=MF-EM=
. Отсюда получаем FE=MF-EM=![]() . Далее EP=EM+MD+DP=
. Далее EP=EM+MD+DP=![]() +DP
+DP
3.
Из
подобия ∆BNC и ∆PND находим DP=BC×![]() =kb, таким образом EP=
=kb, таким образом EP=![]() +kb.
+kb.
4.
Зная
проекции катетов на гипотенузу, по известной. формуле найдем высоту: BE=![]() =
= ![]()
![]() .Продолжим BN и AD до пересечения в
точке P, через т. P проведём прямую BF параллельно CM.
.Продолжим BN и AD до пересечения в
точке P, через т. P проведём прямую BF параллельно CM.
5.
Т.к.
по условию BN![]() CM, то ∆PBF- прямоугольный.
Его высота BE совпадает с
высотой трапеции. Найдём отрезки EF и EP, которые являются
проекциями катетов треугольника PBF на гипотенузу. Пусть Q – середина BC. Имеем MF=BC=b, EM=BQ=
CM, то ∆PBF- прямоугольный.
Его высота BE совпадает с
высотой трапеции. Найдём отрезки EF и EP, которые являются
проекциями катетов треугольника PBF на гипотенузу. Пусть Q – середина BC. Имеем MF=BC=b, EM=BQ=![]() . Отсюда получаем FE=MF-EM=
. Отсюда получаем FE=MF-EM=![]() . Далее EP=EM+MD+DP=
. Далее EP=EM+MD+DP=![]() +D .Из подобия ∆BNC и ∆PND находим DP=BC×
+D .Из подобия ∆BNC и ∆PND находим DP=BC×![]() =kb, таким образом EP=
=kb, таким образом EP=![]() +kb.
+kb.
6.
Зная
проекции катетов на гипотенузу, по известной. формуле найдем высоту: BE=![]() =
= ![]()
![]() .
.
Ответ:
![]()
![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.