Статья не тему "Математика на уроках физики"

Елена Николаевна Щанова

учитель физики

МБОУ «Средняя школа № 3 города Няндома»

г. Няндома

Архангельская обл.

Математика на уроках физики

Краткая аннотация

В статье рассказывается о том, что математика часто используется в физике и в определённой мере определяет ход физического образования.  Суть физических процессов можно изучать на основе доступных школьникам понятий математики. Одновременно это обеспечивает повышение уровня математической подготовки. К тому же учащиеся видят, что абстрактные математические формулы и понятия имеют реальное воплощение в физических процессах.

Ключевые слова: математика, физика, формулы, физические процессы, преобразования.

Большое место при изучении различных разделов физики, начиная с 7 класса, отводится решению задач. Это одно из важнейших средств развития мыслительных и творческих способностей учащихся, это средство формирования ряда практических умений и навыков, это способ проверки уровня понимания и осмысления изученного материала.

Большинство физических задач требует проведения определенных расчетов, вычислений для получения конечного результата. Часто задача бывает правильно оформлена, решена в общем виде с применением физических формул, но ребята испытывают трудность в проведении расчетов. Поэтому, начиная с 7 класса, я рекомендую использовать на уроках физики самые простые микрокалькуляторы. Обычно к этому времени обучающиеся уже имеют навыки работы с калькулятором: выполняют простейшие операции сложения, вычитания, деления, умножения, возведения в квадрат, извлечение квадратного корня. Все это, безусловно, упрощает процесс решения задач.

К 7 классу для успешной работы на уроках физики у обучающихся должны быть сформированы навыки всех арифметических действий с целыми числами, обыкновенными и десятичными дробями. Нахождение общего знаменателя, дополнительного множителя при действии с дробями, правила приближенного вычисления и округления чисел – часто вызывают у ребят затруднения.

На первых уроках в 7 классе мы выполняем лабораторную работу «Определение размеров малых тел», где знакомим обучающихся с методом рядов.[2] Одно из заданий заключается в том, что нужно определить размер молекулы на фотографии и ее истинный размер при увеличении в 70000 раз. Сложным для ребят оказалось проведение такого расчета:

   = 0,0000357 мм

Вызывает затруднения деление и умножение на число, меньше единицы.

Например:    4 : 0, 0002       или     5,4 · 0,001

При изучении темы «Механическое движение» обучающиеся должны иметь понятие об использовании буквенных обозначений, о прямой и обратной пропорциональности, уметь выражать искомую величину из данной формулы. Особенно плохо ребята справляются с теми задачами, где требуется провести математическое преобразование, и даже самые простейшие преобразования у некоторых ребят вызывают затруднения.

Например:

S - путь             V - скорость          t – время

V=           Выразить                S -  ?        t - ?

Ребята легко запоминают единицы измерения физических величин, но перевод дольных и кратных единиц в основные (системы СИ) вызывает у них затруднение.

Проблемы возникают при переводе значения скорости из   в   .

Например:  36  = 36   = 10  

Задача №1.[1]

 В течении 30 с поезд двигался равномерно со скоростью 72 км/ч. Какой путь прошел поезд за это время?

В этой задаче время дано в секундах, значит скорость нужно представить в м/с.

V = 72  =  = 20

S = V· t            S = 20 · 30 с = 600 м

В процессе изучения этой темы мы уже работаем с графиками пути S(t)  и скорости  V(t) для равномерного движения, т.е. обучающиеся должны уметь определять по графику абсциссу и ординату точки в прямоугольной системе координат, уметь изображать точку по заданным координатам и строить графики прямой пропорциональности.

Задача №2.[2]

На рисунке изображен график пути равномерного движения. На графике OS – ось пройденных путей, Ot – ось времени. Найти по графику путь, пройденный телом за 10 часов и скорость движения.

Решение:                                                           S, км

t =  10 ч                S = 500 км                   500

                                                                       0             10

При изучении темы «Плотность вещества» необходимо знать:

1)                единицы измерения массы тела и соотношения между ними;

Например: Выполняя лабораторную работу «Измерение массы тела на рычажных весах»[2] ребята испытывают трудности при переводе единиц массы:

m = 52 г 300 мг = 52,3 г = 0,0523 кг

2)                способы вычисления  площади и объема тела, единицы измерения этих величин и соотношения между ними;

S = a b – площадь прямоугольника

V = a b c – объем прямоугольного параллелепипеда

V = S h – объем цилиндра

S =  - площадь круга

l = 2πr – длина окружности

Задача №3.[2]

Машина рассчитана на перевозку груза массой 3 тонны. Сколько листов железа можно на нее погрузить, если длина каждого листа 2 м, ширина 80 см, толщина 2 мм?

Дано:                      СИ                      Решение:

a = 2 м                                        1)     V = a b c

b = 80 см                0,8 м                 V = 2 м· 0,8 м · 0,002 м = 0,0032

с = 2 мм                 0,002 м         2)      m = ρ · V

ρ = 7800                               m = 7800  · 0,0032  = 25 кг

М = 3 т                   3000 кг        3)    N =

N - ?                                                N =  = 120

              Ответ: 120 листов.

Очень часто в условии задачи объем жидкости задан в литрах, поэтому нужно знать и уметь пользоваться соотношением:    1 м ³ = 1000 л       1 л = 0,001 м ³

Изучая понятие силы, мы уже в 7 классе делаем упор на то, что сила – векторная величина, которая характеризуется  не только модулем (числовым значением), но и направлением. Силу на чертеже изображают в виде направленного отрезка прямой со стрелкой на конце. Обучающиеся должны знать, что длина отрезка равна модулю силы в выбранном масштабе.

Задача №4.[2]

Мешок муки имеет массу 50 кг. Вычислите силу тяжести, действующую на мешок, и изобразите ее на рисунке.

Решение:

   = m g            = 50 кг·10  = 500 Н

Уже здесь применяется обозначение вектора, но вскользь,

не заостряя на этом внимания.

В конце 7 класса изучается вопрос о КПД простого механизма. Предполагается, что учащиеся должны знать понятие процента и его вычисление:

КПД =  ·100%               100% = 1           40% = 0,4

В 8 классе к перечисленным знаниям по математике добавляется умение работать с числом в степени, знать правила действия со степенями:

 = 10000             = 0, 0001

Задача № 1.[3]

Удельная теплота сгорания топлива q = 1, 4 ·  Дж / кг.  Какое количество теплоты выделится при полном сгорании 0,4 кг этого топлива?

Q = q·m            Q = 0,4 кг · 1, 4 ·  Дж / кг = 0,56 ·  Дж = 56 ·  Дж

Последнее преобразование числа обычно вызывает затруднение у ребят.

Задача № 2.[3]

Какая масса дров сгорела, если при этом выделилось 50 000 кДж энергии?

m =              m =  =  кг = 5 кг

При  решении задач на расчет общего количества теплоты необходимо производить сложение :

Q = Q1 + Q 2            Q = 6,8 ·  Дж + 8,4 · Дж = 15,2 ·  Дж

или   3,2 ·  Дж  + 82 000 Дж =  · ( 3,2 + 0,82) Дж = 4,02 · Дж

При изучении темы «Электризация тел» тоже приходится работать со степенями.

Задача № 3 .[3]

Какому числу электронов соответствует заряд электроскопа, равный – 6,4 ·  Кл?

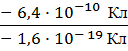N =             N =    = 4 ·

При изучении темы «Закон Ома для участка цепи» мы знакомимся с формулой I = U/R, где силу тока можно рассмотреть как функцию двух переменных. Установить функциональную зависимость между силой тока и одной из них можно лишь в том случае, если третья величина зафиксирована (например, R = const). При построении графика зависимости I(U) можно использовать тот же способ, что и в алгебре (с помощью таблицы, где U- аргумент, I- функция). Необходимо обратить внимание учащихся на сведения из курса математики:

1)                Так как между силой тока и напряжением зависимость прямая, то достаточно двух точек для построения графика зависимости силы тока от напряжения.

2)                Так как между силой тока и сопротивлением зависимость обратная, то двух точек уже недостаточно.

Следует напомнить, что если между двумя физическими величинами установлена функциональная зависимость, то ее можно задать тремя способами: формулой, таблицей и графиком.

В конце  8 класса при изучении темы «Световые явления» учащимся необходимо знать понятие угла, градусной меры углов, уметь пользоваться транспортиром и циркулем. Как видим, взаимосвязь физики с математикой настолько очевидна, что не говорить об этом нельзя.

В 9 классе самая сложная программа по физике за курс основной школы. Здесь изучается механика – раздел физики о движении и взаимодействии тел.[4]  Его можно назвать «математической физикой», так как основной упор делается на решение задач и учащимся не обойтись без соответствующей математической подготовки. Необходимо повторить следующие понятия: система координат, вектор, действия с векторами, умножение вектора на скаляр, правила сложения и вычитания векторов (правило треугольника и правило параллелограмма), проекция вектора на координатную ось.

Задача №1.[5]

В начальный момент времени тело находилось в точке с координатами xo = - 2 м,      yo = 4 м. Затем тело переместилось в точку с координатами x = 2 м, y = 1 м. Найти проекции вектора перемещения на ось x и y и модуль вектора перемещения.

 = x – xo                 = 2 м – (- 2 м) = 4 м

 = y – yo                = 1 м – 4 м = - 3 м

Эта задача предполагает знание теоремы Пифагора:

=  +         = 16 м² + 9 м² = 25 м²       S = 5 м

В процессе изучения физики в 9 классе широко пользуются такими математическими понятиями как функция, графики функции, т. е. устанавливают функциональную зависимость между физическими величинами. Известно, что формулировка любого физического закона имеет математическую форму, т.е. записывается в виде некоторой функциональной зависимости. Так для формулировки физических законов часто используются слова «прямо пропорционально» и «обратно пропорционально». Не все понимают смысл этих терминов. При изучении раздела механики «Кинематика» приходится иметь дело со следующими математическими функциями:

·        линейной функцией вида y = ax (например:  зависимость между перемещением и временем при равномерном движении S = V· t)

·        линейной функцией вида y = ax + b (зависимость скорости от времени при равноускоренном движении V = Vo + at )

·     квадратичной функцией вида y = a  (зависимость кинетической энергии от скорости при постоянной массе  = )

·     квадратичной функцией вида y = a  + bx (зависимость перемещения от времени при равноускоренном движении S = Vo t + / 2) [4]

Таким образом, суть физических процессов можно изучать на основе доступных школьникам понятий математики. Одновременно это обеспечивает повышение уровня математической подготовки. К тому же учащиеся видят, что абстрактные математические формулы и понятия имеют реальное воплощение в физических процессах.

В общеобразовательной школе изучение математики и естественных дисциплин происходит параллельно. Математика часто используется в физике и в определённой мере определяет ход физического образования. Преподавание физики и математики необходимо строить на взаимном использовании элементов математики в курсе физики и физических представлений при изучении алгебры и геометрии.

Список источников:

1.     В.И. Лукашик, Е.В. Иванова «Сборник задач по физике», Москва «Просвещение», 2005 г.

2.     А.В.Перышкин «Физика 7класс», учебник для общеобразовательных учреждений, Москва «Дрофа», 2009 г.

3.     А.В.Перышкин «Физика 8 класс», учебник для общеобразовательных учреждений, Москва «Дрофа», 2009 г.

4.     А.В.Перышкин, Е.М. Гутник «Физика 9 класс», учебник для общеобразовательных учреждений, Москва «Дрофа», 2009 г.

5.     А.П.Рымкевич «Сборник задач по физике», Москва «Просвещение», 2005 г.