Сценарий урока по геометрии за 8 класс по теме "Теорема Пифагора" по ФГОС

Сценарий урока по геометрии 8 класс. Теорема Пифагора.

Урок геометрии в 8 классе, УМК Атанасян Л.С.

Учитель математики МБОУ СОШ № 6 г. Воткинск, Тарасова Т.И.

Тема урока: Теорема Пифагора

Тип урока: урок изучения нового материала

Цели урока:

• Изучить теорему Пифагора, обеспечить ее усвоение всеми учащимися; сформировать умение вычислять неизвестные стороны в прямоугольном треугольнике;
• Через доказательство теоремы, решение задач, постановку дополнительных вопросов и заданий, развивать творческую и мыслительную деятельность учеников, их интеллектуальные качества – способность к «видению проблемы», самостоятельность, гибкость, учить объективно оценивать себя и корректировать свою деятельность в ходе урока;
• Прививать интерес к геометрии, воспитывать веру в свои силы, учить коллективной и самостоятельной работе.

•         Развитие творческих способностей учащихся

Структура урока:

• Мотивационно-организационный момент.
• Актуализация опорных знаний и подготовка учащихся к усвоению нового материала.
• Изучение нового материала.
• Первичная проверка усвоения знаний.
• Первичное закрепление знаний.
• Информация о домашнем задании
• Подведение итогов урока.

1.      Мотивационно-организационный момент

Добрый день, ребята! Наверное, вы немного уже устали? Повернитесь лицом друг к другу, улыбнитесь, прикоснитесь ладонью к соседу по парте, передав ему частицу своей доброты и хорошего настроения. А теперь присаживайтесь, и мы приступаем к серьезной работе.

2.      Актуализация опорных знаний и подготовка учащихся к усвоению нового материала Проверка домашнего задания. Ученикам было предложено решить 3 задачи (на выбор минимум нужно было решить 2 задачи). Решение задач проверяется со слайдом.

 Устный фронтальный  опрос.

Геометрическая разминка

1.       Какие виды треугольников вам известны? Сегодня мы будем общаться, в основном, с прямоугольным треугольником

2.       Какой треугольник называется прямоугольным?

3.       Как называются стороны прямоугольного треугольника?

4.       Какая сторона в треугольнике самая большая?

5.       Как сравнить длины катетов и гипотенузы?

6.       Как найти площадь прямоугольного треугольника?

7.       Сторона квадрата равна a см. Найдите его площадь

8.       Сторона квадрата равна a+b см. Найдите его площадь

   3.Изучение нового материала. Погружение в проблему.

Приближается наш самый любимый праздник Новый год. В канун этого праздника во многих семьях принято дарить подарки. И вот я решила своей маме подарить красивую вазу длиной 32 см. Конечно, любой подарок должен быть красиво упакован. В магазине мне предложили праздничную коробку, длина которой 30см, ширина 16 см, высота 10см. Помогите определить, поместиться ли ваза в данную коробку? Условие: примерить размеры вазы к коробке не разрешают.

Обучающиеся предлагают свои варианты решения проблемы.

Оказывается, дети, нам недостаточно знаний сегодня для реализации этой проблемы.

Значит, надо пополнить свои знания. Давайте совершим мини-экскурсию в историю геометрии. Посмотрите на портреты этих выдающихся людей. Вы с ними знакомы? Чем прославил геометрию Евклид? А Фалес? Не могли бы вы назвать имя последнего ученого?

Совершенно верно, это Пифагор. Так вот Пифагор, наверняка, поможет решить нам эту проблему.

Итак, давайте сформулируем тему и цели урока. Тема «Теорема Пифагора».

Цели урока:

1.      Познакомиться с теоремой Пифагора

2.      Доказать теорему Пифагора

3.      Научиться решать задачи с помощью теоремы Пифагора.

Что вы знаете о Пифагоре?

Немного  из биографии Пифагора (сообщения обучающихся)

Пифагор  родился в 576 г. до н.э. на острове Самос  Древней Греции.  Отец Пифагора, Мнесарх, был ювелиром. Он был достаточно богат, чтобы дать сыну хорошее воспитание. Пифагор — это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор это значит «убеждающий речью»).

Пифагор с ранних лет стремился узнать как можно больше. Он являлся первым выдающимся ученым, который утверждал, что явления природы можно объяснить математически, доказал математическую теорию музыки.

О жизни этого ученого известно немного, зато с его именем связано много легенд. В молодости он много  путешествовал по странам, побывал в  Египте и Вавилоне, где изучал разные науки.   Известно, что четыре раза подряд  Пифагор был олимпийским чемпионом. Вернувшись на родину основал свою философскую школу закрытого типа - пифагорейский союз. Богатую историю имеет теорема, носящая имя Пифагора.

Согласно легенде,  в честь своего  открытия Пифагор принес в жертву  сто быков.

А задавались ли Вы вопросом «Есть ли связь между сторонами прямоугольного треугольника? Если такая связь есть, то в чем она заключается?». Ответить на этот вопрос нам поможет следующая практическая работа, которую мы выполним, работая в группах (на группы учащиеся разделены по рядам, так как в кабинете столы не двигаются). У каждой группы на парте имеется инструкция работы, следуя которой мы получим великое открытие (у каждой группы лист формата А-3,  линейки, угольники, маркеры)

1)      Постройте прямоугольный треугольник с заданными катетами

Группа 1 a=3,b=4                          

Группа 2 a=6, b=8

Группа 3 a=5, b=12

2)      Найдите длину гипотенузы c

3)      Постройте на катетах и гипотенузе треугольника квадраты с заданной стороной.

4)      Найдите площади получившихся квадратов

5)      Сделайте выводы о соотношении площадей квадратов построенных на катетах и гипотенузе.

После выполнения практической работы представители от групп презентуют свою работу, сравнивая результаты приходим к выводу о том, что «Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на его катетах».

Еще со времен Пифагора известен, сей факт, который в древнем Вавилоне получен опытным путем, но не доказан. Пифагор доказал это соотношения и теорема стала носить его имя. Сегодня она звучит так «В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы».

Докажем эту теорему.

Существует около двух сотен доказательств этой теоремы, например доказательство Леонардо да Винчи, Евклида, Эпштейна, Нильсена, Королева, Ватта, Темпельгофа, Гарфилда, Хоукинса, Перигаля, Бхаскари- Агарна, Гутхейля и т.д.

Ученики, доказывая данную теорему, придумывали много разных баек вроде «Пифагоровы штаны во все стороны равны»

«Ослинный мост» данная теорема в средние века была по силам только сильным ученикам, а слабых называли ослами, а теорема для них была  что вроде «непреодолимым мостом» в школе Пифагора.

 А сейчас, давайте решим проблему урока.

Решение проблемы: Ваза длиной 32 см. поместится праздничную коробку, длина которой 30см, ширина 16 см, высота 10см.? Да.  с² = 30²+16²= 900+256=1156;  с = 34

4.Первичная проверка усвоения знаний. В раздаточных картах нужно выполнить

Задание №1

Запишите теорему Пифагора для каждого из треугольников, изображенных на рисунке, если это возможно

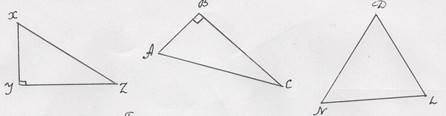
Задание №2

    В прямоугольном треугольнике a и b-катеты, c- гипотенуза.

1. Выразить c через a и b
2. Выразить a через b и c
3. Выразить b через a и с        

Задание №3

Вычислите, если возможно:

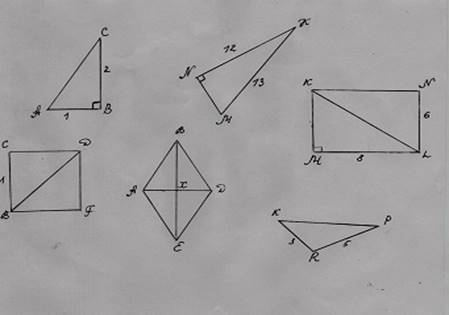
a)      Сторону АС   треугольника АВС

b)      Сторону MN   треугольника MNK

c)      Диагональ KL прямоугольника  KMLN

d)      Диагональ BD квадрата  BCDF

e)      Сторону АВ ромба  ABDE

f)       Сторону KP  треугольника KPR

5.Проверочная работа:

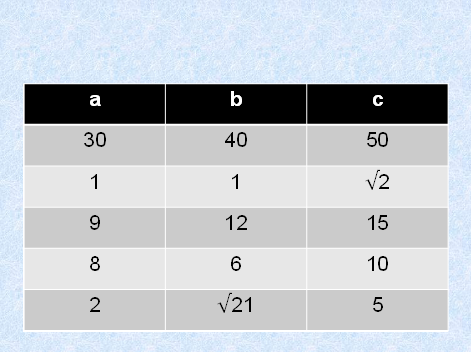
В прямоугольном треугольнике a и b катеты, c-гипотенуза. Заполните таблицу (таблица с заданием выдана каждому учащемуся в начале урока)

На выполнение задания отводиться 5минут, затем ученики меняются таблицей с соседом по парте, а учитель открывает на доске заполненную таблицу, осуществляют взаимопроверку и оценивание работы.

6. Запись и комментирование домашнего задания:

Задача: 1.  Найдите  высоту  CF трапеции ABCD, используя данные рисунка:

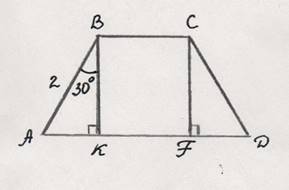
Творческое задание: Найти интересные доказательства теоремы Пифагора

К результату мы придем

7. Рефлексия - подведение итогов урока

Для рефлексии своей деятельности на уроке учащиеся заполняют таблицу, которую получили от учителя в начале урока

В заключении прочитаю шуточную  формулировку  теоремы Пифагора для её лучшего запоминания.

Если дан нам треугольник,

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим -

И таким простым путем

Проверка домашнего задания 42,43,44

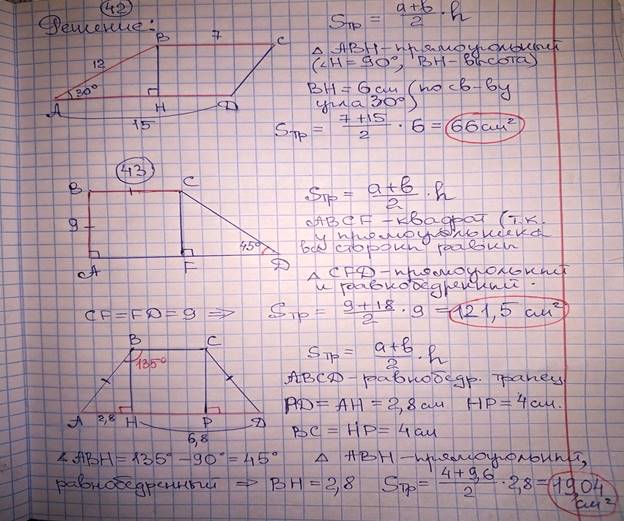
Проверочная работа