Сумма углов треугольника.

Конспект урока геометрии в  7 классе

Класс:

Дата:

Тема: сумма углов треугольника.

           Цель урока: познакомить учащихся с доказательством теоремы о сумме углов треугольника;

Задачи урока:

           1. обобщить знания свойств и признаков параллельных прямых, смежных и вертикальных углов;

2. развитие логического мышления, познавательного интереса, любознательности, умение анализировать, наблюдать и делать выводы;

 3. Воспитание культуры математической речи.

Ход урока.

I. Мотивационно-целевой этап

1. Организационный момент

Приветствую учеников, проверяю их готовность к уроку.

2. Актуализация опорных знаний. Постановка цели урока.

     На предыдущих уроках мы с вами изучали признаки и свойства параллельности прямых. И сегодня на уроке, полученные по этой теме знания, помогут сделать открытие. Фигура, с которой мы будем работать, вам уже знакома. Это треугольник.

Вопросы к  классу: Что мы о нем знаем? Сколько у треугольника вершин, углов, сторон?   Какие треугольники вы знаете? Чему равна сумма углов треугольника?

Итак, тема нашего урока «Сумма углов треугольника».

Цели нашего урока: сформулировать и доказать теорему о сумме углов треугольника; рассмотреть задачи на применение доказанной теоремы. (Слайд 2)

3. Актуализация опорных знаний.

Устная работа с задачами (Слайды 4 -9).

II. Процессуально - познавательный этап

1.              Изучение нового материала.

У вас на столах лежат треугольники из бумаги (остроугольные, тупоугольные, прямоугольные).

Используя модели треугольников, определить, какой угол получится, если его составить из углов треугольника. Чему равна его градусная мера? (Углы треугольников можно отрывать.)

Проверяя результаты измерений углов треугольников различного вида, практическая работа показала, что сумма углов любого треугольника равна 180°. Этот факт был установлен практически ещё в Древнем Египте. Теперь мы попытаемся доказать это утверждение. Теорема о сумме углов треугольника - это одна из самых важных теорем геометрии. (Слайды 10-11).

2.              Доказательство теоремы.

Теорема: Сумма углов треугольника равна 180° .(Слайд12-13).

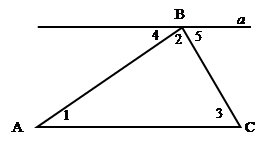
Дано: ΔАВС.

Доказать: А+В+С=180⁰.

Доказательство.

1.                 Проведем через т. В прямую а || АС.

2.         4=1 (накрест лежащие при а || АС и секущей АВ),

5= (накрест лежащие при а || АС и секущей ВС).

3.         5++=180⁰ – развернутый угол.

4.         Заменяя равные углы, получим: 1++=180⁰

5.         Или А+В+С=180⁰.

Обратите внимание на чертёж. Какой мы рассматривали треугольник (по углам)? Запомните, что у остроугольного треугольника все углы острые. Могут ли в треугольнике быть два прямых или два тупых угла и почему? (Слайд 14).

Теорема о сумме углов треугольника приписывается многим, в том числе Евклиду и Пифагору. Теорема Пифагора-Евклида многострадальная "твёрдо установленная", которая была подвергнута ревизии в неевклидовой геометрии. (Слайд 15, 16).

3.              Физкультминутка.

Раз - согнуться, разогнуться,

Два – нагнуться, подтянуться,

Три – в ладоши три хлопка,

Головою три кивка,

На четыре – руки шире,

На пять, шесть – тихо сесть

На семь, восемь – лень отбросим,

И продолжим наш урок. (Слайд 17).

4. Первичное закрепление материала.     

а). Решение задач на готовых чертежах. (Cлайды19-24).

б). Решение задач из учебника №225, № 228 (рассмотреть 2 случая) (Слайды 28-29.)

III. Рефлексивно-оценочный этап

1. Подведение итогов урока

Давайте вместе с Вами подведём итоги нашего урока.

·                   Какую мы сегодня изучали теорему?

·                   Было ли на уроке легко, интересно?

·                   Оцените своё настроение на уроке:

2. Рефлексия.

Выберите фразеологизм или пословицу которые характеризуют вашу  работу сегодня

Шевелить мозгами

Краем уха

Хлопать ушами

3. Оценка содержательного аспекта деятельности учащихся на уроке.

Выставление отметок за урок, их комментарий, высказывание замечаний учащимся.

          Домашнее задание: теория, § 30, 223(а, б), 228(в), №229 (по желанию)