
Технологическая карта урока
ФИО учителя: Надежда Валентиновна Такшеева
Класс: 8
Предмет: геометрия
Тема: «Площади фигур»
Тип урока: обобщение и систематизация знаний
Место урока в изучаемой теме: одиннадцатый урок темы
Цель: тренировка навыка использования новых и знакомых формул для решения задач на нахождение площадей при решении практических задач. Обобщение и систематизация знаний по теме: «Площади многоугольников».
Задачи:
1. Систематизировать учебный материал через осмысление связей и отношений в объектах изучения.
2. Развить умение анализировать, обобщать изученные факты, выделять и сравнивать существенные признаки, характерные для каждого вида плоских геометрических фигур.
3. Формировать личностные качества учащихся: настойчивость в достижении цели, заинтересованность в конечном результате труда.
Планируемые результаты
|
Предметные знания, предметные действия |
УУД |
|||
|
регулятивные |
познавательные |
коммуникативные |
личностные |
|
|
Владеют базовым понятийным аппаратом (площади фигур, плоские фигуры, многоугольник, параллелограмм, трапеция и т.п.), умеют работать с геометрическим текстом с использованием специальной терминологии; умеют использовать формулы для вычисления площадей плоских фигур, умеют устанавливать закономерность в применении формул; умеют использовать различные языки математики (словесный – символический – графический).
|
Принимают и сохраняют цели и задачи учебной деятельности; умеют выполнить взаимооценку и самооценку; · владеют навыком самоконтроля и взаимоконтроля.
|
Умеют принимать решения в условиях неполной и избыточной, точной и вероятностной информации, выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; · умеют выделять признаки объекта и на их основе проводить сравнение; умеют выделять главное, сравнивать, обобщать, проводить аналогию, применять индуктивные способы рассуждений; имеют представление о математике как средстве моделирования явлений окружающего мира. |
Учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; · умеют грамматически и логически правильно выражать свои мысли средствами как естественного, так и математического языков; умеют работать в паре, в группе; понимают смысл поставленной задачи, ясно и чётко излагают свои мысли в устной речи, выстраивают аргументацию, приводят примеры; |
Проявляют познавательный интерес через понимание простоты нахождения площади фигуры различными способами; · выражают потребность ставить перед собой цели и достигать их; осознают границы собственного знания-незнания; проявляют ценностно-эмоциональное отношение к изучаемому математическому содержанию с общекультурных позиций; имеют представление о значении математической науки как сфере человеческой деятельности |
Ход урока
|
|
Название этапа урока |
Задача, которая должна быть Решена (в рамках достижения планируемых результатов урока) |
Формы организации деятельности учащихся |
Действия учителя по организации деятельности учащихся |
Действия учащихся (предметные, познавательные, регулятивные) |
Результат взаимодействия учителя и учащихся по достижению планируемых результатов урока |
Диагностика достижения планируемых результатов урока |
|
1 |
Мотивационный |
Создать благоприятный психологический настрой на работу |
Фронтальная |
Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. |
Включаются в деловой ритм урока. |
|
Самоконтроль подготовленности к работе на уроке |
|
2 |
Актуализация опорных знаний и умений. |
Целеполагание, Планирование учебного сотрудничества с учителем и сверстником.
|
Фронтальная |
Предлагает рассмотреть фигуры на плакате (Приложение 1), Подводит к теме урока через фронтальную беседу Ответьте на вопросы: 1. Что общего у фигур, изображенных на плакате, что различного? 2. Как называются эти фигуры (общее название)? 3. Какие формулы фигур знаете? 4. Что будем изучать на уроке? 5. Какие есть предложения по планированию урока? |
1.Ученики узнают фигуры, называют формулы площадей многоугольников, отвечают на вопросы и называют тему урока, задачи урока. 2.Записывают цель урока в тетрадь, задачи урока - на доске.
|
Р.: Принимают и сохраняют цели и задачи учебной деятельности. Пр.: Владеют базовым понятийным аппаратом (площади фигур, плоские фигуры, многоугольник, параллелограмм, трапеция и т.п.), умеют работать с геометрическим текстом с использованием специальной терминологии. |
Запись задач урока на доске. |
|
3 |
Фиксирование индивидуального затруднения в пробном учебном действии. |
Выявление границ собственного знания - незнания |
Индивидуальная |
Дает задания: 1.Соотнести формулы с фигурами, закрепленными на доске (Приложение № 1). 2. Решить задачи на нахождение площади фигур (карточки Приложение 2). Каждый ряд выполняет свои задания. Каким правилом пользовались? Можно повторить его по учебнику. Составьте алгоритм решения заданий. |
1. Повторяют формулы на нахождение площадей фигур 2. Решают задачи на нахождение площади фигур. 3. Анализируют объекты с целью составления алгоритма решения задачи. 4.Работают самостоятельно, сверяются с решением у доски, исправляют, помогают друг другу. 5.Обсуждают решение задач на карточках . |
Л.: Осознают границы собственного знания-незнания. Р.: Принимают и сохраняют цели и задачи учебной деятельности; умеют выполнить взаимооценку и самооценку. Пр.: Умеют использовать формулы для вычисления площадей плоских фигур, умеют устанавливать закономерность в применении формул.
|
Алгоритм решения задач. Самопроверка способом сверки с образцом. |
|
4 |
Закрепление |
Выполнение пробного задания с использованием знакомых формул, но на новом материале. |
Работа в парах
|
Учитель раздает задания с чертежами плоских фигур (Приложение 3). (Давайте обсудим пути решения этих задач), инструктирует, направляет; Если отдельные учащиеся испытывают затруднения, учитель показывает способ решения.
|
1.Решают задачи на готовых чертежах на клетчатой бумаге. 2.Ученики в парах формулируют проблемы, строят логическую цепь рассуждений и находят способ решения. 3.После решения, обмениваются карточками, проверяют ответы.
|
К.: Учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. · К.: Умеют грамматически и логически правильно выражать свои мысли средствами как естественного, так и математического языков; умеют работать в паре, в группе. Пр.: Умеют устанавливать закономерность в применении формул. Р.: Взаимооценка. |
Взаимопроверка в парах. Проверка учителем.
|
|
5 |
Самостоятельная работа |
Тренировка навыка решения задач на нахождение площади фигуры, не имеющей своей формулы. |
Индивидуальная |
Учитель раздает задания для самостоятельной работы, инструктирует, направляет. Карточки (Приложение 4). |
1.Решают задачи на нахождение площадей многоугольников. 2.Ученики выполняют самостоятельную работу и сдают учителю. 3.Структурируют знания, выбирают наиболее эффективные способы решения задач. |
П.: Умеют использовать различные языки математики (словесный – символический – графический). Л.: Проявляют познавательный интерес через понимание простоты нахождения площади фигуры различными способами. |
Проверка учителя. |
|
6 |
Подведение итогов урока. |
Содержательная рефлексия (фронтальный опрос) |
Фронтальная |
Учитель задает вопросы: - Как найти площадь фигуры, не имеющей свою формулу? - Где в окружающей жизни может встретиться умение находить площадь фигуры? - Как применить формулу в новой, нестандартной ситуации? |
Отвечают на вопросы учителя, инициативное сотрудничество. |
П.: Умеют выделять главное, сравнивать, обобщать, проводить аналогию, применять индуктивные способы рассуждений; имеют представление о математике как средстве моделирования явлений окружающего мира. |
Устный опрос. |
|
7 |
Рефлексия. |
Осуществление обратной связи. |
Индивидуальная |
Предлагает оценить сегодняшний урок знаком «+», «-» или «+/-» : 1. «Научился применять формулы в нестандартной ситуации» 2. «Остались неясности, хочу задать вопрос __________» 3. «Все понятно, нужно потренироваться в решении практических задач » 4. «Ничего не понял, нужна дополнительная консультация» (Приложение 5». |
Заполняют листы обратной связи, задают вопросы. |
Самооценка . |
Листы обратной связи |
Приложение № 1
Повторение формул площадей многоугольников
Соотнести формулы с фигурами, закрепленными на доске.
|
I ряд |
II ряд |
III ряд |
|
S=
|
|
|
Приложение № 2
Устная работа (фронтальная)
Найти площади многоугольников (на карточках).
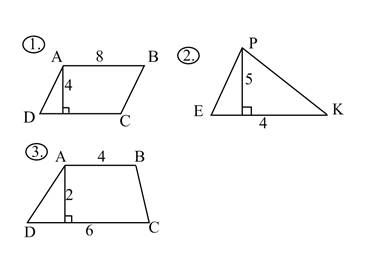
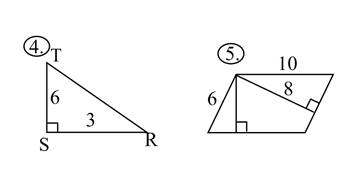
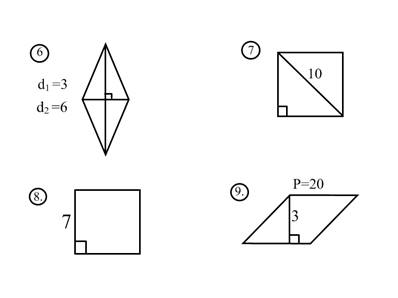
Приложение № 3
Работа в парах по нахождению площадей фигур
1. 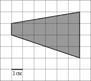 На
клетчатой бумаге с клетками размером 1 см
На
клетчатой бумаге с клетками размером 1 см ![]() 1 см
изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах
1 см
изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах
2. 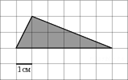 На
клетчатой бумаге с клетками размером 1 см
На
клетчатой бумаге с клетками размером 1 см ![]() 1 см
изображен треугольник (см. рисунок). Найдите его площадь в квадратных
сантиметрах. Ответ дайте в квадратных сантиметрах.
1 см
изображен треугольник (см. рисунок). Найдите его площадь в квадратных
сантиметрах. Ответ дайте в квадратных сантиметрах.
3. 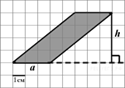 На
клетчатой бумаге с клетками размером 1 см
На
клетчатой бумаге с клетками размером 1 см ![]() 1 см
изображен параллелограмм (см. рисунок). Найдите его площадь в квадратных
сантиметрах.
1 см
изображен параллелограмм (см. рисунок). Найдите его площадь в квадратных
сантиметрах.
4.  На
клетчатой бумаге с клетками размером 1 см
На
клетчатой бумаге с клетками размером 1 см ![]() 1 см
изображен треугольник (см. рисунок). Найдите его площадь в квадратных
сантиметрах.
1 см
изображен треугольник (см. рисунок). Найдите его площадь в квадратных
сантиметрах.
5. 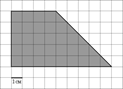 На
клетчатой бумаге с клетками размером 1 см
На
клетчатой бумаге с клетками размером 1 см
![]() 1 см
изображена трапеция (см. рисунок). Найдите ее площадь
1 см
изображена трапеция (см. рисунок). Найдите ее площадь
в квадратных сантиметрах.
6.  На
клетчатой бумаге с клетками размером 1 см
На
клетчатой бумаге с клетками размером 1 см ![]() 1 см
изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
1 см
изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
7.  На
клетчатой бумаге с клетками размером 1 см
На
клетчатой бумаге с клетками размером 1 см
![]() 1 см
изображена фигура (см. рисунок). Найдите ее площадь
1 см
изображена фигура (см. рисунок). Найдите ее площадь
в квадратных сантиметрах.
8. 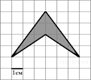 На
клетчатой бумаге с клетками размером 1 см
На
клетчатой бумаге с клетками размером 1 см ![]() 1 см
изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
1 см
изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
Заполнить таблицу
|
Номер задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Ответ |
|
|
|
|
|
|
|
|
Приложение № 4
Самостоятельная работа
|
I вариант |
II вариант |
|
1. Диагонали ромба 13 и 14. Найти его площадь. 2. Основание трапеции 7 и 8, а высота 4. Найти площадь трапеции. 3. Найти площадь треугольника, изображенного на рисунке.
4. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
5. В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45º. Найдите площадь трапеции.
|
1. Диагонали ромба 8 и 15. Найти его площадь. 2. Основание трапеции 2 и 15, а высота 7. Найти площадь трапеции. 3. Найти площадь треугольника, изображенного на рисунке.
4. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
5. В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45º. Найдите площадь трапеции.
|
Оцените сегодняшний урок знаком «+», «-» или «+/-»:
|
1. «Научился применять формулы в нестандартной ситуации» |
|
|
2. «Остались неясности, хочу задать вопрос __________» |
|
|
3. «Все понятно, нужно потренироваться в решении практических задач » |
|
|
4. «Ничего не понял, нужна дополнительная консультация» |
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.