Технологическая карта урока по математике в 5а классе ТЕМА: «ДЕСЯТИЧНЫЕ И ОБЫКНОВЕННЫЕ ДРОБИ» Иванова Зольфия Джавдетовна, учитель математики ГБОУ лицей №82 Петроградского района Санкт-Петербурга

Оценка 4.6

Документация

docx

математика

4 кл—5 кл

29.01.2024

Технологическая карта урока по математике в 5а классе ТЕМА: «ДЕСЯТИЧНЫЕ И ОБЫКНОВЕННЫЕ ДРОБИ» Иванова Зольфия Джавдетовна, учитель математики ГБОУ лицей №82 Петроградского района Санкт-Петербурга

Государственное бюджетное общеобразовательное учреждение

лицей №82 Петроградского района Санкт-Петербурга

Технологическая карта урока по математике в 5а классе

ТЕМА: «ДЕСЯТИЧНЫЕ И ОБЫКНОВЕННЫЕ ДРОБИ»

Иванова Зольфия Джавдетовна,

учитель математики

ГБОУ лицей №82 Петроградского района

Санкт-Петербурга

Санкт-Петербург

2023

Технологическая карта урока

Учитель: Иванова Зольфия Джавдетовна

Тип урока: Урок открытия нового знания (ОНЗ)

Тема: «Десятичные и обыкновенные дроби»

Класс: 5а класс

Учебник: : Математика 5 класс, учебник (в двух частях) для общеобразовательных учреждений , Л.Г. Петерсон, Г.В. Дорофеев.. – М.: БИНОМ. Лаборатория знаний, 2019г.

Программа: 1) Математика. Сборник рабочих программ.5–6 классы: пособие для учителей общеобразоват. учреждений / сост. Т.А. Бурмистрова -Москва: Просвещение, 2011г.

«Учусь учиться» по образовательной системе «Школа 2000…» Г.В. Дорофеева и Л.Г. Петерсон, Москва 2007 год

Дополнительные материалы: : интерактивная доска, проектор, компьютер, мультимедийная презентация с необходимыми заданиями, цветные карточки.

Цели урока:

Создать условия для пробного проектирования жизненной и профессиональной карьеры на основе соотнесения своих интересов, склонностей, личностных качеств, уровня подготовки с требованиями профессиональной деятельности.

1) Сформировать умение строить жизненные планы с учётом конкретных социально-исторических, политических и экономических условий.

2) Создать условия для готовности учащихся к выбору профильного образования и будущей профессиональной деятельности, строить жизненные планы во временной перспективе.

1) Сформировать умение переводить дроби из десятичной в обыкновенную, и наоборот: из обыкновенной в десятичную; выявить условия возможности данных преобразований.

2) Тренировать умение читать и записывать десятичные дроби, применять свойства сложения, вычитания и умножения при выполнении заданий, работать с графиками зависимостей величин, решать задачи на дроби.

Задачи:

- образовательная: вырабатывать умение складывать и вычитать десятичные и обыкновенные дроби.

- развивающая: развивать навыки самостоятельной работы, самоконтроля, логическое мышление, математическую речь;

- воспитательная: воспитывать познавательный интерес, формировать устойчивые положительные мотивы.

Организация учебного процесса построена в рамках системно - деятельностного подхода ФГОС.

Заметки на полях.

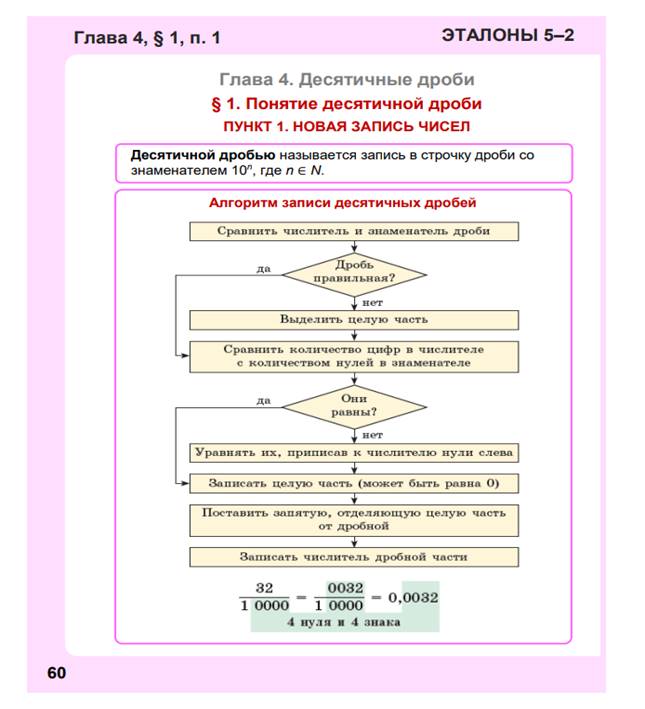
В пункте «Десятичные и обыкновенные дроби» рассматриваются условия преобразования дробей из десятичной дроби в обыкновенную дробь и обратно. Учащиеся должны понять, что от десятичной записи к записи в виде обыкновенной дроби можно перейти в любом случае, достаточно десятичную дробь записать с помощью дробной черты, и если это возможно, то сократить полученную обыкновенную дробь. Учащиеся могут сформулировать правило такого перехода и в другом виде: «Чтобы записать десятичную дробь в виде обыкновенной, можно выбросить из данной дроби запятую и полученное натуральное число поставить в числитель, а в знаменатель поставить единицу со столькими нулями, сколько знаков было после запятой».

В этом же пункте учащиеся сделают вывод, что обратный переход, от обыкновенной дроби к десятичной, возможен не всегда. В более подготовленном классе можно доказать ложность утверждения: «Всякую обыкновенную дробь можно записать в виде десятичной дроби».

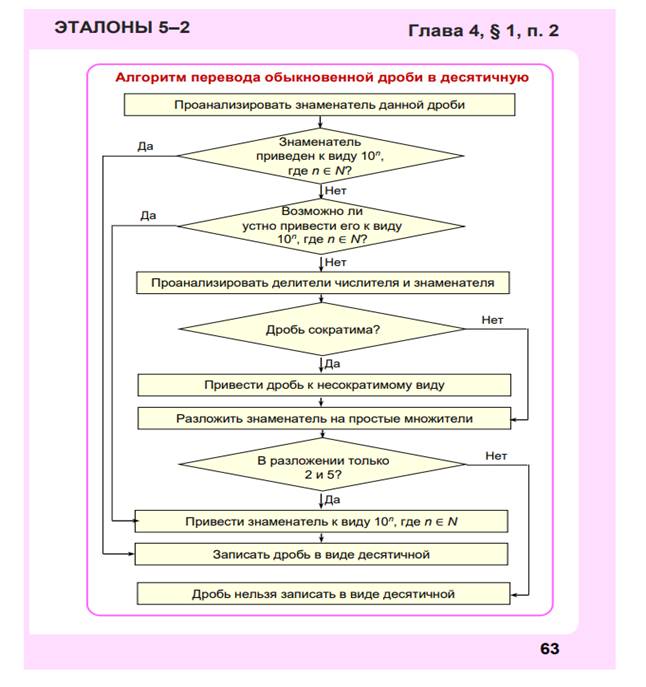
Учащиеся должны понять, что для того, чтобы определить возможность перевода обыкновенной дроби в десятичную, нужно использовать какой-то признак (условие) возможности такого перевода. Условие преобразования обыкновенной дроби в десятичную дробь учащиеся могут «открыть» сами.

На уроке тренируются умение выполнять следующие виды математических действий:

ü используют новую запись чисел;

ü преобразовывают десятичные дроби в обыкновенные и наоборот;

ü читают и записывают десятичные дроби;

ü приводят обыкновенные дроби к знаменателю 10ⁿ;

ü используют свойства арифметических действий для рационализации вычислений;

ü решают задачи на дроби;

ü работают с графиками.

Основные структурные элементы урока:

1. Новое знание: условие перевода десятичной дроби в обыкновенную дробь (вводится на актуализации знаний), условие перевода обыкновенной дроби в десятичную дробь.

2. Актуализация: запись десятичных дробей, сокращение дробей, разложением чисел на простые множители, приведение дробей к заданному знаменателю.

3. Пробное действие: назвать признак, помогающий среди данных дробей найти те, которые можно представить в виде десятичных дробей: .

Демонстрационный материал

Д-135.1 Алгоритм записи десятичной дроби.

Д-135.2 Эталон приписывания и отбрасывания нулей.

Д-135.3 Основное свойство дроби.

Д-135.4 Способы сокращения дробей.

Д-135.5 Условие перевода десятичной дроби в обыкновенную дробь.

Д-135.6 Условие перевода обыкновенной дроби в десятичную дробь.

Д-135.7 Алгоритм определения возможности перевода обыкновенной дроби в десятичную дробь.

Раздаточный материал

Р-135.1 Карточка для самопроверки заданий из домашней работы.

Р-135.2 Карточки с заданиями для урока.

Р-135.3 Блоки для алгоритма определения возможности перевода дроби в десятичную.

Р-135.4 Эталон для самопроверки самостоятельной работы.

Р-135.5 Карточка для этапа рефлексии.

Условные обозначения:

М5-2 Учебник «Математика, 5 класс», 2 часть (Г.В. Дорофеев, Л.Г. Петерсон).

Технологическая карта урока

№ п/п	Этап урока, цель, время	Содержание	Деятельность учителя	Деятельность учащихся	Форма		Материалы
№ п/п	Этап урока, цель, время	Содержание	Деятельность учителя	Деятельность учащихся	Социального взаимодействия	Работы	Материалы
1	*Мотивация к учебной деятельности.*	Приветствие, ознакомление с планом работы	Включение в деловой ритм. Устное общение. Можно провести следующий диалог: - Вспомните, чему вы научились на предыдущих уроках? – Почему вы только такие дроби рассматривали? – А как вы думаете, можно другие дроби представить в виде десятичных дробей? – Сегодня вы продолжите работу с дробными числами, и расширите знания о них. И выясните, любую ли дробь можно представить в виде обыкновенной дроби. Я уверена, что сегодня каждый из вас сможет сделать своё, пусть маленькое, но открытие. По какому плану вы будете работать?	*Подготовка класса к работе*. Участие в приветствии.	Групповая	Устная	Слайды 1-2. (Д-135.1-Д-135.4) На доске эталоны необходимые для открытия новых знаний.
2	*Актуализация знаний и фиксирование индивидуального затруднения в пробном учебном действии.*		*Направление деятельности учащихся.* *Слайды 3, 4* (Р-*135.1). Начать актуализацию целесообразно с самопроверки домашней работы. Слайды 5, 6* (Р-*135.2, Д-135.5). Практические задания с самопроверкой. Речевое клише:* - У кого нет ответа? - Что ты пока не смог сделать? - У кого есть ответ? - Каким эталоном ты воспользовался? - Зафиксируйте свое затруднение.	*Анализируют наглядный материал* Учащиеся определяют тему, цели урока. *Слайд 7.* Задание на пробное действие	в парах/группах. индивидуальная.	Устная	*Слайды 3-7.*
3	*Выявление места и причины затруднения.*		*Слайд 8.* Речевое клише: – Какое задание вы должны были выполнить? − Чем вы пользовались при выполнении задания? − Где у вас возникло затруднение? – Почему вы не смогли выполнить задание? (У нас нет эталона, по которому можно определить возможность перевода обыкновенной дроби в десятичную дробь.) * Если учащиеся после названных ими затруднений готовы сказать, почему они возникли, то анализ можно не проводить. Сразу продолжить диалог по выявлению причины затруднения.		фронтальная/в группах	Устная	*Слайд 8*
4	*Построение проекта выхода из затруднения.*		*Слайды 9.* Цель формулируется от причины затруднения. – Сформулируйте цель вашей деятельности. (Узнать правило, признак, по которому быстро можно определить возможность представления обыкновенной дроби в виде десятичной дроби.) − Чем вы сможете воспользоваться для достижения цели? Учащиеся предлагается средство для достижения цели (карточка с пропусками, блоки для построения алгоритма) и способы достижения цели (анализ, сравнение и обобщение) (Р-*135.2, Р-135.3*).	*Слайды 10, 11.* Учащиеся составляют в логическую последовательность шаги плана, представленного в (Р-*135.2*).	фронтальная/в группах	Устная, письменная	*Слайды 9,10, 11.*
5	*Реализация построенного проекта.*		*Слайд 12, 13.* Учащиеся работают по плану (при необходимости учитель может организовать подводящий диалог по плану). Учащиеся строят алгоритм условия перевода обыкновенной дроби в десятичную.	*Слайд 14.* (Д-*135.6, Д-135.7*) Согласовывается эталон. –Смогли преодолеть затруднение?	фронтальная/в группах	Устная, письменная	*Слайд 14*
5	*Реализация построенного проекта.*	*Физкультминутка*
6	*Первичное закрепление с проговариванием во внешней речи.*		*Слайд 15.* М5-2: № 729, стр. 158. М5-2: № 732 (1, 2), стр. 158.	*Слайд 16*. М5-2: № 732 (3, 4), стр. 158 с самопроверкой. На этом этапе рекомендуется обсудить с учащимися, у кого задания вызвали затруднения и в чем их причина.			*Слайд 16*.
7	*Самостоятельная работа с самопроверкой по эталону.*		Речевое клише - У кого возникли затруднения при выполнении задания? - В каком месте? - Почему у вас возникло затруднение? - Кто правильно выполнил задание?	*Слайд 17.* (Р-*135.4*) М5-2: № 730, стр. 158. Учащиеся учатся выполнять пошаговую самопроверку (если задание выполнено правильно, ставится знак «+», если допущены ошибки, то они исправляются).	индивидуальная	Устная, письменная	*Слайд 17.*
8	*Включение в систему знаний и повторение.*			*Слайды 18.* М5-2: № 731, стр. 158. *Слайды 19.* М5-2: № 735, стр. 158. *Слайды 20.* М5-2: № 736, стр. 159.	фронтальная/в парах	Устная, письменная	*Слайды 18-20.*
9	*Рефлексия учебной деятельности на уроке.*	Обоснование вывода урока, домашнее задание, оценки за урок.	*Слайд 21.* (Р-*135.5) Учащиеся заполняют карточку рефлексии индивидуально или проговаривают во внешней речи фронтально (в этом случае карточку рефлексии не раздаем). Речевое клише* – Что нового вы сегодня узнали? – Какие затруднения были при работе? - Какие цели вы ставили перед собой? – Что использовали при выходе из затруднения? – Проанализируйте свою работу на уроке. *Слайд 22.* Домашнее задание 1. Обязательная часть: п. 4.1.2.; № 739; № 740. 2. Дополнительные задания (по желанию): № 743*.	Осуществляют самооценку собственной учебной деятельности, соотносят цель и результаты, степень их соответствия.	фронтальная/в парах	Устная	Содержание урока

Скачано с www.znanio.ru

Государственное бюджетное общеобразовательное учреждение лицей №82

Технологическая карта урока

В этом же пункте учащиеся сделают вывод, что обратный переход, от обыкновенной дроби к десятичной, возможен не всегда

Пробное действие: назвать признак, помогающий среди данных дробей найти те, которые можно представить в виде десятичных дробей :

Технологическая карта урока № п/п

У кого нет ответа? - Что ты пока не смог сделать? -

Учащиеся предлагается средство для достижения цели (карточка с пропусками, блоки для построения алгоритма) и способы достижения цели (анализ, сравнение и обобщение) (

Самостоятельная работа с самопроверкой по эталону

Технологическая карта урока по математике в 5а классе ТЕМА: «ДЕСЯТИЧНЫЕ И ОБЫКНОВЕННЫЕ ДРОБИ» Иванова Зольфия Джавдетовна, учитель математики ГБОУ лицей №82 Петроградского района Санкт-Петербурга

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

29.01.2024