Тема 9. Поиск решений. Решение оптимизационных задач

КРАТКАЯ СПРАВКА

Табличный процессор MS Excel предоставляет пользователю еще один тип задач, получивших название оптимизационных.

Решение этих задач позволяет обосновать выбор такого варианта действий, который по тем или иным соображениям предпочтительнее других. Результат действий зависит от выбора некоторых параметров, определяющих условия ее осуществления. Выбор этих параметров называется решением. Для сравнения решений нужно иметь какой-то количественный показатель. А теории принятия решений он называется показателем эффективности, в математике – целевой функцией. В практике наиболее часто имеют место случаи, когда целевая функция должна получить максимальное или, наоборот, минимальное значение.

Решения, приводящие к получению результата, который по тем или иным показателям предпочтительнее других, называются оптимальными. Задача оптимизации может быть сформулирована следующим образом: при заданных условиях найти такое решение, которое позволяет получить экстремальное значение показателя эффективности. Для решения такой задачи используется инструмент Поиск решения.

Применяя Поиск решения важно знать какая это задача – линейная или нелинейная, так как алгоритмы оптимизации могут различаться и применение линейных алгоритмов к нелинейным задачам (или наоборот) может привести к ошибкам. При решении линейных задач необходимо установить флажок "Линейная модель" в окне "Параметры поиска решения".

Ещё одно важное для практики различие линейных и нелинейных задач: при решении линейных задач в качестве начальных приближений можно задать  любые произвольные числа – решение всё равно будет найдено. А для нелинейных задач начальные приближения должны быть достаточно близки к решению.

Примеры выполненных  заданий:

Пример №1:

Разработать план расходов на рекламу компании.

Общий бюджет фирмы, выделенный на рекламу, составляет 120000 рублей. В течение года печатаются объявления на страницах  6 изданий. Стоимость объявления в каждом издании разная и у каждого издания число читателей разное (данные предоставлены в таблице – рис.9.1.).

Оптимизировать затраты фирмы в пределах выделенной суммы и достичь максимального эффекта (максимальный эффект достигается при минимальных расходах на рекламу) при соблюдении следующих условий:

1.      необходимо чтобы число читателей было не менее 80000 человек;

2.      реклама была на страницах 6 изданий;

3.      в каждом издании должно быть напечатано не менее 6 объявлений

4.      нельзя тратить более ¼ всей суммы на одно издание

5.      общая стоимость размещения рекламы в издании 3 и в издании 4 не должна превышать 75000 рублей.

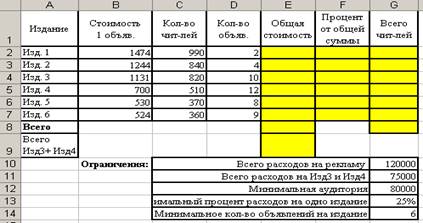
Рис.9.1. Образец таблицы с исходными данными

Решение:

Заполним данную таблицу следующим образом (рис.9.2.):

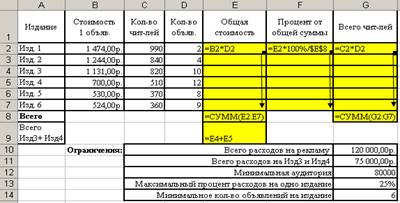
Рис.9.2. Образец заполнения таблицы

Установите в ячейках Е2:Е9 формат Денежный, в ячейках F2:F7 – формат процентный (пункт меню Формат/ячейки вкладка Число). После заполнения получим следующий вид таблицы (рис.9.3.):

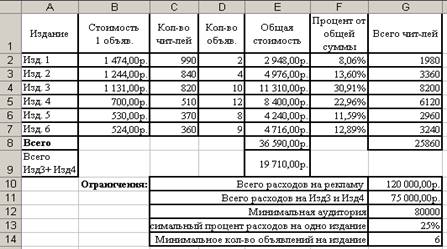
Рис.9.3. Результат заполнения таблицы

Теперь необходимо оптимизировать затраты фирмы в пределах выделенной суммы и достичь максимального эффекта. Максимальный эффект достигается при минимальных расходах на рекламу при соблюдении данных в задаче условий. Поэтому необходимо правильно заполнить окно Поиска решений и указать все условия (ограничения) в этом окне (рис.9.4.).

Вызвать окно можно с помощью команды Сервис/Поиск решения.

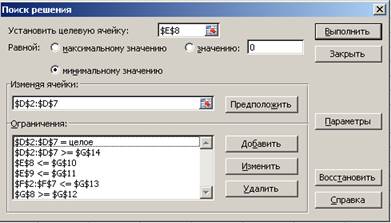
Рис.9.4. Образец заполнения окна Поиск решения

В результате нажатия кнопки  произойдет пересчет данных в таблице и будет подобрано  нужное количество объявлений, которое необходимо дать для достижения оптимального эффективного результата (рис.9.5.).

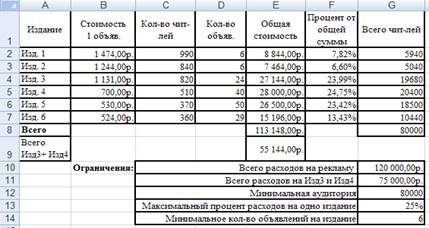
Рис.9.5.  Результат поиска решения

Пример №2

Предприятие выпускает три вида продукции А, В и С из одного и того же сырья 1,2 и3. Реализация единицы продукции А даёт прибыль 9 руб., В – 10 руб. а С – 16 руб. Сбыт продукции обеспечен, т.е. её можно производить в любых количествах, но запасы сырья ограничены.

В таблице (рис.9.6.) приведены нормы расхода сырья на производство единицы продукции и запасы трёх видов необходимого сырья:

Рис.9.6. Данные о нормах расхода и запасах сырья.

Найти план выпуска продукции, при котором прибыль будет максимальна, т.е. составить план выгодного производства продукции.

Решение:

Дополним таблицу с нормами расходов и запасов сырья (рис.9.6.) необходимыми данными. Таблица должна отражать и план выпуска, и расходы на изготовляемую продукцию (рис.9.7.).

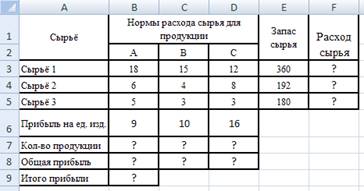
Рис.9.7. Образец расчетной таблицы

Выпуск продукции, т.е. количество продукции, необходимо найти. Но для начала их можно взять любыми или просто эти ячейки не заполнять – компьютер их сам подберет, а вот в другие ячейки необходимо обязательно ввести формулы для подсчета расхода сырья и прибыли.

Расчетные формулы имеют следующий вид:

Расход сырья = Норма расхода сырья * Кол-во продукции

Общая прибыль = Кол-во продукции * Прибыль на ед. изд.

Итого прибыли =  Общая прибыль А + Общая прибыль В + Общая прибыль С

Процесс заполнения таблицы изображен на рис.9.8.

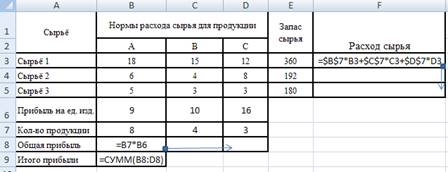
Рис.9.8. Образец заполнения таблицы

После заполнения таблицы мы получим таблицу, изображенную на рис.9.9.

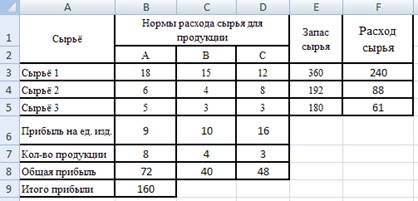
Рис.9.9 Заполненная таблица

А теперь вместо взятых нами параметров в ячейках В7:D7 необходимо подобрать такие, чтобы прибыль была максимальной и запасов сырья хватило на изготовление продукции. А также в ограничениях еще учесть, что количество продукции должно быть положительным и целым числом. Вызовем окно поиска решения (Сервис/Поиск решения) и заполним его (рис.9.10.)

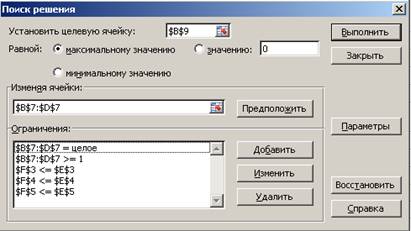
Рис.9.10. Задание параметров окна  Поиск решения

В результате нажатия кнопки  произойдет поиск решения и пересчет данных. В ячейках таблицы будет указано необходимое количество выпуска разного вида продукции для достижения максимальной прибыли (рис.9.11.).

Скачано с www.znanio.ru