Тема доклада: «Активизация познавательной деятельности учащихся в процессе обучения математики как важнейший фактор развития личности».

Тема доклада: «Активизация познавательной деятельности учащихся в процессе обучения математики как важнейший фактор развития личности».

“Обучение и воспитание должно развивать разум ребенка,

 должно зажечь в нем жажду серьезного труда, без которого жизнь его

 не может быть ни достойною, ни счастливою”.

 К.Д. Ушинский

Важной проблемой, определяющей сущность формирования личности, является деятельность, ее место в общественной жизни, ее влияние на развитие новых поколений. Проблема деятельности – это предмет изучения всех наук о человеческом обществе. Это – важнейшая основа развития человека, становление его как личности. “Деятельность – важнейшая форма проявления жизни человека, его активного отношения к окружающей действительности…»

У современных школьников отмечается равнодушие к знаниям, нежелание учиться, низкий уровень развития познавательных интересов. Поэтому я считаю, что главная задача педагога в этих условиях заключается в поиске более эффективных форм, моделей, способов и условий обучения. Таким образом, на первый план выходит проблема активизации деятельности учащихся в процессе обучения. Проблема активности личности в обучении – это ведущий фактор достижения целей обучения, общего развития личности, её профессиональной подготовки. Постоянно растущий объём информации, её многопрофильность привели к тому, что ни у кого не вызывает сомнения тезис о невозможности знать и уметь всё. Таким образом, наиболее ценным стало умение добиться цели через смежные знания, искать и находить решение. А одним из главных качеств личности ученика становится его готовность к самостоятельной деятельности по сбору, обработке, анализу и организации информации, умение принимать решения и доводить их до исполнения. Соответственно, меняются и задачи учителя. Теперь он должен быть не только и не столько источником информации, дающим знания, но и организатором самообразования учащихся, побуждающим к творческому поиску. Надо искать индивидуальные пути, что может быть осуществлено только в результате совместной творческой деятельности учителя и ученика. Стратегическим направлением активизации обучения является не увеличение объёма передаваемой информации, не усиление и увеличение числа контрольных мероприятий, а создание дидактических и психологических условий осмысленности учения, включения в него учащегося на уровне не только интеллектуальной, но личностной и социальной активности.

Математика объективно является одной из самых сложных школьных дисциплин и вызывает субъективные трудности у многих учащихся. В то же время имеются дети с явно выраженными способностями к этому предмету. Поэтому надо строить работу так, чтобы на уроках было интересно каждому учащемуся.

Обучение математике способствует умственному развитию, в процессе которого у учащихся вырабатываются умения обобщать и конкретизировать, систематизировать и классифицировать, проводить анализ. Формируются также личные качества: точность, сосредоточенность, внимание, настойчивость, ясность словесного выражения мысли. А как понять предмет, если он кажется ученику скучным, уроки однообразными? У определенной части учащихся наблюдается довольно низкий уровень интереса к учению, негативное отношение к знаниям. Из-за низкого уровня мыслительной деятельности учащиеся размышляют шаблонно, стремятся действовать знакомым способом. Проявление интереса к предмету можно добиться путём применения новых современных или как их сейчас называют инновационных технологий в обучении.

 Важное место в комплексе задач обучения математике занимает проблема активизации мыслительной деятельности обучаемых. Современная концепция обучения сегодня состоит в том, что учащийся должен учиться сам, а учитель – осуществлять мотивационное управление его учением, т.е. мотивировать, организовывать, координировать, консультировать его деятельность.

Нам знакомы следующие  принципы активизации познавательной деятельности:

1. Принцип проблемности

2. Принцип обеспечения максимально возможной адекватности учебно-познавательной деятельности характеру практических задач

3. Принцип взаимообучения

4. Принцип исследования изучаемых проблем

5.Принцип индивидуализации

6.Принцип самообучения

7 .Принцип мотивации

 Основная цель моей работы состоит в обеспечении условий для формирования совокупности знаний, умений, навыков учебно-познавательной деятельности учащихся на уроках математики. Для реализации этой цели я ставлю перед собой следующие задачи:

1. создание на уроках математики условий для активизации познавательной деятельности учащихся;

2. формирование и развитие общеучебных, самостоятельных, познавательных навыков учащихся;

3. создание условий для добывания знаний из реальной жизни, для овладения различными методами действий в нестандартных ситуациях;

4. способствовать выработке знаний и умений планирования, целенаправленности, анализа, самооценки познавательной деятельности у учащихся;

5. формирование у обучающихся способности владения различными методами познания.

 В основе моей работы лежит идея: формирования у учащихся деятельного состояния, которое характеризуется стремлением к учению, умственному напряжению и проявлениям волевых усилий в процессе овладения знаниями, что и является, по сути, развитием познавательной активности ребёнка.

 Способы активизации познавательной деятельности, которые я использую на уроках:

1. Создание атмосферы заинтересованности: достижение поставленной цели, оценка труда.

2. Стимулирование к диалогу, создание ситуации общения, то есть такой

 ситуации, в которой ребята должны:

Защищать свое мнение, приводить в его защиту аргументы, доказательства, использовать приобретенные знания;

Задавать вопросы учителю, товарищам, выяснять непонятное, углубляться с их помощью в процесс познания;

Рецензировать ответы товарищей, сочинения, другие творческие работы, вносить коррективы, давать советы;

Делиться своими знаниями с другими;

Помогать одноклассникам при затруднениях, объяснять им непонятное;

3. Побуждать учащихся находить не единственное решение, а несколько решений предпринятых самостоятельно

4. Смена форм деятельности повышает работоспособность ребят на уроке (устная работа, работа классом, самостоятельная работа, индивидуальные задания, самопроверка, игровые элементы)

5. Физкультурная минутка; можно пошутить, дать ребятам снять напряжение, усталость;

6. Попросить ребят составить карточки-задания друг для друга;

7. Сильный ученик опрашивает слабого (практикуется при доказательстве теорем);

8. Поощрение любой познавательной деятельности учащихся.

9. Высокий темп урока: план составляется так, чтобы каждый ребенок был занят, таким образом у учеников не остается свободного времени, чтобы отвлекаться (ни минуты свободного времени на уроке).

 Учебный труд, как и всякий другой, интересен тогда, когда он разнообразен. Однообразная информация и однообразные способы действия очень быстро вызывают скуку. Работа учителя по активизации познавательной деятельности учащихся наиболее эффективна, а качество знаний учащихся выше, если при проведении уроков используются приемы и средства, активизирующие их познавательный интерес. В своей работе я использую приемы, методы, которые позволяют вовлечь учащихся в активную, познавательную, творческую деятельность.

 В урок я включаю:

Занимательные задания

Занимательное содержание материала

Игровой материал

Составление кроссвордов

Заслушать написанные рефераты

Конкурсы, соревнования

 Различные формы проведения урока позволяют разнообразить учебный процесс. Дети охотно включаются в работу, ведь здесь нужно проявить знания, смекалку, творчество. Дети с удовольствием решают задачи, играя, соревнуясь.

Устный счет.

 Большое значение в обучении имеет организационный момент урока. Чтобы быстро настроить детей на работу, но сделать это без понуканий и строгости я начинаю урок с устного счета. В своей работе я применяю два вида устного счета. Первый – это тот, при котором числа демонстрируются перед учащимися с использованием карточек, ПК, записи на доске и при этом читаются. Работает зрительное, слуховое восприятие учащихся, чем существенно облегчается процесс вычисления. Второй вид устного счета – это когда учащиеся воспринимают числа и действия над ними на слух. Второй вид устного счета сложнее первого, но эффективнее в методическом смысле. Однако однообразие заданий в виде примеров на вычисление уменьшает интерес как к счету, так и к уроку вообще, поэтому в своей работе я использую различные приемы устного счета, например, игровые.

 Примеры могут быть оформлены в виде индивидуального лото («Действия с натуральными числами», «Действия с десятичными дробями», «Признаки равенства треугольников» и другие). Всевозможные формы кодированных ответов, ребусов привлекают внимание ребят. Для упражнения в вычислениях можно предложить ребятам поиграть  в такие игры как, «Собери цветы», «Собери грибы», «Поймай рыбку» и т. д. на обратной стороне цветов, грибов, рыбок   написаны примеры, которые им предстоит решить (такие игры я провожу не только на этапе устного счета, но и на уроках закрепления материала). Для устного счета я также использую такие игры : «Лесенка», «Молчанка», «Удивительная цепочка» (решение уравнений: в каждое уравнение, начиная со второго, вставляется корень предыдущего уравнения).

Тема «Решение квадратных уравнений»: «Лесенка» или «Пирамида»

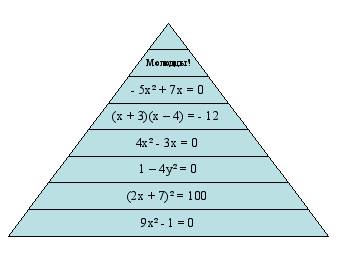
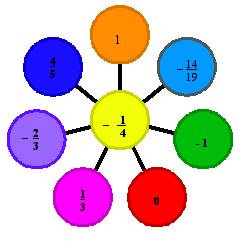
Интересны для учащихся устные коллективные разминки, занимающие не более 5 минут, развивающие быстроту реакции, внимательность, умение четко и конкретно мыслить. В такие разминки следует включать вопросы, требующие однозначного, быстрого хорового ответа и направленные на актуализацию опорных знаний, и на проверку домашнего задания, и на отработку каких либо математических понятий и определений.

Например (6 класс):

1. Число не являющееся ни положительным, ни отрицательным.

2. Самое маленькое целое положительное число.

3. Самое большое целое отрицательное число.

4. Дробь, равная 50%.

5. Числа, имеющие не более двух делителей.

6. Одна сотая часть числа.

7. Назовите дробь 3/4 в процентах.

8. Наименьшее положительное двузначное число.

9. Число, не являющееся делителем ни одного из чисел.

10. Треть от трети.

11. Половина четверти.

12. Сумма противоположных чисел.

13. Набольшее отрицательное двузначное число….

Неоценима на уроках математики роль физминуток, которые можно проводить не только для двигательной активности учащихся, но и для отработки математических правил в игровой форме.

Например:

1. У меня набор карточек с правильными и неправильными дробями. Если показываю правильную дробь - руки вверх, неправильную - руки в стороны.

2. У меня набор карточек с примерами на сложение чисел с разными знаками. Если сумма отрицательна - присели, положительна - встали.

3. На доске записаны примеры, а я говорю ответ, если ответ верный - учащиеся хлопают в ладоши, а неправильный - топают ногами.

Игра

 В своей работе большое внимание уделяю игре. Игра – творчество, игра – труд. В процессе игры у детей вырабатывается привычка сосредоточиваться, мыслить самостоятельно, развивается внимание, стремление к знаниям. Увлекшись, дети не понимают, что учатся: познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию. Даже самые пассивные из детей включаются в игру с огромным желанием. Во время игры дети, как правило, очень внимательны, сосредоточены.

 Включение игры в учебный процесс повышает интерес к предмету, т.к. в процессе игры мышление протекает более активно под воздействием положительных эмоций, соревнования, желания выиграть. Игра - метод обучения, и с её помощью должны решаться образовательные, развивающие и воспитательные задачи.

В процессе проведения игры я стараюсь реализовать следующие цели:

1 .Образовательная - закрепление и обобщение полученных знаний,  включение элементов занимательности интереса в урочную и неурочную работу для более успешного усвоения материала, получения новых знаний в процессе игры;

2. Развивающая - умение сопоставить и сравнить факты, делать самостоятельные выводы; развивать творческую самостоятельность учащихся, творческое мышление, умение работать с различными источниками информации.

3. Воспитательная - формирование интереса к предмету; воспитание чувства коллективизма, ответственности за результаты своей работы и учёбы.

В своей работе я использую следующие виды игр:

настольные;

игры- состязания;

интеллектуальные.

 Чаще всего в форме игры я провожу повторительно-обобщающие уроки: это соревнования, игра-путешествие; игровые моменты стараюсь включить в каждый урок. Кроме активизации работы учащихся, соревнования несут и воспитательную нагрузку: ребята сопереживают успехам товарищей. Нестандартный урок - переход в иное психологическое состояние, это другой стиль общения, положительные эмоции, это возможность каждому проявить себя в новом качестве, это возможность каждому развить свои творческие способности. Дети, как правило, бывают поставлены в ситуацию успеха, что способствует пробуждению их активности в работе на уроке.

Например, игра «Кодирование ответов», индивидуальное лото и т.д.

Сообщение сведений из истории математики.

 Там, где это оправдано программой, вводной частью урока, возбуждающей интерес и внимание учащихся, может и должен быть короткий увлекательный рассказ, связанный с историей математики. Такие краткие экскурсы в прошлое математики вызывают у учащихся интерес. Сообщение сведений из истории науки полезно и в познавательном плане, ибо способствует формированию у учащихся мировоззрения. Такое изложение даст возможность показывать учащимся при изучении каждого нового раздела или темы, что математика как наука о пространственных формах и количественных отношениях реального мира возникла и развивается в связи с практической деятельностью человека.

Исторический материал я использую на разных этапах урока. Иногда эти сведения даю перед объяснением нового материала, иногда связываю его с отдельными вопросами темы урока, а иногда даю как обобщение или итог изучения какого-нибудь раздела, темы курса математики. В первом случае исторические сведения помогут лучше мотивировать важность новой темы и нового раздела, что вызовет интерес учащихся к их изучению.

Таким образом, учащиеся постепенно приучаются к самостоятельной работе со справочной и учебной литературой.

Для кратких исторических сведений иногда достаточно 2— 5 мин урока. Затрата времени окупается повышением интереса к данной теме.

Самостоятельная работа

 Самостоятельное выполнение заданий – самый надёжный показатель качества знаний, умений и навыков учащихся. Ученик, получая теоретически обоснованные способы действий, знания, может самостоятельно вырабатывать подобные способы при решении поставленных проблем.

Рассматривая структуру самостоятельной познавательной деятельности учащихся, я пришла к выводу о необходимости повышения количества разнообразных самостоятельных работ в учебном процессе. В своей работе для проверки знаний использую тест. Он позволяет провести более широкий тематический контроль материала на ту или иную тему, а может быть, и на ряд тем. Тест позволяет сэкономить время на уроке. Интенсивная работа при тестировании в 5-9 классах повышает заинтересованность учащихся в хорошем результате. Кроме того, тест благотворно влияет на развитие интуиции и логического мышления.

Путь к этому лежит через разнообразную самостоятельную работу учащихся, организованную в соответствии с особенностью интереса, занимательность, а также через творческие работы учащихся.

В своей работе я использую разные виды тестов.

 Тесты, в которых предполагают верное заполнение пропусков в утверждениях, формулировках определений, теорем, свойств здесь же, в тексте.

Так, например, тест в 7 классе по теме «Начальные сведения по геометрии».

Слово «геометрия» в переводе с греческого означает ____________.

Через любые _______ точки можно провести прямую и притом только одну.

Часть прямой, ограниченная двумя точками, называется __________.

Точка отрезка, делящая его пополам, называется __________отрезка.

Геометрическую фигуру, которая состоит из точки и двух лучей, исходящих из этой точки, называют _______________.

Градус – угол, равный __________ части развернутого угла.

Угол называется ___________, если он равен 90º.

Для измерения углов используют ______________.

Тесты, в которых надо определить истинны или ложны следующие утверждения.

Тесты, в которых предлагается из предложенных ответов выбрать верный, отметить его в тексте кружочком или квадратиком.

 Использую тест и для проведения промежуточной аттестации.

Пожалуй, главной функцией самостоятельной работы является формирование высококультурной личности, т.к. только в самостоятельной интеллектуальной и духовной деятельности развивается человек.

 Для активизации учебной деятельности школьников, воспитания у них  самостоятельности мышления, умения применять знания в процессе обучения я использую фронтально-индивидуальную и обучающую самостоятельные работы.   

Фронтально-индивидуальная.

 Образец решения задания записывается на доске и разбирается его пошаговое выполнение. После чего учащимся предлагается выполнить задание по образцу, при этом затрудняющимся оказывается помощь. Такая работа носит воспроизводящий характер, но она незаменима при формировании новых умений и навыков, при отработке алгоритмических действий. Обучающая.

 В решении задания пропущены объяснения или (и) вычисления. Учащийся должен восстановить решения задания полностью. При выполнении такой работы формируется объем активных знаний учащихся, умение обосновывать решение, применять изученные теоретические положения на практике.

ИКТ

Чтобы сохранить интерес к предмету и сделать качественным учебно-воспитательный процесс нами на уроках активно используются информационные технологии.

Применение компьютерных программных средств на уроках математики позволяет учителю не только разнообразить традиционные формы обучения, но и решать самые разные задачи: заметно повысить наглядность обучения, обеспечить его дифференциацию, облегчить контроль знаний учащихся, повысить интерес к предмету, познавательную активность школьников. В своей работе я использую презентации, которые содержат демонстрационные программы для объяснения нового материала,

для закрепления изученного, программы для организации устного счета. Использование таких презентаций дает хороший результат. Мною используются также диски по математике.

 Применение электронных обучающих средств на уроках обеспечивает:

-      экономию времени при объяснении нового материала;

-      представление материала в более наглядном, доступном для восприятия виде;

-      воздействие на разные системы восприятия учащихся, обеспечивая тем самым лучшее усвоение материала;

-      постоянный оперативный контроль усвоения материала учащимися.

Это, в целом, стимулирует разнообразие творческой деятельности учащихся, дает возможность увеличения объема информации, воспитывает навыки самоконтроля, повышает интерес к предмету.

 Одним из главных качеств личности ученика становится его готовность к самостоятельной деятельности по сбору, обработке, анализу и организации информации, умение принимать решения и доводить их до исполнения.

Я попыталась выделить несколько групп обобщения материала для проведения мотивационного этапа. Систематизировать данный материал достаточно сложно, потому что иногда материал очень тесно перекликается и поэтому его трудно отнести к конкретной группе.

Например, по темам:

1. Линейные уравнения.

Эпизод из жизни М.Ю.Лермонтова:

– Задумайте какое угодно число, и я с помощью простых арифметических действий определю его, – предложил М.Ю.Лермонтов.

– Хорошо, я задумал, – сказал один из стоявших вокруг него офицеров…

– Благоволите прибавить к нему еще 25. Теперь не угодно ли прибавить еще 125? Засим вычтите 37. Еще вычтите число, которое вы задумали сначала. Теперь остаток умножьте на 5. Засим полученное число разделите на 2. Теперь посмотрим, что у вас должно получиться. Если не ошибаюсь, число 282?.

Офицер даже привскочил, так поразила его точность вычисления:

– Да, совершенно верно.

На чем основан фокус?

2. Сумма углов треугольника.

Задача: Как измерить изображенный на доске угол, часть которого вместе с вершиной случайно стерли? (Обыграть, что учитель растерян, ему требуется помощь)

Например, по теме “Теорема Пифагора” можно использовать следующий материал:

3.Практическая работа.

Задание по рядам: построить прямоугольные треугольники с катетами 3 и 4; 12 и 5 ; 6 и 8; 8 и 15 и заполнить таблицу

Формируя мотивацию обучения, я использую различные приёмы.

Например «урок без темы»

В начале урока тема не объявляется. После того как ребята получили стимул, тема изучается, формируются первые навыки. После этого нужно обязательно вернуться к заданию, с которого начиналось изучение темы, и дать возможность ребятам решить задание повторно.

Условия для мотивации достижения создаю также через проблемную ситуацию.

Тема. “Арифметическая прогрессия”

Я предлагаю решить задачу из биографии К.Ф. Гаусса. Однажды учитель, чтобы занять первоклассников, пока он будет заниматься с учениками третьего класса, велел сложить все числа от 1 до 100, надеясь что это, займет много времени. Но маленький Гаусс сразу сообразил, что 1+100=101, 2+99=101 и т. д. И таких чисел будет 50. И умножив 50 на 101, получил результат в уме, едва учитель закончил чтение условия.

Такой же небольшой эксперимент провожу на уроке со своими учениками. Даю некоторое время для вычисления. Заслушиваем результаты ребят и способ вычисления. Если рационального способа нет, то объявляется тема.

Примером можно взять и биологическую статистику, т. е. “ В благоприятных условиях бактерии размножаются так, что за одну минуту одна из них делится на две. Сколько их будет через час?”

Таким образом, хорошо известно, что ничто так не привлекает внимания и не стимулирует работу ума, как удивительное и оно не просто привлекает внимание «здесь и сейчас», но и удерживает интерес в течении длительного отрезка времени.

Тригонометрия в ладони. Оказывается, значение синусов и косинусов углов «находятся» на нашей ладони.

Литература

Формирование познавательных интересов школьников.// Под ред. Щукиной Г.И. Л., 1968.

Коваленко В.Г. Дидактические игры на уроках математики: Кн. Для учителя. – М.: Просвещение, 1990.

Истомина Н.Б. Активизация учащихся на уроках математики. Пособие для учителя. – М.: Просвещение. 1985.

Окунев А.А. О развитии творческих способностей учащихся: Кн. Для учителя: Из опыта работы. – М.: Просвещение, 1988.

Касьяненко М.Д. Активизация познавательной деятельности учащихся при изучении математики. – М. Просвещение, 1988.

Математика 5 – 11 классы: нетрадиционные формы организации тематического контроля на уроках / авт.-сост. М.Е. Козина, О.М.Фадеева. – Волгоград: Учитель,2006

Ситникова Т.В. Приемы активизации учащихся в 5 – 6 классах.// Математика в школе. 1993, №2 с. 24

Ахметгалиев А. Мотивация деятельности на уроках математики.// .// Математика в школе. 1996, №2 с. 56-60

Широкова Л.А. учебная программа в форме игры. // Математика в школе. 1994, №2 с.50

Егорова Л.И. Создание ситуации успеха на уроке.// Математика в школе. 1996, №6 с.3 – 5.