Тема урока: Геометрический смысл определенного интеграла (вычисление площадей плоских фигур)

Тема урока: Геометрический смысл определенного интеграла              (вычисление площадей плоских фигур)    Урок №  Цели урока: 1. Обучающая: Рассмотреть геометрический смысл определенного интеграла и его применение для вычисления площадей плоских фигур.  Развивающая: Способствовать развитию логического мышления, памяти. 2.         3. Воспитательная: Аккуратное ведение конспектов, самодисциплина.    : Урок изучения нового материала          Тип  урока        Вид урока: комбинированный         Методы:  словесные                 Оборудование: мультимедийный проектор, экран. Ход урока.  I. Оргмомент II. Актуализация опорных знаний        Анализ сам.работы из практического занятия № 8  II. Целевая установка. 1. Тема урока                      2. Цель урока III. Формирование новых понятий и способов действий.      Площадь фигуры, ограниченной осью 0x, двумя вертикальными прямыми x = a, x = b и  графиком функции f (x) (рис.1), определяется по формуле                          Рис.1     Пусть F (x) и G (x) ­ первообразные функций f (x) и g (x), соответственно. Если f (x) ≥ g (x) на  замкнутом интервале [a, b], то площадь области, ограниченной двумя кривыми y = f (x), y = g (x) и вертикальными линиями x = a, x = b (рис.2), определяется формулой                        Рис.2                           Рис.3                             Рис.4          Если   же   область   расположена   под   осью   Ох   (Рис.3),   то   площадь   области   в   этом   случае определяется по формуле:   И, наконец, случай, изображённый на рис. 4. В этом случае площадь фигуры вычисляется по формуле:IV.  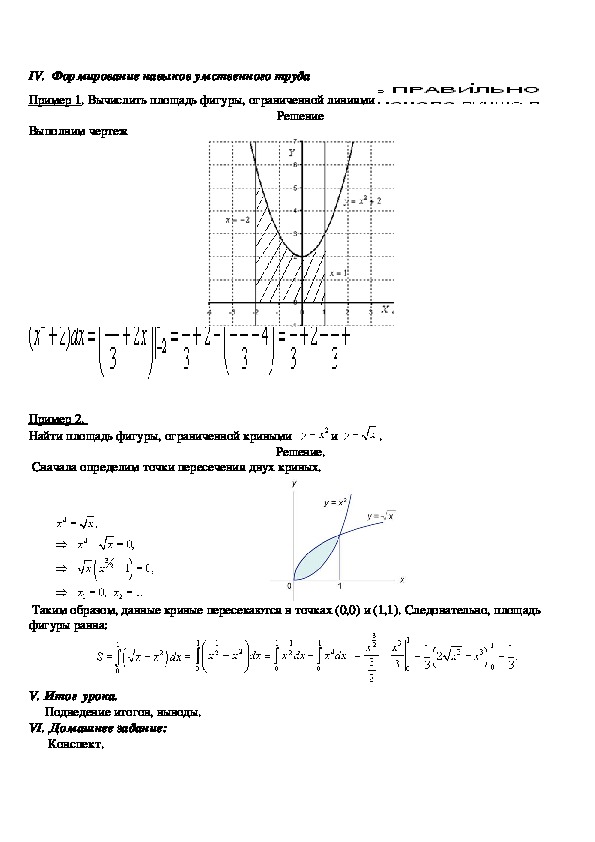Формирование навыков умственного труда Пример 1. Вычислить площадь фигуры, ограниченной линиями  Решение Выполним чертеж Пример 2.  Найти площадь фигуры, ограниченной кривыми   Решение.  Сначала определим точки пересечения двух кривых.  и  .            Таким образом, данные кривые пересекаются в точках (0,0) и (1,1). Следовательно, площадь  фигуры равна:                                      V. Итог  урока.       Подведение итогов, выводы. VI. Домашнее задание:           Конспект.