Теорема Фалеса. Пропорциональные дидактичесий материал

Фале́с (др.-греч. Θαλῆς ὁ Μιλήσιος, 640/624 — 548/545 до н. э.) — древнегреческий философ и математик из Милета (Малая Азия). Представитель ионической натурфилософии и основатель милетской (ионийской) школы, с которой начинается история европейской науки. Традиционно считается основоположником греческой философии (и науки) — он неизменно открывал список «семи мудрецов», заложивших основы греческой культуры и государственности.

Теорема Фалеса. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Значит, если   и выполняется равенство  то так же выполняется равенство .

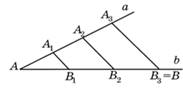
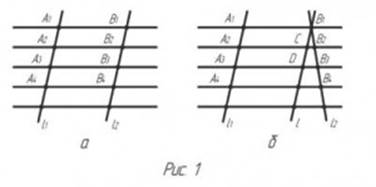
Доказательство теоремы: Пусть отложены одинаковые отрезки А₁А₂, А₂А₃, А₃А₄, ... на прямой l₁ и проведены параллельные прямые через их концы, которые пересекают в точках В₁, В₂, В₃, В₄, ... прямую l₂ (рис.1). Необходимо доказать, равны друг другу отрезки В₁В₂, В₂В₃, В₃В₄, ...

Докажем, к примеру, что В₁В₂ равен В₂В₃.

Рассмотрим, прежде всего, условие, когда параллельны друг другу прямые l₁ и l₂ (рис. 1а). В этом случае, мы имеем А₁А₂ = В₁В₂, а также А₂А₃ = В₂В₃, как стороны параллелограммов, противоположно расположенные относительно друг друга, то есть А₁В₁В₂А₂ и А₂В₂В₃А₃, поскольку А₁А₂=А₂А₃, тогда и В₁В₂=В₂В₃.

При условии, что не параллельны прямые l₁ и l₂, то проведем через точку В₁ прямую l, которая будет параллельна прямой l₁ (рис.1б). В этом случае, она пересечет в некоторых точках С и D прямые А₂В₂ и А₃В₃. Тогда, так как А₁А₂=А₂А₃, имеем по доказанному В₁С=СD. И получаем отсюда В₁В₂=В₂В₃. Точно также можно доказать и то, что В₂В₃=В₃В₄ и т.п.

Список литературы:

1. https://ru.wikipedia.org/wiki/%D0%A4%D0%B0%D0%BB%D0%B5%D1%81_%D0%9C%D0%B8%D0%BB%D0%B5%D1%82%D1%81%D0%BA%D0%B8%D0%B9  
2. Геометрия 8 Шыныбеков А.Н. Учебник для 8 класса общеобразовательной школы. 2-е изд. – Алматы: Атамұра, 2011 – 128 с. ISBN 978-601-282-320-2

3. Скачано с www.znanio.ru