Требования к уроку по ФГОС

Частное общеобразовательное учреждение

«Средняя школа им. Н.И.Лобачевского»

Исследовательская работа по математике

Практическое применение графов

                                                                Автор работы:

Цыбульский Артем Николаевич

                            ученик 8 класса

Наставник:

Лукьянова Екатерина Владимировна,

                           1 категория, учитель математики

ЧОУ «СШ им. Н.И.Лобачевского» 

Дзержинск

2021 год

СОДЕРЖНИЕ

Введение

В математике и смежных с ней дисциплинах существует класс задач, которые наиболее просто и понятно решаются с применением теории графов. Это замечательные математические объекты, применяя которые можно решать логические задачи. Также c применением графов можно решать различные головоломки и упрощать условия задач. Я решил узнать, как можно применить теорию графов на практике, в жизни, т.к. в обязательном курсе школьной программы такой раздел отсутствует. Возникшая проблема стала главной причиной выбора темы данной исследовательской работы.

Теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Графы буквально вездесущи. В виде графов можно, например, интерпретировать схемы дорог и электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей. За последние четыре десятилетия теория графов превратилась в один из наиболее бурно-  развивающихся разделов математики. Это вызвано запросами стремительно расширяющейся области приложений.

Тема моей работы:

Актуальность выбранной темы обусловлена частым использованием графов во многих сферах жизни.

Цель исследовательской работы:

овладеть основными понятиями   теории графов и новыми для школы методами решения задач.

В этой работе поставлены следующие задачи:

•        Изучить основные понятия теории графов и виды графов.

•        Разобрать решения задач с помощью графов.

•        Узнать о применении графов в науке и в различных сферах.

          Гипотеза графы имеют большое значение в геометрии, и применяются в широком круге областей.

Объектом исследования в данной работе являются графы и задачи на их построение.

Предмет исследования: применение графов в разных видах деятельности.

Методы исследования: анализ, умозаключение.

Практическая ценность: данный материал может использоваться как методическое пособие на факультативных занятиях по математике.

I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. История графов и их значение

Родоначальником теории графов считается Леонард Эйлер. В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов. Термин «граф» впервые ввел Сильвестр, Джеймс Джозеф в 1878 году в своей статье в Nature.

Возникший в XIII веке город Кёнигсберг (ныне Калининград) состоял из трёх формально независимых городских поселений и ещё нескольких «слобод» и «посёлков». Расположены они были на островах и берегах реки Прегель, делящей город на четыре главные части: А) Альтштадт, Б) Кнайпхоф, В) Ломзе, Г) Форштанд. Для связи между городскими частями уже в XIV веке стали строить мосты. В связи с постоянной военной опасностью мосты имели оборонные качества. Мосты были местом шествий, религиозных и праздничных процессий, по мостам проходили православные крестные ходы.

2. Понятие графа

         Графом в математике называется конечное множество точек, некоторые из которых соединены линиями. Точки называются вершинами, а соединяющие линии - ребрами графа.

         При взгляде на географическую карту сразу бросается в глаза сеть железных дорог. Это типичный граф: кружочки обозначают станции - вершины графа, а соединяющие их пути - ребра.

         Инженер чертит схемы электрических цепей. Химик рисует структурные формулы, чтобы показать,  как в сложной  молекуле с помощью валентных связей соединяются друг с другом атомы. Историк прослеживает родословные связи по генеалогическому дереву. Военачальник наносит на карту сеть коммуникаций, по которым из тыла к передовым частям доставляется подкрепление. Социолог на сложнейшей диаграмме показывает, как подчиняются друг другу различные отделы одной огромной корпорации.

         Что общего во всех этих примерах? В каждом из них фигурирует схема, состоящая из точек (они обозначают разветвления  электрической цепи, атомы, людей, города и т.д.), соединённых между собой линиями.

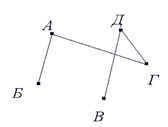
Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?

Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями. 

Теперь нам видно, что долететь с Земли до Марса на рейсовых ракетах нельзя.

Задача 2. В одном городе шесть станций метро: Алмазная, Золотая, Лесная, Парковая, Садовая, Серебряная. Поезда следуют по маршрутам Алмазная – Золотая, Золотая – Серебряная, Серебряная – Алмазная. Лесная – Садовая, Садовая – Парковая, Парковая – Лесная. Можно ли с помощью этих поездов добраться со станции Парковая до станции Алмазная?

Решение: Нарисуем картинку, на которой будем отмечать станции точками, а соединяющие их маршруты – непересекающимися линиями.

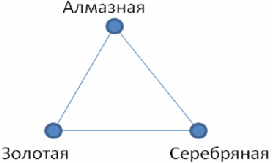
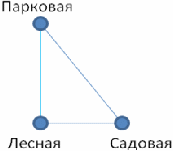
 Ответ: добраться со станции Парковая до станции Алмазная нельзя.

         Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – графическое представление решения. При этом и картинки, нарисованные для каждой задачи, оказались похожими: каждая картинка – это несколько точек, некоторые из которых соединены линиями. Такие картинки и называются графами. Точки при этом называются вершинами, а линии – ребрами графа. Заметим, что не каждая картинка такого вида будет называться графом. Например,  если нарисовать в тетради пятиугольник, то такой рисунок графом не будет.

         Граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:

Такие одинаковые, но по-разному нарисованные графы, называются изоморфными

       Что общего у схем, которые помогли  решить нам задачи? Все они состоят из точек (кружков) и  отрезков, соединяющих пары точек. Рассмотрение таких схем и приводит к понятию графа.

      Граф представляет собой непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.

Обозначать граф будем буквой Г.  При изображении графов на рисунках или схемах отрезки могут быть прямолинейными и криволинейными; длины отрезков и расположение точек произвольны.

       Все три фигуры на рисунке  изображает один и тот же граф.

3. Виды графов

1.     Ориентированный граф (кратко орграф) — рёбрам которого присвоено направление.

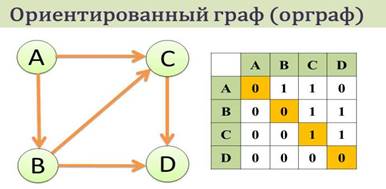
2.     Неориентированный граф - это граф, в котором нет направления линий.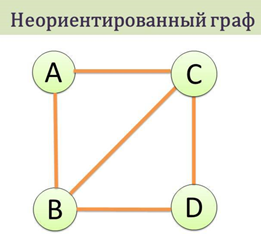

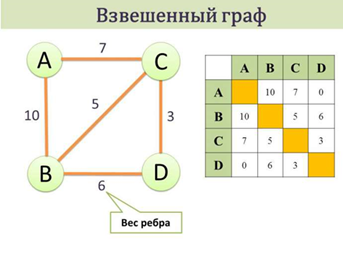
3.Взвешенный граф – дуги или ребра имеют вес.

4. Связный граф

Две  вершины А и В графа называются связными, если в графе существует путь с концами А и В.

        Две вершины графа называются  несвязными, если в графе не существует ни одного пути, связывающего их.

         Про граф, изображенный на рисунке, говорят, что он связный, так как из каждой вершины по ребрам можно попасть в любую другую.

         Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф.

4. Полнота графа

  Схема графа, состоящая из «изолированных» вершин, называется нулевым графом.

Графы, в которых не построены все возможные ребра, называются неполными графами.

Графы, в которых построены все возможные ребра, называются полными графами.

5. Степень вершины

Степенью вершины называется число ребер  графа, которым принадлежит эта вершина.     

      У графа на рисунке  (а): степень= 1; на рисунке (б) степень = 2. У графа на рисунке  (в) степени всех вершин равны нулю.

      Вершина называется нечетной, если ее степень – число нечетное. Вершина называется четной, если ее степень – число четное.  

Если степени всех вершин графа равны, то граф называется однородным. Таким образом, любой полный граф — однородный

      Имея даже общие представления о графе, иногда можно судить о степенях его вершин. Так, степень  каждой вершины полного графа на единицу меньше числа  его вершин. При этом некоторые закономерности, связанные со степенями вершин, присущи не только полным графам.

6. Свойства графов.

1. Если все вершины графа четные, то можно одним росчерком (т.е. не отрывая карандаша от бумаги и не проводя дважды по одной и той же линии) начертить граф. При этом движение можно начать с любой вершины и окончить в той же вершине.

Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым. Такими графы названы в честь учёного Леонарда Эйлера.

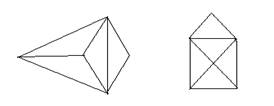
2. Граф с двумя нечетными вершинами тоже можно начертить одним росчерком. Движение нужно начинать от любой нечетной вершины, а заканчивать на другой нечетной вершине.

3. Граф с более чем двумя нечетными вершинами невозможно начертить одним росчерком.

4. Число нечетных вершин графа всегда четное.

Доказательство: Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.

5. Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф будет равно половине числа нечетных вершин этого графа.

II. ИССЛЕДОВАТЕЛЬСКАЯ ЧАСТЬ

1. Применение графов к решению задач по математике.

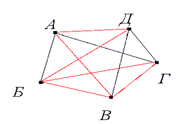
Задача 1.

Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано?

Решение:

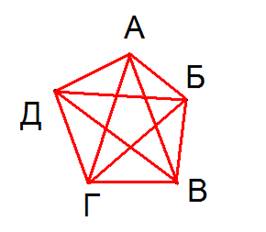Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена.

  Если подсчитать число ребер графа, изображенного на рисунке справа, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.

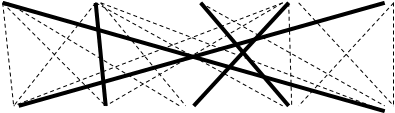
Задача 2.  В небольшом городке живут пять друзей: Иванов, Петренко, Сидорчук, Гришин и Капустин. Профессии у них разные: один из них маляр, другой- мельник, третий- плотник, четвертый-почтальон, а пятый- парикмахер.

Петренко и Гришин никогда не держали в руках малярной кисти.

Иванов и Гришин собираются посетить мельницу, на которой работает их товарищ. Петренко и Капустин живут в одном доме с почтальоном.

Сидорчук был недавно в ЗАГСе одним из свидетелей, когда Петренко и дочь парикмахера сочетались законным браком. Иванов и Петренко каждое воскресенье играют в городки с плотником и маляром.

Гришин и Капустин по субботам обязательно встречаются  в парикмахерской, где работает их   друг. Почтальон предпочитает бриться сам. Кто есть кто?

Решение.

  Иванов       Петренко  Сидорчук    Гришин        Капустин

  маляр          мельник   плотник     почтальон      парикмахер

Задача 3. В одном дворе живут четыре друга. Вадим и шофер старше Сергея, Николай и слесарь занимаются боксом, электрик-младший из друзей.

По вечерам Андрей и токарь играют в домино против Сергея и электрика.

Определите профессию каждого из друзей.

Решение.

Составим граф из 4 друзей и 4 профессий. Пунктирными линиями отметим невозможные связи, а сплошной - соответствие имени и профессии.  Если от каждой вершины выходить 3 пунктирных линии, то четвертая линия должна быть  сплошной.

        В                          С                      Н                         А

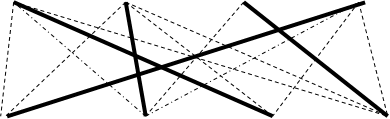        Ш                          С                         Т                        Э

Задача 4. При составлении расписания на понедельник в IX классе преподаватели высказали просьбу завучу.

Учитель математики: «Желаю иметь первый или второй урок».

Учитель истории: «Желаю иметь первый или третий урок».

Учитель литературы: «Желаю иметь второй или третий урок».

Какое расписание будет составлено, если по каждому предмету может быть только один урок?

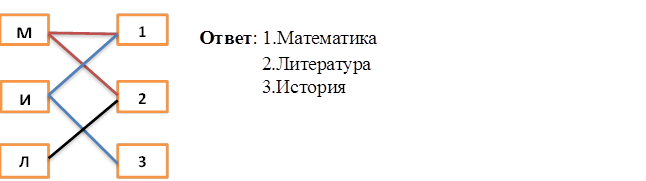
Задача 5. На соревнованиях по легкой атлетике Андрей, Боря, Сережа и Володя заняли первые четыре места. Мнения девочек разошлись, как места распределились между победителями.

Даша. Андрей был первым, Володя – вторым

Галя. Андрей был вторым, Борис – третьим

Лена. Боря был четвертым, Сережа – вторым.

Ася, которая была судьей на этих соревнованиях, сказала, что каждая из девочек сделала одно правильное и одно неправильное заявление. Кто из мальчиков какое место занял?

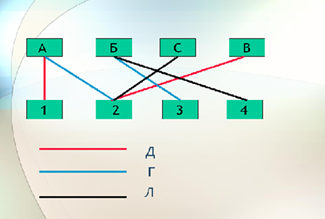
Ответ: Андрей – 1 место, Сергей – 2 место, Борис-3 место, Володя -4 место.

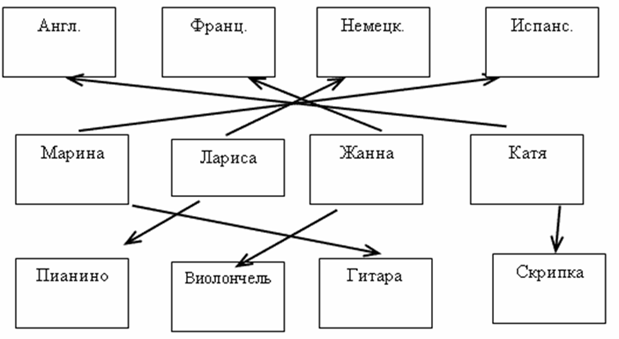
Задача 6. Марина, Лариса, Жанна и Катя умеют играть на разных инструментах    (пианино, виолончели, гитаре, скрипке), но каждая только на одном. Они же знают иностранные языки (английский, французский, немецкий и испанский), но каждая только один. Известно:

1.Девушка, которая играет на гитаре говорит на испанском.

2.Лариса не играет ни на скрипке, ни на виолончели и не знает английского языка.

3.Марина не играет ни на скрипке, ни на виолончели и не знает ни немецкого, ни английского.

4.Девушка, которая говорит на  немецком, не играет на виолончели.

5.Жанна знает французский язык, но не играет на скрипке.

Кто на каком инструменте играет и какой иностранный язык знает?

2.Применение теории графов в различных сферах деятельности.

Чем больше я изучал теорию графов, тем больше поражался разнообразию применения этой теории.

Типичными графами на картах города являются схемы движения городского транспорта, изображения железных дорог, схемы авиалиний, которые часто вывешивается в аэропортах. Графом является и система улиц города. Его вершины – площади и перекрестки, а ребра – улицы. Графы есть и на картах звездного неба.

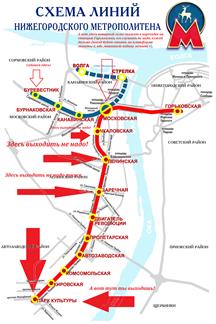
С помощью графов часто упрощается решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии. Помогают графы в решении математических и экономических задач.

Теория графов сейчас одна из самых развиваемых частей математики, так как современная жизнь требует появление новых профессий.  Одна из них – специалист по логистике. Менеджер по логистике занимается доставкой товаров, грузов, планирует транспортные маршруты, рассчитывает стоимость перевозок, организует хранение товаров, грузов и т.д. Одна из главных задач специалиста по логистике - анализ ситуации, поэтому он должен уметь хорошо считать, владеть теорией графов.

Инженер чертит схемы электрических цепей.

Химик рисует структурные формулы, чтобы показать, как в сложной молекуле с помощью валентных связей соединяются друг с другом атомы.

Историк прослеживает родословные связи по генеалогическому дереву.

Военачальник наносит на карту сеть коммуникаций, по которым из тыла к передовым частям доставляется подкрепление.

Социолог по сложнейшей диаграмме показывает, как подчиняются друг другу различные отделы одной огромной корпораций.

  Графы применяются в различных отраслях науки. В последние десятилетия теория графов находит все новые области применения (физика, химия, генетика, психология, социология, экономика, лингвистика, электроника, теория планирования и управления). Именно запросы практики способствуют интенсивному развитию теории графов.

2.1.Графы и история.

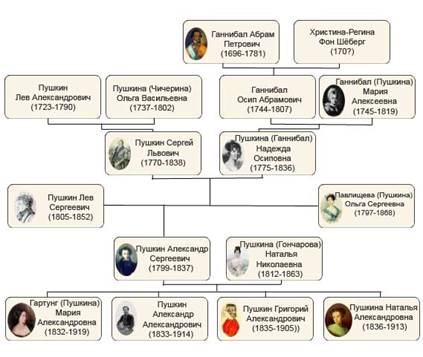
Использует графы и история. Например, в генеалогическом дереве, вершины – члены рода, а связывающие их отрезки – отношения родственности.

Генеалогическое дерево А.С. Пушкина.

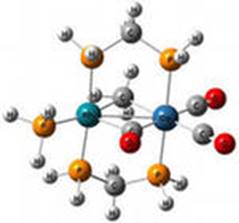
2.2.Графы и химия.

Теория графов в химии применяется для решения различных теоретических и прикладных задач. Применение графов теории базируется на построении и анализе различных классов химических и химико-технологических графов, которые называются также топология, т.е. модели, учитывающие только характер связи вершин. Ребра и вершины этих графов отображают химические и химико-технологические понятия, явления, процессы или объекты и соответственно качественные и количественные взаимосвязи либо определенные отношения между ними.

При графическом изображении формул веществ указывается последовательность расположения атомов в молекуле с помощью, так называемых валентных штрихов (термин «валентный штрих» предложил в 1858 г. А. Купер для обозначения химических сил сцепления атомов), иначе называемых валентной чертой (каждая валентная черта, или валентный штрих, эквивалентны одной паре электронов в ковалентных соединениях или одному электрону, участвующему в образовании ионной связи).

Химические графы дают возможность прогнозировать химические превращения, пояснять сущность и систематизировать некоторые основные понятия химии.

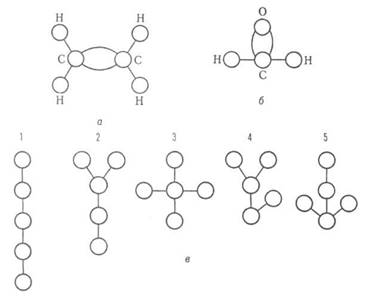
Молекулярные графы, применяемые в стереохимии и структурной топологии, химии кластеров, полимеров и др., представляют собой неориентированные графы, отображающие строение молекул. Вершины и ребра этих графов отвечают соответственно атомам и химическим связям между ними.

Молекулярные графы и деревья: а, б - мультиграфы  этилена и формальдегида; в-молекулы изомеров пентана.

4.3.Графы и физика

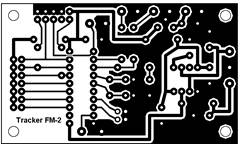
Еще недавно одной из наиболее сложных и утомительных задач для радиолюбителей было конструирование печатных схем.

Печатной схемой называют пластинку из какого-либо диэлектрика (изолирующего материала), на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы, их пересечение в других местах вызовет замыкание электрической цепи.

 В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами в указанных точках.

Изучая этот материал, я узнал области применения теории графов и сделал вывод, что этот раздел математики является одним из важнейших, который используется в нашей повседневной жизни часто незаметно для нас.

Заключение.

·        Чтобы найти ответ на  интересующую меня задачу, мне пришлось познакомиться с новым разделом математики «Теория графов», который не изучается в школьной программе, но облегчает решение многих задач,  я узнал много нового.

·        Изучая этот материал, я  овладел основными понятиями теории графов, узнал области применения теории графов.

·        Итак, для того чтобы научиться решать задачи, надо разобраться в том, что они собой представляют, как устроены, каковы инструменты, с помощью которых производится решение задач.

·        Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту.

·        Графовые задачи позволяют развивать логическое мышление. Они допускают изложение в занимательной форме, для их решения следует применить смекалку.

·        Я убедился, что графы достаточно широко применяются в экономике, управлении, технике.

·        В данной работе я рассмотрел задачи, которые решаются с помощью графов, и проанализировал их применение в различных сферах жизни.

·        Моя гипотеза подтвердилась – графы действительно широко используются в экономике, истории, химии, физике и т.д., а также в бытовых ситуациях.

·        Итак, я доказал практическую ценность графов, что и было целью данной работы.

Список литературы.

1.     Березина Л.Ю. Графы и их применение. Москва, «Просвещение», 1979.

2.     Галкин Е.В. Нестандартные задачи по математике. Задачи логического характера. Книга для учащихся 5-11 классов. “Просвещение” – “Учебная литература” Москва 1996 Энциклопедический словарь юного математика.  Москва, Педагогика, 1985г.

3.     Засенок В.П. Графы в математике и в жизни/программа интеллектуального развития учащихся /выпуск 6./ Инновационно-образовательный центр-М. 1997года.

4.     Коннонова Е.Г. Математика. Подготовка к олимпиадам. 7-11 классы.

5.     Фарков А.В. Математические олимпиады.

Список онлайн-ресурсов.

1.     https://globallab.org/ru/project/cover/reshenie_zadatch_s_pomoshju_grafa.ru.html#.WgAagF27WUl

2.     https://ru.wikipedia.org/wiki/Граф_(математика)

Рецензия

на исследовательскую  работу

«Практическое применение графов»

Цыбульского Артема Николаевича,  ученика 8 класса

ЧОУ «Средней школы им. Н.И. Лобачевского»

           Для рецензирования была представлена исследовательская работа «Практическое применение графов».

В математике и смежных с ней дисциплинах существует класс задач, которые наиболее просто и понятно решаются с применением теории графов. Это замечательные математические объекты, применяя которые можно решать логические задачи. Также c применением графов можно решать различные головоломки и упрощать условия задач. 

Теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Графы буквально вездесущи. В виде графов можно, например, интерпретировать схемы дорог и электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей. За последние четыре десятилетия теория графов превратилась в один из наиболее бурно-  развивающихся разделов математики. Это вызвано запросами стремительно расширяющейся области приложений

Данная работа состоит из введения, теоретической части, исследовательской части, заключения, списка источников и литературы.

Во введении автор работы обозначил проблему, цели и задачи исследования.

 В теоретической части автор рассматривает понятие  графа и виды графов.

В исследовательской части Артем разбирает решение логических задач с помощью графов.

 По итогам каждого из разделов были сделаны выводы в соответствии с поставленной проблемой.

 В заключение заботы представлены источники, которые автор использовал при написании исследовательской работы.

     Работа заслуживает высокой оценки и может быть представлена на городских, всероссийских и международных конкурсах исследовательских работ учащихся.

Учитель математики                                                        Е.В.Лукьянова

Скачано с www.znanio.ru