
Задание № 8. Преобразование выражений
Вариант 1
1. Сумма углов правильного выпуклого многоугольника вычисляется по
формуле ![]() где n —
количество его углов. Пользуясь этой формулой, найдите n,
если
где n —
количество его углов. Пользуясь этой формулой, найдите n,
если ![]() = 15π.
= 15π.
2. Площадь треугольника ![]() можно
вычислить по формуле
можно
вычислить по формуле ![]() где a —
сторона треугольника, h — высота, проведенная к этой
стороне (в метрах). Пользуясь этой формулой, найдите сторону
где a —
сторона треугольника, h — высота, проведенная к этой
стороне (в метрах). Пользуясь этой формулой, найдите сторону ![]() если
площадь треугольника равна
если
площадь треугольника равна ![]() а высота
h равна 14 м.
а высота
h равна 14 м.
3. Энергия заряженного конденсатора W (в Дж)
вычисляется по формуле ![]() где C —
ёмкость конденсатора (в Ф), а U — разность потенциалов на
обкладках конденсатора (в В). Найдите W (в Дж), если
где C —
ёмкость конденсатора (в Ф), а U — разность потенциалов на
обкладках конденсатора (в В). Найдите W (в Дж), если ![]() Ф и U = 20 В.
Ф и U = 20 В.
4. Работа постоянного тока (в джоулях) вычисляется по формуле ![]() где U —
напряжение (в вольтах), R — сопротивление (в омах),
где U —
напряжение (в вольтах), R — сопротивление (в омах), ![]() —
время (в секундах). Пользуясь этой формулой, найдите A (в
джоулях), если
—
время (в секундах). Пользуясь этой формулой, найдите A (в
джоулях), если ![]() с,
с, ![]() В
и
В
и ![]() Ом.
Ом.
5. Теорему косинусов можно записать в виде ![]() где a, b и c —
стороны треугольника, а
где a, b и c —
стороны треугольника, а ![]() — угол между
сторонами a и
— угол между
сторонами a и ![]() Пользуясь этой формулой,
найдите величину
Пользуясь этой формулой,
найдите величину ![]() если
если ![]() и
и ![]()
6. Площадь четырёхугольника можно вычислить по формуле ![]() где
где ![]() и
и ![]() — длины диагоналей
четырёхугольника,
— длины диагоналей
четырёхугольника, ![]() — угол между
диагоналями. Пользуясь этой формулой, найдите длину диагонали
— угол между
диагоналями. Пользуясь этой формулой, найдите длину диагонали ![]() если
если ![]()
![]() а
а ![]()
7. Мощность постоянного тока (в ваттах) вычисляется по формуле ![]() где U —
напряжение (в вольтах), R — сопротивление (в омах). Пользуясь
этой формулой, найдите P (в ваттах), если R = 6 Ом
и U = 12 В.
где U —
напряжение (в вольтах), R — сопротивление (в омах). Пользуясь
этой формулой, найдите P (в ваттах), если R = 6 Ом
и U = 12 В.
8. Площадь трапеции вычисляется по формуле ![]() где a и b —
длины оснований трапеции, h — её высота. Пользуясь этой
формулой, найдите площадь S, если a = 4, b = 9
и h = 2.
где a и b —
длины оснований трапеции, h — её высота. Пользуясь этой
формулой, найдите площадь S, если a = 4, b = 9
и h = 2.
9. Площадь треугольника можно вычислить по формуле ![]() где a, b и c —
стороны треугольника, а R — радиус окружности, описанной
около этого треугольника. Пользуясь этой формулой, найдите площадь S,
если a = 4, b = 13, c = 15
и
где a, b и c —
стороны треугольника, а R — радиус окружности, описанной
около этого треугольника. Пользуясь этой формулой, найдите площадь S,
если a = 4, b = 13, c = 15
и ![]()
10. Мощность постоянного тока (в ваттах)
вычисляется по формуле ![]() где I —
сила тока (в амперах), R — сопротивление (в омах). Пользуясь
этой формулой, найдите P (в ваттах), если R = 5
Ом и I = 7 А.
где I —
сила тока (в амперах), R — сопротивление (в омах). Пользуясь
этой формулой, найдите P (в ваттах), если R = 5
Ом и I = 7 А.
Задание № 8. Преобразование выражений
Вариант 2
1. Длина биссектрисы ![]() проведенной к
стороне c треугольника со сторонами a, b и c,
вычисляется по формуле
проведенной к
стороне c треугольника со сторонами a, b и c,
вычисляется по формуле 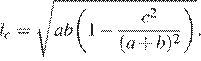 Треугольник
имеет стороны 9, 18 и 21. Найдите длину биссектрисы, проведённой к стороне
длины
Треугольник
имеет стороны 9, 18 и 21. Найдите длину биссектрисы, проведённой к стороне
длины ![]()
2. Чтобы перевести температуру из шкалы Цельсия в шкалу Фаренгейта, пользуются формулой tF = 1,8tC + 32, где tC — температура в градусах по шкале Цельсия, tF — температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Фаренгейта соответствуют 23 градусов по шкале Цельсия?
3. Энергия заряженного конденсатора W (в Дж)
вычисляется по формуле ![]() где C —
ёмкость конденсатора (в Ф), а q — заряд на одной обкладке
конденсатора (в Кл). Найдите W (в Дж), если
где C —
ёмкость конденсатора (в Ф), а q — заряд на одной обкладке
конденсатора (в Кл). Найдите W (в Дж), если ![]() Ф и q =
0,07 Кл.
Ф и q =
0,07 Кл.
4. Мощность постоянного тока (в ваттах) вычисляется по формуле ![]() где U ―
напряжение (в вольтах), R ― сопротивление (в омах).
Пользуясь этой формулой, найдите R (в омах), если P =
7 Вт и U = 14 В.
где U ―
напряжение (в вольтах), R ― сопротивление (в омах).
Пользуясь этой формулой, найдите R (в омах), если P =
7 Вт и U = 14 В.
5. Площадь треугольника можно вычислить по формуле ![]() где a, b и c —
стороны треугольника, а R — радиус окружности, описанной
около этого треугольника. Пользуясь этой формулой, найдите b,
если a = 12, с = 13, S = 30
и R =
где a, b и c —
стороны треугольника, а R — радиус окружности, описанной
около этого треугольника. Пользуясь этой формулой, найдите b,
если a = 12, с = 13, S = 30
и R = ![]()
6. Площадь параллелограмма ![]() можно
вычислить по формуле
можно
вычислить по формуле ![]() где
где ![]() —
стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь
параллелограмма, если его стороны 10 м и 12 м и
—
стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь
параллелограмма, если его стороны 10 м и 12 м и ![]()
7. Площадь прямоугольника равняется произведению половины квадрата
диагонали и синуса угла между диагоналями. Найдите площадь прямоугольника, если
длина диагонали равняется 5, а синус угла между диагоналями равен ![]()
8. Среднее квадратичное трёх чисел ![]() b и c вычисляется
по формуле
b и c вычисляется
по формуле 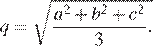 Найдите
среднее квадратичное чисел
Найдите
среднее квадратичное чисел ![]() и
и ![]()
9. Теорему косинусов можно записать в виде ![]() где a, b и c —
стороны треугольника, а
где a, b и c —
стороны треугольника, а ![]() — угол между
сторонами a и
— угол между
сторонами a и ![]() Пользуясь этой формулой,
найдите величину
Пользуясь этой формулой,
найдите величину ![]() если
если ![]() и
и ![]()
10. Известно, что ![]() Найдите
сумму
Найдите
сумму ![]()
Задание № 8. Преобразование выражений
Вариант 3
1. Площадь треугольника ![]() можно вычислить по формуле
можно вычислить по формуле ![]() где a —
сторона треугольника, h — высота, проведенная к этой
стороне (в метрах). Пользуясь этой формулой, найдите сторону
где a —
сторона треугольника, h — высота, проведенная к этой
стороне (в метрах). Пользуясь этой формулой, найдите сторону ![]() если площадь треугольника равна
если площадь треугольника равна ![]() а
высота h равна 14 м.
а
высота h равна 14 м.
2. Скорость камня (в м/с), падающего с высоты h (в
м), в момент удара о землю можно найти по формуле ![]() Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 62,5 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 62,5 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
3. Ускорение тела (в м / с2) при равномерном движении по окружности можно вычислить по формуле a = ω2R, где ω — угловая скорость вращения (в с−1), а R — радиус окружности (в метрах). Пользуясь этой формулой, найдите a (в м /с2), если R = 4 м и ω = 7 с−1.
4. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I2R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите R (в омах), если P = 15,75 Вт и I = 1,5 А.
5. Радиус описанной около треугольника окружности можно найти по
формуле ![]() где
a — сторона треугольника,
где
a — сторона треугольника, ![]() —
противолежащий этой стороне угол, а R — радиус описанной
около этого треугольника окружности. Пользуясь этой формулой, найдите
—
противолежащий этой стороне угол, а R — радиус описанной
около этого треугольника окружности. Пользуясь этой формулой, найдите ![]() если
если ![]() а
а ![]()
6. Энергия заряженного конденсатора W (в Дж) вычисляется по
формуле ![]() где C — ёмкость
конденсатора (в Ф), а q — заряд на одной обкладке
конденсатора (в Кл). Найдите W (в Дж), если C = 5 · 10−4 и q = 0,1
Кл.
где C — ёмкость
конденсатора (в Ф), а q — заряд на одной обкладке
конденсатора (в Кл). Найдите W (в Дж), если C = 5 · 10−4 и q = 0,1
Кл.
7. Количество теплоты (в джоулях), полученное однородным телом при
нагревании, вычисляется по формуле ![]() где c —
удельная теплоёмкость
где c —
удельная теплоёмкость ![]() m —
масса тела (в кг), t1 — начальная температура тела
(в кельвинах), а t2 — конечная температура тела (в
кельвинах). Пользуясь этой формулой, найдите Q если t2 = 608
К,
m —
масса тела (в кг), t1 — начальная температура тела
(в кельвинах), а t2 — конечная температура тела (в
кельвинах). Пользуясь этой формулой, найдите Q если t2 = 608
К, ![]() m = 3
кг и t1 = 603 К.
m = 3
кг и t1 = 603 К.
8. Работа постоянного тока (в джоулях) вычисляется по формуле ![]() где U —
напряжение (в вольтах), R — сопротивление (в омах),
где U —
напряжение (в вольтах), R — сопротивление (в омах), ![]() —
время (в секундах). Пользуясь этой формулой, найдите A (в
джоулях), если
—
время (в секундах). Пользуясь этой формулой, найдите A (в
джоулях), если ![]() с,
с, ![]() В
и
В
и ![]() Ом.
Ом.
9. Площадь треугольника можно вычислить по формуле ![]() где a, b и c —
стороны треугольника, а R — радиус окружности, описанной
около этого треугольника. Пользуясь этой формулой, найдите b,
если a = 9, с = 10, S = 36
и R =
где a, b и c —
стороны треугольника, а R — радиус окружности, описанной
около этого треугольника. Пользуясь этой формулой, найдите b,
если a = 9, с = 10, S = 36
и R = ![]()
10. Радиус окружности, описанной около
треугольника, можно вычислить по формуле ![]() где a —
сторона, а α — противолежащий ей угол треугольника. Пользуясь этой
формулой, найдите R, если a = 8 и
где a —
сторона, а α — противолежащий ей угол треугольника. Пользуясь этой
формулой, найдите R, если a = 8 и ![]()
Задание № 8. Преобразование выражений
Вариант 4
1. Площадь треугольника S со сторонами a, b, c можно
найти по формуле Герона ![]() где
где ![]() Найдите
площадь треугольника, если длины его сторон равны 25, 51, 74.
Найдите
площадь треугольника, если длины его сторон равны 25, 51, 74.
2. Теорему косинусов можно записать в виде ![]() где a, b и c —
стороны треугольника, а
где a, b и c —
стороны треугольника, а ![]() — угол между сторонами a и
— угол между сторонами a и ![]() Пользуясь этой формулой, найдите величину
Пользуясь этой формулой, найдите величину ![]() если
если ![]() и
и ![]()
3. В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях)
рассчитывается по формуле ![]() где t —
длительность поездки, выраженная в минутах
где t —
длительность поездки, выраженная в минутах ![]() Пользуясь
этой формулой, рассчитайте стоимость 15-минутной поездки. Ответ укажите в
рублях.
Пользуясь
этой формулой, рассчитайте стоимость 15-минутной поездки. Ответ укажите в
рублях.
4. Работа постоянного тока (в джоулях) вычисляется по формуле ![]() где U —
напряжение (в вольтах), R — сопротивление (в омах), t —
время (в секундах). Пользуясь этой формулой, найдите A (в
джоулях), если
где U —
напряжение (в вольтах), R — сопротивление (в омах), t —
время (в секундах). Пользуясь этой формулой, найдите A (в
джоулях), если ![]() с,
с, ![]() и
и ![]() Ом.
Ом.
5. Длину окружности l можно вычислить по
формуле ![]() где R —
радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус
окружности, если её длина равна 78 м. (Считать
где R —
радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус
окружности, если её длина равна 78 м. (Считать ![]() ).
).
6. Площадь трапеции вычисляется по формуле ![]() где a и b —
длины оснований трапеции, h — её высота. Пользуясь этой
формулой, найдите площадь S, если a = 4, b = 9
и h = 2.
где a и b —
длины оснований трапеции, h — её высота. Пользуясь этой
формулой, найдите площадь S, если a = 4, b = 9
и h = 2.
7. Второй закон Ньютона можно записать в виде F = ma , где F — сила (в ньютонах), действующая на тело, m — его масса (в килограммах), a — ускорение, с которым движется тело (в м/с2 ). Найдите m (в килограммах), если F = 296 Н и a = 37 м/с2.
8. Скорость камня (в м/с), падающего с высоты h (в
м), в момент удара о землю можно найти по формуле ![]() Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 10 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 10 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
9. Длина биссектрисы ![]() проведенной к
стороне c треугольника со сторонами a, b и c,
вычисляется по формуле
проведенной к
стороне c треугольника со сторонами a, b и c,
вычисляется по формуле 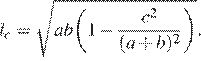 Треугольник
имеет стороны 9, 18 и 21. Найдите длину биссектрисы, проведённой к стороне
длины
Треугольник
имеет стороны 9, 18 и 21. Найдите длину биссектрисы, проведённой к стороне
длины ![]()
10. Найдите m из
равенства ![]() если
если ![]() и
и ![]()
Задание № 8. Преобразование выражений
Вариант 5
1. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой F = 1,8C + 32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует −1° по шкале Цельсия?
2. Теорему косинусов можно записать в виде ![]() где a, b и c —
стороны треугольника, а
где a, b и c —
стороны треугольника, а ![]() — угол между
сторонами a и
— угол между
сторонами a и ![]() Пользуясь этой формулой,
найдите величину
Пользуясь этой формулой,
найдите величину ![]() если
если ![]() и
и ![]()
3. В фирме «Эх, прокачу!» стоимость поездки на такси (в рублях)
рассчитывается по формуле ![]() где t —
длительность поездки, выраженная в минутах
где t —
длительность поездки, выраженная в минутах ![]() Пользуясь
этой формулой, рассчитайте стоимость 8-минутной поездки.
Пользуясь
этой формулой, рассчитайте стоимость 8-минутной поездки.
4. Найдите m из равенства ![]() если
если ![]() и
и ![]()
5. Найдите x из равенства ![]() если
если ![]() и
и ![]()
6. Второй закон Ньютона можно записать в виде F = ma , где F — сила (в ньютонах), действующая на тело, m — его масса (в килограммах), a — ускорение, с которым движется тело (в м/с2 ). Найдите m (в килограммах), если F = 319 Н и a = 29 м/с2.
7. Среднее геометрическое трёх чисел a, b и
c вычисляется по формуле ![]() Вычислите
среднее геометрическое чисел 4, 18, 81.
Вычислите
среднее геометрическое чисел 4, 18, 81.
8. Закон Гука можно записать в виде F = kx, где F — сила (в ньютонах), с которой сжимают пружину, x — абсолютное удлинение (сжатие) пружины (в метрах), а k — коэффициент упругости. Пользуясь этой формулой, найдите x (в метрах), если F = 38 Н и k = 2 Н/м.
9. Скорость камня (в м/с), падающего с высоты h (в
м), в момент удара о землю можно найти по формуле ![]() Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 10 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 10 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
10. Перевести температуру из шкалы Фаренгейта
в шкалу Цельсия позволяет формула ![]() где tC —
температура в градусах по шкале Цельсия, tF —
температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Цельсия
соответствует 50 градусов по шкале Фаренгейта?
где tC —
температура в градусах по шкале Цельсия, tF —
температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Цельсия
соответствует 50 градусов по шкале Фаренгейта?
Задание № 8. Преобразование выражений
Вариант 6
1.Зная длину своего шага, человек может приближённо подсчитать
пройденное им расстояние s по формуле ![]() где n —
число шагов, l — длина шага. Какое расстояние прошёл человек,
если
где n —
число шагов, l — длина шага. Какое расстояние прошёл человек,
если ![]() см,
см, ![]() ?
Ответ выразите в километрах.
?
Ответ выразите в километрах.
2. Площадь треугольника можно вычислить по формуле ![]() где a, b и c —
стороны треугольника, а R — радиус окружности, описанной
около этого треугольника. Пользуясь этой формулой, найдите площадь S,
если a = 10, b = 9, c = 17
и
где a, b и c —
стороны треугольника, а R — радиус окружности, описанной
около этого треугольника. Пользуясь этой формулой, найдите площадь S,
если a = 10, b = 9, c = 17
и ![]()
3. Площадь параллелограмма ![]() можно
вычислить по формуле
можно
вычислить по формуле ![]() где
где ![]() —
стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь
параллелограмма, если его стороны 10 м и 12 м и
—
стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь
параллелограмма, если его стороны 10 м и 12 м и ![]()
4. Известно, что ![]() Найдите
сумму
Найдите
сумму ![]()
5. Работа постоянного тока (в джоулях) вычисляется по формуле A = I2Rt, где I — сила тока (в амперах), R — сопротивление (в омах), t — время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 2 с, I = 6 А и R = 5 Ом.
6. Скорость камня (в м/с), падающего с высоты h (в
м), в момент удара о землю можно найти по формуле ![]() Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 62,5 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 62,5 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
7. Найдите S из равенства ![]() если v0 =
6, t = 2, a = −2.
если v0 =
6, t = 2, a = −2.
8. Потенциальная энергия тела (в джоулях) в поле тяготения Земли
вблизи её поверхности вычисляется по формуле ![]() где m —
масса тела (в килограммах), g — ускорение свободного падения
(в м/с2 ), а h — высота (в метрах), на
которой находится это тело, относительно поверхности. Пользуясь этой формулой,
найдите m (в килограммах), если g = 9,8 м/с2, h =
5 м, а E = 196 Дж.
где m —
масса тела (в килограммах), g — ускорение свободного падения
(в м/с2 ), а h — высота (в метрах), на
которой находится это тело, относительно поверхности. Пользуясь этой формулой,
найдите m (в килограммах), если g = 9,8 м/с2, h =
5 м, а E = 196 Дж.
9. Площадь ромба ![]() можно
вычислить по формуле
можно
вычислить по формуле ![]() где
где
![]() — диагонали
ромба (в метрах). Пользуясь этой формулой, найдите диагональ
— диагонали
ромба (в метрах). Пользуясь этой формулой, найдите диагональ ![]() если диагональ
если диагональ ![]() равна 30 м, а площадь
ромба 120 м2.
равна 30 м, а площадь
ромба 120 м2.
10. Теорему косинусов можно записать в
виде ![]() где a, b и c —
стороны треугольника, а γ — угол между сторонами a и b.
Пользуясь этой формулой, найдите величину cos γ , если a =
7, b =10 и c = 11.
где a, b и c —
стороны треугольника, а γ — угол между сторонами a и b.
Пользуясь этой формулой, найдите величину cos γ , если a =
7, b =10 и c = 11.
Задание № 8. Преобразование выражений
Вариант 7
1. Мощность постоянного тока (в ваттах) вычисляется по формуле ![]() где U —
напряжение (в вольтах), R — сопротивление (в омах). Пользуясь
этой формулой, найдите P (в ваттах), если R = 6 Ом
и U = 12 В.
где U —
напряжение (в вольтах), R — сопротивление (в омах). Пользуясь
этой формулой, найдите P (в ваттах), если R = 6 Ом
и U = 12 В.
2.Работа постоянного тока (в джоулях) вычисляется по формуле A = I2Rt, где I — сила тока (в амперах), R — сопротивление (в омах), t — время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 3 с, I = 5 А и R = 10 Ом.
3. Скорость камня (в м/с), падающего с высоты h (в
м), в момент удара о землю можно найти по формуле ![]() Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 0,4 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 0,4 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
4. Сумма углов правильного выпуклого многоугольника вычисляется по
формуле ![]() где n — количество его
углов. Пользуясь этой формулой, найдите n, если
где n — количество его
углов. Пользуясь этой формулой, найдите n, если ![]() = 15π.
= 15π.
5. Площадь треугольника со сторонами a, b, c можно
найти по формуле Герона ![]() где
где ![]() Найдите
площадь треугольника, если длины его сторон равны 7, 15, 20.
Найдите
площадь треугольника, если длины его сторон равны 7, 15, 20.
6. Зная длину своего шага, человек может приближённо подсчитать
пройденное им расстояние s по формуле ![]() где n —
число шагов, l — длина шага. Какое расстояние прошёл человек,
если
где n —
число шагов, l — длина шага. Какое расстояние прошёл человек,
если ![]() см,
см, ![]() ? Ответ выразите в
километрах.
? Ответ выразите в
километрах.
7. Площадь треугольника вычисляется по формуле ![]() где b и с —
две стороны треугольника, а
где b и с —
две стороны треугольника, а ![]() — угол между ними.
Пользуясь этой формулой, найдите величину
— угол между ними.
Пользуясь этой формулой, найдите величину ![]() если b =
5, с = 8 и S = 2.
если b =
5, с = 8 и S = 2.
8. Найдите S из равенства ![]() если v0 =
6, t = 2, a = −2.
если v0 =
6, t = 2, a = −2.
9. Площадь трапеции вычисляется по формуле ![]() где a и b —
длины оснований трапеции, h — её высота. Пользуясь этой
формулой, найдите площадь S, если a = 4, b = 9
и h = 2.
где a и b —
длины оснований трапеции, h — её высота. Пользуясь этой
формулой, найдите площадь S, если a = 4, b = 9
и h = 2.
10. Длину биссектрисы треугольника,
проведённой к стороне a, можно вычислить по формуле ![]() Вычислите
Вычислите
![]() если
если
![]()
Задание № 8. Преобразование выражений
Вариант 8
1. Среднее квадратичное трёх чисел ![]() и c вычисляется
по формуле
и c вычисляется
по формуле 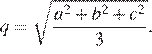 Найдите
среднее квадратичное чисел
Найдите
среднее квадратичное чисел ![]()
![]() и
и ![]()
2. Среднее геометрическое трёх чисел ![]() b и c вычисляется
по формуле
b и c вычисляется
по формуле ![]() Вычислите среднее геометрическое чисел
Вычислите среднее геометрическое чисел ![]()
![]() и
и ![]()
3. Закон Гука можно записать в виде ![]() где F -
сила (в ньютонах), с которой растягивают пружину, x —
абсолютное удлинение пружины (в метрах), а k — коэффициент
упругости. Пользуясь этой формулой, найдите x (в метрах),
если
где F -
сила (в ньютонах), с которой растягивают пружину, x —
абсолютное удлинение пружины (в метрах), а k — коэффициент
упругости. Пользуясь этой формулой, найдите x (в метрах),
если ![]() Н и
Н и ![]() Н/м.
Н/м.
4. Площадь треугольника можно вычислить по формуле ![]() где a, b и c —
стороны треугольника, а R — радиус окружности, описанной
около этого треугольника. Пользуясь этой формулой, найдите площадь S,
если a = 4, b = 13, c = 15
и
где a, b и c —
стороны треугольника, а R — радиус окружности, описанной
около этого треугольника. Пользуясь этой формулой, найдите площадь S,
если a = 4, b = 13, c = 15
и ![]()
5. Чтобы перевести температуру из шкалы Цельсия в шкалу Фаренгейта, пользуются формулой tF = 1,8tC + 32, где tC — температура в градусах по шкале Цельсия, tF — температура в градусах по шкале Фаренгейта. Скольким градусам по шкале Фаренгейта соответствуют 23 градусов по шкале Цельсия?
6. Длину окружности l можно вычислить по
формуле ![]() где R — радиус окружности (в метрах).
Пользуясь этой формулой, найдите радиус окружности, если её длина
равна 78 м. (Считать
где R — радиус окружности (в метрах).
Пользуясь этой формулой, найдите радиус окружности, если её длина
равна 78 м. (Считать ![]() ).
).
7. Зная длину своего шага, человек может приближённо подсчитать
пройденное им расстояние s по формуле ![]() где n —
число шагов, l — длина шага. Какое расстояние прошёл человек,
если
где n —
число шагов, l — длина шага. Какое расстояние прошёл человек,
если ![]() см,
см, ![]() ? Ответ выразите в
километрах.
? Ответ выразите в
километрах.
8. Скорость камня (в м/с), падающего с высоты h (в
м), в момент удара о землю можно найти по формуле ![]() Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 10 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
Найдите
скорость (в м/с), с которой ударится о землю камень, падающий с высоты 10 м.
Считайте, что ускорение свободного падения g равно 9,8 м/с2 .
9. Второй закон Ньютона можно записать в виде F = ma , где F — сила (в ньютонах), действующая на тело, m — его масса (в килограммах), a — ускорение, с которым движется тело (в м/с2 ). Найдите m (в килограммах), если F = 195 Н и a = 39 м/с2.
10. Количество теплоты (в джоулях), полученное
однородным телом при нагревании, вычисляется по формуле ![]() где c —
удельная теплоёмкость
где c —
удельная теплоёмкость ![]() m —
масса тела (в кг), t1 — начальная температура тела
(в кельвинах), а t2 — конечная температура тела (в
кельвинах). Пользуясь этой формулой, найдите Q если t2 = 608
К,
m —
масса тела (в кг), t1 — начальная температура тела
(в кельвинах), а t2 — конечная температура тела (в
кельвинах). Пользуясь этой формулой, найдите Q если t2 = 608
К, ![]() m = 3
кг и t1 = 603 К.
m = 3
кг и t1 = 603 К.
Задание № 8. Преобразование выражений
Вариант 9
1. Площадь трапеции вычисляется по формуле ![]() где a и b —
длины оснований трапеции, h — её высота. Пользуясь этой
формулой, найдите площадь S, если a = 4, b = 9
и h = 2.
где a и b —
длины оснований трапеции, h — её высота. Пользуясь этой
формулой, найдите площадь S, если a = 4, b = 9
и h = 2.
2. Радиус окружности, описанной около треугольника, можно вычислить
по формуле ![]() где a — сторона,
а
где a — сторона,
а ![]() — противолежащий ей угол треугольника. Пользуясь
этой формулой, найдите радиус R, если a = 10
и
— противолежащий ей угол треугольника. Пользуясь
этой формулой, найдите радиус R, если a = 10
и ![]()
3. Длина биссектрисы ![]() проведенной к
стороне c треугольника со сторонами a, b и c,
вычисляется по формуле
проведенной к
стороне c треугольника со сторонами a, b и c,
вычисляется по формуле 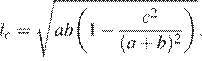 Треугольник
имеет стороны 9, 18 и 21. Найдите длину биссектрисы, проведённой к стороне
длины
Треугольник
имеет стороны 9, 18 и 21. Найдите длину биссектрисы, проведённой к стороне
длины ![]()
4. Площадь поверхности прямоугольного параллелепипеда с рёбрами ![]() и c можно
найти по формуле
и c можно
найти по формуле ![]() Найдите
площадь поверхности прямоугольного параллелепипеда с рёбрами
Найдите
площадь поверхности прямоугольного параллелепипеда с рёбрами ![]() и
и ![]()
5. Ускорение тела (в м/с2) при равномерном движении по
окружности можно вычислить по формуле ![]() где ω ―
угловая скорость вращения (в с−1 ), а R ―
радиус окружности (в метрах). Пользуясь этой формулой, найдите a (в
м/с2), если R = 40 дм, а
где ω ―
угловая скорость вращения (в с−1 ), а R ―
радиус окружности (в метрах). Пользуясь этой формулой, найдите a (в
м/с2), если R = 40 дм, а ![]()
6. Среднее квадратичное трёх чисел ![]() b и c вычисляется
по формуле
b и c вычисляется
по формуле 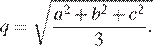 Найдите
среднее квадратичное чисел
Найдите
среднее квадратичное чисел ![]() и
и ![]()
7. Энергия заряженного конденсатора W (в Дж)
вычисляется по формуле ![]() где C —
ёмкость конденсатора (в Ф), а U — разность потенциалов на
обкладках конденсатора (в В). Найдите W (в Дж), если
где C —
ёмкость конденсатора (в Ф), а U — разность потенциалов на
обкладках конденсатора (в В). Найдите W (в Дж), если ![]() Ф и U = 16 В.
Ф и U = 16 В.
8. Радиус вписанной в прямоугольный треугольник окружности можно
найти по формуле ![]() где
a и b — катеты, а c —
гипотенуза треугольника. Пользуясь этой формулой, найдите b, если
где
a и b — катеты, а c —
гипотенуза треугольника. Пользуясь этой формулой, найдите b, если
![]() и
и ![]()
9. Среднее гармоническое трёх чисел ![]() и c вычисляется
по формуле
и c вычисляется
по формуле 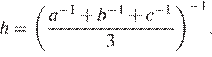 Найдите
среднее гармоническое чисел
Найдите
среднее гармоническое чисел ![]() и
и ![]()
10. Работа постоянного тока (в джоулях) вычисляется по формуле A = I2Rt, где I — сила тока (в амперах), R — сопротивление (в омах), t — время (в секундах). Пользуясь этой формулой, найдите A (в джоулях), если t = 5 с, I = 2 А и R = 13 Ом.
|
Ключ № 1
|
Ключ № 2
|
Ключ № 3
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ключ № 4
|
Ключ № 5
|
Ключ № 6
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ключ № 7
|
Ключ № 8
|
Ключ № 9
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.