Добавить материал

и получить 10 документов
и свидетельство автора

Грабарь Олеся Александровна

Тригонометрический круг

docx
31.08.2022

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

Тригонометрический круг.docx

Тригонометрический круг

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

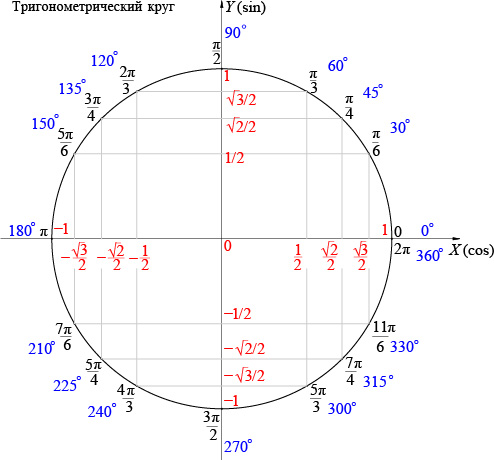
· Тригонометрический круг

Вот что мы видим на этом рисунке:

1. Перевод градусов в радианы и наоборот. Полный круг содержит 360 градусов, или $2 \pi$ радиан.

2. Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .

3. И синус, и косинус принимают значения от -1 до 1.

4. Значение тангенса угла $\alpha$ тоже легко найти — поделив $\sin \alpha$ на $\cos \alpha$ . А чтобы найти, котангенс — наоборот, косинус делим на синус.

5. Знаки синуса, косинуса, тангенса и котангенса.

6. Синус — функция нечётная, косинус — чётная.

7. Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен $2 \pi$ .

А теперь подробно о тригонометрическом круге:

Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

Полный круг — 360 градусов.
Точка с координатами $\left( 1;0 \right)$ соответствует углу ноль градусов. Точка с координатами $\left( -1;0 \right)$ отвечает углу в $180^{\circ}$ , точка с координатами $\left( 0;1 \right)$ — углу в $90^{\circ}$ . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу $\alpha$ .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу $\alpha$ .

Например:

$cos\mkern 2mu 60^{\circ}=\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle 2}$ ;

$cos\mkern 2mu 0^{\circ}=1$ ;
$sin\mkern 2mu 45^{\circ}=\genfrac{}{}{}{0}{\displaystyle \sqrt{2}}{\displaystyle 2}$ ;
$sin\mkern 2mu 240^{\circ}=-\genfrac{}{}{}{0}{\displaystyle \sqrt{3}}{\displaystyle 2}$

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса $\left( x \right)$ , синус — ордината $\left( y \right)$ . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

$-1\leqslant cos\mkern 2mu\alpha \leqslant 1$ ,
$-1\leqslant sin\mkern 2mu\alpha \leqslant 1$ .

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

$cos^2\mkern 2mu\alpha+sin^2\mkern 2mu\alpha=1$

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу $\alpha$ , смотрим, положительны или отрицательны ее координаты по (это косинус угла $\alpha$ ) и по (это синус угла $\alpha$ ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует $2 \pi$ радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол $-30^{\circ}$ — это угол величиной в $30^{\circ}$ , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

$cos\mkern 2mu\left( -\alpha \right)=cos\mkern 2mu\alpha$ ,
$sin\mkern 2mu\left( -\alpha \right)=-sin\mkern 2mu\alpha$ .

Углы могут быть и больше градусов. Например, угол $732^{\circ}$ — это два полных оборота по часовой стрелке и еще $12^{\circ}$ . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через $360^{\circ}$ . То есть:

$cos\mkern 2mu\left( \alpha +360^{\circ}\cdot n \right)=cos\mkern 2mu\alpha$ ,
$sin\mkern 2mu\left( \alpha +360^{\circ}\cdot n \right)=sin\mkern 2mu\alpha$ ,

где — целое число. То же самое можно записать в радианах:

$cos\mkern 2mu\left( \alpha +2\pi n \right)=cos\mkern 2mu\alpha$ ,
$sin\mkern 2mu\left( \alpha +2\pi n \right)=sin\mkern 2mu\alpha$ .

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

$tg\mkern 2mu\alpha=\genfrac{}{}{}{0}{\displaystyle sin\mkern 2mu\alpha}{\displaystyle cos\mkern 2mu\alpha}$ ,

$ctg\mkern 2mu\alpha=\genfrac{}{}{}{0}{\displaystyle cos\mkern 2mu\alpha}{\displaystyle sin\mkern 2mu\alpha}$ .

В результате получим следующую таблицу.

$\varphi$	0	$\genfrac{}{}{}{0}{\displaystyle \pi}{\displaystyle 6}$	$\genfrac{}{}{}{0}{\displaystyle \pi}{\displaystyle 4}$	$\genfrac{}{}{}{0}{\displaystyle \pi}{\displaystyle 3}$	$\genfrac{}{}{}{0}{\displaystyle \pi}{\displaystyle 2}$	$\genfrac{}{}{}{0}{\displaystyle 2 \pi}{\displaystyle 3}$	$\genfrac{}{}{}{0}{\displaystyle 3 \pi}{\displaystyle 4}$	$\genfrac{}{}{}{0}{\displaystyle 5 \pi}{\displaystyle 6}$	$\pi$
$tg\mkern 2mu\varphi$	0	$\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle \sqrt{3}}$		$\sqrt{3}$	не существует	$-\sqrt{3}$		$-\frac{\displaystyle 1}{\displaystyle \sqrt{3}}$	0
$ctg\mkern 2mu\varphi$	не существует	$\sqrt{3}$		$\genfrac{}{}{}{0}{\displaystyle 1}{\displaystyle \sqrt{3}}$	0	$-\frac{\displaystyle 1}{\displaystyle \sqrt{3}}$		$-\sqrt{3}$	не существует

Тригонометрический круг Тригонометрический круг — это самый простой способ начать осваивать тригонометрию

Каждому углу от нуля до градусов соответствует точка на единичной окружности

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также